道砟颗粒二维廓形对破碎的影响研究

周陶勇，夏建军，许 平

(昆明理工大学 机电工程学院，云南 昆明 650500)

0 引言

有砟道床作为有砟轨道的重要基础，由一定级配的碎石组成，具有排水性好、承载能力强、适应性好等特点，发挥着减振降噪、分散列车荷载的作用。道砟作为构成有砟道床的重要部分，其发生破碎、粉化现象会引起有砟道床一系列的病害，导致道床维护周期缩短、维护成本增加，影响列车行车安全及乘客舒适性。

道砟破碎的研究主要集中在物理试验[1-4]以及离散元数值模拟[5-7]，道砟形态特征的研究主要是形状、棱角、纹理的量化以及三维模型的重构[8-9]。由此可见，以往的研究是分别对道砟的形态特征和破碎进行研究，但实际上道砟的不规则形状对自身破碎也有着不可忽视的影响[10-11]。因此准确探究道砟形态特征对破碎的影响，对降低有砟道床维护成本具有重要意义。

1 研究样本筛选

高速有砟铁路因其速度快、频率高、循环荷载次数多等因素，使得碎石道砟容易破碎、粉化，从而引起道床的沉降、板结、翻浆冒泥等病害。因此以高速铁路特级碎石道砟为研究对象，特级碎石大致共分为5个级配[12]，具体参数见表1。

表1 特级碎石道砟粒径级配Tab.1 Super ballast particle gradation

将粒径在50 mm与63 mm之间的道砟颗粒称为63 mm道砟，其他范围以此类推。利用振动筛分装置筛分出一定数量的5种粒径的道砟颗粒，振动筛分装置如图1(a)所示；然后从筛分好的道砟颗粒中选择150个各种形状的道砟颗粒作为研究样本，如图1(b)所示；以5种粒径为1个分组并进行编号，其中编号1-1表示第1组第1个颗粒，如图1(c)所示。

图1 五种粒径的道砟颗粒Fig.1 Ballast particles with 5 particle sizes

2 颗粒量化方法

2.1 图像采集与处理

道砟具有不规则的几何形态，国内外学者主要从道砟颗粒宏观尺寸、中观棱角以及微观纹理等方面进行研究。根据伊利诺伊大学Rao等[13]学者的研究，3个正交方向的视图便可以对颗粒宏观尺寸和中观棱角进行测量。

近年来，数字图像处理技术(Digital Image Processing，DIP)由于其操作简单，分析结果易于存储等特点而被广泛用于粗集料颗粒形态特征的定量分析[14-16]。获取颗粒几何图像时，通常采用数码相机、激光扫描仪或者CT等设备；相较于激光扫描仪和CT设备，数码相机的技术难度及成本都较低而被广泛用于图像采集。因此采用高分辨率的相机采集颗粒3个正交方向的图像，然后结合图像处理软件ImageJ对颗粒3个正交图像进行分割和测量。

2.2 形态特征量化指标

2.2.1 等效椭圆

等效椭圆也称为拟合椭圆，其兼顾了圆形和矩形的优点，能够较好拟合颗粒的边界。等效椭圆是根据道砟集料颗粒边界制作生成的，主要有3个参数即长轴、短轴以及方向角，如图2所示。在集料颗粒的二维特征量化时，主要涉及的还是长轴长度及短轴长度这两个参数的使用。

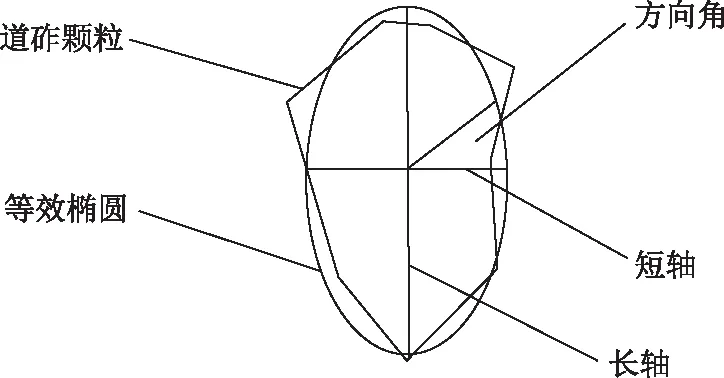
图2 道砟颗粒等效椭圆Fig.2 Equivalent ellipse of ballast particle

如果将颗粒的二维廓形图像当作是由连续的坐标点构成，那么可以采用数学方法求出颗粒的等效椭圆[17]，具体方式如下。

(1)首先在颗粒二维廓形上等距离取点，如图3所示。

图3 等距取点Fig.3 Equidistant point taking

(2)已知椭圆的一般方程为Ax2+Bxy+Cy2+Dx+Ey+F=0，(x,y)表示颗粒二维廓形上点的坐标，由方程可知只需求得6个未知系数便可得到等效椭圆方程，因此颗粒二维廓形上至少要取6个点，于是将各点的坐标带入椭圆的一般方程得：

(1)

化成矩阵形式为：

(2)

求解出A，B，C，D，E，F等6个系数便可以粗略画出颗粒的等效椭圆，若取点多于6个即n>6，拟合出来的椭圆则更精细。

2.2.2 扁平长细比(FER)

扁平长细比(Flat and Enlongated Ratio, FER)也称长宽比[18]或轴向系数[19]，主要是衡量颗粒形状扁平细长的一个指标，其被定义为颗粒等效椭圆长轴长度与短轴长度的比值。

(3)

式中，L为等效椭圆长轴长度；S为等效椭圆短轴长度。

将3个正交视图测量的等效椭圆长轴长度L和短轴长度S采用加权平均求解一个颗粒最终的扁平长细比值。

(4)

2.2.3 棱角参数(AI)

棱角参数(Angularity Index, AI)是衡量道砟颗粒廓形边界与等效椭圆边界偏差的参数, 其定义为颗粒周长P与等效椭圆周长C的比值，道砟颗粒的廓形边界突出起伏越多则颗粒周长P也越长，其比值也就越大表明道砟颗粒的廓形边界棱角越丰富。

(5)

采用加权平均求解道砟颗粒最终的棱角参数值。

(6)

2.3 岩石破碎分析

岩石破碎的经典理论主要是Rittinger的面积学说、Kick的体积学说以及Bond的裂缝学说，但3种主要理论学说存在着一定的局限性，无法说明岩石表面结构与粉碎之间的内在联系。

1984年Mandelbrot提出分形理论并应用于岩石破碎的研究，分形理论认为岩石颗粒表面具有自相似性的分形结构，Mandelbrot提出分形维数D来描述岩石颗粒的不规则程度，研究表明分形维数D值越大，岩石颗粒不规则程度越大。邓跃红等[20]对面积学说进行讨论和修正时推导出用分形维数D联系岩石破碎3大理论的公式：

(7)

式中，dE为单位粉碎能耗；A为岩石颗粒表面积；D为分形维数；x为颗粒粒度。

研究表明常见岩石颗粒的分形维数D在2～3之间，根据式(7)可知岩石颗粒分形维数D越大即外形不规则程度越大，岩石所需粉碎能耗就越大；岩石颗粒表面积越大所需粉碎能耗越小。由此可见，道砟作为自然界的岩石材料其表面结构的几何形态特征与自身的粉碎密切相关。

3 试验分析

3.1 加载试验

本研究采用液压加载装置进行试验，将道砟颗粒放置于加载装置与压力传感器之间，加载过程中始终保持加载端部与地面平行且匀速加载保证道砟颗粒垂直受力，如图4(a)所示。当道砟颗粒出现裂缝或破碎成多个碎块时停止加载，如图4(b)所示。

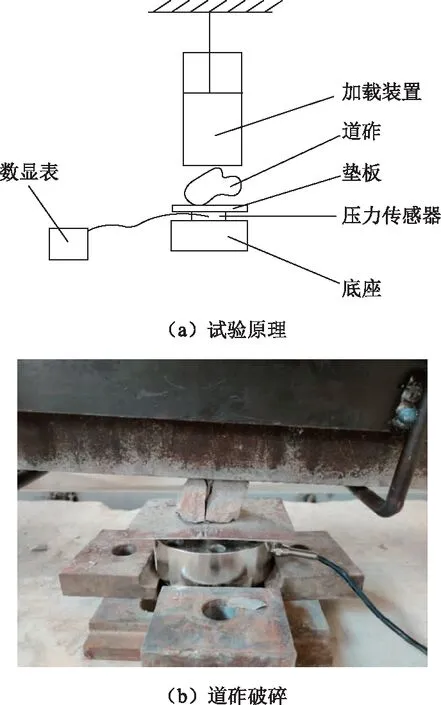
图4 道砟破碎试验Fig.4 Ballast crushing test

3.2 量化指标分析

压力F的数值通过数显表显示并记录，对道砟颗粒进行压碎试验，并对其结果进行处理得到各自的拟合图像和表达式。

扁平长细比与破碎压力线性拟合表达式为：

y=-11.907 49t+40.350 57。

(8)

由图5可以看出道砟破碎压力较为离散，主要原因是道砟内部微裂纹的初始数量不同。根据Griffith强度理论可知自然界材料内部存在着大量微裂纹，这些裂纹导致材料宏观上的断裂。拟合直线斜率为负值可得道砟破碎压力的变化趋势是随着FER值的增大而减小。原因是道砟FER值越大则道砟的外形越细长扁平，表面积也就越大。根据式(7)可知在粒度和分形维数确定的情况下道砟颗粒表面积越大破碎所需压力与能耗也就越小。

图5 道砟扁平长细比-压力Fig.5 Flat slenderness ratio vs. pressure of ballast

图6为5种粒径范围棱角参数与破碎压力的拟合直线，由拟合直线斜率为正值可得道砟颗粒破碎压力的变化趋势是随着AI值的增大而增大，主要是道砟AI值越大则尖锐棱角越丰富，道砟表面不规则程度增大，衡量道砟不规则程度的分形维数D增大，根据式(7)可知在粒度和表面积确定的情况下道砟不规则程度增大则粉碎所需压力与能耗也都将增大。除此以外，从上述FER值和AI值的破碎压力图像中可以得到在同一FER值和AI值下道砟破碎压力也并非完全相同，正如式(7)所示岩石颗粒的破碎还受到粒径的影响。

图6 道砟棱角参数-压力Fig.6 Angle parameter vs. pressure of Ballast

4 结论

本研究选取了部分道砟样本并利用数字图像处理技术对道砟形态特征进行量化，通过物理试验并结合岩石力学理论分析了道砟二维廓形对破碎的影响，得到以下结论：

(1)道砟形态特征对自身破碎的影响具体表现是道砟破碎时所受压力值随着扁平长细比值的增大而减小，主要是扁平长细比值越大道砟形状越扁平细长，道砟表面积也就越大破碎所需压力与能耗越小；破碎压力随着棱角参数值的增大而增大，主要是棱角参数值越大道砟棱角越丰富，道砟表面不规则程度越大破碎所需压力与能耗越大。

(2)在两个道砟颗粒扁平长细比值和棱角参数值分别相同的情况下，道砟破碎的压力也并非完全相同，说明道砟破碎除了受到形态特征的影响还受到粒径的影响。