Riesz空间分数阶Klein-Gordon-Zakharov方程的保能量格式
刘 莹, 孙建强, 孔嘉萌
(海南大学 理学院,海南 海口 570228)
著名的Zakharov方程是等离子体物理中Langmuir波传播研究中的偏微分方程模型[1]。Zakharov指出,任意足够强的Langmuir湍流是不稳定的,这种不稳定导致等离子体中低密度区域的发展,并在有限时间内崩塌。这些区域被称为洞穴,是长Langmuir振荡的能量耗散机制[2]。Zakharov系统推动了模型的进一步发展,为类似物理现象提供了更真实的描述,其中就包括Klein-Gordon-Zakharov系统[3-5]。直到今天,经典的Zakharov系统仍然被认为是描述高频Langmuir波和低频离子声波耦合的最佳系统之一,已经应用于描述浅水波和非线性光学中[6-7]。本研究考虑分数阶Klein-Gordon-Zakharov方程[8-13]
(1)

许多学者从理论或数值分析的角度研究分数阶偏微分方程,提出一些重要的解析方法来求解分数阶偏微分方程。同时,许多有效的数值方法,包括有限差分法、有限元法、有限体积法、谱方法等也被用来求解空间分数阶偏微分方程,并证明了它们的一致性、稳定性和收敛性[14-17]。Wang等[14]构造了一维Klein-Gordon-Zakharov系统的隐式保守有限差分格式和多对称拟谱方法。Bao等[11]提出Klein-Gordon-Zakharov系统的指数波积分傅里叶拟谱方法和一致精确的有限差分方法。本研究利用平均向量场方法构造了方程(1)的保能量格式。
1 傅里叶拟谱方法对Riesz空间分数阶导数的离散
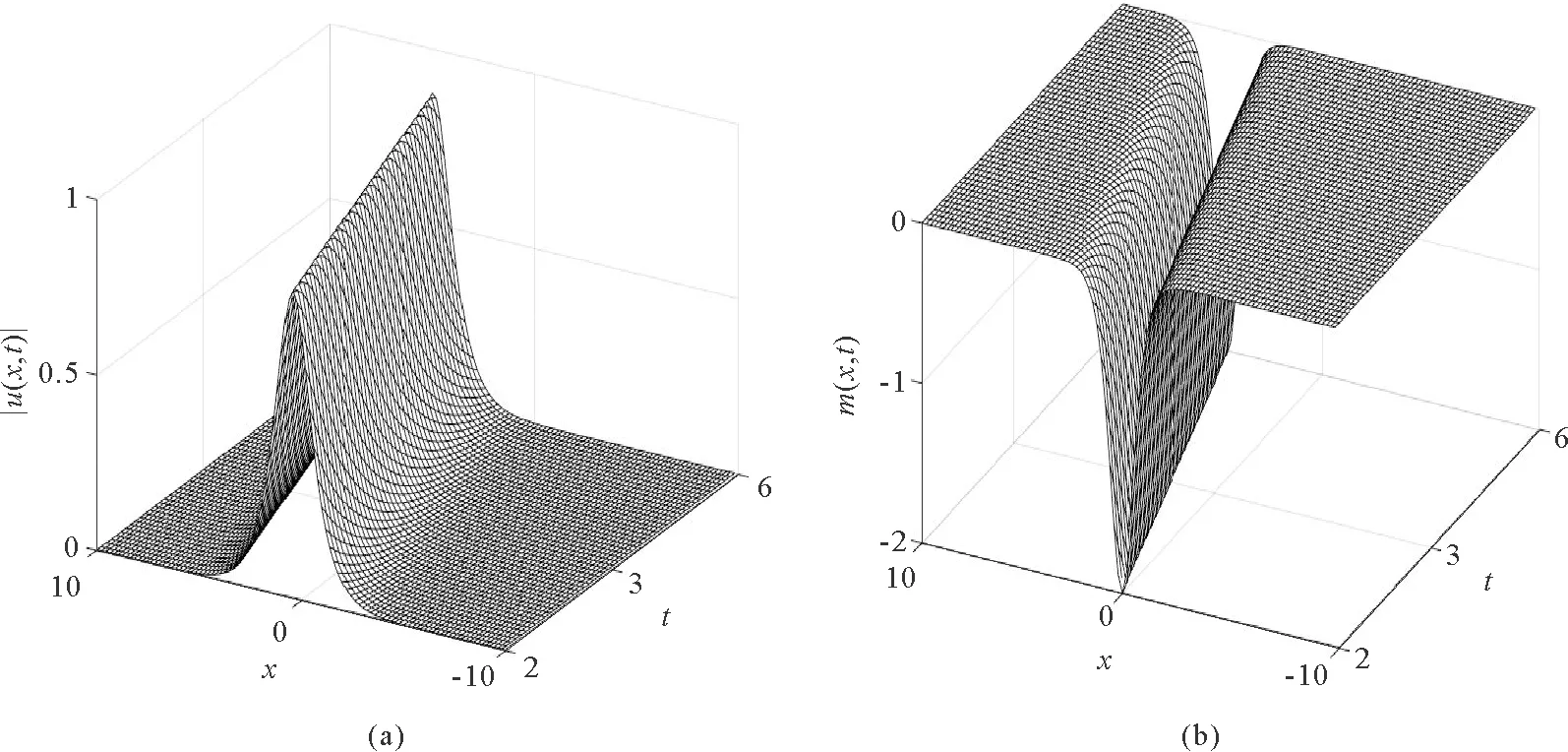
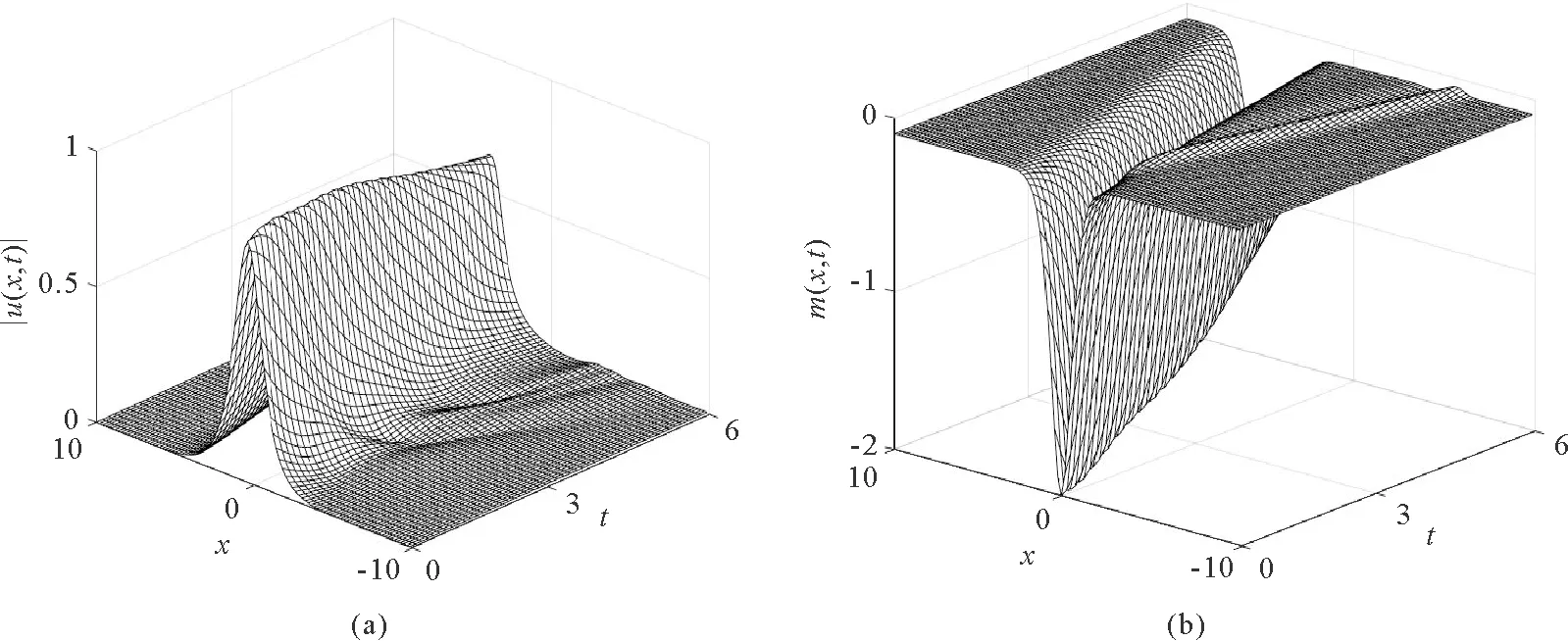
定义1当n-1<α (2) 引理1在无限区间(-∞ (3) 式中:n-1<α (4) 式中,F和F-1分别表示u(x,t)的傅里叶变换和傅里叶逆变换。因此,有: (5) 另外,在具有周期边界条件的有界区间Ω=(a,b)上,由傅里叶级数定义为: (6) 傅里叶系数为: (7) 由式(6)和式(7)可得: (8) (9) (10) 令w(x,t)=ut(x,t),-2qxx(x,t)=mt(x,t),则方程(1)等价于: (11) 方程组(11)可以被写成无限维哈密尔顿系统: (12) 式中:z=(u,m,w,q)T,I为2×2单位矩阵,哈密尔顿函数 (13) 用傅里叶拟谱方法对方程(12)在空间方向上进行离散。傅里叶拟谱方法的关键是对偏微分方程导数的离散。对于分数阶导数,相应谱矩阵为方程(10),对于二阶偏导数,相应的谱微分矩阵D2为: 从而得到方程(11)的半离散系统为: (14) 式中:j=0,…,N-1;Q=(q0,q1,…,qN-1)T。式(14)可表示为半离散哈密尔顿系统形式: (15) 式中:Z=(UT,MT,WT,QT)T,M=(m0,m1,…,mN-1)T,W=(w0,w1,…,wN-1)T,0和IN分别为N×N阶零矩阵和单位矩阵,相应的哈密尔顿函数为: (16) 在时间方向上利用二阶平均向量场方法离散哈密尔顿系统得[17]: (17) 式(17)等价于: (18) (19) (20) (21) 消去辅助变量w和q后,可得方程(1)的平均向量场格式: (22) (23) 分数阶Klein-Gordon-Zakharov方程的新格式(22)和(23)具有良好的稳定性和二阶收敛精度[20-21]。 为验证理论分析,利用得到的新格式(22)和(23)对Riesz空间分数阶非线性Klein-Gordon-Zakharov方程(1)进行数值模拟。定义相对能量误差为: (24) 考虑Riesz空间分数阶非线性Klein-Gordon-Zakharov方程在I=[-10,10]和长度T=6的时间周期上。取初始条件: (25) 图1是方程(1)孤立波在α=2.0和t∈[0,6]内的相互作用图,分别对应于孤立波|u(x,t)|和m(x,t)。 从图1可以发现,方程数值解的波形非常光滑,且运算结果与文献[8]一致,验证了所构造的新格式可以正确地数值模拟方程的解。图2是方程(1)孤立波在α=1.6和t∈[0,6]内的相互作用图。从图2可知,分数阶微分方程的孤立波振幅和波形在传输中发生了变形弯曲,表明分数阶Klein-Gordon-Zakharov微分方程中的孤立波很难稳定传播。图3是方程(1)在不同α时的能量图,从图中可以发现,α取不同值时方程能量都是一条直线,不随时间的变化而变化,运算结果与文献[8]一致,证明新格式能够精确地保持系统能量守恒。 图1 方程(1)孤立波在α=2.0和t∈[0,6]内的相互作用图 图2 方程(1)孤立波在α=1.6和t∈[0,6]内的相互作用图 图3 方程(1)在α取不同值时的能量图 本研究利用分数阶拉普拉斯算子与Riesz空间分数阶导数的关系以及傅里叶拟谱方法,对分数阶拉普拉斯算子的空间离散近似,从而得到傅里叶拟谱方法对Riesz空间分数阶导数的离散格式。在时间方向上利用平均向量场方法对哈密尔顿系统进行离散,构造出分数阶Klein-Gordon-Zakharov方程新的保能量格式,并利用得到的平均向量场格式对分数阶Klein-Gordon-Zakharov方程进行数值模拟。结果表明,新格式可以正确地模拟孤立波的演化行为,分数阶微分方程中的孤立波在传输中会发生弯曲和变形,同时方程取不同α值时的能量随时间的变化保持不变,验证了所构造的新格式能够精确地保持系统能量守恒。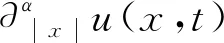

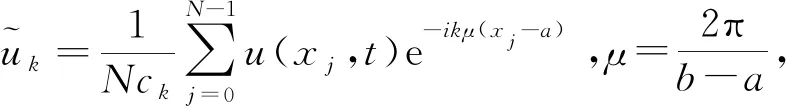
2 分数阶Klein-Gordon-Zakharov方程的保能量格式

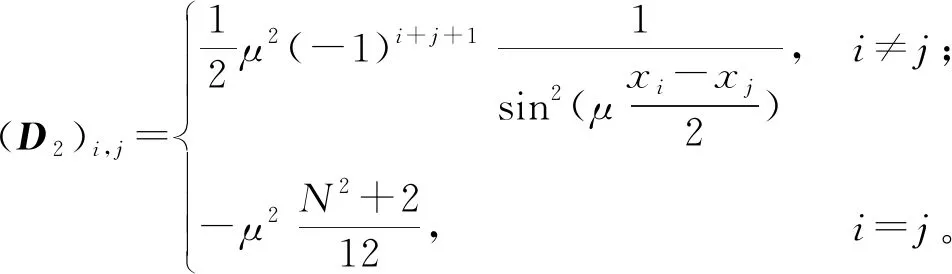
3 数值模拟

4 结论

