基于ADC 精度与AP 选择的去蜂窝系统能效均衡方法
丁青锋,徐梦引,石 辉,李怡浩,杨 倩
(华东交通大学电气与自动化工程学院,南昌 330013)
0 概述
在大规模多输入多输出(Multiple Input Multiple Output,MIMO)系统中,作为分布式MIMO 一个新的分支,去蜂窝大规模MIMO 系统通过大范围部署成百上千接入点(Access Point,AP)进行相互协作突破传统蜂窝网络小区边界及切换的瓶颈问题,缩短了AP 与用户间的平均距离,可在全区域内提供良好的信息传播条件[1-2]。为在全区域内获得良好的路径增益而大规模部署AP,其联合协作也会产生较大用户间干扰和不必要功耗,因此有必要针对每个用户进行AP 的有效选择[3]。
在去蜂窝大规模MIMO 系统中,AP 选择算法通过评估信道状态环境确定有效的AP 组合,在系统全局上有效减少用户间干扰和回程功耗的影响[4]。文献[5]提出以有效信道与干扰信道增益差值作为指标衡量信道干扰抑制能力的概念,由此用户可以选择一个信道干扰抑制能力最佳的AP,但由于选择的是单AP,无法保证信道硬化条件。在考虑选择多AP 情况下,针对上行传输,基于频谱效率的AP 选择算法以每个AP 服务后的频谱效率为筛选指标进行AP 选择[6],但该算法中筛选判定的阈值选取存在特殊性,适用性不高。在下行传输中,基于大尺度衰落的AP 选择算法[7]通过剔除大尺度衰落系数较小的AP 以减小回程功耗进而优化能量效率。另外,基于确定筛选数的AP 选择算法[8]通过降序排序AP 与用户端之间的估计信道的方差系数,筛选前半部分筛选数信道条件较好的AP 组合。为进一步优化频谱效率,基于信干噪比(Signal to Interference plus Noise Ratio,SINR)的AP 选择算法[9]以SINR 为排序指标,通过遍历每个AP 单独服务后的SINR 来移除影响较小的AP,进而确定有效的AP 组合来减小不必要功耗。基于K 均值++簇的AP 选择算法[10]通过使用群集机器学习来加速AP 分配,然而由于K值难以确定,优化问题中的非凸数据集难以收敛,且计算复杂度较高,并不适用于部署大规模AP 的去蜂窝MIMO 系统。
另外,为避免系统硬件成本和功率损耗随天线数呈指数级增长,配置合理精度模数转换器(Analog-to-Digital Converters,ADC)的射频链路是较为有效的方式[11]。低精度ADC 替代高精度ADC 以减小大规模天线带来的高功耗,并在增多AP 的基础上对量化干扰信号进行补偿,使频谱效率与能量效率达到平衡[12]。在考虑低精度ADC 量化基础上,利用基于人工搜索的量化精度算法可以得到最优的量化精度配置[13]。此外,在考虑低精度量化的射频链路中,利用Bussgang 分解来模拟量化效应,并给出解析解来寻找量化器的最佳步长以此获得一致的量化精度[14]。在此基础上,即使受有限回传功率的约束,配置较低精度ADC 并用简单的最大比合并(Maximum-Ratio Combining,MRC)解码技术,系统也能得到接近较优回传传输功率的性能[15]。
然而,在去蜂窝大规模MIMO 系统中对ADC 精度进行搜索的计算复杂性较高,为降低在全局搜索的复杂性,可通过选取不同精度ADC 并利用AP 选择实现频谱效率与能效的均衡,以此获取最优量化位数。目前,AP 选择算法普遍只局部考虑单个AP的服务质量和端与端之间的信道增益,未考虑联合AP 的服务质量的变化趋势和用户间干扰信道的影响。因此,为实现更好的系统能效均衡,本文提出一种基于ADC 精度选择和信号干扰差值的AP 选择的能效均衡方法。首先通过泊松过程确定用户数目及分布位置,在平均传输功率下,推导出配置低精度ADC 时频谱效率的闭式解。然后基于信道状态信息引入有效信号与干扰信号差值的概念,并将差值转换成比值作为AP 的排序指标。同时,分析排序后AP 逐层联合服务的频谱效率变化差值,直到差值小于阈值时停止筛选并确定所选AP 组合。最后通过ADC 精度和AP 选择联合优化,获取最优量化位数,以实现频谱效率与能效的均衡。
1 系统模型
考虑一个时分双工模式下的去蜂窝大规模MIMO 上行传输系统,发射端为K个单天线用户,接收端为L个AP。其中每个AP 配置M根天线,且每根天线连接着线性量化增益系数为α的ADC,并满足条件LM≫K。用户在一个平面区域A 中服从泊松分布,而所有AP 随机分布于A 中并通过回程网络连接到中央处理器(Central Processing Unit,CPU)。在时分双工模式下的上行传输系统中,考虑用户在同一时频资源下按每个相干间隔长度为τc进行数据采样,其中对τp个采样点进行导频训练,剩余部分用于上行的数据传输。
在上行训练过程中,满足τp≥K的条件下通过正交导频训练,利用最小均方误差的信道估计技术[16]得到第l个AP 与第k个用户间的信道估计向量及信道误差 向量分别为:

其中:nl~CN(0M×1,IM)为进行上行数据传输时第l个AP 处的加性高斯白噪声矢量[18]。然后,接收的信号经过ADC 进行量化。在运用加性量化噪声模型下,第l个AP 接收的 量化信号 矢量为:

其中:α是取决于ADC 量化位数b的线性增益,且满足条件0 <α≤1,其相关取值如表1 所示。当ADC 量化位数大于5 时,其信号通过ADC 量化后的失真系数即线性增益表示为α=1-表示经过ADC 量化后与无关的加性量化噪声,其协方差矩阵可以表示为

表1 不同ADC 量化位数下的失真系数Table 1 Distortion coefficients under different ADC quantization bits
利用MRC 算法对接收后的数据合并检测[21],则经过回传链路后CPU 接收的所有关于第k个用户的信号为:

2 能效均衡分析
2.1 频谱效率分析
在去蜂窝大规模MIMO 系统中,有效的信道增益一般在其均值上下浮动。基于AP 端获取的信道统计信息利用边界技术[22],在低精度ADC 量化下,式(5)可以表示为:
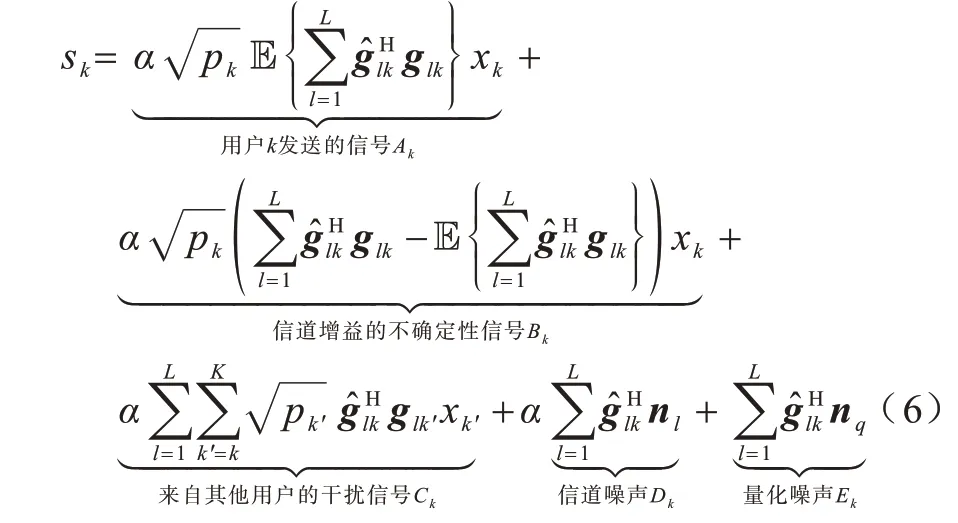
其中:右边第1 项为第k个用户发送到AP 的有效信号Ak;第2 项为信道增益不确定性信号Bk;第3 项为其他用户的干扰信号Ck;第4 项为信道噪声Dk;第5 项为量化噪声Ek且信号之间相互独立。
通过式(6)进一步求取频谱效率表达式。大规模MIMO 系统可利用大数定律得到以下定理[23]:
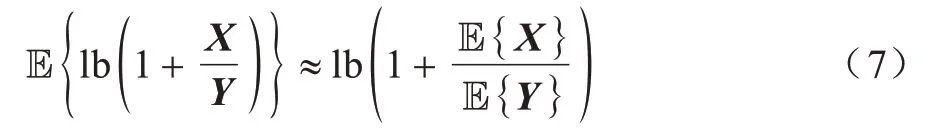
在去蜂窝大规模MIMO 系统中,系统总的上行频谱效率可以表示为:

其中:Rk为第k个用户的频谱效率。
第k个频谱效率表示为:

其中:rk为第k个用户的SINR。
第k个用户的SINR 可以表示为:

由于用户间信号相互独立,且满足信道硬化条件,式(10)的分母部分第2 项可以表示为:

同时,不同AP 下加性高斯白噪声也相互独立。因此,式(10)的分母部分第3 项可以表示为:
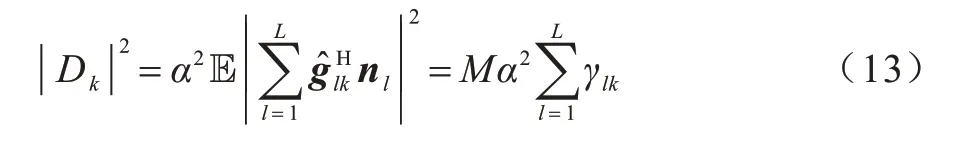
然后,由概率论相关知识,式(10)的分母部分第1 项可转化为:
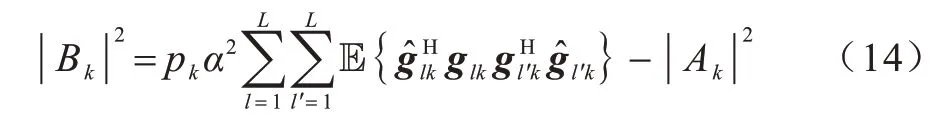
式(14)右边第1 项可以分解为:
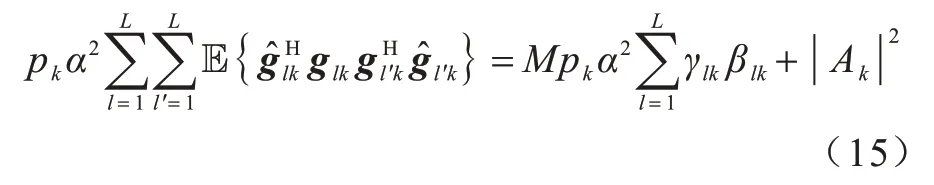
关于量化噪声的求解部分,量化噪声的协方差矩阵代入式(16)可得:

将式(11)~式(16)代入式(10)可得:
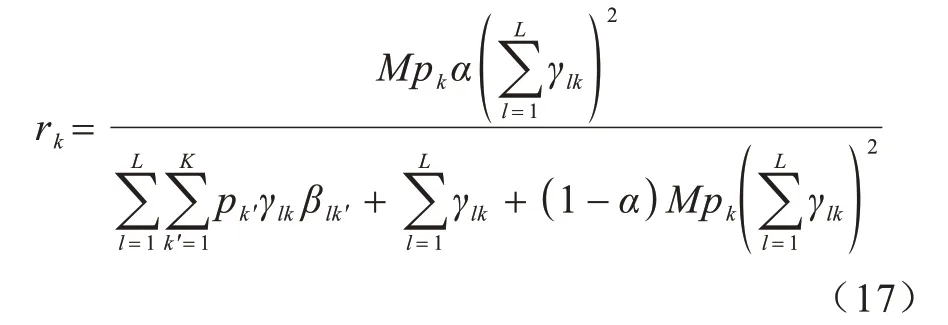
2.2 能量效率分析
上行传输系统功耗一般分为3 个部分:用户端消耗的功率PU,CPU 端消耗的回程功耗PB和AP 端链路功耗PA,其中AP 端的功耗包括电路固定功耗及ADC 的量化功耗[12,24],则总功耗表示为:

其中:μk为功率放大系数;W为带宽;fs及FOMW分别为量化环节的奈奎斯特采样率及瓦尔登品质因数;Ptc,k、Ptc,l、PAGC,l、P0,l分别为用户端电路功耗、AP 端每根天线的电路功耗、AGC 的固定功耗、流量控制的功耗系数,每条回程链路的固定功耗;cm是与量化精度有关的系数。在上行传输链路中,在ADC 精度确定的条件下,回程链路部分由流量控制的总功耗与服务用户的AP组合有关,其余功耗均为固定功耗;当ADC 量化位数变化时,AP 端关于ADC 量化的功耗也随之改变[12]。
基于上述公式,进一步求取总能量效率η,定义为总的频谱效率与功耗的占比,则有:

其中:R为去蜂窝MIMO 系统中总的频谱效率。
3 基于ADC 精度和AP 选择的能效均衡方法
假设用户分布服从泊松过程,考虑一个接收端的ADC 量化位数为b的上行传输系统。为使AP 端与用户端尽量实现有效连接并达到能效质量均衡,在用户端为平均传输功率,即在pk=pu条件下,本文提出一种基于ADC 精度和AP 选择的能效均衡方法。
3.1 多用户分布求解
由于用户在面积为S(A)的区域A 中分布的不确定性,考虑利用二维齐次泊松过程求解密度为λU(用户数/km2)的多用户分布。在该分布的求解中,用户数目K是满足=E(K)的泊松分布的随机变量,其期望可以表示为:

为贴近实际传输场景且便于分析,泊松变量K满足条件τp≥K和LM≫K;为生成均值为的泊松随机变量K,引入在0~1 内均匀分布的独立随机变量序列U1,U2,…,若满足式(21),则确定用户数量K及用户的位置分布。

通过泊松分布过程确定用户数目及位置,进一步利用信道估计技术确定用户与所有AP 之间的信道状态信息。设激活所有AP 时系统实际信道及估计信道的方差系数矩阵分别为B∈CL×K和γ∈CL×K。
3.2 信号干扰差值排序
在获取信道状态信息后,首先考虑将每个用户与所有AP 生成信道的大尺度衰落系数作为衡量指标对AP 进行排序,即将矩阵B按列进行降序排列。针对第k个用户,与所有AP 之间的大尺度衰落系数的排序结果为:

在不考虑干扰信道的影响下,一般默认βlk值越大,该条信道传播路径越好,但在同一AP 服务下的其他用户的信道增益可能会更大,使得该AP 下的用户间干扰较大。因此,只考虑自信道传输环境的排序方式并不能对AP 进行准确排序。
考虑同AP 下其他用户信道对有效用户信道环境的影响,可进一步优化排序方式。由式(17)可知,在ADC 精度固定情况下,干扰信号对SINR 影响较大,考虑将用户间信号干扰差值作为有效信道的干扰抑制指标。差值越大,AP 抑制干扰能力越强。为便于分析,将差值转换成比值来评估信道状态环境,其占比形式为:

将γ、B按上述指标转换成一个新矩阵P,第k个用户按照上述指标的排序结果为:

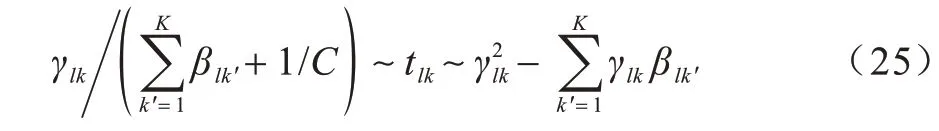
式(24)的排序方式不仅能比较不同AP 服务下用户的SINR 性能,而且体现有效信道对干扰信道的抑制效果,则排序相对合理。
3.3 ADC 精度与AP 组合筛选
按照改进方式排序后,利用所得索引对第k个用户与所有AP 间的实际信道及估计信道的方差系数进行排列,分别为同时,其他用户对第k个用户的干扰信道参数按索引同步排列,则可得其中k'≠k。
基于排序索引选择AP 组合对第k个用户联合服务,则前l个AP 服务第k个用户的SINR 为:

比较排序后多个AP 服务的频谱效率差值来确定服务第k个用户的AP 集。首先确定阈值δ,并比较前l个与前(l-1)个AP服务第k个用户所达频谱效率的差值,大于阈值继续进行筛选,直到遍历完所有AP;若小于阈值则停止筛选,并确定前(l-1)个AP为服务第k个用户的AP 组合。不同的用户对应不同的筛选结果,设用户筛选后所得AP 索引矩阵为。
用户通过利用基于信号干扰差值的AP 选择算法遍历所有AP 进而确定自己的AP 组合后,此时第k个用户的SINR 为:
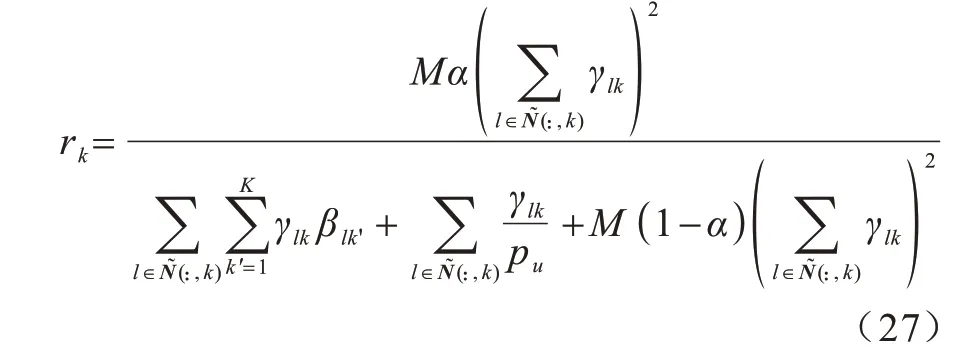
由于回程功耗部分的流量控制的总功耗与选择的AP 组合有关,此时的总功耗为:

因此,通过式(27)、式(28)可得到经过AP 选择后的频谱效率Rk及总的能量效率η。
基于ADC 精度和AP 选择的能效均衡方法的求解过程如算法1 所示。
算法1基于ADC 精度和AP 选择的能效均衡方法的求解算法

在能效均衡方法中,首先基于信号干扰差值对AP进行排序,然后通过比较AP 联合服务的频谱效率变化差值,确定所选AP组合,其复杂度为O(K(L+(L-1))),最后为实现能效质量均衡,在此基础上增添ADC 精度的选择。由于搜索ADC 量化位数的区间为1~10,且为整数,其搜索长度为N=10,所提方法整体的复杂度为O(KN(L+(L-1)))。另外,其他AP 选择一般基于大尺度衰落系数等指标对AP 进行排序,并比较排序后该指标累加和与所定阈值的大小,从而确定所选AP,其复杂度为O(K(L+L))。因此,在去蜂窝大规模MIMO系统中,所提能效优化方法、AP 选择和其他AP 选择的复杂度比较结果为O(KN(2L-1)) >O(K(2L-1)) ≈O(2KL)。由此可以看出,本文的能效均衡优化方法仅为与AP 数L相关的一次函数,故其算法复杂度与对比算法差距较小。
3.4 最大化最小频谱效率的功率控制
在平均功率传输下,通过上述能效均衡方法获取最优ADC 量化及用户对应的AP 组合后,对区域用户的传输功率进行重新分配,以保证系统一致良好的通信服务质量。此时,第k个用户的SINR 表示为:
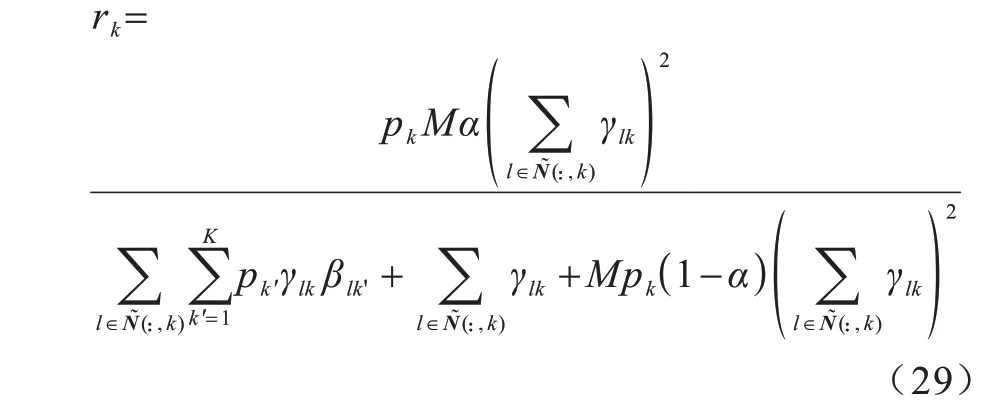
在上行传输系统中,最大化最小用户频谱效率的功率优化问题表示为:
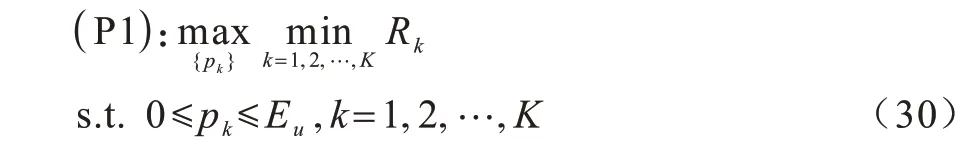
此时,上述优化问题是非凸的,为解决这个问题,通过引入中间变量t及利用一阶泰勒展开的连续近似技术将优化目标变换为非凸问题,即首先将用户的SINR 函数转换为凸函数的形式,其中u>0,v>0,则满足以下条件:

对第k个用户,uk为式(29)分子部分的倒数,而vk则为该公式的分母部分,且第k个用户的SINR 即rk有如下不等式:

其中:uk0和vk0的初始值分别为平均传输功率的对应值。优化问题可转换为:
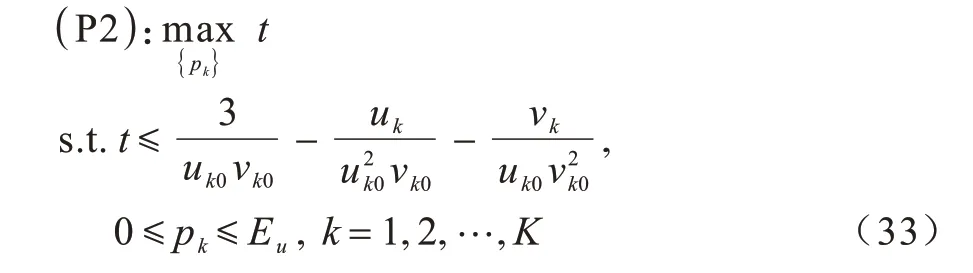
通过上述的近似分解[25],优化问题可转换为求解一系列的凸优化问题。此时,可通过CVX 凸优化工具包进行最优解查找,则最大化最小用户频谱效率的功率优化算法的求解过程如算法2 所示。
算法2最大化最小频谱效率的功率控制方法的求解算法

4 仿真结果与分析
为验证本文所提的基于ADC 精度及AP 选择的能效均衡方法的有效性,本节分析了不同系统参数下多种AP 连接方式对频谱效率及能量效率的影响。仿真中设定信息传输的范围是面积为S(A)=1 km2的正方形区域。在该区域中,用户服从密度λU=10 的泊松分布,所有AP 随机分布,AP 总数L=100,且每个AP 配置的天线数M=3。其中发射导频与数据的平均传输功率均为0.1 W,相干间隔长度τc=200,导频长度τp=40。大尺度衰落系数建模为βlk=-34.53-38 lgvlk+Flk[26],其中,Flk和vlk分别为相关阴影衰落系数和不同环绕情况下的最小值的距离。实验结果均为1 000 次AP 与用户随机分布求取平均值所得。系统的相关仿真参数如表2 所示。
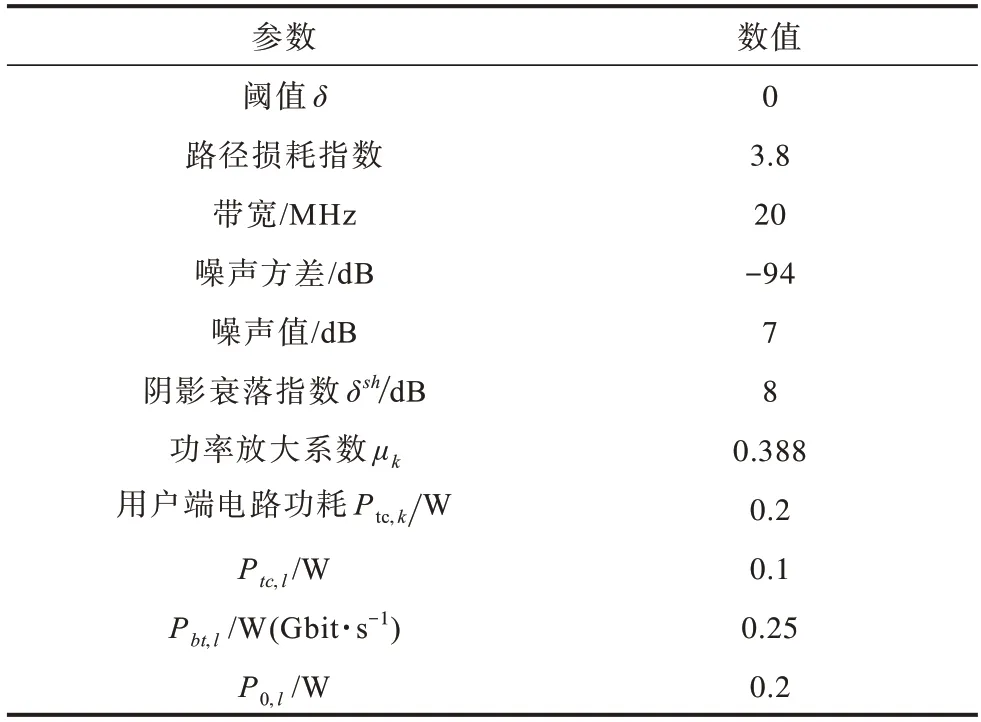
表2 仿真参数Table 2 Simulation parameter
图1 所示为讨论小区内用户分布密度分别为λU=10 和λU=20 时,配置高精度ADC 的AP 数目对总的频谱效率的影响。

图1 接入点数与总的频谱效率的关系Fig.1 Relationship between the number of access points and the total spectral efficiency
从图1 可以看出,在相同用户分布下,通过各种AP 传输方式,总的频率都随着AP 数的增加而逐渐增大,并趋于稳定。因为同AP 服务下的用户间干扰会使增多AP 对总的频谱效率的提升效果趋于饱和,因此有必要合理选择AP 数目。同时,在λU=10 和λU=20 情况下将几种AP 选择算法与全AP 传输进行比较,可以看出AP 选择算法在λU=20 时对性能提升效果更为显著。这是由于用户密集区域,用户间干扰影响较大,更需要为用户进行AP 选择。另外,随着AP 数目的增多,相比于其他AP 选择,所提出的AP 选择算法对系统总的频谱效率一直有更平稳的提升。
图2 所示为当导频长度τp=50 且AP 总数分别为100 和500 时,通过不同AP 选择用户平均频谱效率与ADC 量化位数的关系。
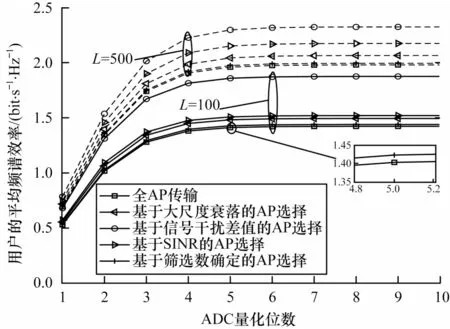
图2 ADC 量化位数与用户平均频谱效率的关系Fig.2 Relationship between ADC quantization bits and average frequency efficiency of users
从图2 可以看出,在本文仿真环境中,当ADC 量化位数从1 逐渐增大时,用户平均频谱效率逐渐增大并在量化位数为4 左右时趋于平稳,此时即使提升ADC 精度,对频谱效率的提高影响也不大。另外,在AP 总数不变的情况下,与全AP 传输相比,利用AP 选择算法时的用户平均频谱效率性能更好,因为AP 选择能通过筛选AP 组合有效减轻用户间干扰。通过与基于大尺度衰落系数、SINR 和筛选数确定的AP 选择算法进行比较,由于考虑了用户间干扰对频谱效率的影响,可以看出本文提出的AP 选择在不同用户分布密度下都可以得到更优的平均频谱效率,并基于筛选数确定AP 选择。另外,AP 的增多也会带来部署及能耗问题,同时在L=500 时进行全传输的频谱效率性能相较于L=100 时提升幅度并不显著。这是因为在区域中增加AP,同AP 下的用户间干扰会相应增大,增加AP 对系统的性能提升效果并不理想。
在射频链路配置量化位数为4 的ADC 和用户传输功率满足功率缩放条件下,用户分布密度分别为λU=10 及λU=20 时AP 天线数与总的频谱效率的关系曲线如图3 所示。其中总的传输功率Eu=20 dB且满足条件pu=Eu/(M×L)。从图3 可以看出,在相同用户分布下,用户平均频谱效率随着天线数增加而逐渐提升并趋于平缓。AP 天线数增加,总的频谱效率性能会因天线带来的分集增益而增强;在功率缩放条件下,AP 天线数的增加也使得用户平均传输功率减小,对频谱效率提升效果趋于饱和。另外,用户分布密度λU=20 比λU=10 时的平均频谱效率性能要差,这是因为用户越密集,用户间干扰越强,此时所有AP 选择算法对性能提升效果都更显著。在λU一定时,相比于其他算法,基于信号干扰差值的AP选择对频谱效率的提升效果更好。

图3 接入点天线数与用户平均频谱效率的关系Fig.3 Relationship between the number of antennas of access points and the average spectral efficiency of users
图4 所示为用户数期望=10 且小区面积分别为S(A)=1 km2和S(A)=4 km2时,AP 数对总的能量效率的影响。
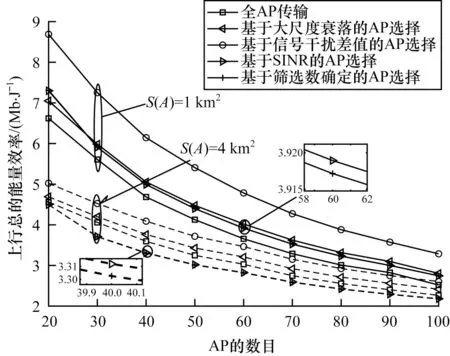
图4 接入点数与能量效率的关系Fig.4 Relationship between the number of access points and energy efficiency
从图4 可以看出,AP 数目越多,能量效率越小。这是由于AP 数目越多,用户间干扰也尤为显著,全AP 传输中无效AP 也越多,其不必要的功耗也会增多。图中显示随着区域面积越大,总的能量效率越小,且在相同AP 数目下,造成的平均路径损耗也会更大,信号衰落也更严重,因此达到一定频谱效率需要消耗更多功耗。同时,在S(A)=1 km2的区域内,所有AP 选择算法都对总的能量效率有较大提升,且在密集区域,通过AP 选择算法对性能提升效果更为明显。在S(A)=4 km2时,基于筛选数确定和基于SINR 的AP 选择并不比全AP 传输下的能量效率性能要好,选择的无效AP 组合更多,即该算法并不适用于用户密集的信息传输区域。相比其他AP 选择算法,在AP 总数一定时,所提基于信号干扰差值的AP 选择算法的能量效率提升效果更好。因为该算法针对性地考虑了用户间干扰的抑制能力,选择的AP 组合更为有效。
图5 所示为用户分布强度λU=10 时,不同ADC精度下系统总能量效率和总频谱效率之间的权衡。
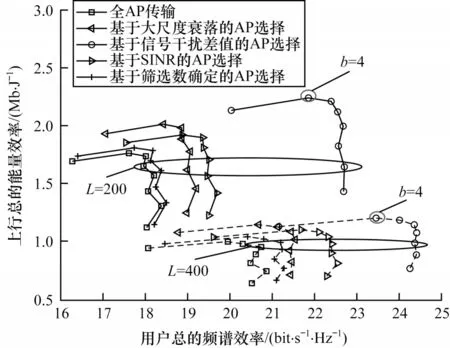
图5 不同ADC 量化下能量效率与总频谱效率的关系Fig.5 Relationship between energy efficiency and total spectral efficiency under different ADC quantization
从图5 可以看出,系统AP 部署的增多虽然能带来更好的频谱效率性能,但是能量效率也大幅降低。这是因为AP 部署越多,其带来的干扰信号也随之增多,即无效AP 占比更多,消耗的功率增多,使得系统能效降低,因此有必要合理部署AP 数目及进行AP 选择。另外,相比于其他AP 选择模式,基于信号干扰差值的AP 选择算法对用户平均频谱效率及能量效率都有更好的提升。对于较低精度的ADC,量化位数越大,能效及频谱效率都有较大提升,但在较高精度时能效开始逐渐降低。因此,在图中拐点处即最优量化位数为4 时可实现本文仿真环境下的能效均衡。
在本文仿真环境中配置最优量化的ADC 时,分别利用不同AP 选择策略及联合最大最小功率控制下用户频谱效率的累积分布函数曲线如图6 所示。仿真结果显示,相比其他AP 连接模式,基于信号干扰差值的AP 选择能针对每个用户实现频谱效率的提升,且在通过该选择策略获取较优AP 组合基础上,利用最大最小用户频谱效率的功率控制,可提升服务质量较差的用户通信性能,减小不同用户间的频谱效率差距,在系统区域内实现用户服务质量一致的优化目标。因此,可验证通过本文所提的能效均衡优化方法获取最优量化位数及AP 组合后,利用最大最小频谱效率的功率控制算法可实现系统区域一致良好的服务质量。
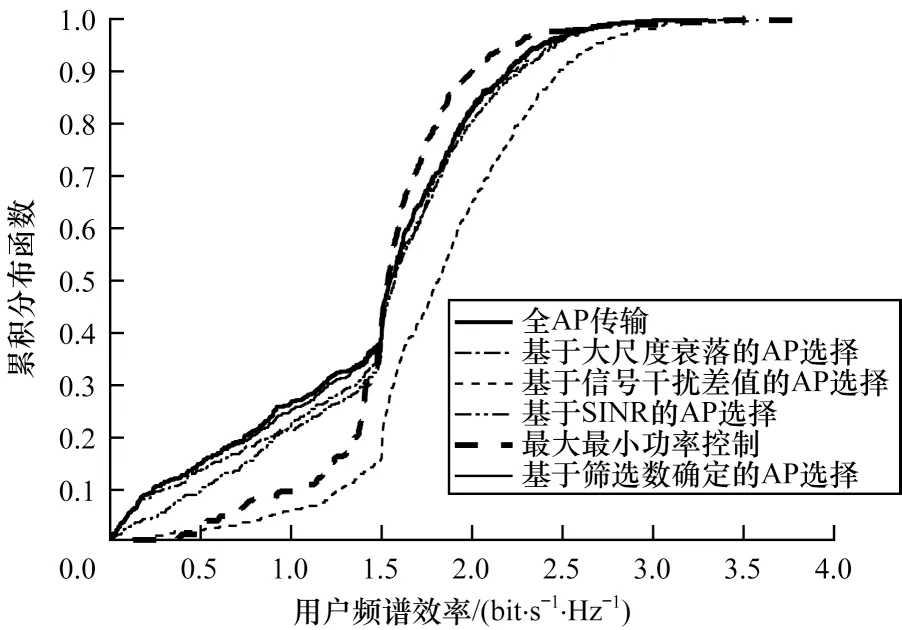
图6 每个用户频谱效率的累积分布函数Fig.6 Cumulative distribution function of spectral efficiency per user
5 结束语
本文针对去蜂窝大规模MIMO 系统的能效质量失衡问题,提出一种ADC 精度和AP 选择的能效均衡方法。该方法将信号干扰差值作为衡量信道干扰抑制能力的指标,对AP 进行降序排列,并根据比较排序后AP 联合服务的频谱效率变化差值筛选AP 组合。通过ADC 精度和AP 选择联合优化,实现频谱效率及系统能效的均衡,确定最优量化位数,最终利用最大最小的功率控制实现系统性能的进一步优化。仿真结果表明,本文方法对频谱效率与能量效率能产生双重提升效果,与基于大尺度衰落、SINR和筛选数等指标的AP 选择相比,在不同的用户分布密度、AP 数或天线数时都能实现更优的系统能效均衡,尤其在用户密集区域,效果更为明显。本文提出的能效均衡方法适用于导频资源充足的情况,考虑高热点时导频污染问题对该方法的影响将是下一步的研究重点。

