基于TLBGA-GRU 神经网络的短期负荷预测

吴铁洲，邹 智，姜 奔，张晓星

（1.湖北工业大学电气与电子工程学院，武汉 430063；2.湖北工业大学太阳能高效利用及储能运行控制湖北省重点实验室，武汉 430063）

0 概述

在当前新能源渗透率越来越高的新型电力系统中，负荷预测是确保其平稳高效运行的重要保证［1］。负荷预测方法按照预测的时间范围来划分［2］，长期与中期预测通常是从几个月到几年，短期预测的预测范围则是从几小时到几周［3］。HERNANDEZ 等［4］在对实际案例进行研究后发现，对于电网来讲，短期负荷预测具有独特的使用价值。短期负荷预测结果经常被用来协助制定一周内电力系统的机组启停、机组最优组合、经济调度、最优潮流及影响电力市场交易等。预测精度越高，越有利于提高发电设备的利用率、经济调度的有效性和日常多个时间范围内电力运行的可服务性［5］。

HOSSEN 等［6］将深度神经网络（Deep Neural Network，DNN）应用到短期负荷预测中，相较于浅层人工神经网络，DNN 虽在预测精度上有所提升，但仍需人工提取时序特征。长短期记忆（Long Short-Term Memory，LSTM）网络是一种专门处理时间序列数据的循环神经网络（Recurrent Neural Network，RNN），它解决了RNN 的梯度消失和爆炸以及长期记忆不足的问题［7］。而门控循环单元（GRU）是在LSTM 的基础上进行改进优化的神经网络［8］。与LSTM 相比，GRU 在具有同等准确率的情况下，拥有更低的复杂度及更快的收敛速度来捕获不同时间步长的长短期依赖性关系［9］。

此外，在深度学习领域中，不同类型神经网络的准确性和收敛性很大程度上依赖于超参数（如隐藏层的数量和每层神经元的个数）［10］。而超参数的设置在先前都是手工调试的，需不断进行调整试错，在调整试错过程中比较依赖其调参的先验知识，容易陷入局部最优解，很难获得合适的超参数。文献［11］分析认为，目前主要有3 种方法寻找最佳超参数。网格搜索（Grid Search，GS）通过引入最小代价函数或最高适应度函数的组合获得超参数的最佳集合［12］。然而，GS 在运行时需要运用大量的算力才能获得最佳的网络架构。而随后提出的随机搜索（Random Search，RS）方法虽然可以避免运算量大的缺点，但其无法保证得到全局最优超参数［13］。另外，RS 在超参数域中进行的是盲目搜索，但这种方式效率较低，难以求解复杂问题。为了解决该问题，研究人员提出采用遗传算法等元启发式算法搜索超参数。因为GA 在运行过程中，首先保存了每个步骤中具有最佳结果的超参数组合，然后通过上一步的超参数来生成下一步中的新超参数集。可以看出，其搜索过程不是盲目的，找到最优结果的可能性比RS更高。文献［14］对GS、RS 和GA 的精度和计算时间进行了比较研究，在CIFAR-10 分类数据集上的结果显示，GA 算法明显优于提到的其他算法。

GA 算法在运行早期容易产生超级个体，出现早熟收敛现象，从而导致算法过早地收敛于局部最优，而非全局最优［15］。在过去的几年中，研究人员一直致力于改进GA 算法的性能，以提高该算法在处理不同优化问题时的有效性。研究人员已经证明了GA算法的效率直接取决于算子和策略参数的选择［16］。关于变异算子，大多数研究都试图确定最佳的变异种类或变异率。然而，更常见方法是动态调整变异，而不是固定变异率统一应用于整个种群［17］。BEHROOZI 等［18］提出一种基于教与学优化（Teaching Learning Based Optimization，TLBO）的新型变异算子，在解决早熟收敛问题的同时，还提高了GA 算法的性能。该方法采用一种高智能的变异算子，选定的基因将智能地突变，以使染色体接近更好的解决方案，而不是随机变异。因此，为解决GA 算法的早熟收敛问题，可以从变异算子入手，通过改变变异为种群补充新的个体，增加种群的多样性，使算法跳出局部最优。

本文提出一种基于TLBGA-GRU 神经网络的短期负荷预测方法。采用灰色关联分析法对原始数据进行分析，剔除冗余特征，将剩余的主要特征保留并输入到GRU 神经网络中。随后通过TLBGA 算法对GRU 神经网络进行超参数调优，在得到预测精度更高、性能更好的模型后，再将筛选的数据输入到该模型，从而输出负荷预测的结果。

1 TLBGA-GRU 神经网络模型

1.1 GRU 循环神经网络模型

经研究发现，由于RNN 网络中存在循环单元结构，允许输入特征持续存在，这也就使得RNN 具有一定短期记忆能力，因此RNN 网络在处理时间序列数据方面具有一定的优势。然而，RNN 还是存在阶梯消失问题，因此随着时间间隔的增加，RNN 会逐渐失去学习旧信息的能力。

LSTM 是一种特殊的循环神经网络，其很好地解决了RNN 中梯度消失的问题。但是，在后续的研究中发现，LSTM 由于其内部参数与数据较多，比较复杂，会降低其训练效果［19］。为了更好地解决这个问题，研究人员提出了GRU 神经网络，其内部采用门控循环神经网络结构，相比于LSTM，训练参数较少，收敛速度更快［20］。图1 所示为GRU 神经元内部结构，计算公式如式（1）所示。

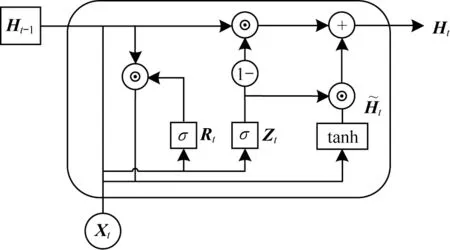
图1 GRU 神经元内部结构Fig.1 Internal structure of GRU neuron

在图1 与式（1）中：Rt表示重置门；Zt则表示更新门；Xt与Qt分别表示t时刻的输入与输出向量；Ht和表 示t时刻的隐藏状态与候选隐藏状态［21］；Wxz、Wxr、Whr、Whz、Wxh、Whh、Whq是权重参数；br、bz、bh、bq是偏差参数；⊙表示矩阵的数乘；1-表示该链路向前传播的数据为1-Zt；σ表示的sigmoid 函数可以将元素的值映射到［0，1］范围内，因此重置门Rt和更新门Zt中每个元素的值域都是［0，1］［22］。

1.2 基于TLBGA 算法的GRU 优化实现

1.2.1 TLBGA 算法

自动寻找最优超参数的方法较多，如粒子群优化算法、蚁群算法、模拟退火算法以及遗传算法。与遗传算法相比，其他算法受初始值的影响较大，只能找到问题的局部最优解。遗传算法是一种基于遗传和变异的模拟生物进化机制的自适应优化算法，可以有效搜索多参数组合问题的目标函数值（充分接近最优值）［23］。与传统算法相比，遗传算法的优势在于可以使用概率、启发式规则进行最大搜索，从而比较适合大规模问题以及多维多模态问题的求解［24］。

原始的GA 算法存在早熟收敛问题，很容易由于种群缺少多样性个体而陷入局部最优。为解决上述问题，本文在算法中加入一种基于TLBO 方法的新型变异算子，在解决早熟收敛问题的同时，还可以提高解的质量以及算法的收敛速度。这种算子可以让选定的基因智能突变，以使染色体接近更好的解决方案，而不是随机改变。因此，在每一代遗传算法中，如果将基于适应度的最佳解决方案视为教师，则其他染色体的选定基因会因教师的相同基因而发生突变。基于TLBO 的智能变异算子运算公式如式（2）所示：

其中：Tf为教学因子，它是操作员调整以设置收敛速度的设定系数，此参数的值在0～1 之间随机选择；DGk，j表示第k个学习者的基因j的平均值与教师当中相同基因j的值之间的差值；表示第k个学习者的基因j的更新值。

TLBO的效果基于教师影响学生知识的教学过程。学生和教师是班级的两个主要因素，该算法解释了通过教师（称为教师阶段）和跟随学生之间的讨论（称学生阶段）进行学习的两种模式。该算法的总体由班级的一组学生（即学习者）组成。为学习者提供的不同主题与优化问题的不同设计变量类似。班上最好的学生在每次迭代中成为老师，其他学生通过最好的学生的影响提高他们的体能。图2 所示为基于教与学的变异（Teaching Learning Based Mutation，TLBM）算子的运行流程。图3 所示为TLBGA 算法的运行流程。

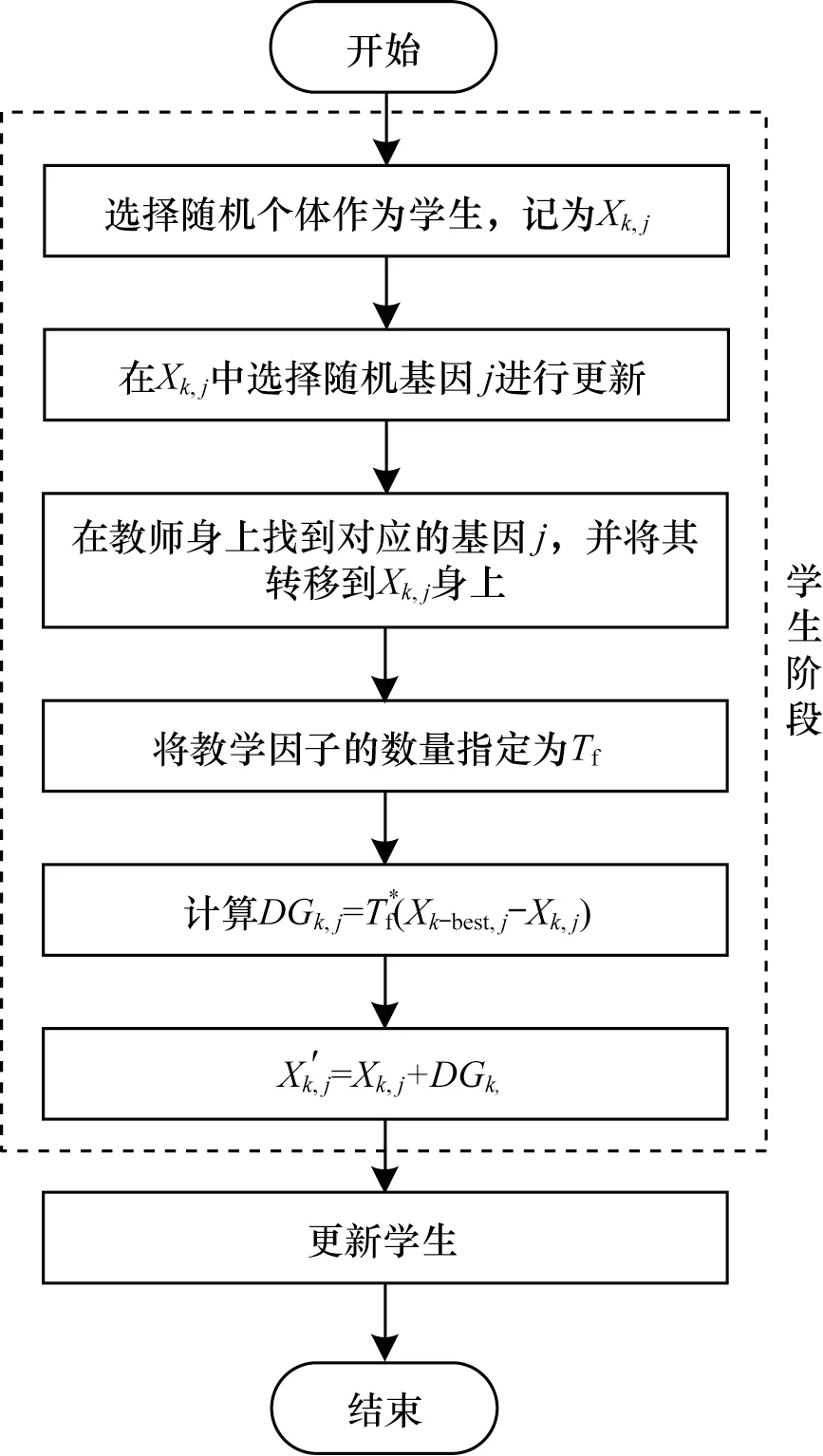
图2 TLBM 算子运行流程Fig.2 Procedure of running of TLBM operator

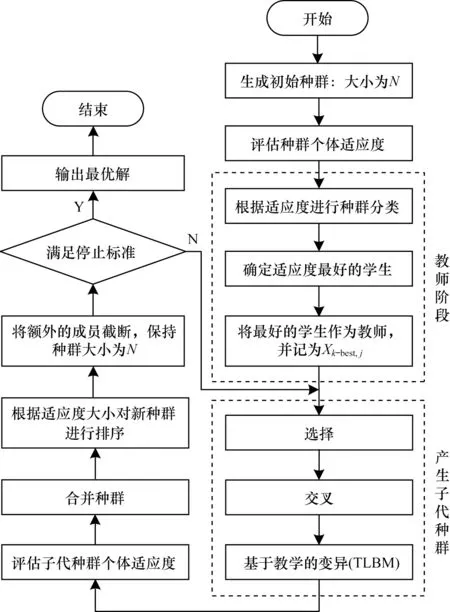
图3 TLBGA 算法运行流程Fig.3 Procedure of running of TLBGA algorithm

算法具体步骤如下：

1）将需要寻优的超参数输入GA，生成初始种群，并评估适应度；对适应度进行排序，选取适应度最高的个体作为教师。

2）进行选择、交叉以及基于教学的变异，在TLBM 中，通过教师引导学生以及学生与学生直接讨论，两种方式引导突变。

3）评估子代种群个体适应度，并进行排序，选取排序后的前N个个体组成新种群，剩余个体舍弃。

4）判断是否满足收敛标准，若不满足，则返回第2 步；若满足，则到第5 步。

5）输出最优解，得到最优超参数，结束。

为验证TLBO 智能变异算子的有效性，本文将该算子与其他变异算子进行了比较，如经典变异遗传算法（Classic Mutation Genetic Algorithm，CMGA）、交换变异遗传算法（Swap Mutation Genetic Algorithm，SMGA）、转位变异遗传算法（Inversion Mutation Genetic Algorithm，IMGA）和爬行变异遗传算法（Scramble Mutation Genetic Algorithm，ScMGA）。

如表1 所示，经过150 次迭代，SMGA、IMGA 和ScMGA 3 种算法得到的结果几乎是相似的，而TLBGA 分别为2～5 个自变量的Sphere 函数找到了10-104、10-75、10-53和10-44大小的结果。因 此，可以很明显地看出TLBGA 算法在寻优后得到的解比其他算法具有更高的质量。

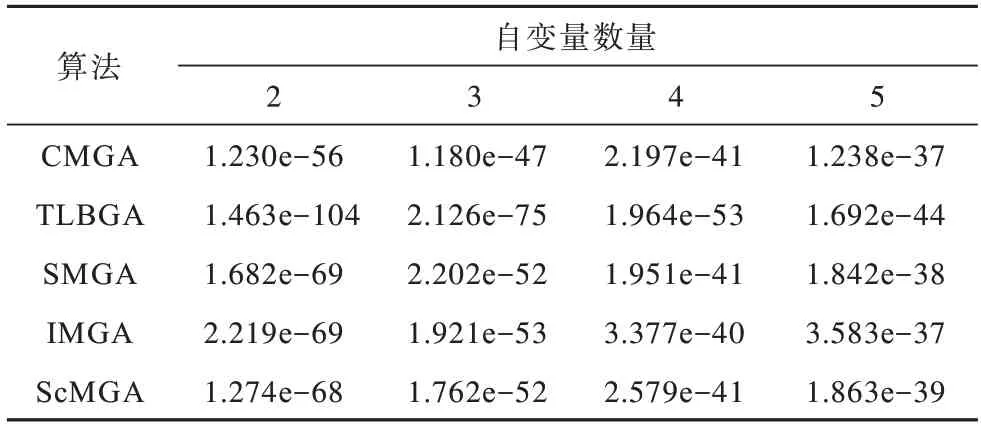
表1 Sphere 函数150 次迭代的最佳结果Table 1 Optimal results of 150 iterations of Sphere function

1.2.2 超参数寻优

在机器学习中，超参数寻优的本质其实就是对损失函数进行最优化的过程，用算法去寻找损失曲面的全局最优解，从而避免陷入手工寻优中由于先验知识导致的局部最优解［25］。

将Sphere 函数图假定为损失曲面图，如图4 所示，损失曲面中不同的路径代表着一组组不同的超参数组合，比如当选择不同的激活函数时，其模型每一层的输出也会不同，从而导致寻优路径产生根本差异，尤其是在高维空间下。

图4 损失曲面示意图Fig.4 Schematic diagram of loss surface

本文用DNN 神经网络举例，其输出计算如式（3）所示：

其中：X是包含训练点位置的向量；Z1是第1 层的输出；σj、ωj和bj分别是与第j层相关联的激活函数、权重和偏置向量；U是输出向量；下标M表示第M层，即输出层。含有两个隐藏层的DNN 模型结构如图5 所示。

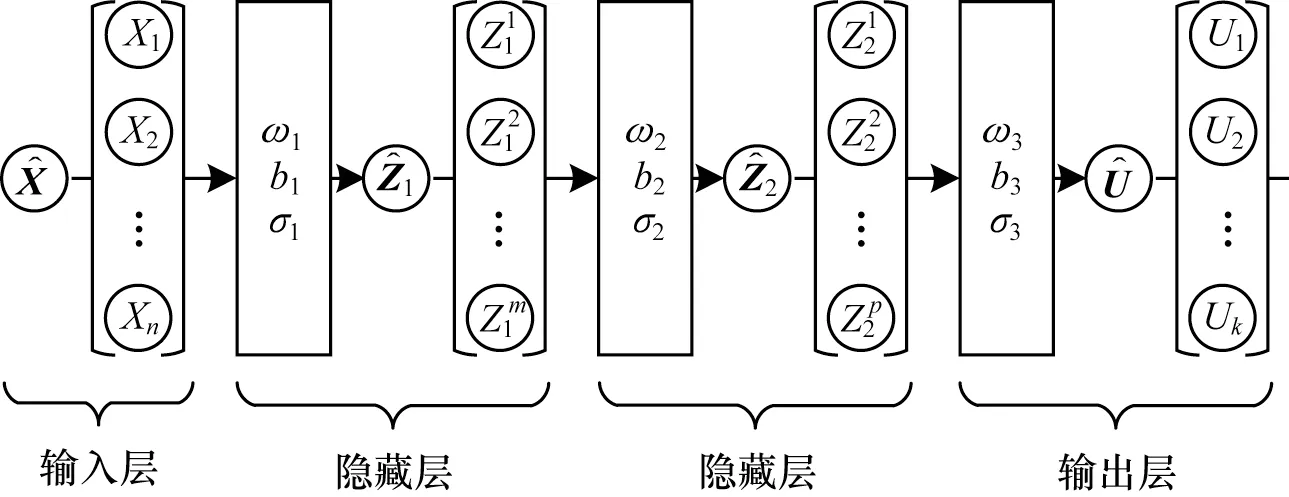
图5 DNN 神经网络结构Fig.5 Structure of DNN neural network

如果没有激活函数，该模型就只是线性回归模型，无法分析复杂的输入数据。激活函数是一个线性或非线性函数，用作相邻层之间的数学门，以便每层的输出通过激活函数到达下一层。因此，超参数在很大程度上影响模型的收敛速度和精度。

1.2.3 基于TLBGA 优化超参数

使用TLBGA 算法在连续优化中寻找超参数时，必须考虑两个先决条件：1）确定染色体；2）用于评估生成的解决方案的适应度函数［26］。在这种情况下，使用二进制数组对基因片段进行编码。图6 所示为基因片段图解。

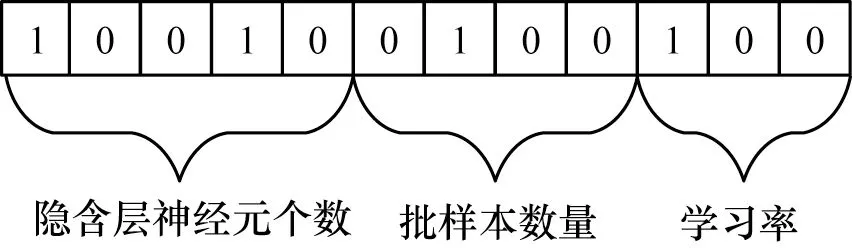
图6 基因片段图解Fig.6 Gene fragment diagram

第1位到第5位表示隐藏层中神经元个数，第6位到第9 位表示批样本数量，剩下的位用来表示学习率。将交叉熵的倒数作为适应度函数，以实现目标最大化，如式（4）、式（5）所示：

其中：为实际的概率分布值；gi为预测概率分布值。

针对本文中的GRU 神经网络模型，选择了对模型性能影响较大的3 种超参数进行寻优，分别是隐藏层神经元个数、批样本数量以及学习率。如其中的批样本大小，当它过小时，代表输入网络的数据样本数过小，从而不具代表性，导致网络难以收敛；当它过大时，又会使梯度方向过于明确，容易陷入局部最优解，降低精度。表2 所示为本文GRU 网络超参数的选择范围。

表2 GRU 网络超参数选择范围Table 2 GRU network hyperparameter selection range

1.3 TLBGA-GRU 模型预测步骤

本文采用TLBGA 算法对GRU 神经网络进行优化，将GRU 神经网络的隐含层神经元个数、批样本数量及学习率看作待优化值，以输出误差作为目标函数，利用迭代取得最优解。具体步骤如下：

1）特征工程阶段。对历史数据进行预处理，选取输入特征，利用灰度关联法对原始数据进行关联度分析，剔除冗余特征，保留关联度高于均值的特征并组成新的特征集。

2）问题与超参数确认阶段。将需要寻优的部分输入TLBGA 算法。首先对隐含层神经元个数、批样本数量及学习率进行编码，再利用TLBGA 算法对其进行迭代寻优，若满足停止条件，就将其输回GRU 模型中，进行超参数更新。

3）预测阶段。将数据分为训练集与测试集，利用训练集对TLBGA-GRU 模型进行训练，优化并更新网络模型参数，使其在对测试集进行预测时拥有更好的效果，最后将筛选后的输入数据输入到训练好的模型中进行预测，从而得到预测结果。

4）评价阶段。通过RMSE、MAPE 和R23 种指标来判断预测结果精度的高低，再经过对比研究得到模型的优劣。

2 负荷预测特征与模型评价指标

2.1 特征关联度分析

电力负荷预测中的影响因素较多，例如天气类型、风力、节假日以及温度等。由于影响因素中存在许多相似或冗余的部分，这些多余的部分浪费大量算力，会使模型的预测精度下降。为了解决这一问题，本文采用灰色关联度分析法对原始因素进行关联度分析，得到各因素之间关联度的大小后再进行筛选。计算公式如式（6）、式（7）所示：

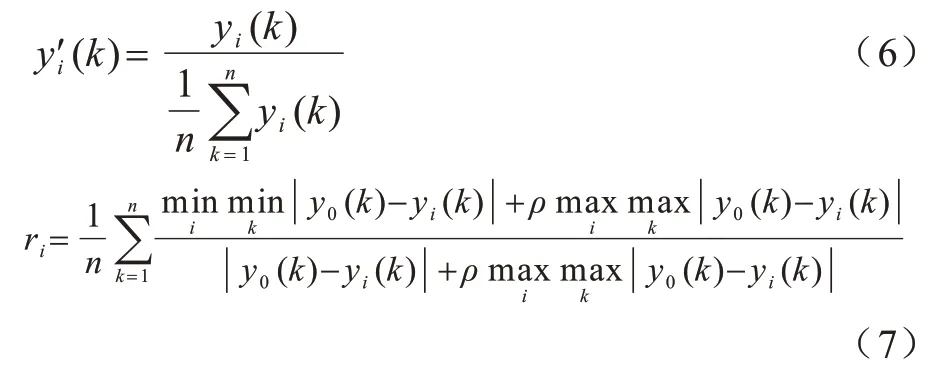
其中：y0表示历史负荷序列；yi表示第i类其他特征序列：表示均值化后的第i其他特征序列；ri表示第i类其他特征与历史负荷的关联度，i∈［1，m］，k∈［1，n］；m为其他特征个数；n为各特征序列的维度；ρ为分辨系数，通常取0.5。

2.2 模型精度评价指标

为了精确地研究TLBGA-GRU 模型的优势，采用平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）、均方根 误差（Rooted Mean Squared Error，RMSE）和决定系数（R2）作为评价标准，表达式分别如式（8）、式（9）、式（10）所示：

其中：n表示预测样本采样点总个数；yi为第i个采样点的实际负荷值；为第i个采样点的预测负荷值。MAPE 与RMSE 的取值范围在［0，+∞）之间，当预测负荷值趋近于实际负荷值时，MAPE 与RMSE 也越趋近于0。因此，当所得预测结果的MAPE 及RMSE越小时，则说明文中模型的预测效果越好。另外，R2越接近1，表示模型的拟合度越好。

2.3 TLBGA-GRU 模型的训练

在模型的训练过程中，本文将TLBGA 算法的训练种群大小T设为20，迭代次数为100，Ps为0.1，Pc为0.3，Pm为15，选用交叉熵的倒数作为适应度函数，GRU 网络的层数d设为3，将Droput 设为0.4 可防止网络过拟合。

3 负荷预测实验与分析

3.1 数据预处理

利用式（4）对所有原始数据进行均值化处理，然后再用式（5）计算历史其他特征因素与最大负荷数据的关联度。表3 所示为计算的关联度结果。

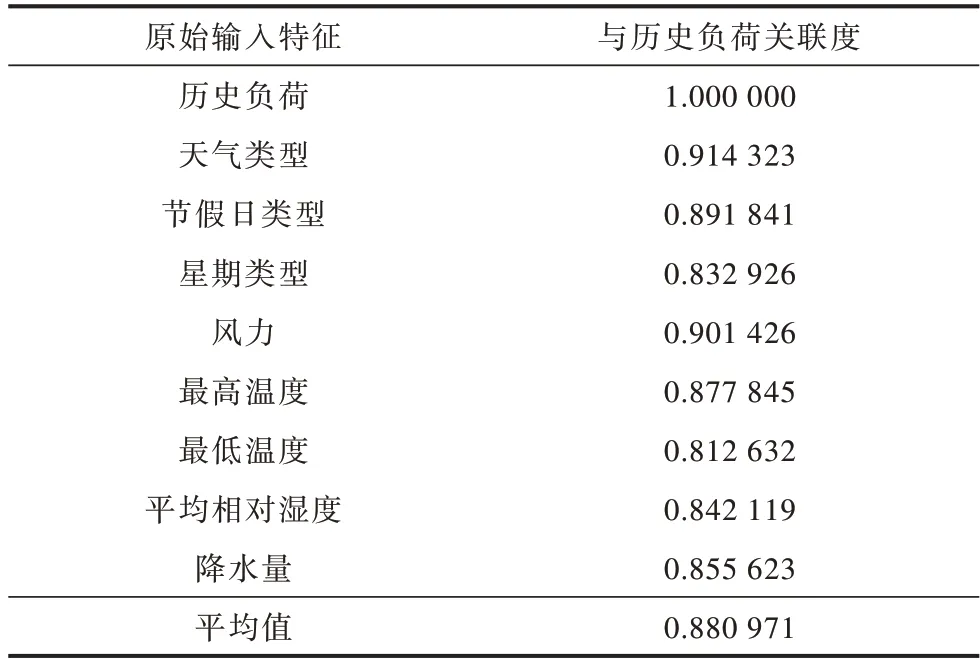
表3 输入特征关联度分析Table 3 Correlation degree analysis of input features

由表3 可知：关联度平均值为0.880 971，本文选取关联度高于平均值的特征组成新的特征集，具体分别为天气类型、节假日类型、风力。最后，将新的特征矩阵输入到神经网络模型中进行预测，从而得到更精确的预测结果。

直接将筛选过后的历史负荷数据、天气类型、节假日类型及风力等特征同时作为GRU 神经网络的输入，会导致输入数据的量纲无法统一，不利于模型参数的优化。为了解决此类问题，可以通过离差标准化将原始数据转化为落在［0，1］之间的数据，将数据量纲归一化，以便实现损失函数较快收敛，其表达式如式（11）所示：

其中：X为归一化后得到的输入数据；x为原始输入数据。

3.2 欧洲某地区电力负荷数据集预测结果分析

为验证所提负荷预测模型的精确性，本文采用欧洲某地区2017年7月6日—2018年7月6日共365日的电力负荷数据，每小时采样一次，其中每天共有24条数据，总共8 760条数据。本文将此负荷数据划分为两个数据集，训练集为前358天，测试集为最后7天，对测试集的日负荷进行预测。为了评估所提方法的有效性，本文对模型进行了训练，并与BP、RNN以及GRU等模型进行比较。各模型误差定量评价结果如表4和表5所示。

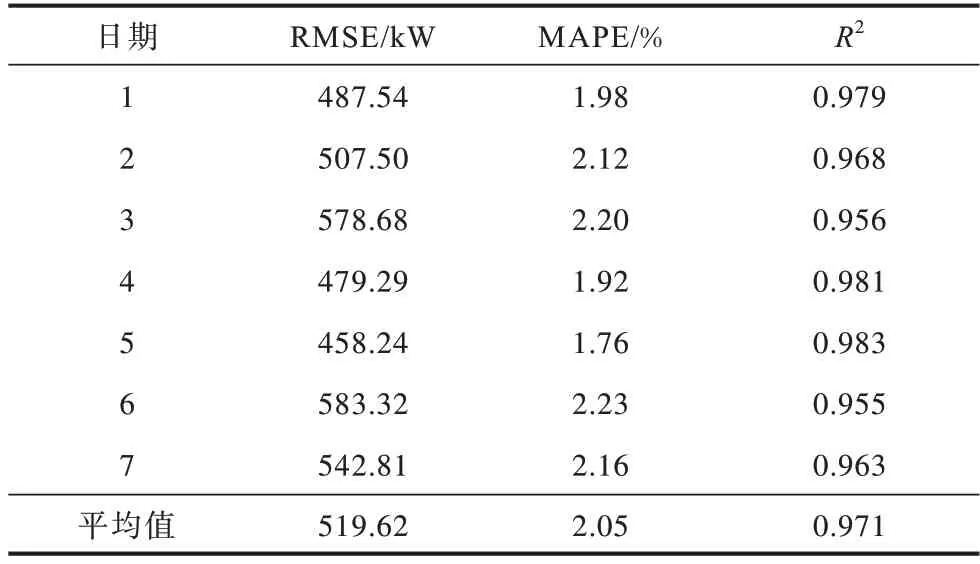
表4 TLBGA-GRU 模型误差定量评价结果Table 4 TLBGA-GRU model error quantitative evaluation results

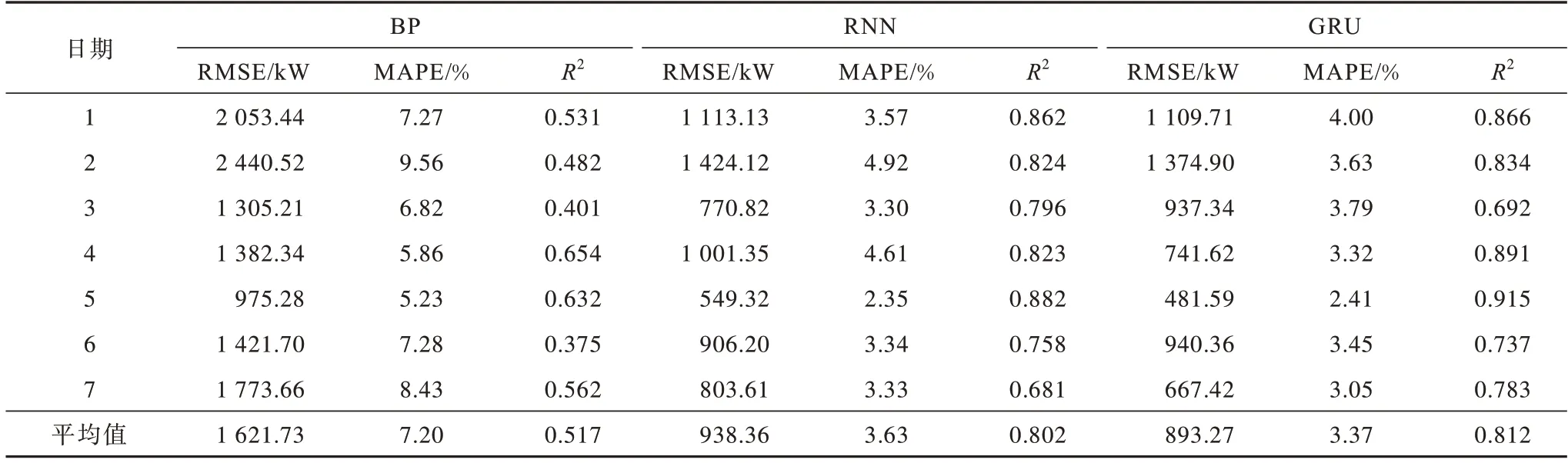
表5 不同模型误差定量评价结果Table 5 Results of quantitative error evaluation of different models

由表4 可知：TLBGA-GRU 的R2平均值为0.971，RMSE 平均值为519.62 kW，MAPE 平均值为2.05%。由表5 可知：对其他模型预测性能的分析表明，GRU 在评分性能指标方面的预测效果最好。GRU 模型的R2平均值为81.2%，高于BP 模型和RNN 模型的平均值。报告的结果包括BP、RNN 和GRU 的均方根误差（RMSE），分别为1 621.73 kW、738.36 kW、893.27 kW。综上所述，相较于其他模型，所提方法在RMSE和MAPE指标上都有明显下降，表明在预测过程中整体预测精度和模型性能都有较大的提升。

图7所示为2018年7月5日15：00—7月6日15：00共24 个小时的各模型短期负荷预测曲线对比。由图7 可以看出：TLBGA-GRU 预测模型预测精度更高，拟合效果也更好。在负荷变化的波谷处，BP、RNN 方法不能准确分析负荷波动规律，会导致精度严重下降，而GRU虽然波动较小，但是整体预测曲线偏右，拟合效果较差。相比之下，本文中TLBGA-GRU 模型能更准确地捕捉负荷波动规律，使预测值更贴近真实值，提高预测精度。

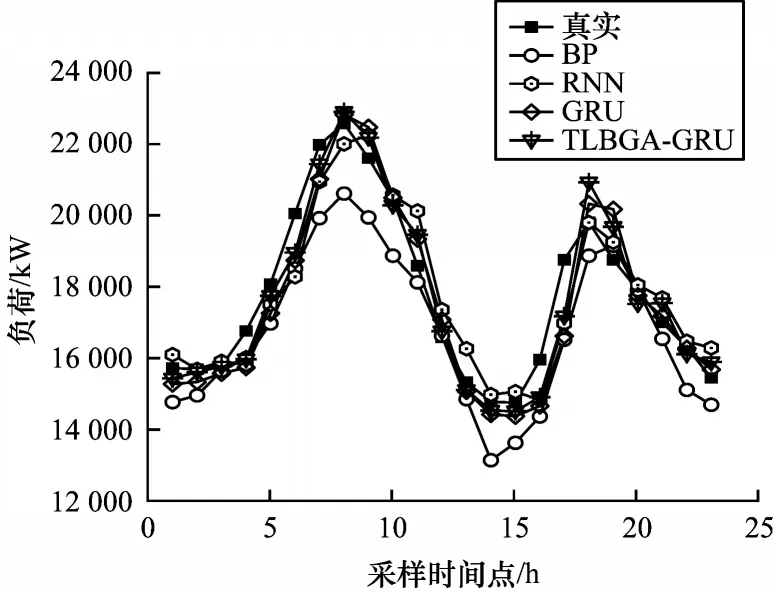
图7 不同模型预测结果对比Fig.7 Comparison of prediction results of different models

3.3 美国PJM电力市场公开负荷数据集预测结果分析

本文选取美国PJM 电力市场提供的某地区的公开数据集进行负荷预测的训练与测试，验证本文所提出模型的有效性。本文数据集包含了该地区2014 年3 月31 日—2014 年4 月30 日接近1 个月的负荷数据，每15 分钟采样一次，其中每天共96 条数据，总共2 880 条数据。本文将前29 天作为测试集，剩下的1 天作为测试集进行负荷预测。

表6 所示为测试集中日负荷不同模型精度对比。由表6 中可知：本文提出TLBGA-GRU 模型的R2的大小与其他模型相比最大，达到97.2%，而TLBGA-GRU 模型的RMSE 与MAPE 相对于其他3 种模型在不同程度上也都有所降低，其中MAPE 分别降低了4.92%、1.27%、0.74%。

表6 不同模型精度对比Table 6 Comparison of accuracy of different models

图8所示为测试集中某天的日负荷预测结果对比。由图8 可知：本文提出的TLBGA-GRU 模型能够比较准确地判断真实负荷的走势，与真实负荷曲线相比有更好的拟合度，因此具有更高的预测精度。

图8 日负荷预测结果对比Fig.8 Comparison of daily load prediction results

4 结束语

本文提出一种基于TLBGA-GRU 模型的短期电力负荷预测方法。通过TLBO 方法解决GA 算法的早熟收敛问题，得到混合后的具有更好寻优能力的TLBGA 算法，并利用其对神经网络中超参数进行寻优，更新优化神经网络模型，克服手动寻优需要借助先验知识的缺陷，从而提高模型的整体预测精度。实验结果表明，该方法与BP 神经网络、RNN 神经网络、GRU 神经网络相比具有更高的精度。由于本文模型在负荷预测中对最终结果产生影响的因素种类较多，因此下一步将对数据的特征工程进行改进，提取输入特征，以提高预测模型的普适性及精度。