依赖动量转移条件下的残留电子屏蔽效应
陈展斌,王 军
(湖南工业大学 理学院,湖南 株洲 412007)
1 研究背景
量子散射/碰撞是探究原子结构和各种物理效应的重要手段之一。在入射电子能量很低的情况下,碰撞电离过程中各种相互作用将发挥重要作用。研究低能区的碰撞不仅有利于人们揭示碰撞过程中的物理效应,而且能更好地检验各种近似模型的有效性[1-9]。
(e,2e)反应是最常见的一种碰撞过程,涉及的碰撞对象可以是原子、大分子和团簇等。通过对碰撞末态产物状态(如散射物质的电荷态、出射电子的能量、角分布和反冲离子)动量的分析,可以揭示物质内部的结构和相互作用。
近年来,伴随多通道动量谱仪的成功应用和全空间反冲动量谱仪分辨能力的提升,一些新的实验现象被陆续发现。He 原子是研究关联动力学理想的靶原子,其(e,2e)反应是研究的热点。理论上,一阶玻恩近似适用于高能(e,2e)反应,但不能正确给出recoil 峰的幅度和谱线轮廓。高阶模型如二阶玻恩近似虽给出了合理的形状和幅度,但其推导过程非常复杂。密耦合方法在计算(e,2e)反应时所得结果与实验测量之间也存在较大差异。其主要原因在于一些特殊条件下,入射电子和出射电子波函数不能正确描述碰撞的实际情况,在距离核较远的区域,慢电子渐进行为被忽视了。H.R.J.Walters 等[1]发现在共面条件下,多种理论方法计算的He 原子(e,2e)反应截面均能与实验测量吻合,但在非共面条件下理论计算的幅度均小于实验结果。他们推断理论和实验测量的差异可能来源于角向分布函数的处理。Zhang Z.等[2]在测量敲出电子能谱时发现所得结果与其它实验测量结果并不一致。在一些特殊条件下,二阶玻恩近似模型仍不能给出合理解释。J.Berakdar等[7]利用扭曲波方法计算了He 原子(e,2e)反应的三重微分截面(TDCS),发现微分截面在很大程度上取决于非零角动量和扭曲电子。Sun S.Y.等[10]采用全非微扰方法计算了He 原子(e,2e)反应的散射截面。结果表明靶离子的极化在He 原子单离化过程中非常重要。考虑极化效应后的结果与实验数据符合程度较高,但单离化与双离化截面的比值还需进一步实验和理论证实。此外,还有一些其它关于理论预言与实验测量不一致的情况[11-12]。
对于He 原子(e,2e)反应,目前还有很多问题没弄清楚。在中低能入射情况下,很多物理效应对截面的影响没有统一定论。B.A.De Harak 等[3]测量了共面条件下入射能为150 eV,敲出电子能量为34.5 eV,敲出电子角θb为75°,90°,-105°时,氦原子(e,2e)反应中TDCS 随θa在-40°~40°的变化情况。这种实验几何安排比较特殊,其角度变化很小但动量转移非常大,称为截面依赖动量转移几何安排。
然而,虽然实验已过多年,但鲜有在该几何条件下的理论报道。特别是,作为一种具有清晰图像的物理效应,残留电子屏蔽效应在该特殊几何安排下的影响还没有被揭示过。这里需要特别注意且容易混淆的是,虽然文字上表述相似,残留电子屏蔽效应和屏蔽效应在物理图像上有着本质区别。残留电子屏蔽效应的物理图像表现在靶态残留电子的存在,对末通道电子所感受到电荷的影响,集中在电子-电子-电子之间“三电子的相互屏蔽作用”。体现在修正模型与DS3C 模型之间的差异。而屏蔽效应是DS3C 和3C 模型之间由于考虑动力学屏蔽而引起的[4],物理图像在于两个出射电子之间屏蔽的影响。集中在“电子-电子-核之间的相互作用”,与靶态残留的第三方电子无关。
本研究利用DS3C 模型[4]系统研究了这种特殊几何安排下He 原子(e,2e)反应截面。并将几种重要的残留电子屏蔽理论引入其中。计算了不同散射能量、不同入射能量、不同散射角度情况下的TDCS,通过与实验测量进行对比,揭示了靶原子结构特征和碰撞过程之间的关系。探索了不同理论模型下残留电子屏蔽效应对截面的影响。
2 理论方法
TDCS 给出了碰撞过程较为完整的动力学描述。通常用公式(1)描述(e,2e)反应过程[4-5]:
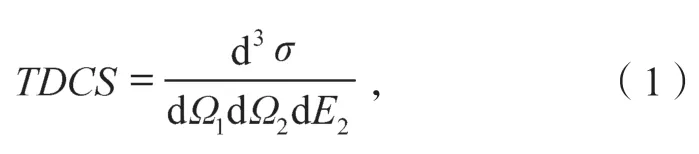
其物理意义为(e,2e)反应后两自由电子在立体角dΩ1、dΩ2中同时被探测到的概率。
在DS3C 模型中,两个出射电子波函数用3 个两体库仑波函数的乘积表示,表达式如下[4-5]:

其中,库仑波函数由一个系数、一个伽玛函数、一个合流超几何函数连乘组成,形式如下:

系数αj(j=1,2,12)的具体表达式如下:
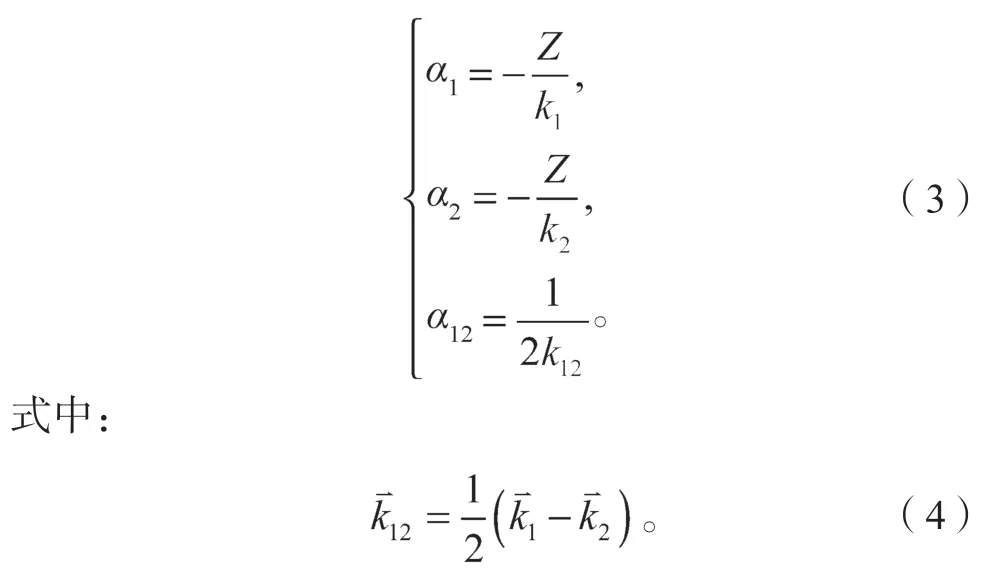
索末菲参数是模型修正的重点,比较经典的修正是从动量相关上得到的任意几何条件下的索末菲参量,表示如下[4-5]:
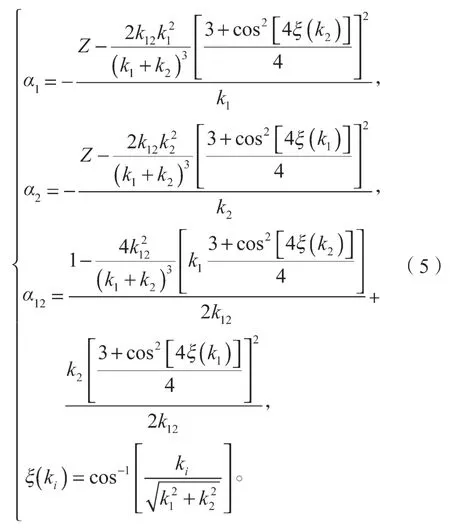
需指出的是,从反应过程上说原子中残留的电子并不能完全屏蔽原子核的电荷。DS3C 模型中忽略了实际散射过程中出射电子所感受到的残留电荷并不是1。针对以上情况,本文继续对该模型进行修正,并通过引入3 种修正有效电荷的方案来研究电离过程中TDCS 的变化规律。这些修改方案虽存在于文献中[6-8],却未能运用到特殊几何学安排条件下。本文将其引入动量依赖几何条件下,将式(5)中Z换为Z*。
第一个方案是由实验数据拟合得到的有效电荷[6],具体表达式为
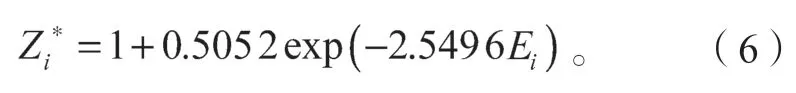
式中Ei(i=1,2)为反应后两个出射电子的能量。
第二个方案[7]:
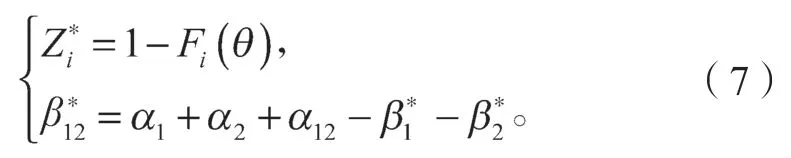
式中Fi(θ)为第i个出射电子感受到He+中残留电子对核的屏蔽函数,其表达式如下:
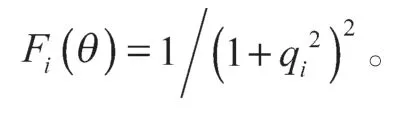
第三个方案采用量子力学课本中提出的形状因子,考虑残留电子的屏蔽效应[8],其表达式为
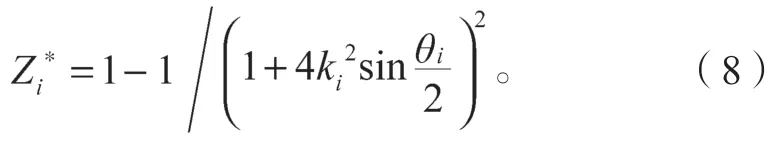
式中:ki(i=1,2)为两电子出射的动量;θi为第i个出射电子对入射方向的张角。
3 结果与讨论
本研究共考虑3 种残留电子屏蔽效应,并修改了DS3C 模型,参考实验几何条件,固定入射电子能量Ei=150 eV,敲出电子能量Eb=34.5 eV,敲出电子角θb为75°,90°,-105°时,计算了散射角θa在-40°~40°之间He 原子(e,2e)反应的TDCS。理论和实验结果见图1,其中DS3C 曲线摘自文献[4]。由于实验是相对测量,因此,本文所得结果在θa=-18°时进行了归一化处理。
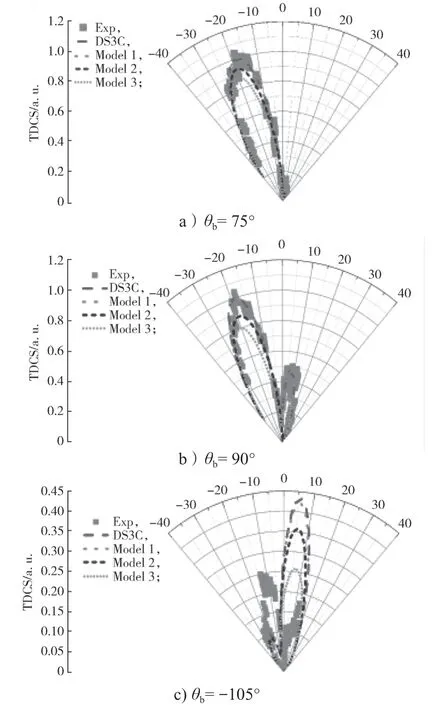
图1 Ei=150 eV,Eb=34.5 eV 时,电子电离He 原子的TDCS 随θa 的变化曲线Fig.1 TDCS curves of electron ionized He atoms changing with θa when Ei=150 eV,Eb=34.5 eV
从图1 的曲线形状看,图1 中所有的理论结果均呈现双峰结构,这与实验数据变化趋势符合。为便于描述,一般把θa<0°的峰称为前峰,θa>0°的峰称为后峰。可看到前峰相对高而宽,后峰相对低而平缓。随着散射角增大,前峰高度逐渐降低,后峰幅度增大。图1 中,DS3C 及3 种残留电子屏蔽模型均符合实验测量结果。就峰的相对高度而言,DS3C 与实验数据间的吻合度较高。考虑残留电子屏蔽效应的模型一与DS3C 结果几乎重合,这是因为模型一来源于实验拟合。模型二与三在散射角θa=0°附近即谷位置更符合实验测量结果,但对前峰修正却偏离了实验结果。当θb=90°时,DS3C 模型与实验数据吻合较好。考虑残留电子屏蔽效应的模型二降低了后峰,这与实验数据不符。模型三则统一降低了两峰高度。值得说明的是,模型三在θa<25°部分的修正比较成功,理论结果几乎与实验数据重合。当θb=-105°,所有曲线在峰的相对高度上均与实验数据有较大偏差,表现在前峰低而后峰和中间谷高于实验数据。在θa低于-20°和高于20°区域,理论和实验数据吻合得最好。
对于峰角分布,由图1 可知,θb=75°和90°时,DS3C 曲线符合实验测量结果,考虑残留电子屏蔽效应的模型一与DS3C 曲线基本重合。θb=-105°时,所有曲线峰和谷位置都向左偏移10°左右,导致实验出现谷位置,理论却呈现出峰结构。实验数据中两峰较明显,而理论预测后峰远比前峰高,前峰位置几乎不能分辨。
进一步探讨残留电子屏蔽效应对所得截面的影响。入射电子能Ei=150 eV,敲出电子角θb=72°,敲出电子能量分别为17.5,34.5,65.0,92.0 eV 时,He 原子(e,2e)反应DS3C 模型及3 种考虑残留电子屏蔽模型的TDCS 随θa的变化情况如图2 所示。
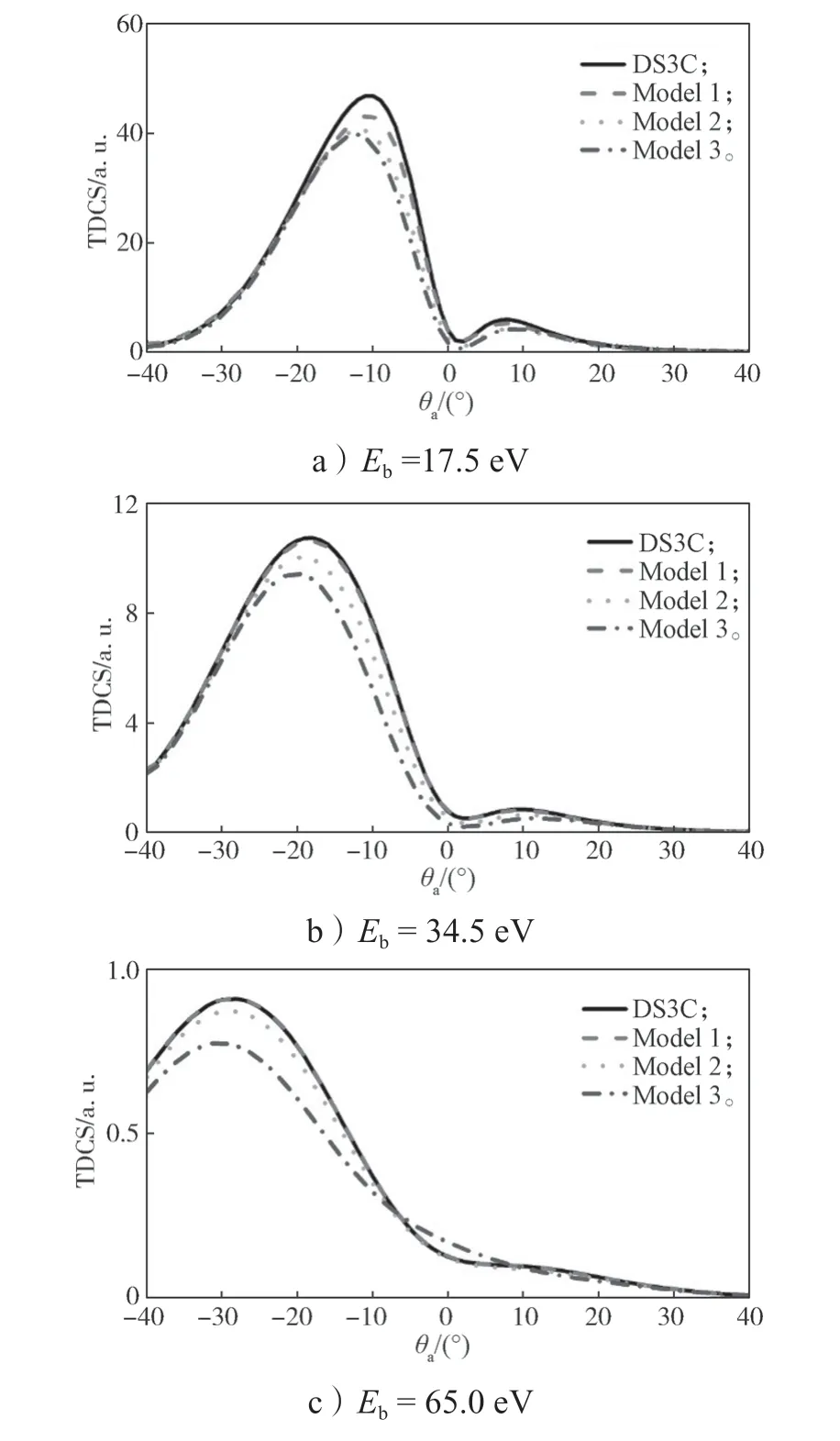
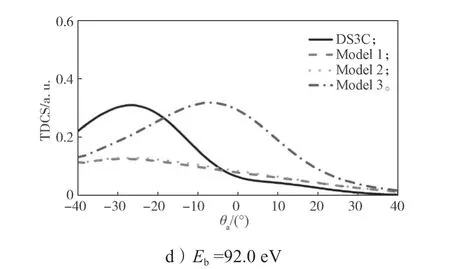
图2 Ei=150 eV,θb=72°时,考虑残留电子屏蔽效应后的电子碰撞电离He 原子TDCS 随θa 的变化曲线Fig.2 TDCS curves of He atoms ionized by electron impact changing with θa with the residual electron shielding effect taken into consideration when Ei=150 eV,θb=72°
观察图2 可知,随着角度增加,峰的高度不断下降、宽度增加、角分布的位置不断左移。当敲出电子能量固定在17.5 eV 时,4 种曲线在截面形状上近乎一致,差别仅体现在峰的相对高度。模型一的前峰和后峰高度有所下降,峰变窄,但峰位置几乎没变。在中间谷处和散射角小于-20°和大于20°的区域,曲线几乎重合。模型二的修正表现在前峰位置向左侧偏移,同样,前峰和后峰高度降低,谷的高度有一定程度下降。模型三变化趋势与前两种模型基本一致,但幅度更小。随着敲出电子能量增大到34.5 eV 时,模型一的修正曲线与DS3C 曲线基本重合。模型二和模型三降低了峰的幅度,峰宽变窄,且向左侧收缩。敲出电子能量为65 eV 时,DS3C 和模型一的曲线重合,模型二前峰幅度降低,模型三曲线后峰消失。相对于DS3C 曲线,模型三前峰高度有所下降。当敲出电子能量增加到92 eV 时,4 种理论的后峰均消失。DS3C 在后峰的位置有小的浮动,而模型一和二所得结果重合,模型三前峰位置向右移动,高度较DS3C理论值几乎没有改变。
固定敲出电子能量Eb=34.5 eV,敲出电子角θb=70°,入射电子能量Ei为95,150,260,480 eV 时TDCS 随θa的变化趋势如图3 所示。
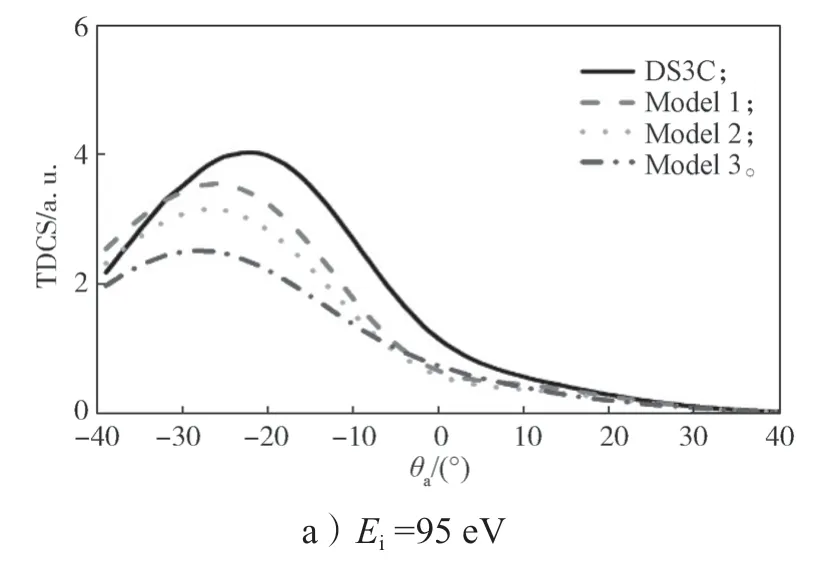
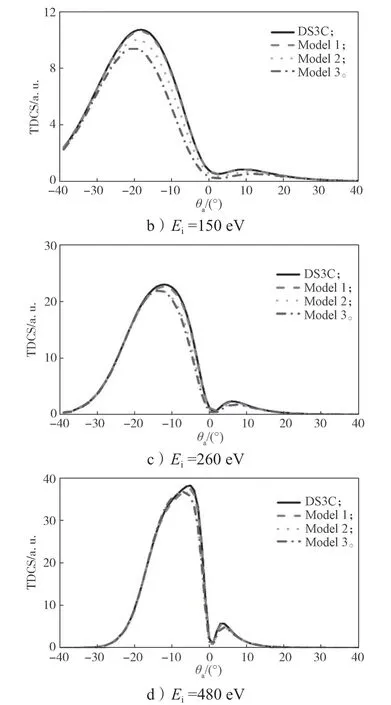
图3 θb=70°,Eb=34.5 eV 时,考虑残留电子屏蔽效应后的电子碰撞电离He 原子TDCS 随θa 变化曲线Fig.3 TDCS curves of He atoms ionized by electron impact changing with θa with the residual electron shielding effect taken into consideration when θb=70°,Eb=34.5 eV
由图3 可知,从整体上看,随着入射能量的增大,前峰高度增加,后峰逐渐突出,两峰的位置向θa=0°处靠近。3 种模型修正效果均不明显。这是因为随着入射能量增大,散射和敲出电子的能量均较大,而能量对应于动量和速度,即电子出射速度非常快,其经过反应区域的时间非常短,电子几乎感受不到核势影响。当入射电子能量为95 eV,DS3C 曲线没有后峰,前峰的位置为-25°~-20°。模型一前峰的位置向左偏移了5°左右,同时高度降低;模型二和模型三的修正效果基本一致,体现为降低前峰高度,向左偏移前峰位置。随着入射能量增加到150 eV,后峰开始呈现,DS3C 模型和模型一曲线几乎重合;模型二和模型三的峰高均降低,不明显的后峰变得更加模糊。此外可以看到曲线前峰的位置向左偏移宽度缩小,但θa在-40°~-30°和30°~40°的范围,4种理论曲线几乎重合。最后,入射能增加到480 eV 时,4 种理论曲线完全重合。需要注意的是由于前后峰都向着θa=0°方向靠近,导致中间的谷变成了尖锐的极小谷,TDCS 截面在最低处接近0。
固定入射电子能量Ei=150 eV,敲出电子能量Eb=34.5 eV,敲出电子角θb为70°,90°,105°和145°时TDCS 随θa的变化情况如图4 所示。
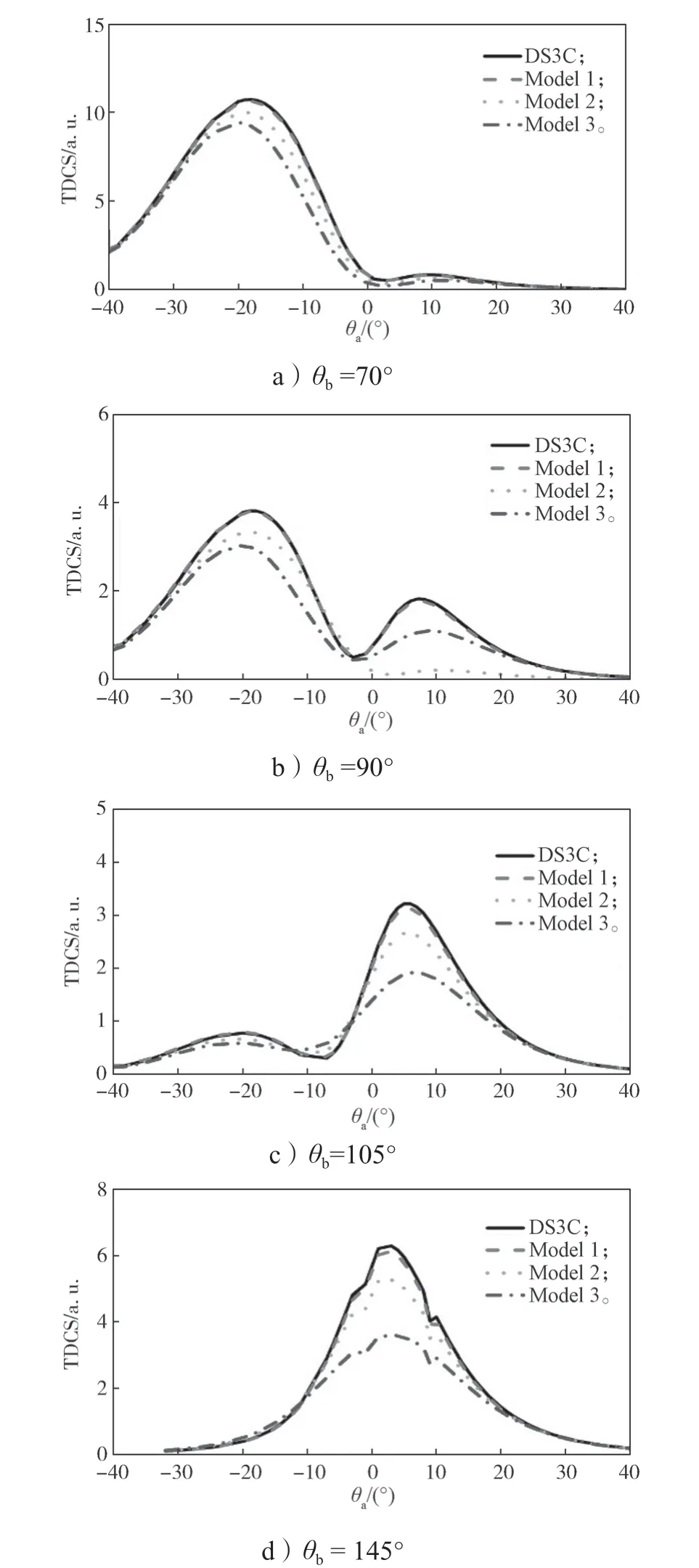
图4 Ei=150 eV,Eb=34.5 eV 时,考虑残留电子屏蔽效应后的电子碰撞电离He 原子TDCS 随θa 变化曲线Fig.4 TDCS curves of He atoms ionized by electron impact changing with θa with the residual electron shielding effect taken into consideration when Ei=150 eV,Eb=34.5 eV
由图4 可知。从整体上看,模型一与DS3C 模型几乎重合。4 种理论曲线都呈现相同的变化趋势,即前峰高度随θb增大而降低,后峰高度随θb增加而升高。当θb=70°时,4 种曲线的前峰均突出,后峰低矮不易察觉,模型二和模型三的修正都降低了前峰。当θb=90°时,曲线峰结构比较突出,模型三相较于DS3C 曲线结构相差不大,前峰和后峰下降。当θb=105°时,后峰强度超越前峰,在θa=-5°和10°附近,曲线向内凹陷,说明核对电子的作用越来越大,反应中残留电子屏蔽修正非常明显。
4 结论
本文修改了DS3C 模型,在截面依赖动量转移几何条件下对He 原子的TDCS 进行了理论计算,通过加入残留电子屏蔽理论,开展了DS3C 模型和3 种修正模型的对比研究,讨论了不同理论模型下残留电子屏蔽效应的影响。结果表明,残留电子屏蔽效应导致TDCS 在前散射区域幅度降低,而对后散射区域幅度的影响较小。这说明该效应在决定TDCS 方面起重要作用,在处理碰撞过程中应当予以考虑。通过对比截面的特征发现模型一修正效果最差,模型二和模型三修正效果明显,同时和实验数据之间的吻合程度进一步提高。本文揭示的物理效应有助于人们深入理解该几何条件下的微观碰撞过程,同时所得结果能为诸多领域的应用研究提供理论参考。

