文丘里管渐缩段影响限流性能试验与仿真
颜永丰,庞 飞,何 杰,刘 平
(1.江阴市节流装置厂有限公司,江苏 无锡 214405;2.湖南工业大学 科技学院,湖南 株洲 412007;3.江苏科技大学 土木工程与建筑学院,江苏 镇江 212100)
0 引言
随着国家能源紧张,核能受到广泛重视,与核工业相关的建筑和机械两大领域随之兴起。在核电厂、水利水电等大型工程中或者核安全级运行工况下,主给水流量的准确测量传统直接影响其运行稳定性和经济性,因此,节流装置凭借其高度可靠、应用成熟、有效限流等优势在流量测量领域占据重要地位[1-2]。以文丘里管为例,服役工作期间,受诸多专设系统的影响,设备装置需承受复杂多变的工况,管道前后压损会对流体动力产生影响[3],流量达临界条件时会发生空化反应,其产生的气相水泡会对管壁造成冲击、侵蚀[4-5],继而破坏管壁。
蔡守华等[6]通过对偏心文丘里管进行实际测流试验与FLOW-3D 数值模拟对比研究,发现偏心文丘里流量计流出系数的相对误差小于5%;文丘里扩散段不同,扩散角度会对流体速度和湍动能产生不同性质的分布影响[7];由于湍流理论和空化反应与流体的不稳定性和结构间相互作用有复杂关系,J.Decaix等[8]对沿文丘里管几何形状发展的气穴反应进行了数值研究,构建了新比例自适应模型与分离涡流仿真;A.Peters 等[9]在微射流理论基础上,采用一种新的空化模型对研究对象进行模拟、预测,证明了数值计算结果可信,其最终模拟结果与试验结果展现的冲蚀面积较吻合;考虑水中空气演化的时变性,刘馥瑜[10]采用计算流体动力学方法对文丘里管水力装置空化特性及机制做了不同参数研究,为之后的装置设计优化提供参考;随着空化程度增强,汽云的崩溃会使尾迹区湍流脉动增强,同时也会改变涡的伸展[11-12];D.A.Wilson 等[13]研究了管道几何扩散角度和喉长喉径比值对空化气泡尺寸的影响,发现影响较小。在分析以上研究成果的基础上,得知目前文丘里管渐缩段位置几何尺寸对管内流动情况及参数的影响研究较少,而渐缩段形状与尺寸却是影响限流装置极为重要的控制参数之一。
综上所述,本文拟以渐缩段位置3 种结构形式的限流文丘里管作为研究对象,基于ANSYS Workbench 和Fluent 对正常补水和临界限流工况下文丘里管内部流体性能进行数值仿真,分析压强及流量参数计算值与试验值间的误差。判断数值计算结果、数值方法的正确性以及所设计文丘里管在临界条件下能否成功限流在设计值39.8 m3/h 以下,研究流体域有关参数分布情况,并优化文丘里管渐缩段结构形式,提高管道内部性能,以期可推广至具体应用。
1 计算模型
1.1 模型简介
本文中3 种限流文丘里管为江阴市节流装置厂有限公司设计并生产,该装置应用在满足科研目标的CAP1400 核电厂CVS 化容系统。3 种结构形式文丘里管的管径、渐扩段、入口及出口几何形状均相同,区别在于渐缩段位置,分别为弧形弯曲一次、弧形弯曲两次和传统直线型3 种结构形式。详细几何尺寸如图1 所示(单位为mm)。下文均用一号、二号、三号管号分别代表文丘里管渐缩段为弧形弯曲一次、弧形弯曲两次、传统直线型3 种几何形状。
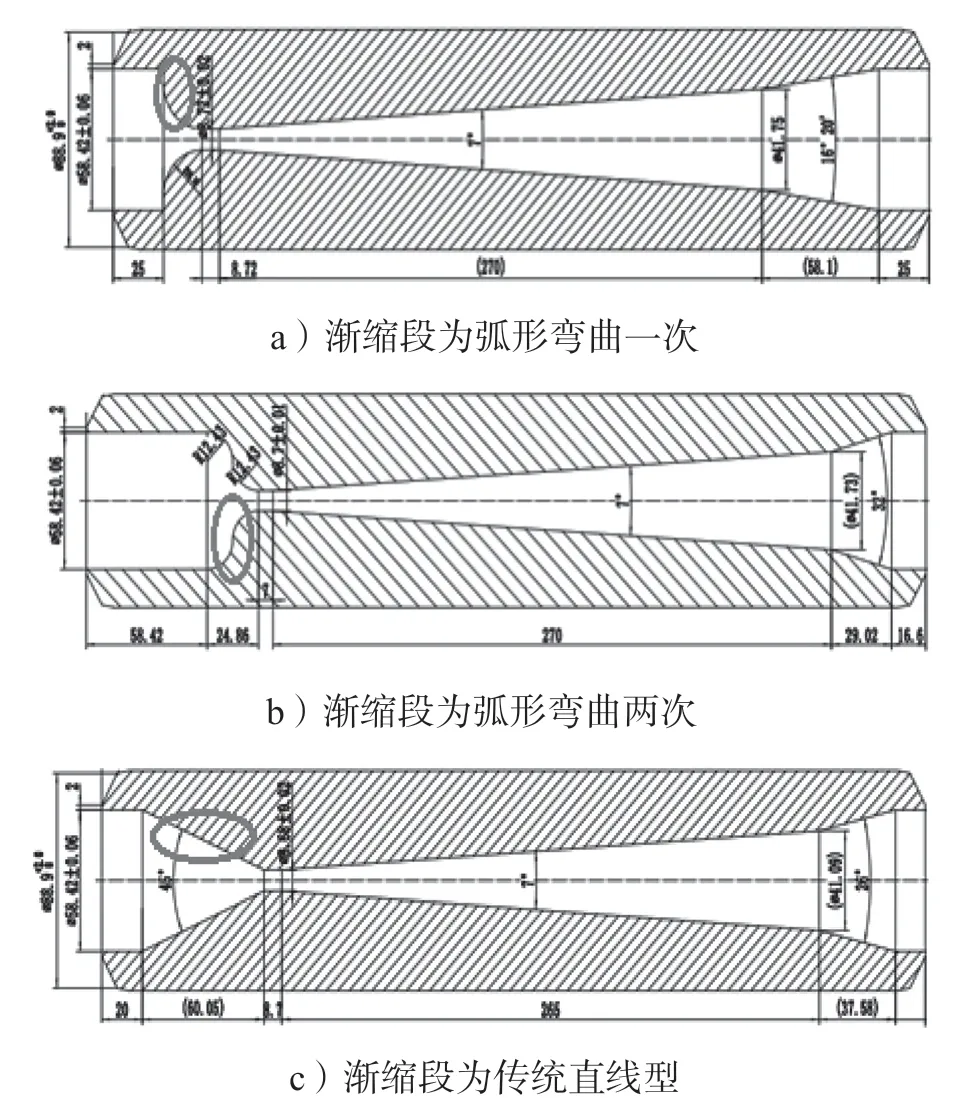
图1 限流文丘里管几何示意图Fig.1 Geometric sketch of current limiting Venturi tube
1.2 有限元模型及网格
研究对象计算的前处理在ANSYS Workbench 中进行,由于研究内容为限流文丘里管管道内部流体性能,故本文利用Fluent 模块取文丘里管流体域进行分析。流体域模型为旋转轴对称结构,考虑到计算内容、计算资源等方面原因,本文基于二维平面建模,取流体域截面的1/2 进行计算分析,模型全部位于X轴与Y轴的正区域内,详见图2。对于2D 面体,采用四边形单元主导的网格划分方法,采用Inflation 膨胀控制处理边界层,使其向内部网格平滑过渡。生成的CFD 网格如图2 所示。

图2 流体域模型网格划分图Fig.2 Fluid domain model grid division diagram
确定具体网格尺寸之前,先对模型尝试性进行不同尺寸的网格划分,拟定1.5,1.0,0.5,0.3,0.2,0.1 mm 5 种网格尺寸。结构总弹性能见图3a。
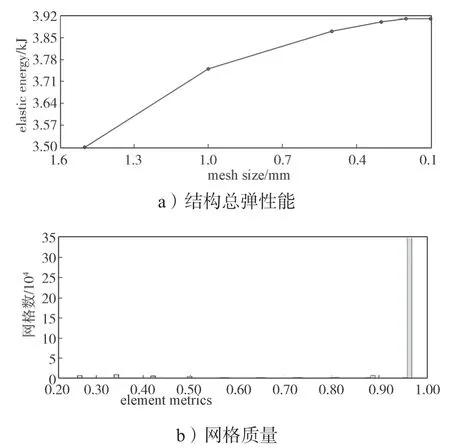
图3 结构总弹性能与网格质量Fig.3 Structural elastic energy with its grid quality
从图3 中可以看出,结构总弹性能在0.3 mm 尺寸后基本相同。权衡计算时间与精度,计算取0.3 mm网格尺寸。此外,0.3 mm 网格质量见图3b,由图可知网格质量达0.95 以上,故计算结构精度较有保障。
由于网格划分过密,在图中不便全部显示,因此部分入口及出口未截图。网格划分之后,网格质量在0.95 以上,可认为网格质量很好。
1.3 边界条件
有限元模型计算中,最重要的是确定边界条件,本文限流文丘里管节流装置流体域稳态性能数值分析过程中,将流体入口位置定义为入口边界,出口位置定义为出口边界,壁面定义为wall,流体域截面对称轴定义为axis。边界条件如图4 所示。
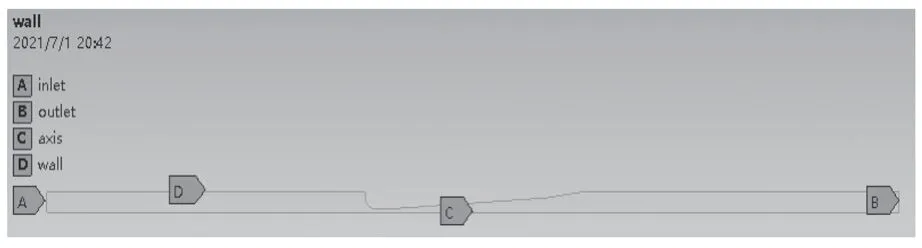
图4 边界条件示意图Fig.4 Boundary condition schematic diagram
1.4 计算流程
基于ANSYS Workbench 19.0 软件,湍流模型选用Realizablek-ε方程模型,空化模型选用适用于气泡流的混合多相流模型[14];由于考虑了流体温度,在计算中加入Energy 能量方程;Materials 模块指定流体域对应材料,使用液相水water liquid,限流工况考虑water vapor;设置计算边界时,入口边界条件选用pressure inlet,出口边界条件选用mass flow outlet,限流工况则选用pressure outlet;最后,设置变量残差监视参数并进行初始化,进行迭代求解计算。数值模拟计算流程图如图5 所示。
2 试验方法与结果
2.1 流量方程
管道内流体的流量受喉部直径及进出口压强的影响,其余影响参数为流体系数。流量方程如公式(1)所示:
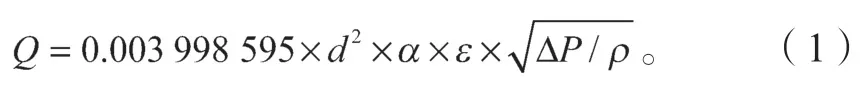
式中:Q为流量,m3/h;d为喉部直径,mm;α为流量系数,为试验介质可膨胀系数,对于试验中介质水,取α=1.0;ρ为试验介质密度,kg/m3;ΔP为压差,Pa,且ΔP=K1×Δω,其中K1为系数,对同一个节流装置而言基本为一个常数;Δω为压损,Pa,Δω=P1-P2;P1为入口压强,MPa;P2为出口压强,MPa。
2.2 试验过程
本文试验对象为限流文丘里管流量元件,管道尺寸Φ89 mm×16 mm,共有3 种渐缩段结构形式。试验样机与正式产品完全相同,在生产车间制造完成后开始试验。试验工况分为正常运行工况及限流工况。
本次试验装备为自制,所需设备及型号包括:电动机(型号为YKS800-4,可调速)、给水泵(型号为FT7U32M,最大出口压强为25 MPa,最大流量为581 m3/h)、压力变送器(型号为E+H PMP71,量程为0~40 MPa,精度等级为0.5)、孔板流量计(型号为LGPH-15G-15B-QY10G-O1-F1IP,量程为0~260 m3/h,精度等级为0.5,压差范围为0~100 kPa;型号LGPH-08G-26B-QY10G-O1-F1IP,量程0~50 m3/h,精度等级为0.5,压差范围为0~100 kPa)。试验布置简图如图6 所示,布置图做了一定简化,只保留主要设备,图中箭头为水流方向。
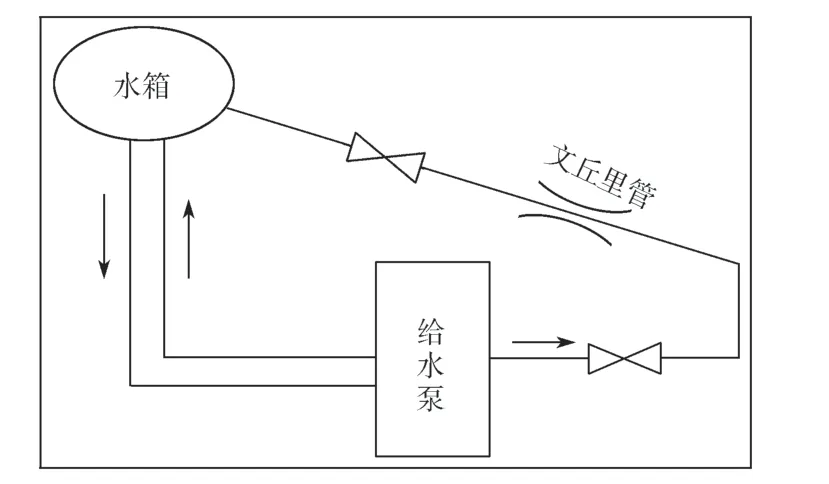
图6 试验布置简图Fig.6 Test layout diagram
对于正常运行工况的性能试验,正常补水时,同时调节电机转速、主系统出口阀门开度以及旁路阀门开度,使管道入口流量达到工况目标值,保持管道入口压强为指定值,在试样工件前后测压位置记录此时流体的压强等相关数据,用以计算压强损失。
对于限流工况下的性能试验,启动水泵,待出口压强稳定后打开闸阀,同时调节电机转速、主系统出口阀门开度,以及旁路阀门开度至管道入口压强为工况目标值,记录此时的最大流量,此时管道达到临界状态,再逐渐提高流量至目标值,记录出口压强等数据。试验过程中记录部分现场照片如图7 所示。

图7 限流文丘里管试验现场照片Fig.7 Physical pictures of current limiting Venturi test
2.3 试验结果
对于每种管道,正常补水工况进行了两次试验,限流工况进行了一次试验,根据现场数据记录,本节列出限流文丘里流量元件试验结果如表1 所示(用一号、二号、三号分别代表文丘里管渐缩段为弧形弯曲一次、弧形弯曲两次、传统直线型等几何形状)。
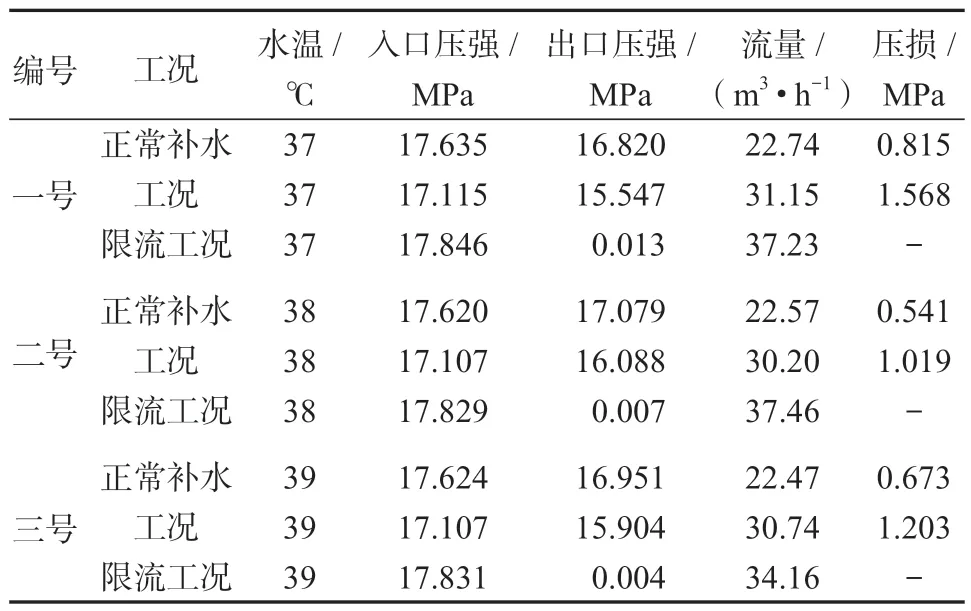
表1 文丘里管试验结果Table 1 Venturi test results
表1 结果说明3 种限流文丘里管在各工况下的水温、入口压强及流量在设计过程中相同,但实际试验时数值略有误差,本文中忽略该试验误差。
3 计算结果
在Fluent 的后处理CFD-Post 模块中查看计算结果,主要观察文丘里管流体域压强分布、流速、流量、入口及出口压强、空化情况等参数性质细计算结果。
3.1 流体域性能分布
从下文计算值与试验值的误差来看,第一次正常补水工况结果要优于第二次,故本小节只列出第一次正常补水工况后处理结果。
3.1.1 流速分布
图8 所示为限流文丘里管流速分布情况。

图8 限流文丘里管流速分布情况Fig.8 Velocity distribution of current limiting Venturi tube
如图8 所示,3 种类型文丘里管的流场速度分布基本类似。在渐缩段位置,由于截面急剧减小,管道中流体速度开始增大,至喉部位置流速到达峰值;在渐扩段位置流速又逐渐下降,至出口位置稳定不变,恢复正常。
图9 为文丘里管中流体速度与管纵向位置曲线。

图9 限流文丘里管中流体流速曲线Fig.9 Velocity curves of current limiting Venturi tube
从图9 可以看出,管道面积的急剧缩小是影响流场速度的关键因素,而气泡的产生对流场速度的影响较小。
3.1.2 压强分布
图10 所示为限流文丘里管压强分布情况。
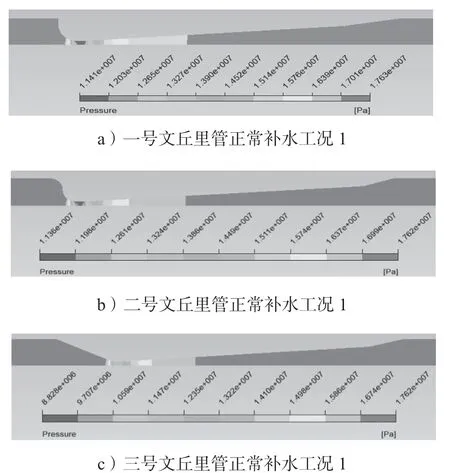
图10 限流文丘里管压强分布情况Fig.10 Pressure distribution of current limiting Venturi tube
如图10 所示,3 种类型文丘里管的压强分布情况基本类似,仅三号文丘里管的压强分布略微较小。在渐缩段位置处,由于截面急剧减小,管道中压强开始变小,至喉部位置压强值最小;在渐扩段位置压强开始增大,至出口位置稳定不变,恢复正常。
图11 为限流文丘里管流体域压强曲线。如图11所示,正常补水工况下,流体流经喉部位置时流场的压强迅速下降,至渐扩段位置时压强逐渐上升,而后至出口位置稳定不变,而且分布规律与曲线图较为吻合。
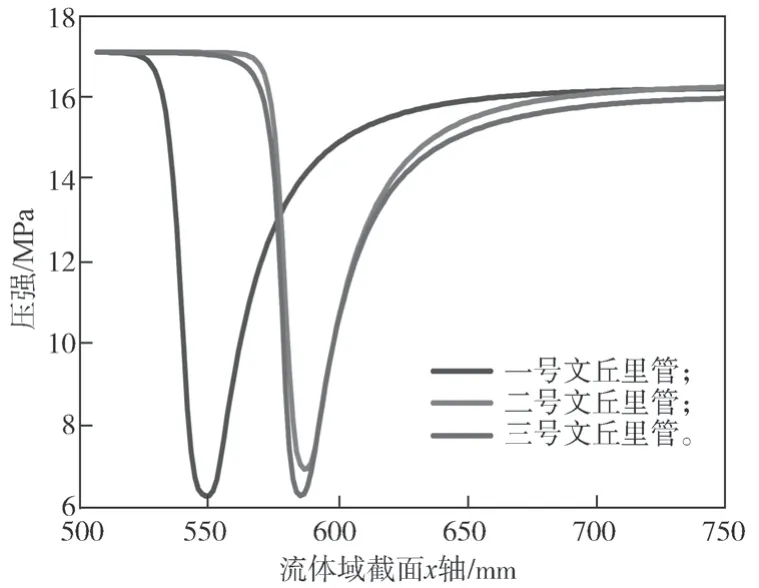
图11 限流文丘里管流体域压强曲线Fig.11 Fluid domain pressure curves of current limiting Venturi tube
3.2 汽含率分布
限流工况在Fluent 中计算后导出流体域气体体积分布结果,如图12 所示。
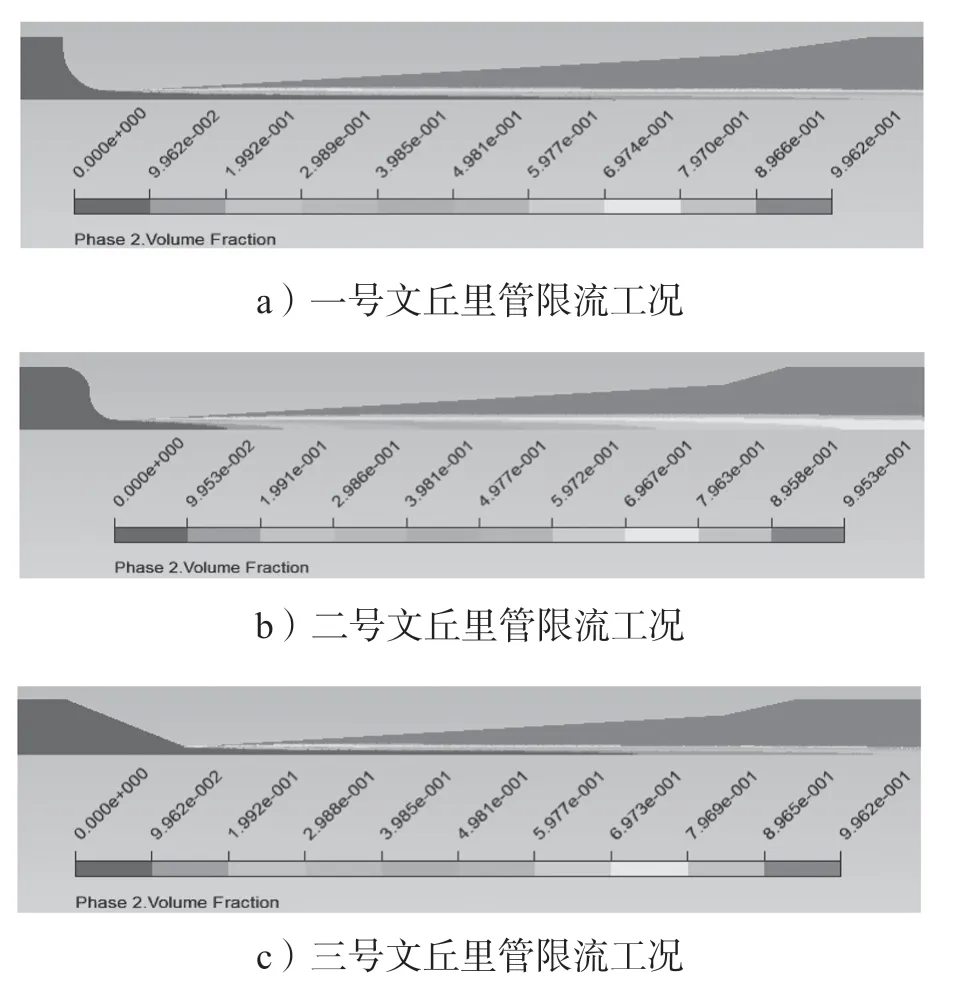
图12 文丘里管流体域汽含率分布情况Fig.12 Vapor distribution in fluid domain of Venturi tube
如图12 所示,该工况下,流体域前后压差巨大,导致喉部发生空化反应,图中喉部位置先开始发生空化,而后向后延伸。
空化部分主要集中于渐扩段及之后的区域,如图13 所示。
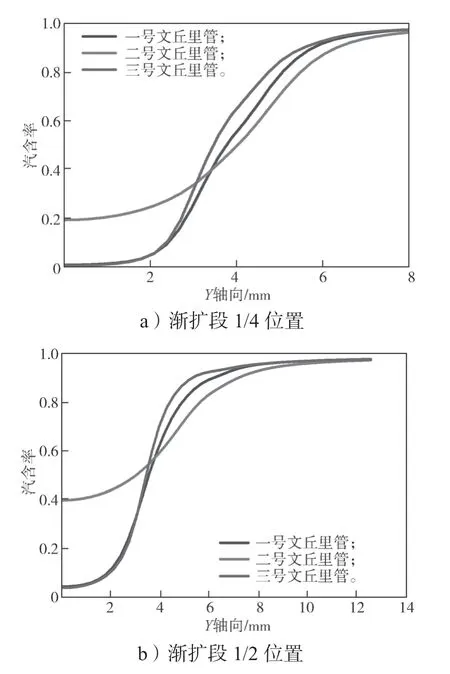
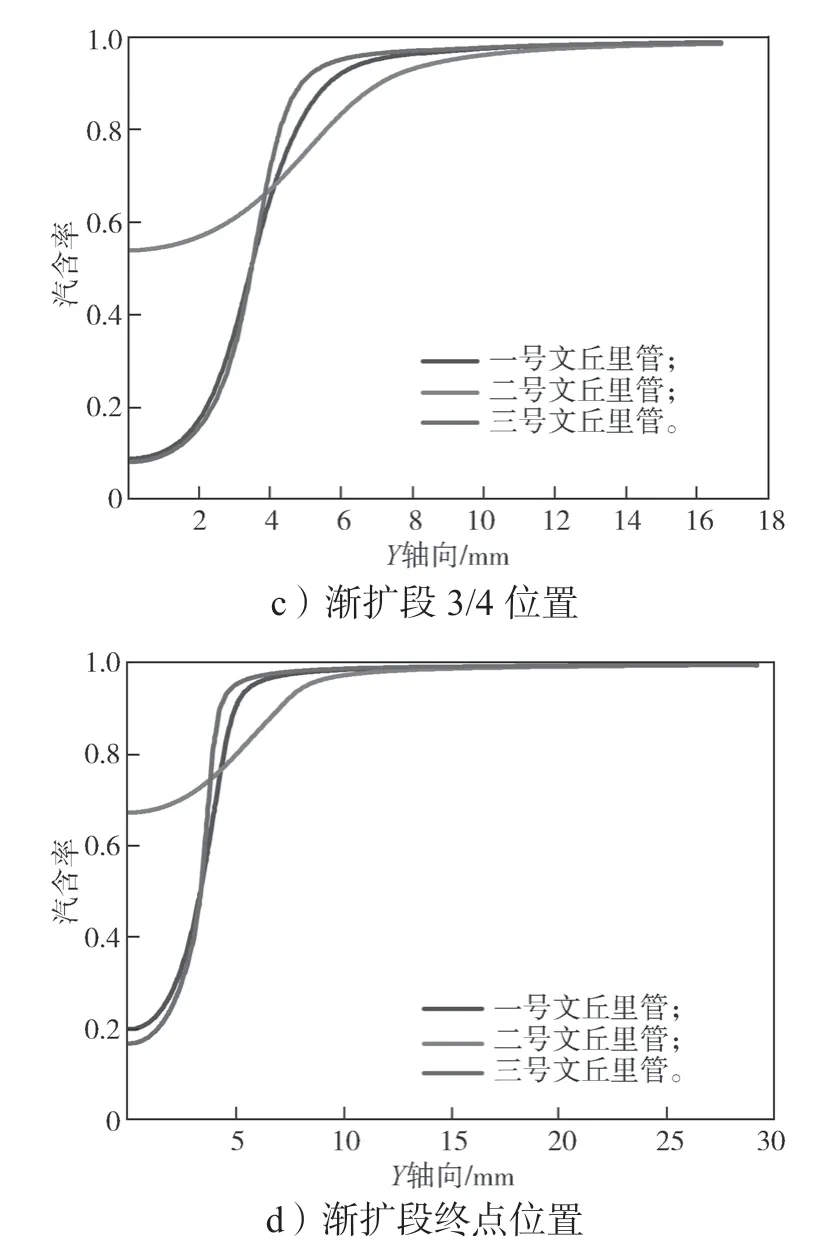
图13 渐扩段不同位置管径方向汽含率曲线Fig.13 Vapour ratio curves of pipe diameter direction at different positions of Vunturi tubes
由图13a~d 所示渐扩段1/4 处、1/2 处、3/4 处及渐扩段终点处在管径方向上的气体体积分布曲线,一号和三号文丘里管曲线较接近,二号文丘里管在横坐标初始位置高于另外两者,总体上,二号文丘里管的空化反应比另外两者更充分、均衡。
3.3 计算误差
基于数值模拟方法,将流体参数的计算值与试验值进行对比,通过数据误差分析数值计算结果的准确性,如表2 所示。

表2 文丘里管工况计算结果Table 2 Working condition calculation results of venturi tube
根据表2 列出的计算结果可知:第一次正常补水工况下,3 种文丘里管出口压强计算值与试验值的误差分别为2.0%,0.5%,0.5%;第二次正常补水工况下,3 种文丘里管出口压强计算值与试验值的误差分别为4.6%,1.5%,1.0%;限流工况下,3 种文丘里管流量计算值与试验值的误差分别为4.7%,3.2%,0.9%。
4 讨论
正常补水工况的出口压强计算值与试验值较吻合,误差很小,均在5%以内,可认为数值仿真模型所得结果是可信的[15]。另外,临界限流工况下计算流量与试验流量也较吻合,误差较小,且均小于设计目标39.8 m3/h,3 种文丘里管在临界工况下均能成功限流。就流量实测试验而言,二号文丘里管的限流情况优于一号文丘里管,三号文丘里管最劣,比较依据为二号文丘里管流量数值更接近39.8 m3/h。
在压强曲线图11 中,二号文丘里管出口位置的压强略高于一号文丘里管、高于三号文丘里管,在入口压强大致相当的情况下,即二号文丘里管前后压损略小于一号文丘里管、小于三号文丘里管(第一次正常补水工况下,3 种文丘里管前后压损分别为0.48,0.45,0.579 MPa;第二次正常补水工况下,3 种文丘里管前后压损分别为0.853,0.774,1.047 MPa)。由此可推断,在管道其余部位几何形状都相同的情况下,文丘里管渐缩段为弧形弯曲两次所致流体域性能以及对压强的损耗情况均优于渐缩段弧形弯曲一次的,而渐缩段为传统直线型的性能最差。
根据伯努利方程,可知

式中:Q为流量,m3/h;A为管道截面积,m2;r为管道内半径,mm。
本文文丘里管水平放置,故有式(3):

式中:ρ为试验介质密度,kg/m3;v0为初始速度,m/s;p0为初始压强,MPa;C为常数。

式中:Δp为压差,MPa;cp为压强损失系数。
表3 为文丘里管压强损失系数结果。
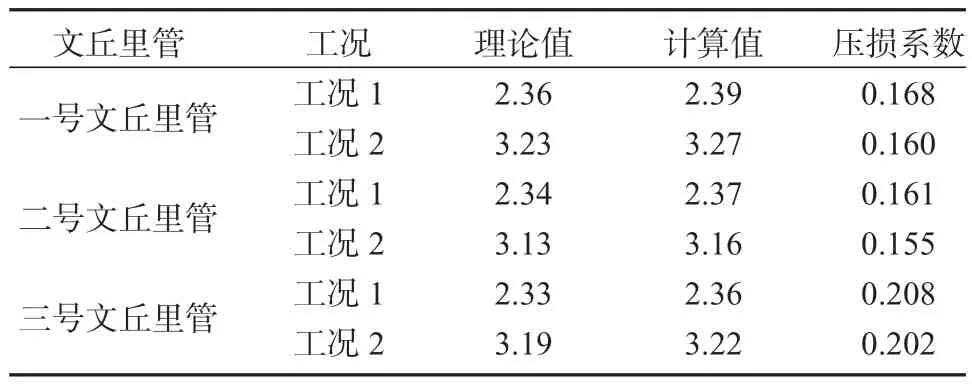
表3 文丘里管压强损失系数结果Table 3 Pressure loss coefficient results of Venturi tube m/s
由表3 的结果可知,对于变内径管道,若流量恒定,管径与流速成反比,管径与水压强成正比。对于本文3 种渐缩段结构形式的文丘里,压强损失系数亦可反映管道设计性能,计算结果及统计数据见表3。同一管道,两种工况所得压强损失系数大致接近,各管道压强损失与流体初速度无明显关系。压强损失系数数值从小到大依次为二号文丘里管、一号文丘里管、三号文丘里管,证实了二号文丘里管设计的管道性能最优,其以较小的压强损失进行工作,而三号文丘里管设计性能最差。
5 结论
综上所述,通过对渐缩段位置3 种结构形式的限流文丘里管进行试验和数值仿真计算,将正常补水和临界限流工况的计算值与试验值对比,分析误差,判断数值计算结果、数值方法的正确性,以及流体域有关参数的性能分布,得出以下结论:
1)从压强性能和压强损失系数来看,管道其余部位几何形状都相同时,限流文丘里管渐缩段为弧形弯曲两次的压损性能优于渐缩段弧形弯曲一次,压损值约为弯曲一次形状的90%,渐缩段为传统直线型的性能最差。
2)在汽含率方面,渐缩段为弧形弯曲两次的文丘里管空化反应比另外两者更充分、更均衡,相较于渐缩段前后产生折线变化的几何形式,弧形均匀平滑过渡的内部结构有利于改善管道流体性能,更好地发挥其限流作用。
3)同一类型管道,在不同工况下,压强损失系数基本相同。压强损失系数数值从小到大依次为二号、一号、三号文丘里管的损失系数,证实了二号文丘里管设计的管道性能最优。

