含内生变量的高维部分线性模型特征筛选

陈海燕，赵培信,

（1.重庆工商大学 数学与统计学院，重庆 400067；2.经济社会应用统计重庆市重点实验室，重庆 400067）

0 引言

部分线性模型[1]同时含有参数分量和非参数分量，在对实际问题建模过程中兼具经典参数模型和非参数模型的优点，目前已被广泛地应用于社会科学、计量经济学以及生物医学等领域。另外，随着现代数据收集技术的不断发展，研究者们能够在科学研究的各个领域以较低成本收集到大量的高维数据。这种大数据的统计推断过程中，往往会遇到超高维情况，即数据的维数远远大于样本量，从而导致经典的统计推断理论将无法直接应用。

目前关于超高维数据的统计推断问题，一般是先利用一些变量筛选方法，从大量的数据中筛选出一些重要变量，然后基于所筛选出的重要变量进行统计建模。关于超高维数据下部分线性模型的变量筛选问题，杨宜平等[2]结合样条方法和Dantzig 或Lasso 进行变量选择和未知参数估计。赖秋楠等[3]将超高维部分线性模型转化为高维线性模型，考虑了协变量间的相关性，提出了profile贪婪向前回归变量筛选方法。杨鑫等[4]基于profile 最小二乘方法和保留正则化方法，提出了新的变量选择方法。但是这些文献均是在假定超高维数据为外生协变量的情况下进行讨论的。Fan J.Q.[5]、Lin W.[6]等指出，在超高维模型中存在许多可能导致违反外生性假定的因素，例如选择偏差、测量误差和遗漏变量等。因此对超高维数据统计建模过程中假定所有变量均为外生协变量是具有限制性且往往是不现实的。在违反外生性假设时，现有的基于边际特征筛选方法可能会筛选出那些隐藏的重要变量，并产生较多的假阳性重要变量。

目前，关于超高维内生性协变量的重要变量选择问题研究还不多。针对含内生协变量的超高维线性模型，Fan J.Q.等[5]通过构建惩罚聚焦广义矩法准则函数，有效实现了降维，并证明了模型存在内生性时，该方法也具有Oracle 性质。Lin W.等[6]提出了一个两阶段正则化框架，通过使用稀疏诱导惩罚函数，将经典的两阶段最小二乘法（two stage least square，2SLS）扩展到高维。Hu Q.Q.等[7]提出了一种新的特征筛选工具来衡量预测变量的边际效用，然后引入两阶段正则化框架来识别重要的预测变量。但是，对超高维内生性数据下部分线性模型的重要变量选择问题目前还没有相关研究。为此，本文在假定部分协变量为内生协变量的情况下，研究超高维部分线性模型的重要变量筛选问题。

具体地，结合工具变量调整技术，本文提出了一种新的重要变量筛选方法。理论上证明了所提出的筛选方法具有排序一致性。这意味着依据效用测度，总是可以大概率地将重要变量排在不重要变量之前，从而保证可以清晰地区分重要变量和不重要变量。

1 基于工具变量调整的重要变量筛选方法

本节中，假定模型中线性部分的维数p远远超过样本量n，且维数p随着样本量n呈指数型增长。本文考虑的部分线性模型结构如下：

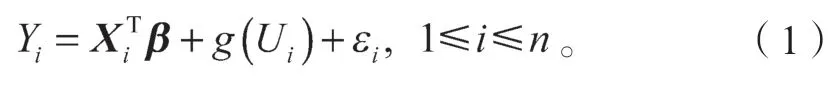
式中：Xi为p维协变量，且

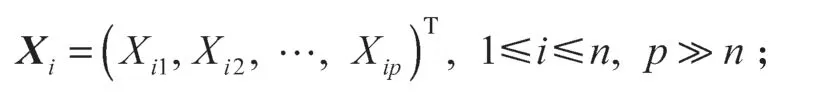
β为未知参数的p维向量，且

g(·)为未知的非参数函数；

Ui为一维变量；

εi为模型误差。

式中：Zi为对应的q维的工具变量向量，且

Γ为p×q维的未知参数矩阵，

e为模型误差，且e=(e1,e2,…,en)，其中ei=(ei1,ei2,…,eip)T，且满足

综上所述，考虑模型

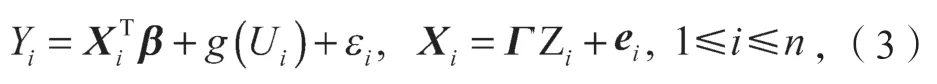
满足如下条件：

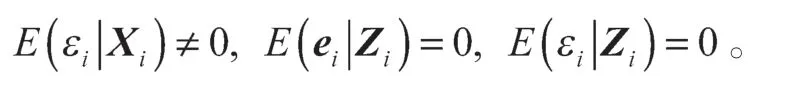
假设真参数β是稀疏的，即集合A={j:βj≠0,1≤j≤p}很小，则本文的目标是估计集合A。

经典的两阶段最小二乘（2SLS）[8]和两阶段正则化（two stage regularization，2SR）[6]将协变量替换为它们对工具变量的期望。更具体地说，变量首先在工具变量上回归，然后响应变量在变量第一阶段的预测结果上回归。然而，因为变量和工具变量的维度随着样本量呈指数增长，2SLS 方法和2SR 方法的性能分别面临众多工具变量的维度灾难和计算成本的问题。因此，需要探索新的方法来获取集合A。

注意：如果响应变量在工具变量上进行回归，根据上述模型（3），可以得到如下模型：

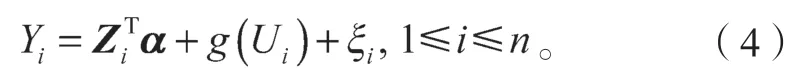
式中：α是q×1 维向量，且α=ΓTβ；

ξi为新误差，且ξi=+εi。

为了找到一个特征筛选工具来估计活跃集A，首先考虑一个例子。在模型（4）中，很容易得到：

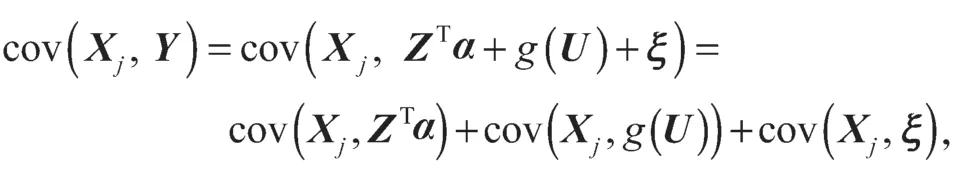
另一方面，

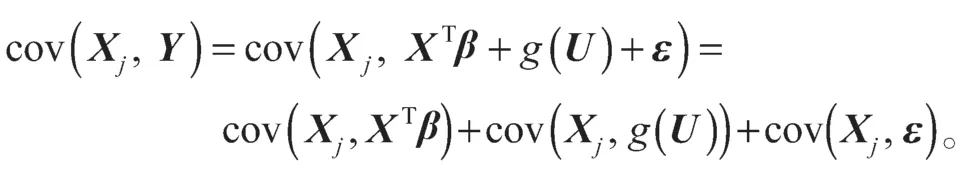
结合上面的方程，可以得到：

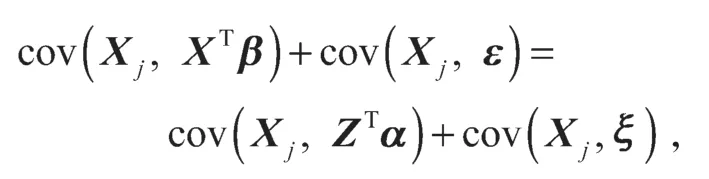
进一步展开，得到：

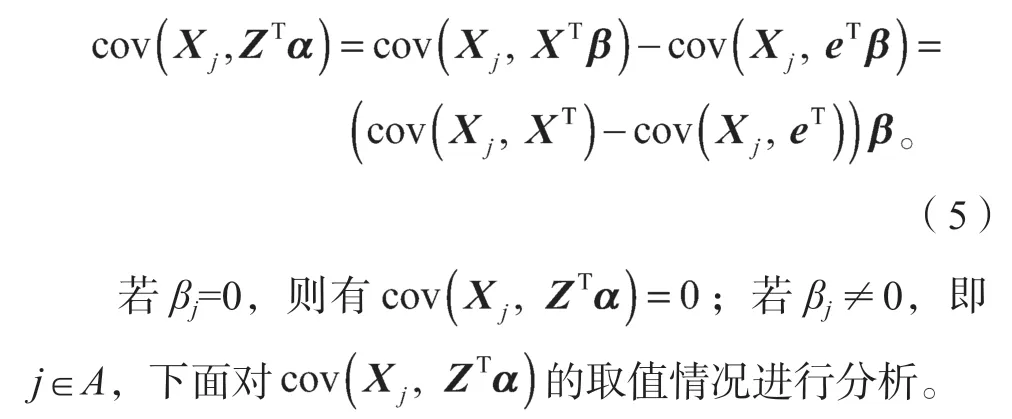
式（5）可表示成

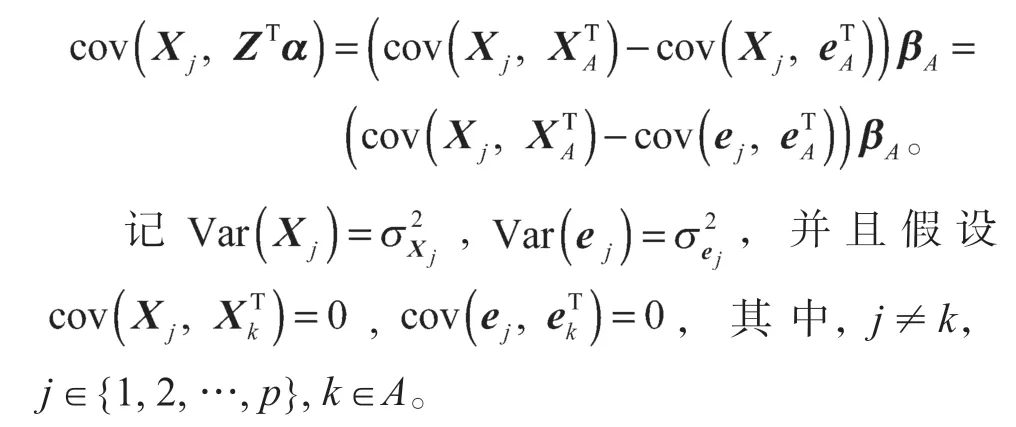
通过这些假设，可以得到如下结论：

结合上述分析，可以得到：

2 重要变量筛选迭代算法

根据部分线性模型的剖面估计思想，首先假定β已知，则模型（1）可被看作是一个非参数回归模型：

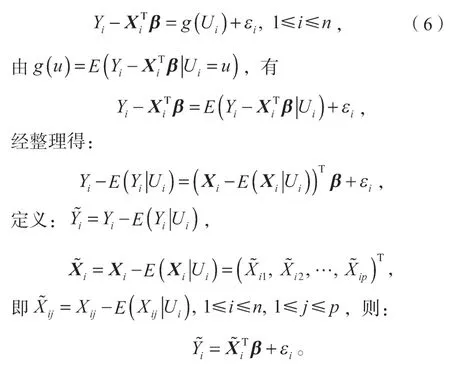
对于非参数g(u)可使用局部线性光滑方法构造其估计量，它能减少Nadaraya-Watson 核估计的偏差和Gasser-Müller 估计的方差，并能够避免核估计的边界效应，在边界点和内点有相同的收敛速度。设回归函数g(u)在u的邻域内有连续的一阶导数，如果Ui在u的一个小邻域内，可用一个线性函数局部地逼近回归函数g(Ui)，有：

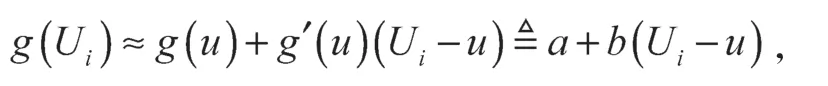
式中a、b为回归系数。

因为假定β已知，可通过极小化下式加权最小二乘目标函数求a和b，

式中：Kh(·)=K(·/h)/h，其中K(·)为核函数，h为窗宽，且h＞0。

接下来设计两阶段方法。

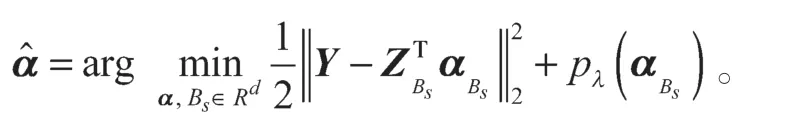
式中：pλ(·)为惩罚函数；λ为调和参数，且λ≥0。

值得注意的是，没有必要对解释非活跃预测变量的工具变量做出任何条件假设。因此，所有非活跃预测变量都可以使用一个工具变量，即使这个工具变量非常弱，这意味着虽然预测变量X是高维的，但工具变量Z并不需要是高维的。通常情况下，要求工具变量的数量应不小于用于识别的预测变量的数量，但是，系数的识别对筛选目标并不重要。即使系数不确定，仍然可以确定活动回归量。因此，当工具变量的维度不太高时，可以忽略第1 阶段的特征筛选。从理论上讲，当工具变量的维数小于样本量时，可以使用“普通最小二乘法”代替变量选择过程。

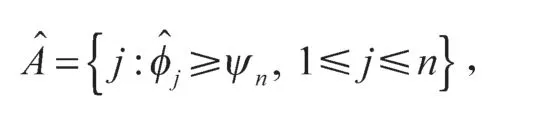
式中，ψn是给定的阈值参数。

值得注意的是，无论模型中是否存在内生协变量，本文所提出的筛选程序都是可行的。

3 理论结果

本节将讨论所提出的筛选程序的理论性质。下列条件是为了方便技术证明，尽管它们可能不是最弱的条件。

C1）随机误差e的条件。给定为

C2）协变量X的条件。给定为

C3）工具变量Z的条件。

C3-a）存在正常数K1、K2和κ，使得

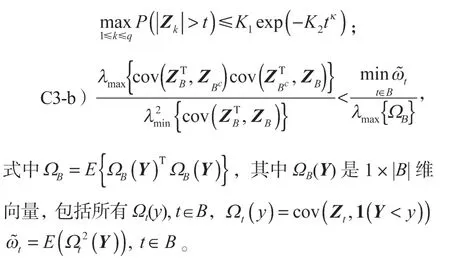
C3-c）线性条件为

C4）活跃集A和B之间的关系为

接下来，介绍所提出的筛选程序的理论性质，这些理论性质是新筛选方法的主要理论基础。

定理1在条件C1、C2、C4 下，有如下不等式关系成立：

4 定理证明

定理1的证明 基于模型（3）和模型（4），设为真系数，可以得到：

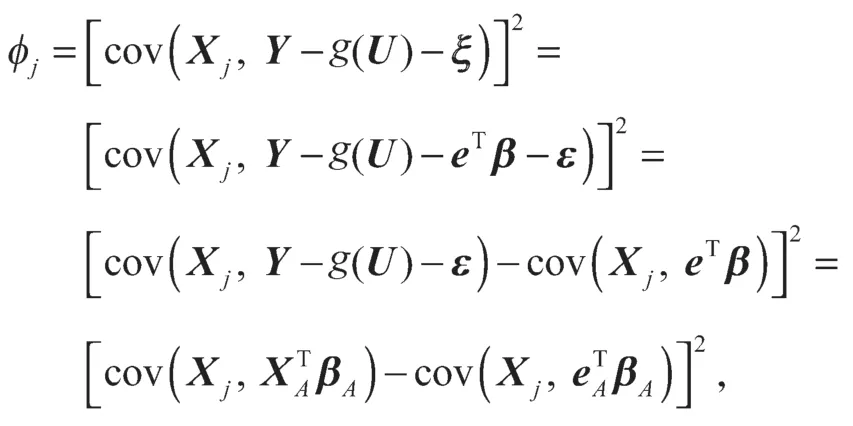
式中：βA由所有的βj，j∈A组成；由所有的∈A组成。

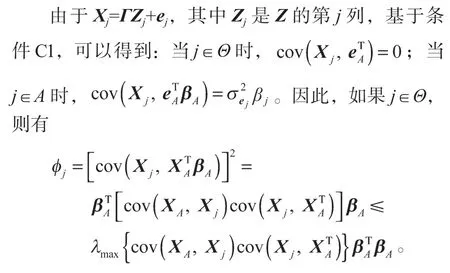
另一方面，如果j∈A，可以得到：

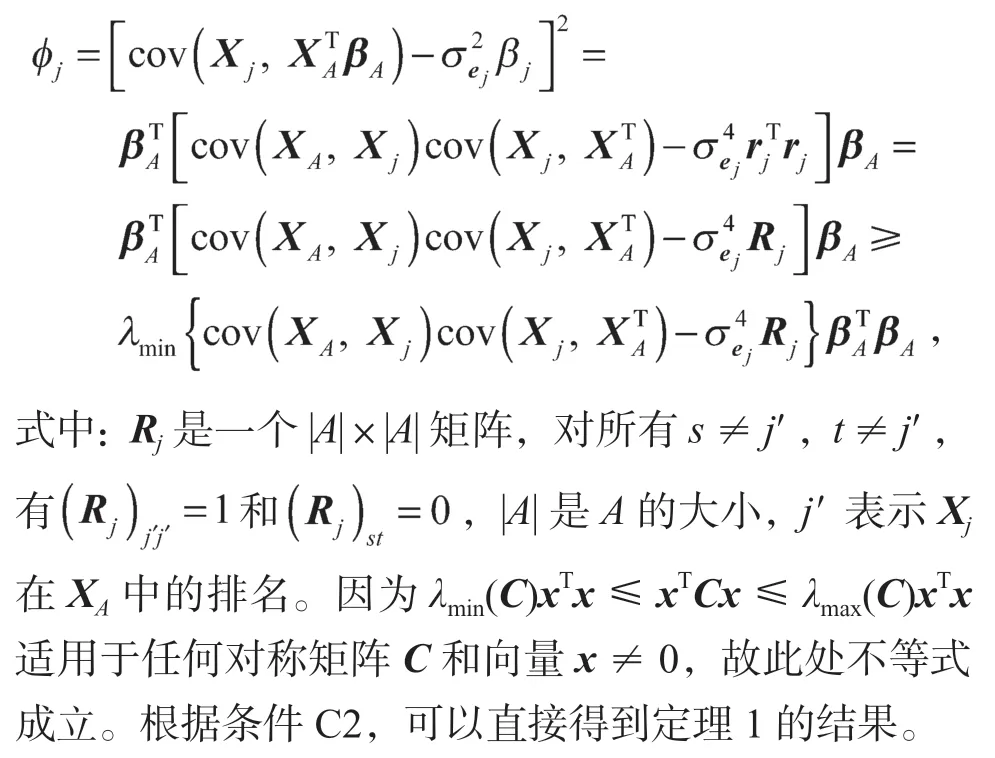
定理2 的证明为了提高可读性，将证明分为如下两个主要步骤。

步骤1首先

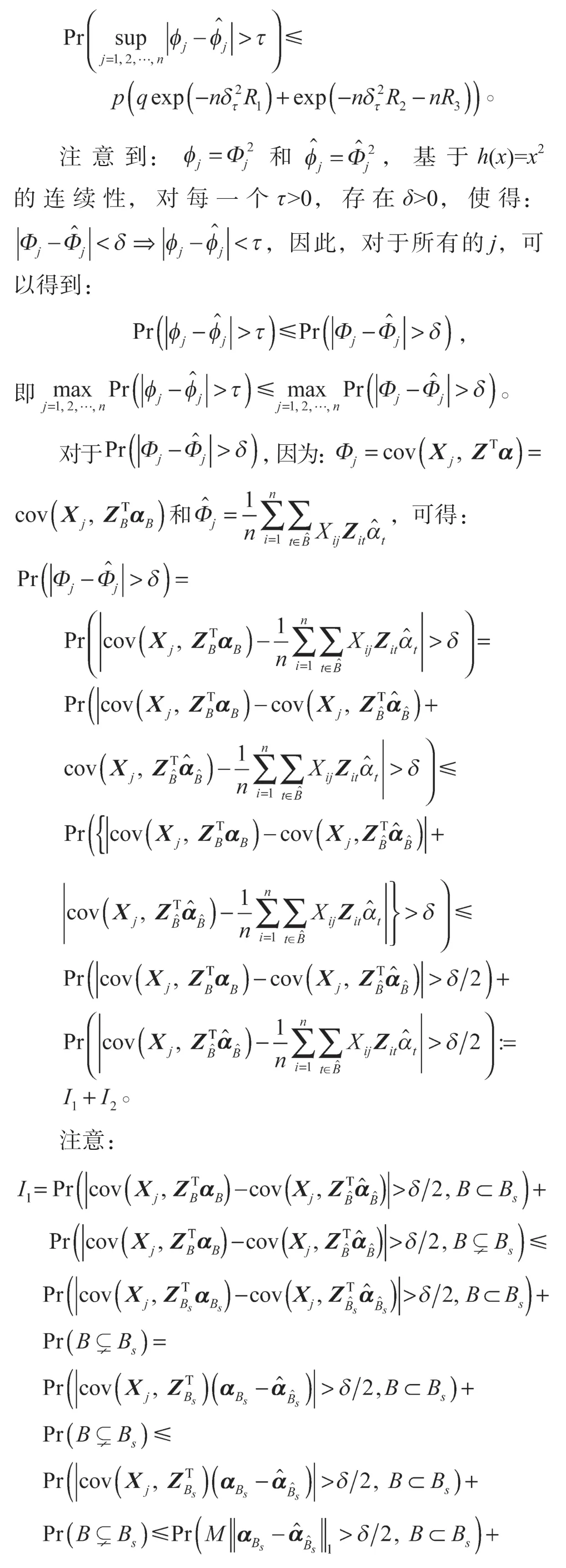
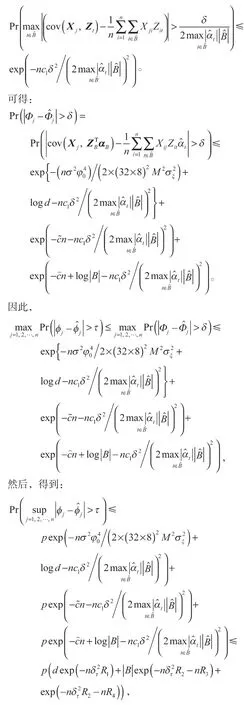
其中，δt=δ是强调δ取决于τ，

5 结语

针对超高维内生协变量的变量选择问题，结合内生协变量和工具变量的相关结构，提出了一种新的用于超高维线部分线性工具变量回归模型的两阶段特征筛选方法，其中内生协变量和工具变量的维数可以随样本量呈指数级增长。理论结果表明，该特征筛选方法在排序上具有一致性。

本文只考虑了工具变量的各分量之间相关性较弱的情况。当工具变量的各分量之间存在高度相关性时，可以使用Hu Q.Q.等[12]给出的条件特征筛选程序来处理。然而，在对内生性协变量的工具变量调整过程中，如何事先确定一个工具变量的备选集合，然后从中筛选重要的工具变量，是当前内生性数据统计建模中常遇到的难题之一。另外，值得进一步研究的问题是如何在不事先假定模型结构的前提下，完全基于内生变量与工具变量的相关结构来构造特征筛选方法。这些问题都有待进一步深入研究。