基于DDA 方法的排碴井筒堵塞概率分析

阳生权，周云锋，吕中玉，彭程武

（1.湖南科技大学 土木工程学院，湖南 湘潭 411201；2.广西路桥工程集团有限公司，广西 南宁 530200）

0 引言

石根华[1]提出的非连续变形分析（discontinuous deformation analysis，DDA）方法对块体间接触问题的科学合理处理，是该方法得以科学实施的关键[2-7]。不论是岩石材料抑或非岩石材料、静力问题抑或动力问题[8-15]，因DDA 方法在模拟岩块移动、转动以及块体间的张开与闭合等方面颇具优势，并且在计算过程中涉及质量与时间因素，这些年在边坡与场坝稳定性分析、爆破及其效应模拟、块体与颗粒重力作用与运动轨迹以及DDA 方法的验证、完善与发展等方面得到了广泛应用[13-19]。

深圳坪盐通道工程马峦山隧道的通风竖井设计开挖断面直径为16.8 m，井筒开挖深度为170 m，属于超大直径竖井，设计采用“钻机反井正向扩大法”施工（其工艺流程见图1），先自上而下导孔（Φ=250 mm）贯通竖井，然后反钻形成1.4 m 直径井筒，再以钻爆法扩孔（Φ=3.0 m），最后以正向钻爆法全断面爆破开挖（Φ=16.2～16.8 m）。由于前期隧道施工工期过长，大大压缩了通风竖井的建设工期；同时，考虑到基于钻爆法扩孔成井工序因开挖断面过小、施工难度与强度过大、安全与工期不可控等，经多方与专家论证，建议跨过钻爆法扩孔工序，反井扩孔后即全断面爆破开挖至设计直径，并利用反钻扩孔井筒自上而下排碴。但是，由于排碴井筒直径过小，排碴过程存在井筒堵塞的危险，且井筒长度较长，井筒堵塞初期难于被及时发现，堵塞后疏通难度非常大，势必影响施工工期。因此，预测各种工况条件下排碴井筒的堵塞概率，控制抛石即爆破岩石块的大小，进而指导竖井全断面爆破施工，保证竖井施工的顺利进行，显得十分必要。

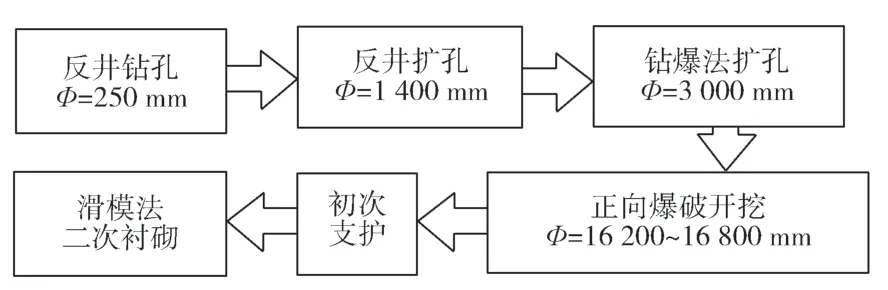
图1 竖井施工工艺流程Fig.1 Flowchart of the shaft construction

岩块在井筒中的下落过程涉及块体碰撞与摩擦等力学行为，属于非连续变形动力学过程。因此，本文利用DDA 方法的自身优势，建立井筒抛碴模型，主要考虑排碴井筒内壁平整度与抛入排碴井筒的岩块块度，分析不同岩块大小、井筒内壁平整度和排碴井筒堵塞概率之间的关系，最后得出相应的爆破岩块与抛石控制尺寸，避免小直径排碴井筒堵塞现象，安全顺利地指导通风竖井施工。

1 排碴井筒堵塞影响因素与数值建模分析

1.1 排碴井筒堵塞影响因素分析

排碴井筒是否会发生堵塞，主要与排碴井筒内壁平整度和抛入排碴井筒的岩块块度及井筒长度有关。

1）排碴井筒内壁平整度。井筒内壁平整度会在很大程度上影响排碴，平整度愈差，抛入井筒的岩块被卡住的概率越大，排碴井筒发生堵塞的概率愈大。井筒内壁平整度与井筒成井质量密切相关，工程地质条件复杂地段，成井质量一般较差，而围岩完整性较好的地段钻孔成孔质量较高，井筒内壁相对平滑。依托工程的排碴井筒处于地表浅层，围岩级别为Ⅳ级、Ⅴ级，岩性一般，成井质量引起的井筒内壁平整度问题会在一定程度上影响抛石的运动轨迹，进而引起井筒堵塞现象。

2）抛入排碴井筒的岩块块度。块度越大的岩块，顺利通过排碴井筒的可能性越低，排碴井筒发生堵塞的概率越高。

3）井筒长度。排碴井筒愈长，抛入井筒岩块的运动轨迹愈复杂，大量岩块同时抛入时，造成井筒堵塞的概率愈大。

此外，抛入井筒岩块的形状、岩块与井筒内壁之间的摩擦因子等因素也会影响井筒堵塞概率，但这些因素较上述因素而言，影响程度相对较低。

基于上述分析，确定控制同时抛入大尺寸岩块数量时，对一定井筒长度的井筒堵塞概率分析应重点考虑井筒内壁平整度和抛入岩块块度，以及岩块形状的影响。

1.2 堵塞概率模型建模分析

正如前文分析所述，岩块在井筒中的下落过程是一种非连续变形动力学过程，因此本文基于非连续变形分析方法与原理，构建井筒排碴堵塞模型。

第三，大数据技术为“零工化”的需求和供给提供了快速处理海量的、非结构化数据、时效性强数据的能力。在大数据技术出现以前，“零工化”的需求和供给都是存在的，但是苦于无法相互匹配，使得潜在的交易无法实现，大数据技术的出现能够很好地处理“及时数据”，实现供给和需求的匹配。不仅如此，大数据强大的计算能力，使得碎片化、个性化、分散化的服务需求和供给能够实现最优的匹配。

基于DDA 方法开发分析软件，以球体作为基本块体单元，基于捆绑算法将球颗粒捆绑成相应形状块体，模拟块体运动过程中的碰撞、摩擦等。图2 所示为部分岩块的模拟形态。固定边界面用三角形构建，通过拼接来模拟各种复杂曲面。

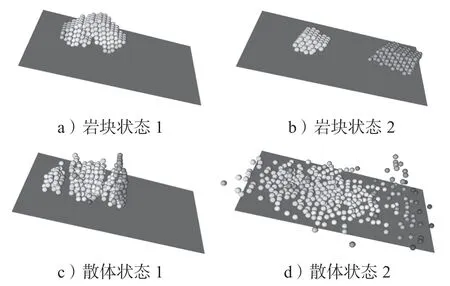
图2 岩块的模拟状态示意图Fig.2 Rock block simulation schematic diagram

假设井筒堵塞过程为一个岩块卡在井筒中间，导致随后抛入井筒中的岩块被卡住，进而形成堵塞长度逐渐变长的堵塞段。通过建立多种岩块模型和不同内壁平整度井筒模型，模拟岩块被抛入井筒后的下落过程，跟踪岩块下落状态，统计判断井筒堵塞风险。为了体现相同岩块以不同角度抛入井筒，岩块随机旋转一个角度后再抛入井筒，并重复20 次。图3 为模拟某一尺寸岩块在井筒中下落过程的未发生堵塞（图3a）与发生堵塞案例（图3b）。

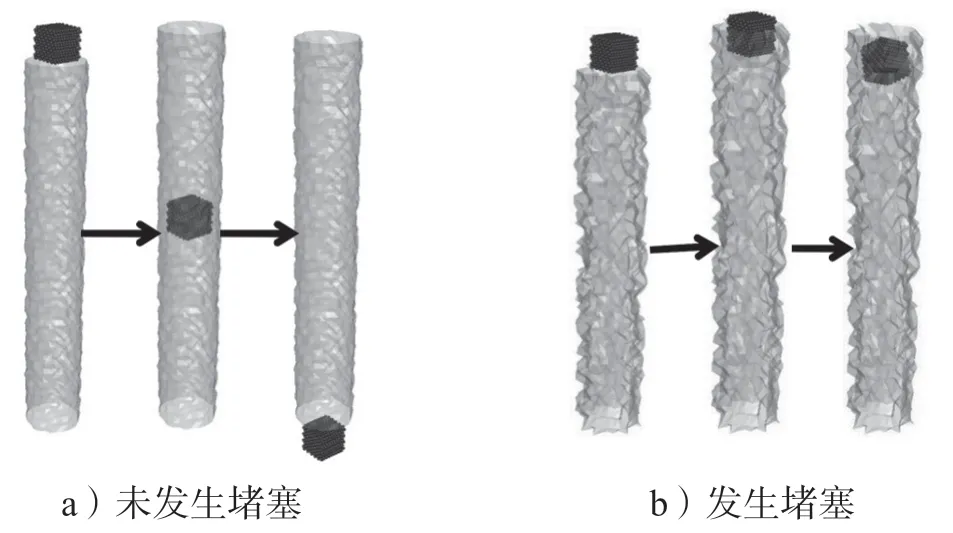
图3 排碴井筒落石过程模拟图Fig.3 Mucking shaft rockfall process simulation diagram

2 概率分析模型的建立

2.1 依托工程概况

依托工程中的通风竖井位于线路西侧，深约为194.0 m，开挖直径为16.8 m。根据勘测资料，隧道通风竖井所处地层为强风～微风化花岗岩，其中强风化花岗岩层厚约25.0 m，中风化、微风化层厚约170.0 m，因此，通风竖井爆破开挖高度约为170.0 m。

2.2 井筒模型高度与直径

据上述分析，井筒模型在高度方向上的形态变化不大，故选取一定高度井筒建模即可，考虑到排碴井筒的直径仅为1.4 m，因此选取井筒模型高度为10.0 m，井筒直径取1.4 m。相对10 m 高度井筒，更低位置井筒同一岩块被卡住的可能性更低，因为在重力作用下岩块的下落速度会越来越快，若岩块能顺利通过10 m高的井筒，则可认为岩块能穿过170 m高的井筒。

2.3 排碴井筒内壁平整度随机模拟

井筒内壁的不平整性表现为井筒内部曲面的凹凸程度，且不同位置处的凹凸程度不完全确定，存在一定的随机性，但一定程度上服从概率分布，且该随机分布与成井施工过程与工程地质条件有关。

图4 为排碴井筒模型某一高度的截面图，设计钻孔成井，井筒内壁半径为0.7 m，因为围岩地质条件与钻孔成井施工等方面的影响，实际井筒内壁会出现一定程度的超挖与欠挖现象，本文采用Monte Carlo方法获取随机数，并用随机数表征井筒内壁各点到井筒中心线的距离，使井筒内壁各点到井筒中心线的距离以0.7 m 作为中心上下随机浮动，浮动的最大值为平整度体现值，将这些随机分布的点每3 个点连成一个三角面，最终拼接成凹凸不平的复杂曲面。

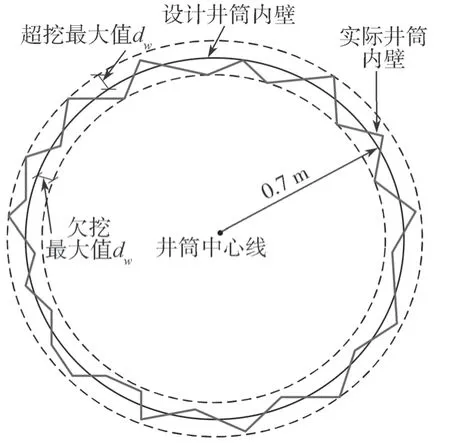
图4 井筒内壁随机模拟示意图Fig.4 Random simulation diagram of the wellbore wall

根据现场钻孔成井质量的实际情况与统计规律，构建4 种超欠挖水平井筒模型（见图5），超欠挖水平从0.01 m 逐渐增大至0.15 m。

图5 不同平整度内壁的井筒模型Fig.5 Wellbore model of inner wall with different flatness

2.4 不同块度岩块模拟

竖井爆破形成的岩石块体实际的岩块块度与形状千差万别（见图6），统计发现，扁平或细长的岩块几乎不会出现，带有长尖棱角的岩块也很少。根据施工现场岩块的实际情况，可对不同块度的岩块模拟进行合理简化。图7 为部分模拟岩块的模型示意图，具体是将岩块模拟成不同尺寸的长方体，而岩块断面为正方形，正方形边长分别为0.2,0.4,0.6,0.8,1.0 m，根据现场爆破参数（炮孔深度为3.0 m）岩块最长边取3.0 m，通过改变高宽比来构建多种尺寸的岩块，考虑到细长岩块出现的可能性极低，故将构建的岩块高宽比最大值限定为4.0，共构建了32 种岩块，岩块尺寸为（0.2 m×0.2 m×0.2 m）～（0.4 m×0.4 m×0.8 m）～（1.0 m×1.0 m×3.0 m），考虑到最大尺寸小于井筒直径（1.4 m）的岩块造成井筒堵塞的概率极低，为简化统计与描述，仅选取较大尺寸的20 种岩块模型进行概率统计与分析。岩块块度定义为长方体岩块模型两个对角顶点之间的距离。

图6 排碴现场岩块Fig.6 Rock blocks at the site

图7 部分岩块模型Fig.7 Rock block model samples

3 井筒堵塞概率统计结果与分析

针对构建的32 种岩块模型，选取较大尺寸的20种岩块模型、4 种不同超欠挖水平的井筒模型，进行各个岩块模型20 次随机角度抛入井筒模拟试验，共计进行20×4×20=1 600 次数值模拟试验。模拟计算采用黄刚海设计的“三维颗粒非连续变形分析软件（PDDA3D）”，最终统计出相应的堵塞概率，所得结果如表1 所示。图8 和图9 分别为堵塞概率与块度间的关系图和堵塞概率与超欠挖水平关系图，图9中岩块尺寸单位为m。

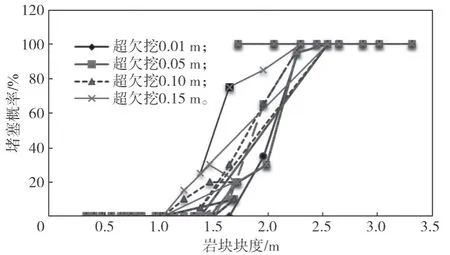
图8 堵塞概率与块度间的关系曲线Fig.8 Relationship curves between blockage probability and block sizes

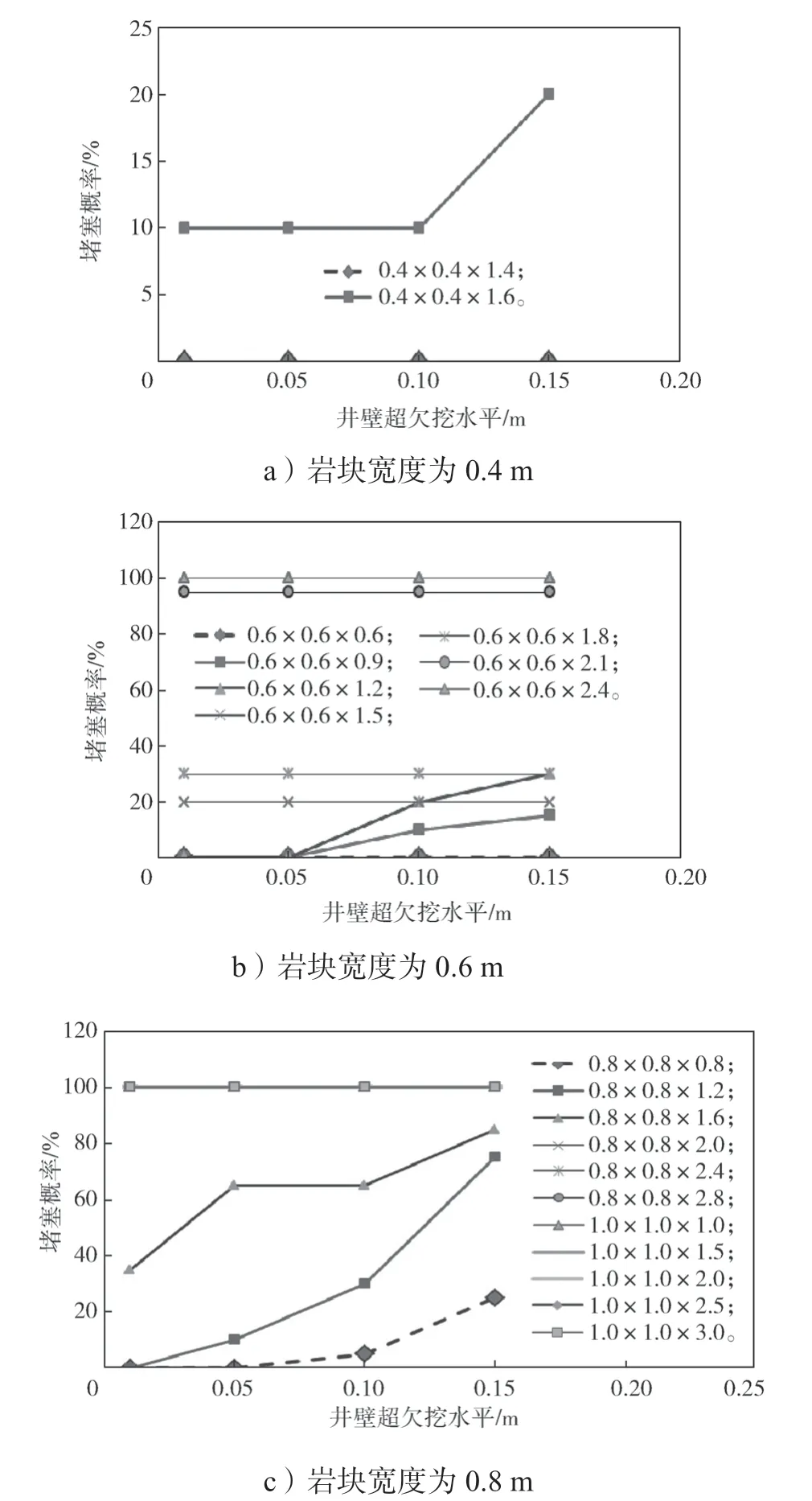
图9 堵塞概率与超欠挖水平间的关系曲线Fig.9 Relationship curves between blockage probability and the under-excavation horizontal space

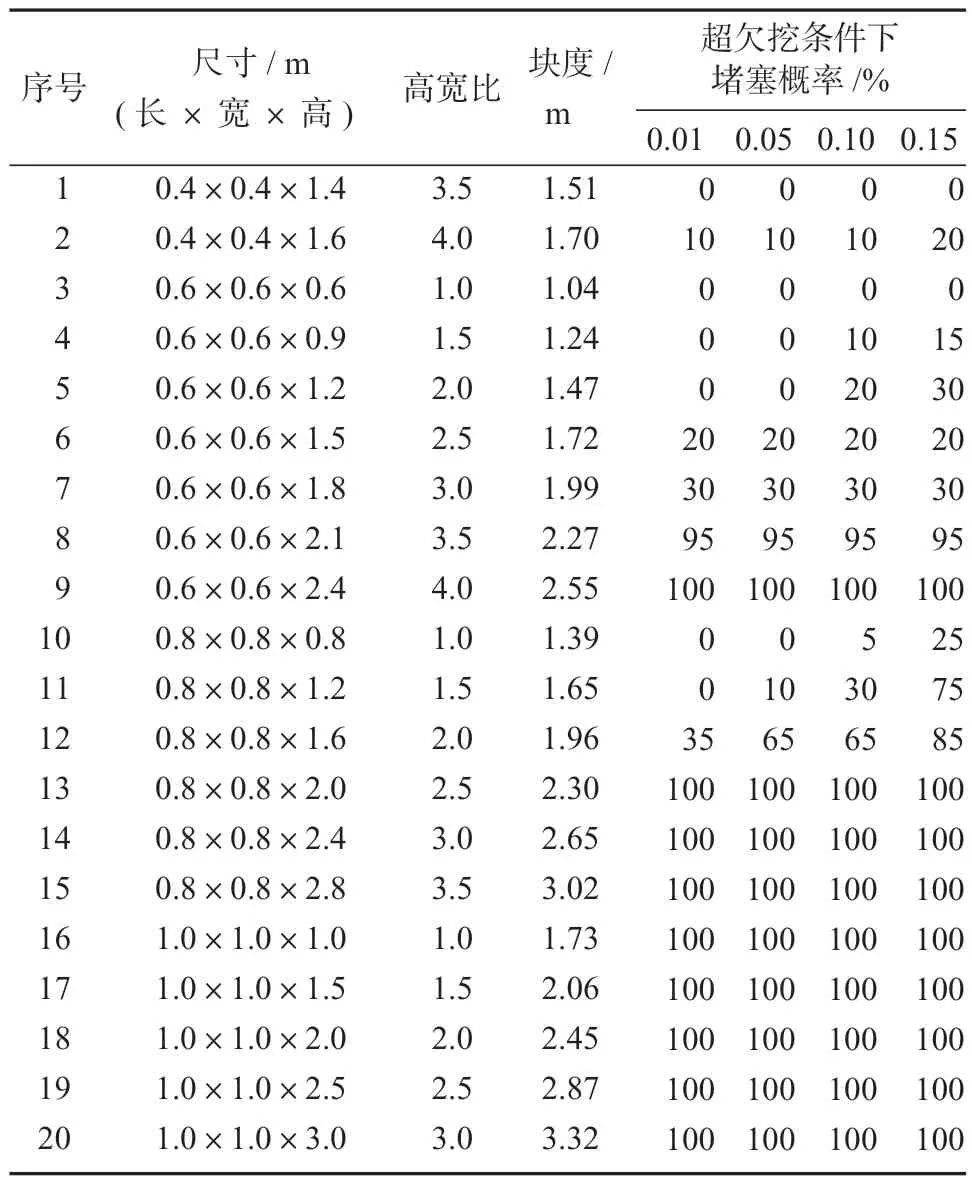
表1 不同平整度井筒模型落石堵塞概率分析模拟结果Table 1 Simulation results of rockfall blockage probability analysis for wellbore models with different flatness

分析表1 与图8 发现，块度低于1.00 m 的岩块，不管形状如何，在所有井筒模型中均不会发生堵塞。块度大于2.25 m 的岩块，几乎都会发生堵塞现象。说明块度小于1.00 m 的岩块均可抛入排碴井筒；而块度大于2.25 m 的岩块一律不得抛入排碴井筒，需要进行二次破碎；块度介于1.00～2.25 m 的岩块，根据岩块宽度酌情决定是否抛入井筒，宽度较小时可抛入，或不得连续抛入。所有宽度为1.00 m 的岩块，在所有井筒模型中均会发生堵塞现象。由此可建议，宽度达1.0 m 的岩块，均不可抛入井筒。

分析表1 和图9 发现，总体上存在井筒超欠挖越严重堵塞概率越大的变化趋势，并且随着岩块宽度增大，增大趋势越明显。在同类工程中，若是采用钻爆法施工排碴井筒，应严格控制排碴井筒超欠挖水平，建议将0.15 m 列为控制值。

鉴于现场极少出现细长或扁平岩块，单独考虑表1 中高宽比不大于2.0 的岩块，可以得知：

1）宽度不超过0.4 m 的岩块均可抛入井筒；

2）当超欠挖不超过0.05 m 时，宽度不超过0.6 m 的岩块均可抛入井筒。

当排碴井筒超欠挖水平为0.10～0.15 m 时，可以得出：

1）宽度不超过0.4 m、长度不超过1.4 m 的岩块均可抛入井筒；

2）宽度不超过0.6 m 且接近正方体的岩块，均可抛入井筒。

4 结论与建议

直径1.4 m井筒可能在排碴过程中发生堵塞现象，将严重影响建设工期。在分析井筒排碴过程中堵塞影响因素的基础上，基于DDA 方法，通过数值建模，并通过对不同块度岩块与4 种超欠挖井筒模型的模拟，开展了针对性的小直径井筒落石堵塞概率分析，为排碴井筒顺利排碴提供了理论依据与实践指导，保证了竖井施工工期与安全，具体结论与建议如下：

1）小直径排碴井筒会发生堵塞现象，为避免堵塞现象的发生，应严格控制抛入排碴井筒的岩块尺寸与块度；

2）钻爆法施工的小直径排碴井筒往往会出现超、欠挖现象，井筒超欠挖现象越严重，堵塞概率越大；

3）研究成果可为同类工程的竖井施工、爆破施工与爆破块度控制，以及小直径竖井排碴控制提供借鉴与参考。