基于改进聚类分析的电力数据智能分析与处理算法

张 超，武 泽，许 峰，姚天赐

（国网伊犁伊河供电有限责任公司，新疆伊犁 835000）

随着传感器技术和通信技术的不断发展，使用众多技术的电网也更加趋于智能化。同时产生的电力数据也呈现指数增长，如何高效利用海量电力数据，为电网稳定运行提供支撑成为了亟待解决的问题[1-2]。

在数据存储、通信以及数据整合、挖掘等方面，已有大量相关的电力数据分析处理算法[3]。文献[4]结合人工智能技术综合挖掘分析电力变压器状态数据，以提升设备状态检修的全面性与准确性。文献[5]利用并行反向传播神经网络算法分析海量用户侧数据，实现负荷分类。文献[6]基于粒子滤波和卷积神经网络分析电网运行监控数据，有效提高了状态估计精度和鲁棒性。但现有的电力数据分析处理算法无法满足智能电网对精细化和时效性的需求，为此，该文基于改进聚类分析算法提出了一种能够对电力数据进行智能分析与处理的方案。利用布谷鸟搜索(Cuckoo Search，CS)算法改进高斯混合模型(Gaussian Mixture Model，GMM)，设计实 现了GMM-CS 聚类算法，将其用于电力数据的分析和处理，有效提高了分析处理的准确性与实时性。

1 改进GMM聚类分析算法

GMM 参数的正确估计是实现电力数据智能分析和处理的关键，通常采用极大似然估计确定参数，而期望最大化(Expectation Maximization，EM)是最常用的求解方法。但EM 算法在更新参数估计的过程中存在一些问题，易陷入局部极值[7]；初始值设置对达到似然函数极值有较大的影响[8]；在高维且数据量大的数据集中会生成非法协方差矩阵，无法获取精准的模型参数[9]。为此，采用CS 算法寻找最优的GMM 参数值。

1.1 高斯混合模型

假设X={x1,x2,…,xn} 为随机观测数据且由某个GMM 生成，其中xj∈Rd,j=1,…,n是d维随机变量，数据之间相互独立，含有M个单高斯模型分量。

观测数据样本GMM 概率密度表示如下：

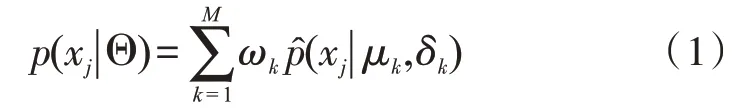
式中，ωk为每个单高斯模型的权重，且相加为1；Θ={ω1,μ1,δ1;…;ωM,μM,δM} 为GMM 的参数集合；μk∈Rd、δk(d×d),k=1,2,…,M分别为第k个单高斯模型的均值向量和协方差矩阵；为单高斯模型的概率密度，公式为：

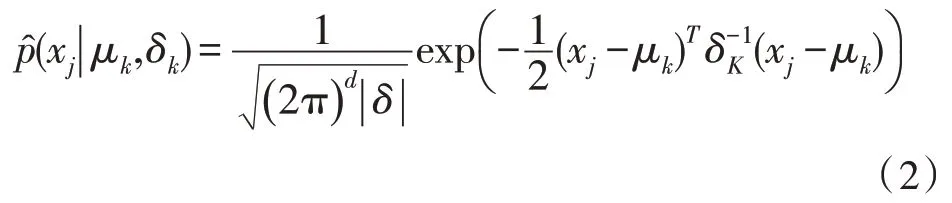
对于观测数据，假定各个样本之间具备统计的独立性，则数学表示如下：

式（3）为Θ 关于X的似然函数，则定义其对数似然函数为：

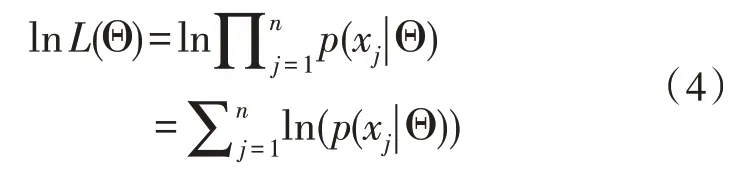
通过求解式（4），便可得到对数似然函数的最大值，即：

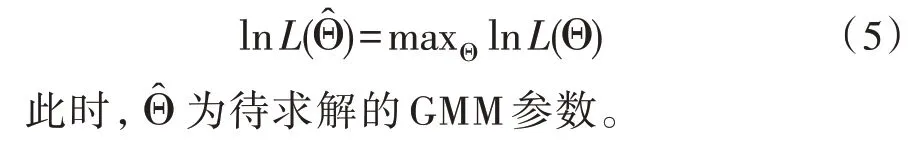
1.2 布谷鸟搜索算法

CS 算法主要来源于布谷鸟巢的寄生机制和Levy飞行的基本原理，为了便于分析，假设在CS 算法中每个布谷鸟的筑巢和产卵过程中能够检测到外来卵的概率是pa。同时，对于待解决的问题，为了简化计算过程，用巢中的卵来代表相应问题的解决方案，每个卵代表一种新的策略，旨在用更好的策略取代更差的策略，且巢的空间位置就是卵的位置。

布谷鸟巢位置更新如下：

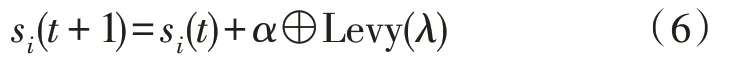
式中，si(t)为第i个布谷鸟在第t次迭代中的嵌套位置；⊕表示点乘；α为步长，α＞0。实质上，式（6）表示一个随机游走过程，并遵循马尔可夫链，其未来空间位置主要受当前位置和转移概率的影响。Levy(λ)表示随机搜索当前路径，数学表示如下：

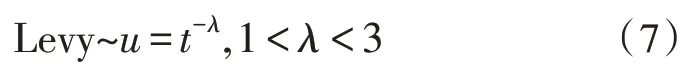
CS 算法的基本流程如图1 所示。

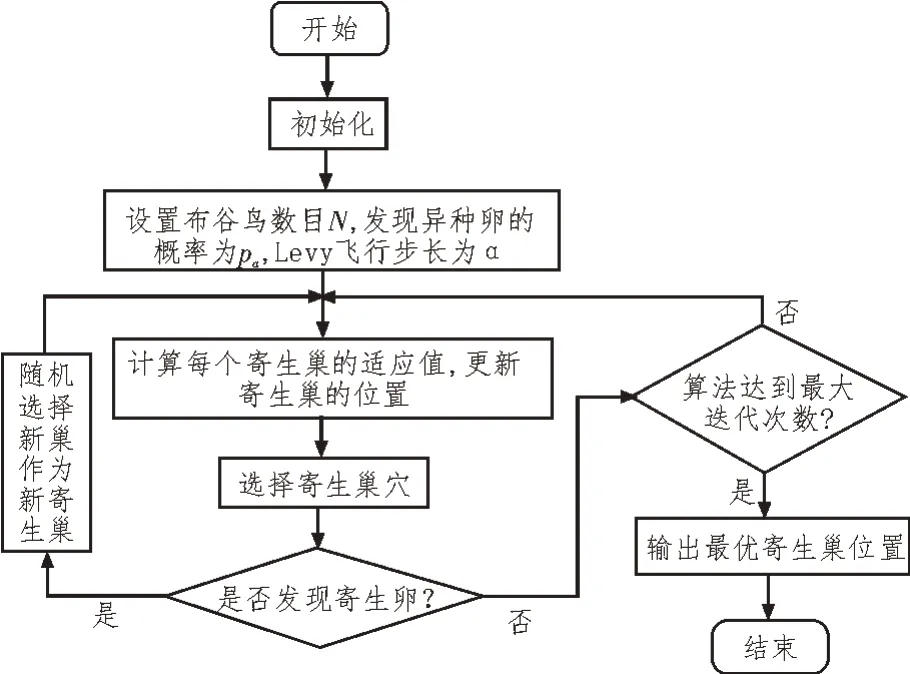
图1 CS算法的处理流程

从CS 算法流程可以看出，该算法原理清晰、流程简单，但Levy 飞行的实现相对复杂。在算法中，寄生巢的位置越来越集中，则Levy 飞行步长缩小，因此算法在较小的局部范围内进行搜索[10-12]。由于Levy飞行操作和宿主放弃寄生巢，CS 算法具有较强的跳出局部最优解的能力[13]。

1.3 GMM-CS聚类分析

利用CS 算法求解GMM 参数的最优解，从而构成GMM-CS 聚类方法，对电力数据进行智能分析和处理。其中GMM-CS 聚类分析的流程如下：

1）初始化种群规模及相应参数。根据数据集维数d、GMM 分量个数M设置GMM-CS 算法个体长度D和种群规模Np。其中Np和D的计算如下：

CS算法的参数初始化为：pa=0.25，s0=[0 0.25]，u0=[1 0.75]。

2）将训练数据集进行Np次GMM 聚类，计算出每一次聚类的均值向量和协方差矩阵，以得到初始种群的每个个体。

4）根据给定的CS 算法的寄生机制和Levy 飞行原理，对所有个体进行优化选择，产生新的种群。同时更新每个个体的适应值，并计算最优适应值。

5）判断迭代次数是否达到最大，若达到最大，则转到6）；否则转到4）。

6）将最优个体和对应的最优适应度函数值输出，即可得到最优的GMM 参数。

2 电力数据智能分析与处理算法

随着信息技术在电力系统的广泛应用，要保证其安全运行，需要对电力数据进行有效分析[14-15]。通过构建电力数据智能分析处理系统，为改进聚类分析的应用提供条件，从而实现准确、高效的数据异常分析并采取预防措施。

2.1 智能分析处理系统架构

通过构建电力数据智能分析处理系统，可以利用电网数据进行聚类分析、时序预测等，并根据分析结果划分为多维数据，为电网数据的应用提供参考。其中，电力数据智能分析处理系统的架构如图2所示。

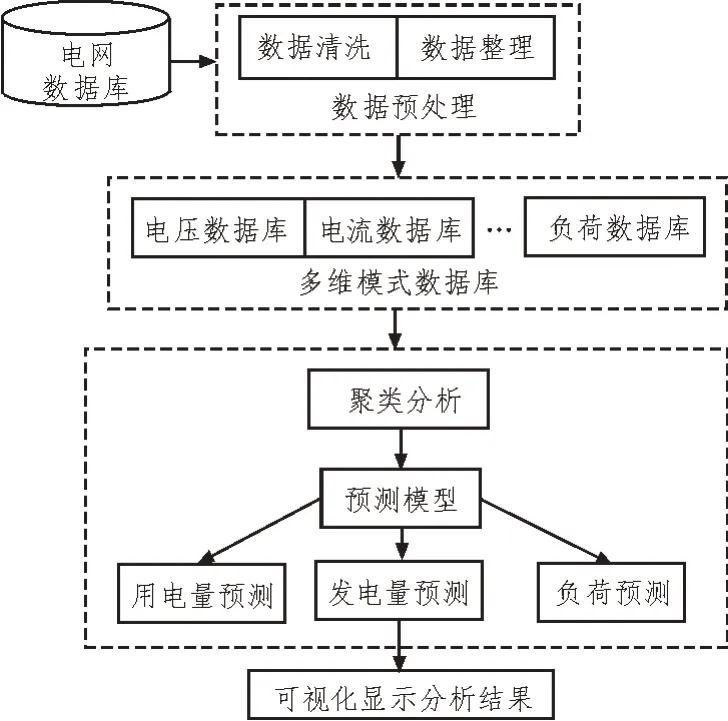
图2 电力数据智能分析处理系统的架构

2.2 基于GMM-CS的电力数据智能分析处理算法

对于给定的电力数据样本，其智能分析的目标是识别异常数据并采取处理措施[16]。在电力数据异常分析任务中，目的是找到异常数据Θ*，其对应的模型Θi使得待分析电力数据组具有最大后验概率P(Θi|X)。基于GMM-CS 的电力数据分析和处理算法的架构如图3 所示。

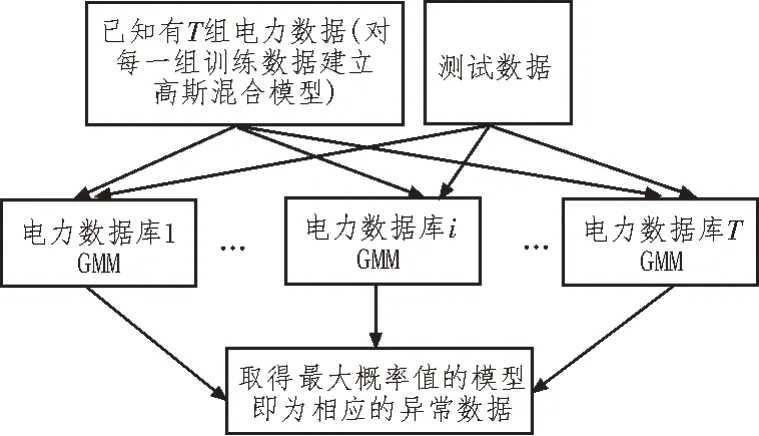
图3 基于GMM-CS的电力数据分析和处理算法的架构基于贝叶斯理论，最大后验概率可表示为：

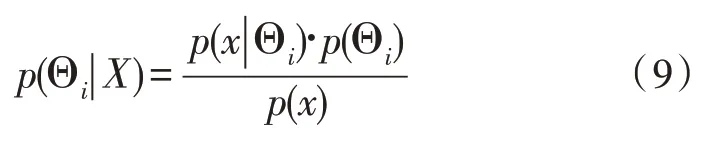
对于Θi的先验概率p(Θi)，如果没有先验知识，则1 ≤i≤T。在电力数据的智能分析和处理中，p(Θi) 为训练数据中第i组异常数据与总数据量的比值，即训练集中第i组数据存在的异常数据越多，其先验概率越大。对于一个确定的特征量x，p(x) 是一个确定的常数，所有异常数据的p(x)均一致。因此，求取后验概率可以通过求取p(x|Θi)·p(Θi)得到。如此，分析电力数据中异常数据便可表示为：

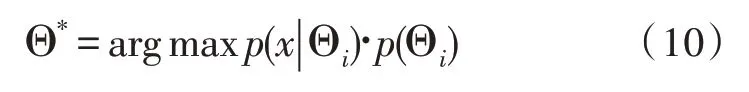
3 实验结果与分析

3.1 GMM-CS模型分量参数分析

为了确定GMM-CS 模型分量的最优个数，采用模型中封装的Akaike Information Criterion(AIC)和Bayesian Information Criterion(BIC)两个指标评估调整模型，结果如图4 所示。其中AIC 和BIC 的数值越小，说明模型的性能越优。

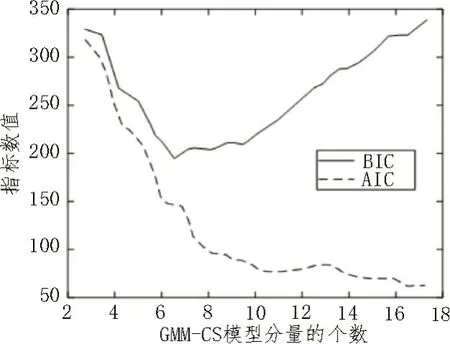
图4 AIC、BIC与GMM-CS模型分量个数的关系

从图4 中可以看出，当GMM-CS 模型分量个数大约为6 时，BIC 数值达到最小。而AIC 数值随着GMM-CS 模型分量个数的增加持续减小。但当分量个数达到10 之后，AIC 数值变化较小。因此综合考虑，将GMM-CS 模型的分量个数设为10。此时AIC和BIC 数值均接近最小，因此模型的聚类效果最为理想。

3.2 所提算法收敛性对比分析

为了能够更加直观地看出所提算法的收敛性能，将其与文献[5]、文献[6]、文献[10]进行对比分析，结果如图5 所示。

图5 不同算法的收敛性对比结果

从图5 中可以看出，相比于其他算法，所提算法的在迭代约75 次即实现收敛，收敛速度快。由于所提算法采用CS 算法寻得GMM 模型的最优值，避免局部最优，加快了寻优速度。文献[5]的反向传播神经网络、文献[6]结合粒子滤波和卷积神经网络，分析算法复杂，均在约150 次实现收敛。而文献[10]采用数据挖掘进行数据分析，所使用的是传统算法，未进行优化和改进，收敛性并不理想。

3.3 电力数据分析处理性能对比

电力数据智能分析的重要应用之一是系统故障检测，如网络入侵、各种短路故障等[17-18]。目前系统对可能出现的异常已有明确的界定，因此可采用检测率和误检率进行性能评价。其中检测率为数据集中被算法检测出的异常数据个数与所有异常数据个数的比值；误检率为数据集中被误检为异常的正常数据个数与所有正常数据个数的比值。四种算法的对比结果，如表1 所示。

表1 不同算法数据分析处理性能对比结果

从表1 中可以看出，所提算法的检测率、误检率分别是95.35%和7.81%，均优于其他对比算法。所提算法采用改进聚类分析模型实现全局搜索，保证了数据分析的准确性。而文献[10]采用数据挖掘技术，由于算法步骤较为简单，因此耗时仅为14.37 s，短于所提算法的16.54 s，但其整体性能不佳，误检率超过了10%。文献[5]采用反向传播神经网络以及文献[6]结合粒子滤波和卷积神经网络实现电力数据分析，检测率和误检率较为理想，但算法较为复杂，耗时较长，均超过20 s。综合检测结果与耗时，所提算法的整体性能最佳，能高效且准确地分析电力数据并采取相应的措施。

4 结束语

电力数据的精准分析对电网的稳定运行至关重要，为此该文设计了一种电力数据智能分析与处理算法，以提高数据分析的准确性和时效性。通过求解GMM 参数的最优解，避免了算法陷入局部最优。同时将GMM-CS 改进聚类算法用于处理系统内的多维模式数据库，从而获得异常数据。此外实验结果表明，当GMM 参数个数设为10 时，所提算法性能最佳，且其迭代次数约为75，检测率、误检率分别是95.35%和7.81%，分析时间为16.54 s，整体性能优于其他对比算法。对于庞大的电力系统而言，时效性是重要的指标，因此在接下来的研究中，将考虑将算法与分布式相结合，进一步提高运行速度，增强算法的实用性。