基于LeapMotion 的手势识别算法改进与研究

韩彦鹏，秦飞舟

（宁夏大学物理与电子电气工程学院，宁夏银川 750021）

随着科学技术的不断进步,人机交互向着越来越便捷的方向发展，各种体感设备都对人机交互方式产生了巨大影响，人们的生活方式也因人机交互而发生改变[1]。在人机交互技术领域中，手势交互正在成为行业的热点之一。在手势交互技术中，手势识别算法是最为关键的内容。

1 数据采集

1.1 手势采集设备

目前，手势采集的方式主要有数据传感手套和视觉信息采集两种。数据传感手套的采集方式为通过在手指、指尖和手背等部位佩戴传感器，采集手部动作数据发送到电脑端；视觉信息的采集方式为通过摄像头采集规定空间领域内的信息图像，发送到电脑端。

常用的视觉信息采集设备有Kinect[2]和Leap-Motion[3]两种。LeapMotion 具有的红外滤光膜能消除特定场景下光线明暗变化带来的准确性偏差问题，对环境依赖性更小，手部识别的准确性更高，它的工作距离的范围为25～600 mm，扫描频率为每秒200 帧，150°的大视野范围使其捕捉系统更具有准确性和应用性[4]。文中采用LeapMotion 作为采集工具，图1 为LeapMotion 拆分结构，图2为LeapMotion工作范围。

图1 LeapMotion拆分结构

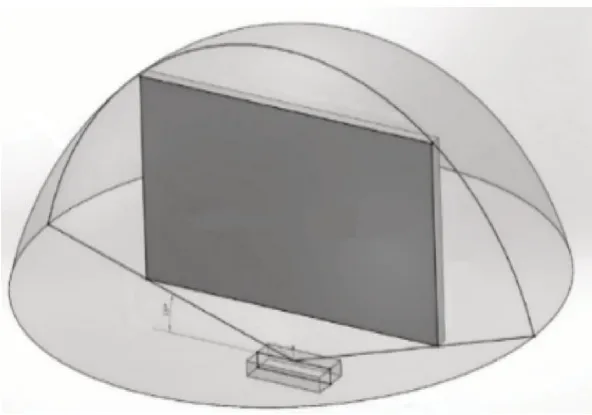
图2 LeapMotion工作范围

1.2 手部节点模型及提取特征

LeapMotion 通过对手部节点位置和运动特征追踪、定位，完成手部数据记录，手部节点模型[5]如图3所示。手部运动特征[6]由指尖方向向量和掌心法向量组成，如图4 所示。采集到的数据以文本格式存储到指定的文件夹内。

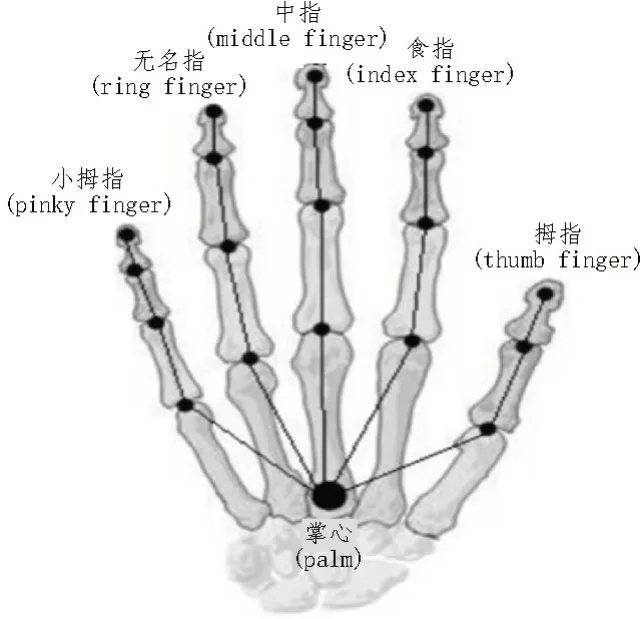
图3 手部节点模型

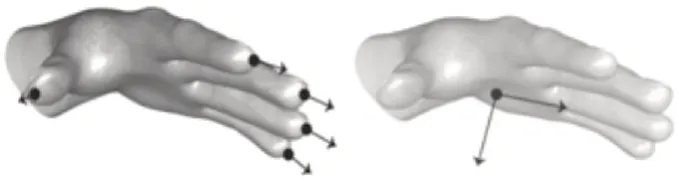
图4 指尖方向向量和掌心法向量

1.3 手势采集系统的搭建

手势数据采集环境由PC 机和LeapMotion 设备组 成。在PC 机上安装LeapMotion SDK（Software Development Kit）、Python2.7 编译器和PyCharm 平台组成开发环境。PC 机负责存储采集到的手部数据，LeapMotion 作为手部数据采集的硬件。

1.4 手势数据集

构建的手势数据集设计了以下五种手势样本：剪刀、石头、布、GOOD、OK，如图5 所示。通过Python程序完成对五种手势数据的多次收集并建立数据集，每种手势设置了120 组训练数据。

图5 五种手势样本

2 改进KNN算法

2.1 K-近邻算法

K-近邻算法（K-Nearest Neighbor,KNN）是一种基本的分类与回归算法，1968 年由Cover 和Hart 提出，通过测量不同特征值之间的距离来进行分类，具体原理：给定一个训练数据集，对新输入的实例，在训练数据集中找到与该实例最邻近的K个实例，如果这K个实例的多数属于某个类，就把该实例归于这个类[7-8]。如图6 所示，有A 和B 两类不同的样本集，待分类样本点为C，在与C 相邻最近的六个点中，A 类有四个，B 类有两个，由此判定点C 属于A 类。

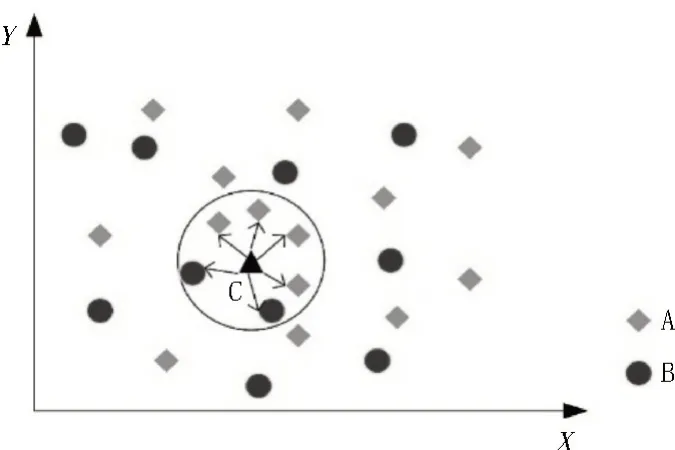
图6 K-近邻算法分类原理图

2.2 KNN算法的优缺点

KNN[9]算法以其稳定性好、准确率高等特点受到广泛应用，但其对训练数据依赖程度较大。若在训练数据集中，有一两个数据是错误的，恰好又在需要分类数值附近，则会导致预测数据不准确，对训练数据的容错率较低。KNN 算法对于“维数灾难”问题也未能很好地解决，由于每个待分类的样本都要计算它到全部点的距离，根据距离排序求得K个邻近点，在面对高维度数据（维度不小于2 且拥有多个属性的数据）时，分类的准确性会受到影响。

2.3 SVM算法改进KNN算法的理论基础

支持向量机（Support Vector Machine，SVM）算法是采用结构风险最小化准则设计的，考虑了经验风险和置信范围[10]。对于非线性问题，通过线性变换转到高维度的特征空间，在高维特征空间[11]中构造线性判别函数来实现训练样本分类，其算法复杂度与特征空间的维数无关，避免了“维数灾难”问题。

SVM 算法主要针对有限样本情况，其目标是得到现有信息下的最优解，而不仅仅是样本数趋于无穷大时的最优解，SVM 算法通过学习，选择出只占训练样本集少部分的支持向量，通过SVM 算法处理的数据，可以得到全局最优解。因此SVM 算法可以弥补KNN算法的缺点，文中将利用SVM 算法对KNN 算法进行改进，帮助KNN 算法完成对错误和差值较大数据的预处理，改进的算法命名为S-KNN算法。

2.4 S-KNN算法原理

通过对手势数据进行归一化处理来判断其是否在探测范围内，若在范围内则输入SVM 算法进行下一步手势数据筛选，若不在探测范围内则舍弃数据。手势数据通过算法处理后再次判断是否为良好的手势数据，良好数据的标准为：

1）若手势数据节点（真实风险值）与算法预测值（经验风险最优值）相差超过10%,则舍弃该节点。

2）若两节点（或两个节点以上）在空间位置重合,则去除重合节点。

满足以上两个条件，则判断为良好的手势数据，输入给下一层级的KNN 算法处理。通过两次判断去除不必要的和错误的三维坐标信息[12]，使数据具有更好的训练性和准确性。利用KNN 算法进行手势识别计算，测定哪些手指是张开的，哪些是蜷缩的，通过其蜷缩的程度[13]计算出最终结果。例如需要判断一个剪刀的手势，就需要判断大拇指、无名指和小拇指是蜷缩的，食指和中指是伸开的。通过输出结果来验证S-KNN 算法的鲁棒性[14]和有效识别率，S-KNN 算法流程如图7 所示。

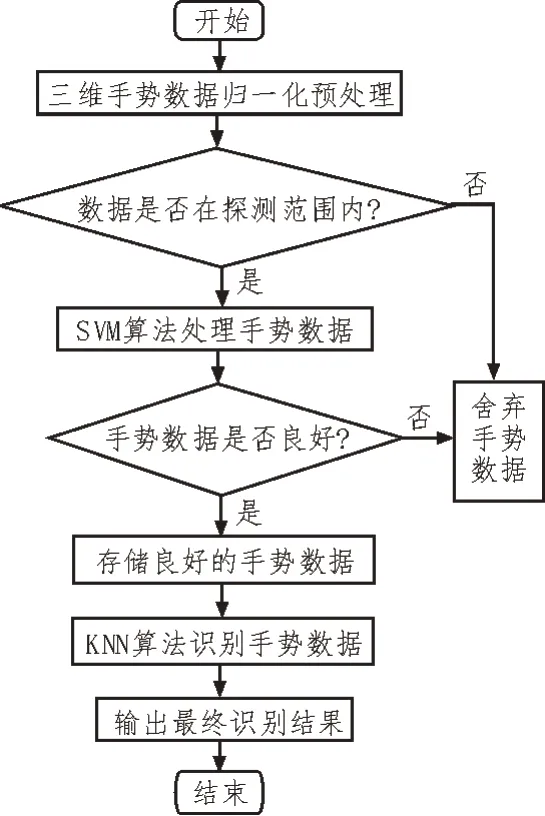
图7 S-KNN算法流程

3 验证结果与分析

3.1 S-KNN 算法与基于欧式距离的KNN 算法的平均识别率对比

如图8 所示，S-KNN 算法与基于欧式距离的KNN 算法[15]的平均识别率随着K值变化的对比图中，线S-KNN-Feature 代表S-KNN 算法的平均识别率，线KNN-EU-Feature 代表基于欧式距离的KNN算法的平均识别率，横轴代表K的取值，纵轴为识别准确率。随着K值的变化二者的识别率有着不同程度的波动，从实验结果可以看出，S-KNN 算法对手势的平均识别率要远远高于基于欧式距离的KNN算法的平均识别率，当K等于10 时，S-KNN 算法对手势的平均识别率达到最高，约为97%，而基于欧式距离的KNN算法对手势的平均识别率只有78.8%左右。

图8 S-KNN算法与基于欧式距离的KNN算法识别率对比图

3.2 S-KNN 算法与基于曼哈顿距离的KNN 算法的平均识别率对比

如图9 所示，S-KNN 算法与基于曼哈顿距离的KNN 算法[16]的平均识别率随着K 值变化的对比图中，线S-KNN-Feature 代表S-KNN 算法的平均识别率，线KNN-MA-Feature 代表基于曼哈顿距离的KNN 算法的平均识别率，从实验结果可以看出，SKNN 算法对手势的平均识别率仍远高于基于曼哈顿距离的KNN 算法的平均识别率，当K等于10～13 时，S-KNN 算法对手势的平均识别率达到97%左右，而基于曼哈顿距离的KNN 算法对手势的平均识别率只有78.2%左右，即使在K=4 时基于曼哈顿距离的KNN 算法对手势平均识别率达到最高，也只有79.8%左右，要远低于S-KNN 算法的平均识别率。综上实验结果可以看出，改进得到的S-KNN 算法对手势的有效识别率[17]有非常明显的提高，平均识别率提高了约15%，验证了该算法的有效性。

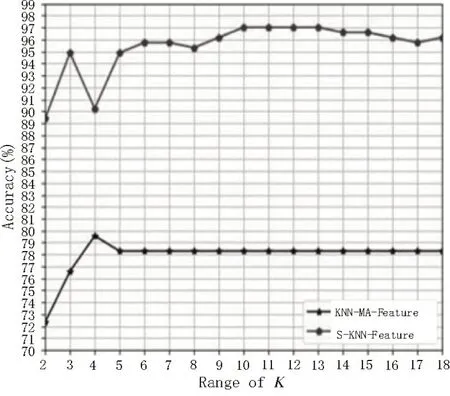
图9 S-KNN算法与基于曼哈顿距离的KNN算法识别率对比图

3.3 S-KNN算法手势识别率混淆矩阵图

如图10 所示为S-KNN 算法的手势识别率混淆矩阵图，横坐标为1、2、3、4、5 代表了“剪刀”、“石头”、“布”、“GOOD”、“OK”五种不同手势的预测手势标签，纵坐标为手势1 至5 的真实手势标签，混淆矩阵y行和x列的值为第y类手势被识别或第x类手势的概率。从实验结果图可以看出，第二行的实际手势“石头”被识别成预测手势的“GOOD”概率为5%，第三行的实际手势“布”被识别成预测手势的“石头”和“OK”概率各为3%，第五行的实际手势“OK”被识别成预测手势的“剪刀”概率为3%，识别错误概率均较低，可以判断S-KNN 算法对五种手势的识别率均为较高水平，在较为理想的情况下平均识别率均达到了95%以上。

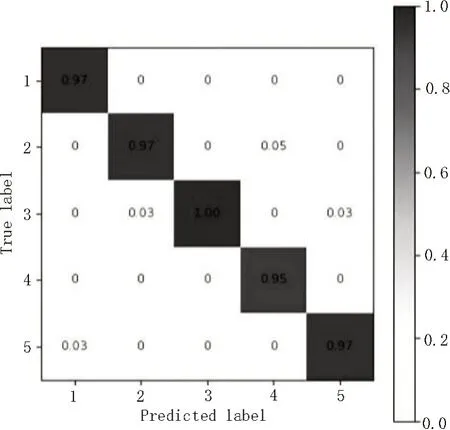
图10 S-KNN算法手挚识别率混淆矩阵

4 结束语

通过以上实验结论可以判断S-KNN 算法相对于传统的KNN 算法手势识别准确率有着较大幅度的提高，对KNN 算法的改进是合理且成功的，利用SVM 算法来改进KNN 算法可以更好地收集到有效训练集，获得更高的手势识别率。