遗传算法在优化输电网络扩建规划中的应用

许 威，林月娥，张 霞

（1.北京城建设计发展集团股份有限公司，北京 100037；2.北京理工大学信息与电子学院，北京 100081）

输电网络扩建规划从建立电力需求增长情景开始，并根据预测结果进行[1]，因此需要加强网络的性能，以使其与电力需求相匹配[2-3]。在不满足电力服务条件的情况下，提出了一个在供电可用性、需求和网络中新设备安装之间具有一致性的方案。为了维持适当的技术和操作条件，将这些新设备整合到网络中，需要规划此类设备的分配[4]。输电网络扩建规划的主要目标是在满足运行和经济约束的前提下，获得最优的扩建方案[5]。

输电网络扩建规划问题的数学表示始于一些假设，在模型构建中考虑了准确性和复杂性[6-7]。输电网络扩建规划问题通常用一个混合整数非线性规划(Mixed Integer NonLinear Programming，MINLP)问 题来表示，该问题为实际系统提供了许多局部最优解。因此，问题的核心在于定义满足所有操作约束的最小成本扩张方案。在长期静态输电扩建规划（规划期限一般在五年以上）中，所有投资均在一年规划期内进行。静态规划的目的是通过特定类型的电路以使网络正常运行，这种类型的规划应用了一些简化[8-9]，例如，电压幅值限制被忽略，尽管其在短期规划中是必要的。即使应用了一些简化，但是对于各种现实生活中的系统，问题仍然很复杂。

在技术文献中，直流模型和输电模型是解决输电网络扩建规划问题的常用静态数学模型[10-11]，但这些模型只考虑了输电线路和传统变压器的添加。文中提出了一种改进的传输扩建策略模型，该模型考虑了一种新的交流输电系统（Flexible AC Transmission Systems，FACTS）装置。关于FACTS 装置使用的文献非常广泛。然而，大多数论文只讨论了使用FACTS 设备的操作改进[12-13]。文中利用FACTS 设备对有功潮流进行重新分配，以消除拥塞问题和优化电力调度。移相器(Phase Shifter，PS)被认为是一种FACTS 装置，具有重新分配有功潮流的特点。文中在静态集中式规划模型下，分析了在长期输电扩建规划过程中采用电力系统作为备选元件的可行性，该模型可以推广到多阶段规划和有安全约束的规划。输电网络扩建规划数学模型是在直流模型的基础上提出的，直流模型是规划问题中最常用的模型。

1 方法论

1.1 经典模型

当仅考虑输电线路和常规变压器的安装时，输电网络扩建规划问题直流模型的数学表达式[14-15]为:

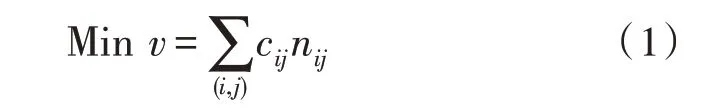
其满足以下约束条件：

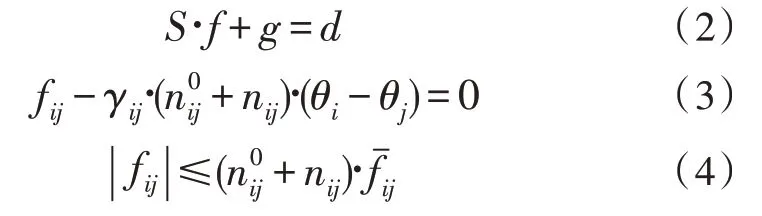
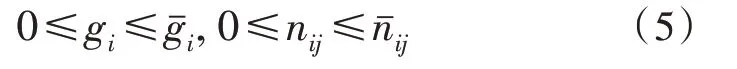
目标函数（1）中，v表示在指定的规划期限内新建输电线路而产生的投资成本；cij表示可加在路径i-j中的电路成本；nij表示在路径i-j中加入的线路数量。式（2）中，S表示系统的节点分支转置关联矩阵；f表示由元素fij组成的有功潮流；d表示总线需求。式（3）中，γij表示路径i-j中一个电路的电纳；表示路径i-j中的初始线路数量。约束条件（2）表示基尔霍夫电流定律（Kirchhoff’s Current Law，KCL）（每条母线一个约束）；约束条件（3）表示基尔霍夫电压定律（Kirchhoff’s Voltage Law，KVL）（每条支路一个约束）。在该模型中，输电线路或常规变压器由决策变量nij表示。约束条件（4）是指传输电路(线路或变压器)的容量要求，因为功率流可以双向流动。约束条件（5）表示生成总线的限制及每个候选路径i-j处新增电路的限制。

1.2 带移相器模型

在输电网络扩建规划问题中考虑移相器时，直流模型采用以下形式：

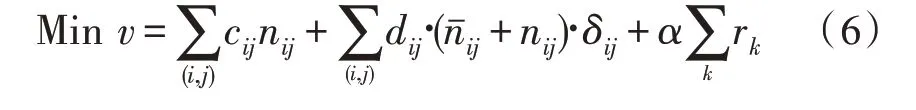
约束条件如下:

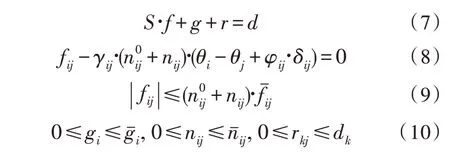
目标函数（6）对应于投资成本。S·f、g分别指由于插入输电线路和移相器而产生的成本，r指由于人工生成的存在对所分析配置的惩罚。

在一条或多条线路上安装移相器可以表示为母线角度和设备提供角度的组合。输电线路的端电压之间的夹角可以通过安装移相器来修改。当插入这些设备时，功率流方程(KVL)会受到影响。因此，移相器的功能出现在KVL 中，它对有功功率流进行了重定向。

移相器被认为是一个电抗可忽略的元件，可以与输电线路或常规变压器串联[16-18]。文中移相器的角差被认为是一个无界变量，但是，可以在不显著修改数学模型的情况下设置限制。在式（8）中，变量δij的存在使该关系相对于直流模型更加具有非线性，其中，δij=1 表示路径i-j中存在移相器，δij=0 表示路径i-j中存不在移相器。

约束条件（9）、（10）分别为电路的传输容量以及发电总线的限制、在每个候选路径i-j中添加的电路限制和人工生成总线的限制。因此，由于移相器的特性，文中提出的数学模型比经典模型更为复杂[19]。

在传统模型中，路径k-m中的输电线路如图1所示。在路径k-m中，移相器被认为是与输电线路或常规变压器串联的零阻抗元件，如图2 所示。当选择一个路径k-m时，移相器被分配给路径k-m中存在的每条输电线路。因此，每个选定路径上的移相器数等于移相器既可以分配到现有输电线路上，也可以分配到优化过程中创建的输电线路上。目标函数（6）与约束条件（7）-（10）表示一个MINLP，它比模型（1）-（5）更复杂。

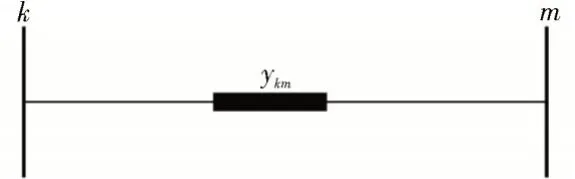
图1 输电线路

图2 输电线路和移相变压器

1.3 三总线系统示例

为了说明移相器的应用，给出了一个由三条总线组成网络的实例，如图3 所示，由该三总线系统执行线性化直流功率流。

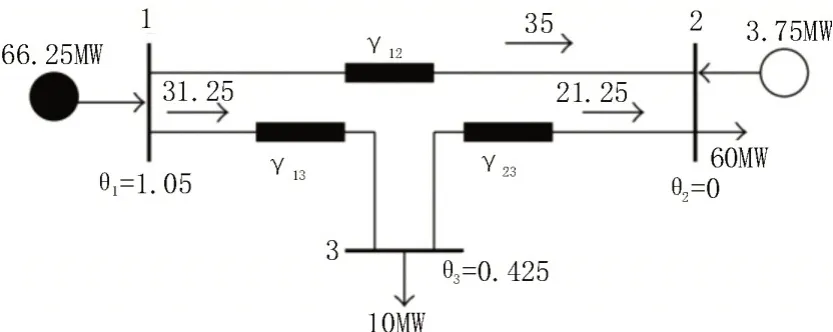
图3 三总线系统

需注意的是，总线2 处存在r2=3.75 MW 的负载减少。因此，该系统运行不充分，需要新的输电线路；另一方面，1-3 号总线和2-3 号总线的运力不足。在不使线路1-2 过载的情况下，不可能增加通过线路的传输功率。对于这个问题，一个解决方案是在1-3 总线处安装一个移相器，如图4 所示，这样系统就可以在不减少负荷的情况下运行。因此，这个例子显示了一个移相器可以重定向有功功率流，这一特性将用于长期输电规划。

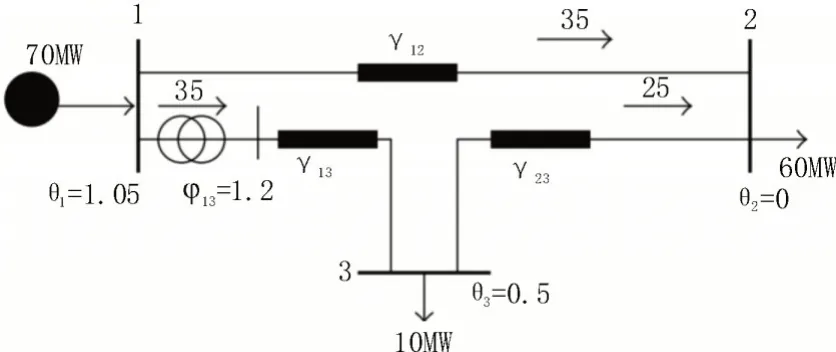
图4 带移相器的负载流解决方案

2 遗传算法

元启发式算法特别适用于搜索空间大且有许多局部最优的问题，如输电网络扩建规划问题。与传统模型相比，基尔霍夫电压定律问题的非线性程度更高。模拟退火算法、遗传算法、禁忌搜索算法等都是解决这类问题的有效方法。文中采用了一种改进的遗传算法来求解数学优化问题。实际上，为了保证遗传算法的可接受性能，需要进行额外的修改。下面介绍考虑添加移相器的规划问题的遗传算法。

2.1 编 码

群体中的每一个个体（染色体）都是这个问题的解决方案。在这项工作中，只考虑整数和二进制变量。剩余变量（连续变量）由线性规划解获得。因此，输电线路和变压器用十进制编码（变量nij）表示，而移相器用二进制变量表示(δij)。

长度为2nl的染色体示例如图5 所示。第一个nl位置表示为每个配置添加的输电线路的数量，最后一个nl位置表示在每个路径中添加了移相器。现有的输电线路没有编码，但在计算操作变量以及在每条路径上向输电线路串联添加移相器时，都会考虑到编码。可以看到，在路径2 中，添加了两条输电线路和相应的移相器。在路径3 中，添加了一条输电线路和必要数量的移相器，以此类推。

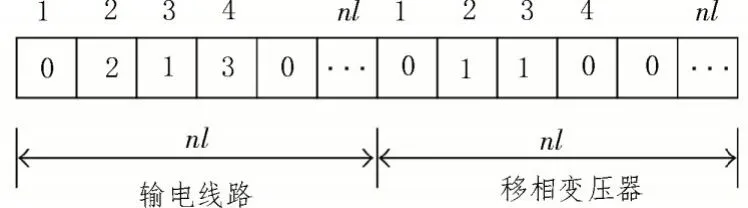
图5 编码方案（染色体示例）

2.2 目标函数与不可行性

任何解决方案的目标函数都是通过求解一个线性规划问题得到的。线性规划确定操作变量的精确值，这使得验证所确定的投资方案的操作可行性成为可能，即系统是否对已实施的扩建方案进行减载。

在遗传算法中，考虑了各种解决方案。不可行的配置(带有减载)通过选择过程逐渐消除，因为这些配置受到目标函数中参数α的惩罚。

2.3 选择过程

选择基于k=2 的锦标赛，即当前人口的两个拓扑参与的博弈游戏。最近的研究表明，只要参数k设置适当，锦标赛选择是解决带有惩罚的目标规划问题最有效的方法[20]。

2.4 交 叉

文中采用单点交叉法。交叉点是随机选择的，并创建一个后代，它有一个来自交叉点的父代。随机点是从1 到nl-1 的区间产生的，即只考虑染色体的前半部分。在染色体的后半部分中，执行相同的操作，如图6 所示。该操作的目的是将存在于染色体两个区段中的现有信息仅传送给一个后代，以避免质量退化。

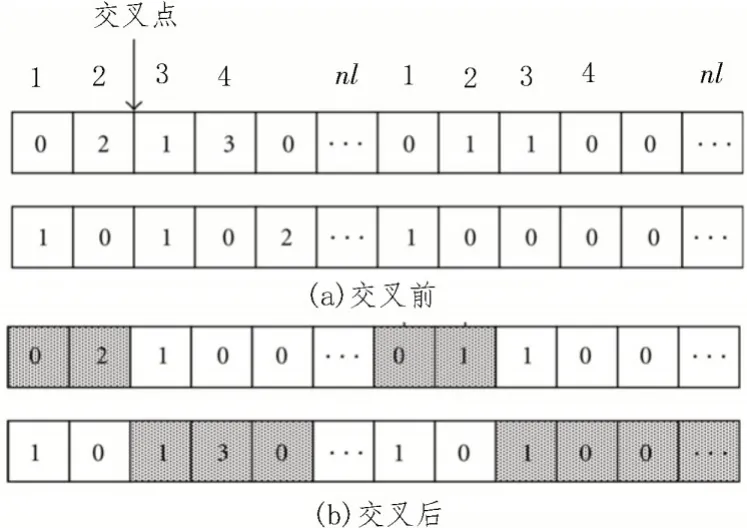
图6 单点交叉

2.5 突 变

对于输电线路，突变操作的应用意味着在优化过程中增加或删除一条输电线路(nij+1 或nij-1)。对移相器来说，它意味着一个等位基因的改变，即在路径中包含或排除移相器。

突变操作在以下条件下执行：

1）路径中输电线路达到最大数量。

2）在所选路径中添加移相器之前，必须检查是否存在输电线路；如果是空路径，必须添加输电线路。

3）当输电线路被移除时，相应的移相器被移除（若存在）。

综上所述，移相器只能插入到现有的输电线路中，而移相器的数量等于支路中输电线路的数量。图7 中给出了两种突变的情况。第一种情况是在现有的输电线路上随机添加移相器；第二种情况是对被删除的输电线路进行变异操作（在这种情况下基本拓扑中没有输电线路），然后去掉移相器，以保持过程的一致性。

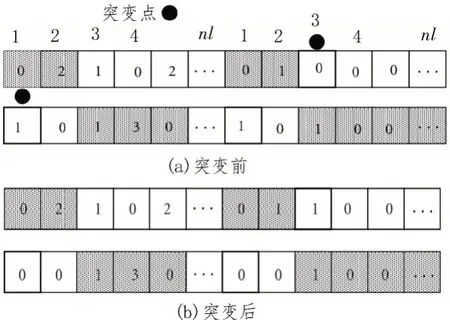
图7 突变

2.6 遗传算法基本流程

所实现的遗传算法的基本流程如下：

1）设置控制参数并生成初始种群，使初始种群为当前种群。

2）通过为当前种群的每个元素(拓扑)求解一个线性规划来计算当前种群的目标函数，尽可能更新现有解决方案。

3）如果满足停止标准，则停止该过程，否则转至步骤4）。

4）通过k={2；3}的锦标赛执行选择。

5）执行单点交叉。

6）实施突变。

7）形成当前种群并转至步骤2）。

2.7 遗传算法的细节和改进

下面简要介绍算法的细节和对遗传算法的一些改进。

2.7.1 初始种群的产生

初始种群的产生是通过一个受控的随机过程进行的，它定义了添加输电线路的路径数和最大移相器数。对于输电线路，随机定义了插入输电线路的支路数、位置和输电线路数（受添加线路的限制）。在存在移相器的情况下，支路的数目和位置是随机选择的。一般来说，根据输电规划经验，需要增加的支路数量应该少，而移相器的支路数量应该更少。

性能系数可用于对最感兴趣的输电线路进行排序，如式（17）所示，具有更大容量且具有成本效益的线路在添加中具有优先权：

2.7.2 控制参数

采用的交叉率为RC=0.8，两种突变率分别为RM=0.1 或RM=0.6(突变率值取决于当前的种群多样化水平)。突变率的定义不同于经典的概念，它适用于一个完整的解决方案(拓扑)。例如，突变率为0.1意味着拓扑发生变异的概率为10%。种群大小从40到200 个元素不等。

3 应用测试

为了验证提出的遗传算法的适用性和优势，并利用移相器证明该数学模型的可行性，文中选取IEEE-24 总线可靠性测试系统进行计算分析。该系统由38 条输电线路和32 台发电机组组成，其中17条总线承载负荷，总负荷值为2 850 MW。系统分为北区230 kV 和南区138 kV，由五个变压器支路连接。文中拟选的可建线路包括38 条原输电线路和50 条待选线路，系统的38 条原始输电线路的编号从1 到38。

为了验证算法性能的改善，分别采用提出的遗传算法和改进Benders 分解算法[3]进行实验。算法参数设置相同，最大迭代数为200，年度最大负荷利用小时数为5 000 h。所有测试都是针对具有非真实成本值的移相器进行的，目的是从理论角度测试将此类设备建模为电气系统扩展组件的可行性。

图8 显示了使用遗传算法和改进Benders 分解算法迭代总数的比较。

图8 迭代次数对比

从图8 可以看出，使用遗传算法的迭代次数更少，前50 个episode 的总迭代次数减少了30%，这验证了遗传算法的性能优越性。

由于不进行扩建规划，网络无法满足要求，可靠性和灵活性很差。因此，需要对原有的网络结构进行扩展，以提高系统的可靠性和灵活性。为了与传统规划算法进行比较，文中规划了两种不同的方案，规划方案按照线路建设顺序进行排序，如表1 所示。这两种方案都是通过遗传算法得到的，两种方案的规划如图9 所示。

表1 IEEE-24总线可靠性测试系统规划方案比较

从图9 可以看出，两种方案只有一条相同的线路，即7-8 号线。方案二主要集中在北部地区内部和南北地区之间的电力交换，南区仅增加7-8 线，以确保系统满足约束条件。方案一主要是加强南北地区内部的电力交流，在北部地区的右侧母线之间增加了三条输电线路，在南部地区的右侧和2-9 母线之间增加了几条输电线路。

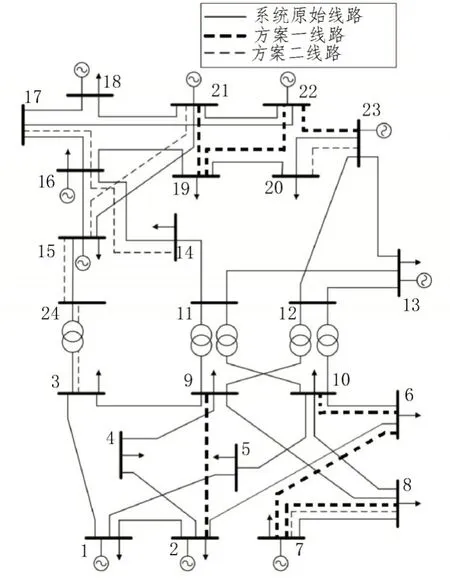
图9 两种方案的规划

为了验证故障后潮流分配的改进，文中比较了不同线路切割后的网损，如图10 所示。可以看出，线路故障后，方案一的网络损耗一般较小。因此，方案一的结构潮流分布更加合理可靠，根据需求进行潮流调整的空间也更大，证明了方案一具有更好的可靠性和灵活性。

图10 切断不同线路后的网络损耗比较

对IEEE-24 总线可靠性测试系统的实验表明，所提出的遗传算法不仅能很好地完成规划，而且能实现扩展方案的灵活调整。

4 结束语

目前，FACTS 器件等现代元件在输电系统中发挥着重要作用，在这种情况下，将这些设备与经典元件结合起来对于输电网络扩建规划是非常重要的。因此，文中提出了一种将移相变压器纳入输电网络扩建规划数学模型的新方法。该模型比直流模型更为复杂，然而，遗传算法很好地解决了这一问题。实验结果表明，提出的算法具有良好的模型一致性和较高的性能，这一贡献将扩建规划问题中经典组件的使用扩展到了现代元素。