基于改进委托代理模型的关键链项目缓冲确定方法
张俊光,王美华
(北京科技大学经济管理学院,北京 100083)
项目自身和所处环境不确定性增加了项目延期和超支风险,关键链项目缓冲的合理设置能有效降低这种风险。关键链方法将约束理论引入到项目管理领域,通过设置缓冲管理项目进度,弥补了关键路径等方法不足[1]。在剪切粘贴法(cut and paste method,C&PM)[1]和根方差法(root square error method,RSEM)[2]基础上,已有方法侧重从项目属性和自身不确定性等角度确定缓冲。然而,现实中项目往往是在某特定情境中展开的,项目人员心理行为等内在特征同样会影响缓冲大小。同时,项目主管和员工间存在典型的委托代理关系。信息经济学将拥有更多私人信息的参与人称为“代理人”,拥有较少甚至不拥有私人信息的参与人称为“委托人”[3]。在项目计划阶段,员工向项目主管上报活动工时,主管根据员工提供的信息对活动工期进行处理并抽取安全时间。由于员工上报工时的真实性和准确性难以保证,双方信息不对称易导致员工产生机会主义行为。为避免此类现象,已有研究从组织行为学角度证实,信任这一内生激励方式能有效促进员工绩效,表现更高的努力水平[4]。此外,根据领导者成员交换理论,领导者由于精力或资源限制对不同下属采取不同态度,对高质量“圈内”员工更为信任,对低质量“圈外”员工的信任仅存在于契约约束信任,上下级存在较为明显的垂直纵向联系[5]。在关键链特定项目管理背景下,现有研究对员工和主管间信任差异考虑不足,导致主管抽取的安全时间和确定的缓冲存在偏差。
鉴于此,本文结合员工与主管间纵向信任关系对经典委托代理模型进行改进,以双方收益最大为准则确定员工实际努力水平,即员工实际总产出,进而求得活动安全时间,建立新的缓冲确定模型。研究贡献主要包括以下几点:第一,考虑了纵向信任对员工上报工时的影响,项目主管根据与各员工不同信任水平可降低其对员工的认知偏差;第二,引入委托代理模型,采用信任系数对员工实际努力水平进行优化,以确定基准工期,避免了原有方法以活动工期一半为基准工期的不足;第三,以双方收益最大为
1 文献综述
基于两种经典缓冲确定方法[1-2],学者从项目属性和不确定性等方面对缓冲确定方法进行了改进,少数学者从人员心理行为因素等角度加以研究。考虑项目属性的研究中,Tukel 等[6]分析活动逻辑关系和资源约束关系,但未综合考虑两种属性对缓冲的影响。Wang 等[7]考虑活动级别及目标,建立了基于换算系数的缓冲确定方法。Zhang等[8]分析信息传递对缓冲的影响。考虑项目不确定性的研究中,Iranmanesh 等[9]考虑环境或工序风险、限制性资源和工序位置等提出了基于后密度因子的缓冲确定方法。尤建新等[10]应用贝叶斯模型管理项目进度。Ma等[11]分析信息流交互风险并优化返工安全时间,提高了缓冲精度。考虑人员心理行为因素的研究中,White等[12]提出项目缓冲设置需考虑行为因素,但其未提供具体缓冲确定方法。施骞等[13]在确定完工保证率时应分析决策者风险偏好,然而其并未实质性探讨人员行为对缓冲确定的影响。
委托代理理论已应用在管理、经济和社会等多领域研究中。在考虑委托代理双方心理行为方面,学者主要考虑了信任、风险感知和过度自信等心理状态。首先,信任可分为个人信任和组织信任,其中,个人信任中纵向信任体现为员工和主管纵向信任关系,研究表明强信任关系不仅能提高工作业绩,还能减少人员欺诈和隐藏信息等行为,即信任能有效提高拥有较多私人信息方行为的可预测性,帮助私人信息更少一方做出较合理行为决策[14]。孙娟[15]采用实验设计方法研究代理人激励合同设计问题。牛建波等[16]从心理学和组织行为学角度研究信任对高管薪酬和公司治理影响。其次,风险感知研究中,如Zambrano[17]讨论在委托人和代理人均为风险中性时是否应开展项目。Sinclair等[18]描述了在委托代理道德风险环境中,委托人为消极风险规避者时,应如何采取措施权衡风险分担与激励关系。最后,在过度自信方面,Adam等[19]在经典委托代理模型中考虑代理人过度自信心理,分析其在该心理状态下的决策偏差。Royal 等[20]研究了生产要素的可获取性如何影响过度自信代理人行为等问题。
综上所述,现有研究对人员心理行为偏好考虑不足,少有学者考虑管理者风险偏好水平,而未分析目标建立缓冲确定模型,确定安全时间和项目缓冲大小,对整个项目工期进行了更加合理地界定。利益相关者其他因素如信任等,增加了缓冲结果误差。同时,委托代理理论能结合心理行为因素分析委托人如何诱导代理人选择对委托人最有利的行为。已有研究考虑了过度自信和风险感知等因素,而将信任引入模型的研究多为质性研究,且未被用来解决缓冲确定问题。因此,本文针对关键链项目缓冲确定问题,在经典委托代理理论基础上,通过信任关系优化员工努力水平,求得不同信任程度下活动工期应抽取的最佳安全时间并建立缓冲确定模型。
2 基于委托代理模型的缓冲确定
为确定项目缓冲,本文首先对所研究问题进行情境描述;其次,按照委托代理模型基本分析框架,将项目中的主管和员工间信任关系引入模型并加以改进,求出员工实际努力水平;最后,依据努力水平确定各活动的安全时间,采用尾部集中法确定项目缓冲。
2.1 问题描述
本文从项目主管与活动各负责人间的纵向角度考虑信任等对缓冲确定的影响。假设某项目考虑资源约束后的链路共包括n项关键活动,每项活动分别对应1位负责人上报工时,即该委托代理关系的行为主体共涉及1 位主管和n位员工,其中,主管为委托人,员工为代理人,双方关系结构如图1所示。
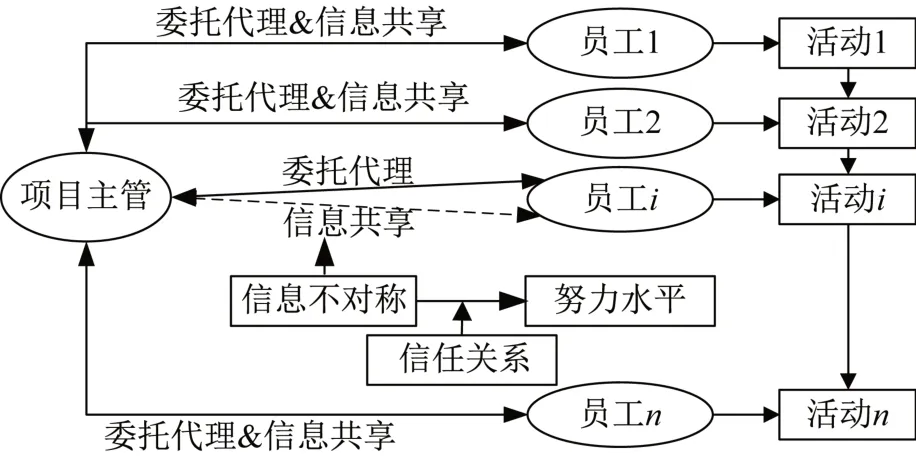
图1 关键链项目中的委托代理关系Fig.1 Principal agent relationship of critical chain project
图1单层委托代理关系中,努力水平是指在保证其他不变情况下,为实现项目目标做出的努力,其结果体现为剔除安全时间后的活动基准工期与单位时间努力产出的乘积。当主管和员工为较强信任关系时,员工结合自身情况上报一个包含安全时间较短的工时,反之,则上报一个包含安全时间较长的工时。因此,主管应充分考虑双方信任对活动时间的心理认知差异,以更合理确定项目缓冲,原理如图2所示。

图2 考虑信任因素的项目活动工期Fig.2 Project activity duration witha consideration of trust factors
2.2 基于信任的委托代理模型建立
本文借鉴相关文献对经典委托代理理论从主管和员工两个角度进行分析[15],根据理论中涉及的核心公式计算参数结果,为确定活动安全时间提供依据。
2.2.1从主管角度分析
设主管和员工均追求自身收益最大,员工越努力,产出越高,且员工在上报工时过程中不存在合谋或恶意等现象。双方间信任指数为ti(0<ti<1),ti表示主管与员工i间的信任程度,是主管根据其与员工i以往项目合作情况事先确定的一个常数值。如在实际项目中,若该员工整体表现业绩较佳,工作能力和风险应对能力较高,信誉以及责任感较强,较少产生工作失误,能按时保质保量完成任务,主管对于该类员工应设置较高信任关系值,反之,则设定相对较低信任关系值,主管与每名员工均存在一个信任关系值,则其与n名员工共具有n个与之对应的信任数值。li为努力水平,是大于零的一维变量,可理解为工作付出努力而带来的产出,反映员工i努力程度,不同努力水平会产生不同努力成本和绩效,则对于主管而言,与员工i考虑信任关系线性产出函数为[15,21]

式中:λi为均值为零,方差为的正态分布随机变量,其包含除员工努力之外不确定因素对产出函数的影响,反映活动外生不确定性,如项目可能面临项目外部市场环境等因素的影响,市场环境等风险作为除员工努力之外的不确定因素,其对产出影响是包含在λi之内的,最终体现为不同方差值值越大表明活动不确定程度越大,本文在仿真部分用不同随机数替代,该值越大,认为市场环境等外生因素对活动影响越大。由于ti和li是在外生不确定因素λi实现之前选择的,即λi与ti和li独立[3]。因此,信任关系和努力水平仅决定产出均值,而不影响产出方差。式(1)产出函数期望和方差为[15]
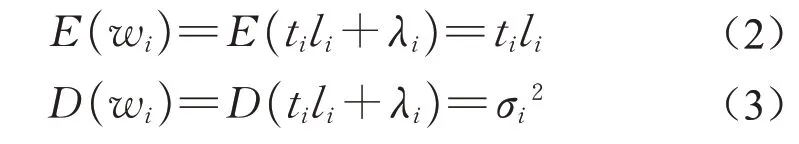
经典委托代理模型假定主管为风险中立型,员工为风险规避型[3]。参考Holmstrom 提出的分布函数参数化方法,主管对员工i委托代理合同为[22]
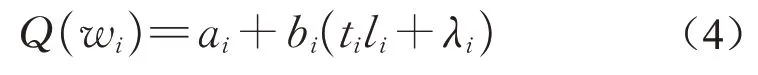
式中:Q为员工获得的总收益;bi为员工产出的分享或激励系数(0<bi<1),也作为风险分担因子,即产出wi每增加一个单位,员工收益增加bi,bi越大,则员工承担的风险越多。由于主管和员工间存在信息不对称,员工易因信息不对称产生机会主义行为。因此,对于主管而言会产生信任成本Ci(ti)。此时,结合式(1)、式(4)和信任成本Ci(ti)的主管期望收益为
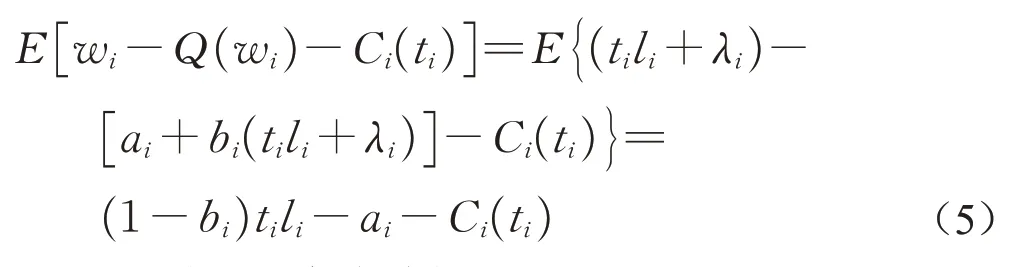
2.2.2从员工角度分析
设员工风险规避特征严格不变,且假定所有收益均可用货币衡量,则员工i风险规避效用函数为[23]

式中:φi为员工i的Arrow-Pratt 风险规避程度,表示当风险损失概率较大时员工会采取措施甚至完全排除风险的可能性,如员工i在面临市场环境等风险时,不同员工风险态度和体现出的风险规避程度也不同,若员工i对市场环境等风险较为惧怕,其风险规避程度φi值更大,反之,则较小,本文在仿真部分通过设置不同大小的随机数,来表现不同风险规避程度,该值较大,员工i对市场环境等扰动因素的风险规避程度较大,反之,则风险规避程度较小;ρi为员工实际收益。由于当员工付出努力时需付出一定代价,即努力成本,当员工付出li努力水平时,对于员工而言努力成本为Ci(li),员工i付出努力越多,其努力成本也随之增多,据已有研究设员工i努力成本为[3]

式中:γi为成本系数,表示增加单位成本效用降低程度,γi越大,同样努力的负效用越大,不同员工成本系数不同,本文采用不同随机数进行代替,以反映员工成本系数差异,员工i付出同样努力为其带来的效用降低程度越大,则该值越大,反之,则越小;li为员工i付出的努力,对员工而言通过风险规避态度和外生不确定因素等进行综合判定,根据式(4)和式(7),员工i实际收益ρi表示为
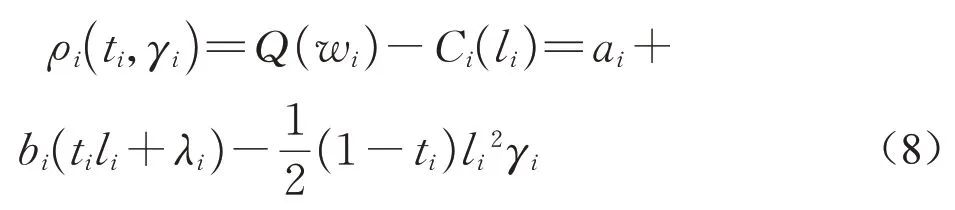
此时,可计算得出员工i的期望收益为
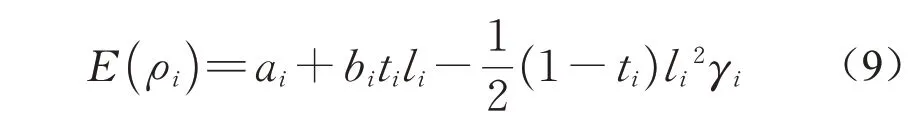
根据确定性等价原理[24],员工i考虑活动不确定性因素成本后获得的确定性等价收益为

设员工i保留收益水平为ρi0,当员工i从委托代理合同中获取的收益水平不低于ρi0时,才会选择接受设定的合同条件。同时,由于主管和员工信息不对称,在激励相容下员工趋于采取自身收益最大的行动[15]。在员工i确定性收益高于保留收益水平ρi0约束下,对其求导得信息不对称下的激励相容条件
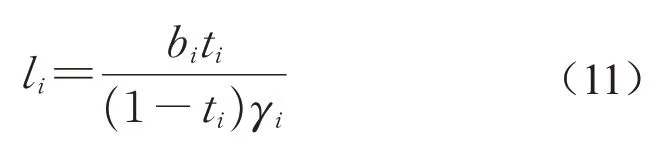
在考虑员工确定性等价收益作为约束条件时,确定性等价原理存在边际效用递减的经济学基本假设[24],主管考虑在员工参与约束和激励相容约束条件下最大化自身期望收益,则主管优化问题为[15]
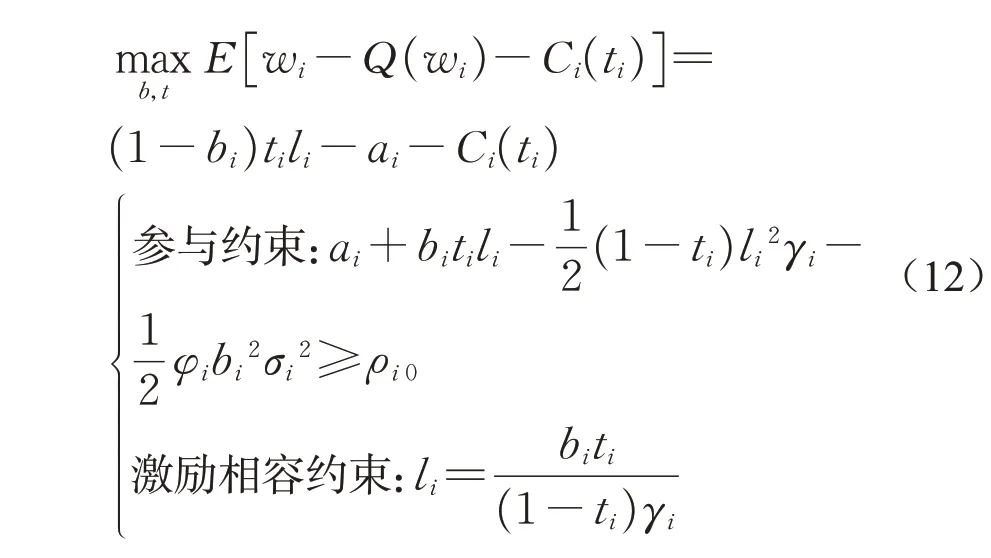
根据式(12)代入激励相容约束后,将约束条件取等,此时可计算ai为
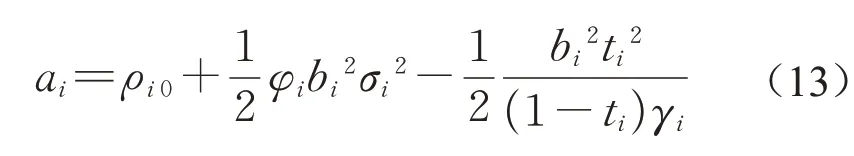
将式(13)代入式(5)中,则期望收益为
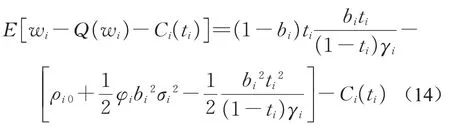
在已确定的主管与员工信任系数ti情况下,该期望收益函数为bi的一维变量函数,且为激励系数满足单调递增凸函数,表示收入与效用边际效用递减关系,且bi二阶导数恒小于零,此时,在bi一阶导数等于零时,求得主管期望收益最大。因此,对式14bi求导,导数为0得主管目标最优时bi
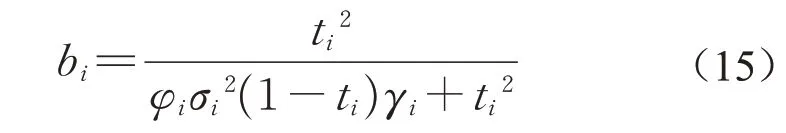
根据主管和员工角度委托代理模型分析,则主管和员工收益最大时员工i实际努力水平li可表示为
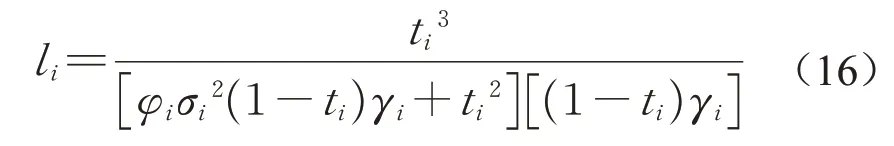
式中:li为员工完成该项活动实际付出的全部努力;ti为主管事先确定的与员工i信任关系值;φi代表员工i不同风险规避值,反映员工风险态度反映活动面临外生不确定性,不同活动取值也不同,值越大,表明该活动不确定性越大;γi为成本系数,值越大,表明员工i为工作付出努力成本消耗和负效用越大。实践中参数根据项目实际情况进行确定,本文用随机数代替各参数来确定员工完成活动实际时间。
2.3 项目缓冲确定
基于2.2节确定项目中n个活动的安全时间,应用根方差法确定缓冲,以应对项目不确定性和保证项目工期[1],原理如图3所示。
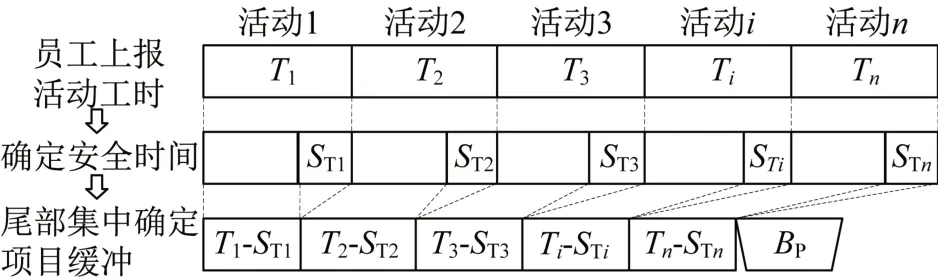
图3 项目缓冲大小确定原理Fig.3 Principle of project buffer size determination
通过主管和员工间的信任关系确定员工的努力水平,并以此指标来计算完成对应活动所需的实际工期,进而确定各活动应抽取的安全时间,关键链上每项活动安全时间为
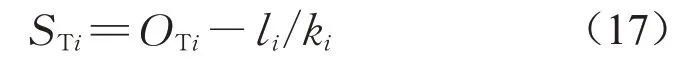
式中:STi为活动i安全时间;OTi为员工上报的原始活动工时;li为员工最终实际努力水平,即为员工为完成该活动而付出的努力水平总量;ki为各员工单位时间预期努力水平,为单位时间量。借鉴根方差法[2],设BP为项目缓冲,则缓冲大小确定模型为

3 算例验证
本文采用某项目进行模拟仿真。已知项目共包括16 项活动(“*”为关键活动),项目基本信息如表1所示,关键链网络图如图4所示。

表1 项目活动基本情况Tab.1 Basic information of project activities
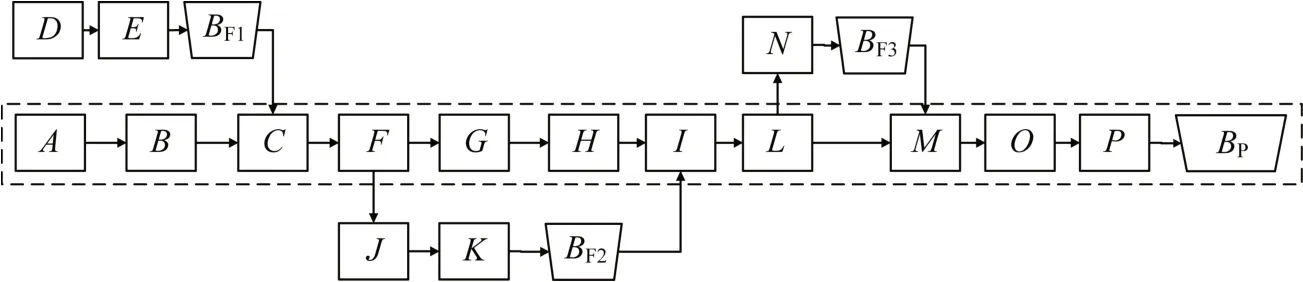
图4 关键链项目网络图Fig.4 Critical chain project network
图4中BF1、BF2和BF3分别为支链上的接驳缓冲,本文假定接驳缓冲能有效保护支链活动,不会影响主链关键活动,关键链路不发生变化且不存在链路断裂等情况。同时,要求项目在特定计划区间内完工且结束-开始的搭接关系不可被中断,结束后开启其紧后活动,直至项目完工。
3.1 实验模拟
本文借助Matlab R2017a 软件中的Monte Carlo模拟技术将缓冲确定试验重复1 000次。Fallah等[25]认为活动工期是服从对数正态分布且右偏的随机变量,即若Y~N(μ,σ2),则X=eY服从对数正态分布,即X~ln(μ,σ2),模拟的均值和方差如式(19)和式(20)所示。

应用Matlab R2017a 软件中对数正态分布随机矩阵函数X=lognrnd(mu,sigma,1 000)来产生每组μ和σ2对应的仿真模拟数据,最终得到所有关键活动的1 000×11 的仿真工期矩阵。实践中数据可通过项目实际情况进行测算,本文在模拟时参数由仿真程序生成的随机数代替,具体参数如表2 所示,并根据2.2节和2.3节公式计算1 000组随机工期的项目缓冲和指标结果。

表2 项目活动具体参数Tab.2 Specific parameters of project activities
3.2 仿真结果
本文从缓冲大小、项目工期、按时完工和缓冲消耗情况等方面,比较本文方法和未考虑信任差异等员工心理行为因素的RSEM法,对比结果如表3、图5、图6和图7所示。

图5 缓冲大小和项目工期对比图Fig.5 Comparison of buffer size and project duration
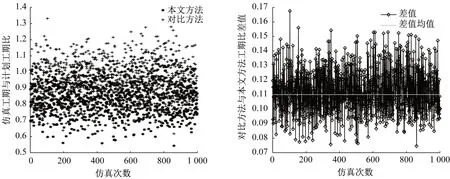
图6 项目仿真工期与计划工期比对比结果图Fig.6 Comparison results of project simulation duration and planned duration
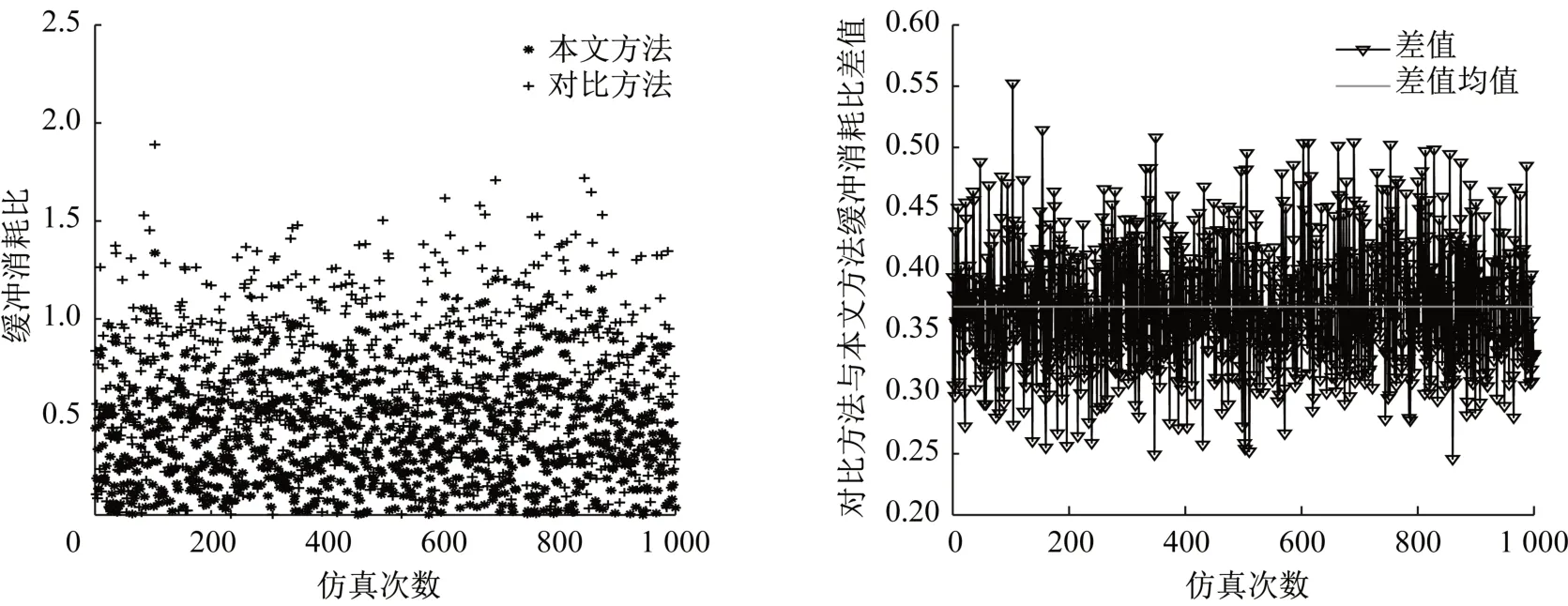
图7 项目缓冲消耗比对比结果图Fig.7 Comparison results of buffer consumption ratio of projects
由表3 和图5 可知,从缓冲大小对比结果上看,本文方法缓冲总体小于C&PM且大于RSEM。缓冲比较可从以下几个方面解释:首先,C&PM对链路上所有活动均采取50%原则确定缓冲,因任务多寡和持续时间长短不同,会致使缓冲呈现线性增长趋势,导致确定的缓冲过大,对项目产生过度保护;其次,RSEM 基于中心极限定理,同样采取“切一半”的方法确定基准工期,据根方差量确定缓冲,当项目风险较小时,RSEM抽出缓冲较大而基准工期较短,导致项目执行困难,而当项目风险较大时,RSEM基准工期较长,此时会因员工学生综合症造成浪费。因此,该方法未充分考虑人员因素,导致缓冲过小,具有一定局限性;最后,本文根据每个活动不同情形分别抽取不同安全时间,信任程度以及风险态度等因素不同,对安全时间抽取的影响程度不同。因此,本文方法充分结合各活动实际情况和员工特性,弥补了其他方法的不足,所确定的缓冲尺寸更加合理。

表3 结果对比信息表Tab.3 Result comparison information
从仿真工期对比结果上看,本文方法工期总体小于RSEM,平均差值约为12d。由于员工所提供的工期并非完成任务实际时长,其会隐藏因心理因素导致的不必要时间。因此,本文方法不仅考虑员工不同风险规避程度,还考虑员工和主管间信任的异质性,因此,该方法项目工期总体低于对比方法。
由表3和图6可知,本文方法得到的仿真工期占计划工期的比例总体低于对比方法,即本文方法较对比方法能够更好地按时完工。根据对比结果,在1 000 次仿真模拟中,本文方法的仿真工期与计划工期之比总体小于1,即数据点基本位于“1”线以下,较对比方法,本文方法结果大多按计划完工,并未发生严重延期。同时,由对比方法与本文方法工期比的差值图可以看出,在每次仿真模拟中,本文方法实际工期占计划工期比例较低于对比方法,即仿真结果位于“0”线以上,且本文方法的按时完工情况优于对比方法均值为11.22%。这是由于本文在对比方法的基础上,考虑了信任关系和风险偏好程度等心理因素对安全时间提取的影响,克服了因过度提取安全时间而导致按时完工率下降和计划重组的不足。
由表3和图7可知,本文方法得到的缓冲消耗比整体低于对比方法,即该方法较对比方法具有更少的缓冲消耗。根据对比结果,在1 000 次仿真模拟中,本文方法的缓冲消耗大多集中于0.25附近,较对比方法,本文方法仿真结果大多按要求完工,消耗了较少的缓冲。同时,对比方法与本文方法缓冲消耗比差值的均值约为0.37,即对比方法平均比本文方法多消耗36.98%的缓冲。这是由于本文考虑了人员心理因素的影响,而对比方法对该方面考虑较欠缺。因此,当对比方法全部按照50%原则抽取安全时间时,会降低项目基准工期准确性,造成项目延期严重、缓冲消耗过大以及计划频繁变更等情况的发生。结合图5和6分析结果,本文方法能够确定更为合理的项目缓冲,降低缓冲消耗量的同时保证项目按时完工。
4 结论
基于主管和员工委托代理关系并考虑双方信任关系,改进经典委托代理模型,抽取安全时间并形成项目缓冲。仿真结果显示,本文方法能确定更合理的缓冲,缩短项目工期并提高按时完工率,是对已有方法的优化。该研究也在一定程度上强调了关键链项目管理过程中人员心理行为因素的重要性。
新方法在实践应用中应注意关键链理论隐含的基本假设,如无里程碑式管理、学生综合症、帕金森定律和提前完工不报告等,应充分意识到项目中人员特性的差异。因此,项目经理在对每个活动抽取安全时间时,要充分搜集资料信息,合理确定各参数值,以免造成结果偏差过大影响决策。研究局限性在于以单任务委托代理关系为背景,而当行为主体存在多任务或多层委托代理时,其心理等因素仍会影响安全时间。因此,下一步应探讨多任务或多层委托代理情况下的缓冲设置问题,并在动态情形下,将缓冲确定和监控综合起来分析。同时,本文未考虑员工间横向信任,并假定员工在上报活动时间时无横向信息交换,分辨是否存在员工合谋而导致的更多安全时间,是今后研究方向。
作者贡献声明:
张俊光:把握文章整体框架,核准文章终稿;
王美华:确定文章逻辑结构并撰写文章。

