消减换道行为影响的换道轨迹规划
李林波,李 杨
(同济大学道路与交通工程教育部重点实验室,上海 201804)
大量研究表明,自动驾驶车辆可以显著地提高交通效率,增强交通安全,缓解或减少交通拥堵。作为支撑自动驾驶技术的重要组成部分之一,换道规划算法为自动驾驶车辆提供一条由当前车道行驶至目标车道的安全及高效的路径。Luo等[1]基于车对车通信,提出动态自动变道机动算法,该算法由轨迹规划算法和轨迹跟踪算法组成。采用基于时间的5次多项式函数对参考轨迹进行建模,以满足自动驾驶车辆的安全性、舒适性和效率要求。Yang等[2]建立了一个动态换道轨迹规划算法,以克服静态换道轨迹规划算法的缺点,该动态换道轨迹规划算法由轨迹决策、轨迹生成和起点确定模块组成。Zhang等[3]引入了长短时记忆神经网络来同时模拟跟驰行为和换道行为。Xie等[4]同样也引入长短时记忆神经网络模型来模拟车辆的换道行为,采用深度信念网络来描述换道的决策过程。Chen等[5]提出了一种基于注意力的分层深度强化学习算法来学习交通中的换道行为。Zheng等[6]基于Frenet坐标系对弯曲的道路进行建模,建立了基于四元贝塞尔曲线和危险场的换道轨迹规划算法。Li等[7]评估了换道过程中遇到的驾驶风险,并基于势场理论分析了不同车辆运动状态下的安全势场的空间分布。Wang等[8]建立了不可避免的碰撞情况下换道车辆的碰撞缓解算法。黄晶等[9]将个性化驾驶风格融入自动换道轨迹规划算法中。
虽然现有的研究已取得了丰硕的成果,但这些运动规划算法往往忽略了周围车辆的利益。尽管换道车辆可以安全高效地完成换道行为,但可能会对周围车辆,特别是目标车道上的尾随车辆产生不利影响。这些影响反映在实际驾驶环境中,则是微观层面上每辆车的各种成本(效率、舒适度和安全性)以及宏观层面上形成的交通冲击波(降低车速,影响流量)。这些负面影响往往在换道区域内引发低效的交通流或者是幽灵堵塞的出现[10-11]。
本文旨在构建一种面向帕累托最优的换道运动规划算法,主要由以下3部分组成:引入5次多项式模型构建车辆横向以及纵向的轨迹;引入IDM(intelligent driver model)模型来表征周边车辆的跟驰行为;构建各车各时刻的舒适、安全以及效率损失函数,从而建立针对换道车辆与周边车辆损失的多目标优化问题。
1 数学模型
1.1 轨迹规划模型
研究假设车辆已经做出了换道决策,并即将执行换道行为。选择解析式法构建车辆的换道轨迹,这是考虑到数据驱动法的建模过程本质上是一个黑箱,同时车辆和道路的势能场尚未统一,这两种方法在实际应用中会受限于数据集,难以适应各式复杂交通场景,而基于解析式法的换道运动规划算法能够适应各种场景,同时有着很强的可解释性,因而本文引入5次多项式函数构建换道车辆横向及纵向的轨迹[9],其形式如下:

式中:xLC(t),yLC(t),θLC(t)为车辆横向、纵向位置与方向角。ai,i=0,1,...5与bj,j=0,1,...5 则是相应的系数。
理想情形下假设车辆在换道起点与终点的纵向速度和纵向加速度均为零,可得到如下约束:

1.2 IDM模型
引入IDM 模型[14]表征周边车辆的驾驶行为,其形式如下:


1.3 多目标优化模型
假设t时刻,目标车道后方有n辆车(由近到远被标记为1~n)。优化目标主体包括换道车辆与后方车辆。优化目标函数包含舒适、效率和安全部分。引入加速度的一阶导数量化每辆车的舒适度,当前速度和期望速度之差被用来描述效率;相对速度和与前车的相对距离被用来量化驾驶风险,第i辆车在时刻t的3种成本如下:
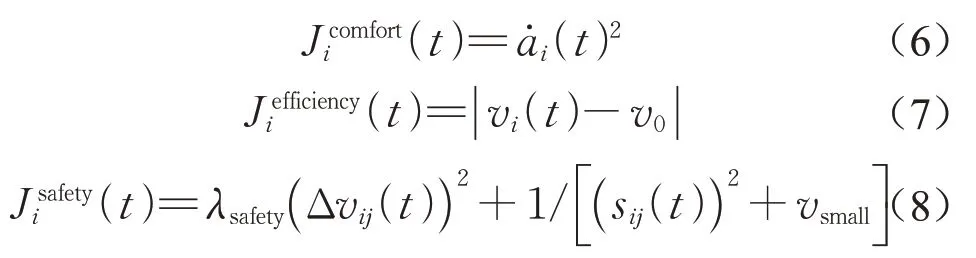
换道车辆的总损失定义如下:

式中:JLC代表换道车辆的损失。Ncomfort,Nefficiency和Nsafety是目标函数中相应项的归一化值(以使单位一致)。ωcomfort,ωefficiency和ωsafety表示舒适性、效率和安全性的权重系数。
后方车辆的总损失函数定义如下:

式中:JTF代表目标车道后方车辆的总损失;ωi代表车辆i的权重系数。对于距离近、相对速度差大的车辆,它们受换道行为的影响越大,其在目标函数中的权重系数就越大,ωi的定义如下:

在执行换道行为过程中,换道车辆需要满足速度、稳定性、舒适性以及安全等方面的要求,各变量需要在合理范围内变化。

式中:vmin,vmax,amin,amax,jmin,jmax,tLC,min,tLC,max,xLC,min,xLC,max代表车辆最大和最小速度、加速度、加速度导数、换道时长及横向最长移动距离。
2 求解算法
2.1 帕累托解
多目标优化问题中的各个目标之间相互制约,使得一个目标性能的改善往往是以损失其他目标性能为代价,不可能存在一个使所有目标性能都达到最优的解,所以对于多目标优化问题,其解通常是一个非劣解的集合。在存在多个Pareto 最优解的情况下,所有的Pareto 最优解都可被认为是同等重要的,因而需要找到尽可能多的关于该优化问题的Pareto最优解。除要求优化问题的解要收敛到近似Pareto最优域,求得的解也必须均匀稀疏地分布在Pareto最优域上,一组在多个目标之间好的协议解是建立在一组多样解的基础之上。
2.2 NSGA-II算法
引入NSGA-II算法,求解所构建的帕累托曲面。与NSGA的第一个版本相比,NSGA-II算法的计算复杂度更低,引入了拥挤度和拥挤度比较算子以保持种群的多样性,采用精英策略来扩大抽样空间,迅速提高种群水平,该算法共有3个主要步骤:
(1)随机产生大小的初始种群,通过遗传算法的选择、交叉和变异三种基本操作,经过非支配性排序,得到第一代子代种群;
(2)从第二代开始,父代种群与子代种群合并,进行快速非主导排序,并计算每个非主导层中个体的拥挤程度。根据非主导关系和个体的拥挤程度,选择合适的个体组成新的父代种群;
(3)通过遗传算法的基本作用生成新的子代种群,以此类推,直到满足程序的终点。NSGA-II算法的基本过程如图1所示,G代表当前的迭代次数,关于算法的细节可参考文献[15]。

图1 NSGA-II算法流程Fig.1 MAPES of training results of GRU model
3 模型验证及分析
3.1 仿真场景设置
所有仿真均是在Python中实现,并在i9-9700CK 3.6GHz处理器上运行,配备16GM内存和RTX 2070。使用PYMOO软件包中的NSGA-II算法求解多目标问题。仿真步长为0.1s,目标函数中相应成本项的归一化值被设定为:Ncomfort=8m·s-3,Nefficiency=25m·s-1,Nsafety=0.5s-1,la=5m,lb=2m,Ca=2.5m,Cb=1m,vmax=30m·s-1,vmin=5m·s-1,amax=8m·s-2,amin=-8m·s-2,jmax=8m·s-3,jmin=-8m·s-3,D0=3.5m,IDM的参数选自于文献[16]。仿真环境如图2所示,仿真时长为500s,目标车道上共有20辆车(头车速度为25m·s-1),经过一段时间的仿真预热,目标车道上的车辆都保持稳定的跟车距离和速度。假设在第300s,换道车辆在目标车道纵向位置的第10辆车与第11辆车之间,换道车辆前方100m处的两辆车突然相撞,车辆不得不进行换道,并且已经完成换道决策。换道车辆必须在第10辆和第11辆之间的空隙中行驶,换道车辆难以在下一个空隙中执行换道,因为其后面有多车紧跟(换道车辆车速也为25m·s-1)。

图2 仿真场景示意图Fig.2 Simulation scene schematic
3.2 模型对比分析
图3展示了数值仿真的结果,图3a为换道车辆与周边车辆损失的帕累托曲面。由于换道车辆与周边车辆损失函数的量纲是相同的,因而以前沿距原点最近的距离画一个圆,将圆与前沿的交点作为最终最优解。可以看到,在这个方案下,换道区域内(换道车辆与周边车辆)的总损失为28.35,其中换道车辆的损失为5.92,周边车辆为22.43。曲面左侧的点代表换道车辆损失较小但周边车辆损失较大的解集(以换道车辆自身利益最大化),曲面右侧的点代表换道车辆损失较大但周边车辆损失较小的解集(以周边车辆自身利益最大化),这两侧解的总损失均高于本文所采用的最终解,这从图3b中的3条损失曲线可以看出。可以看到,相比于曲面最左侧的解,本文所采用的解所对应的区域总损失由35.07降低到了28.35。图3c展示了所有车辆的横向移动轨迹,图3d为所有车辆的横向车头时距。在经过仿真预热后,20辆车达到稳定跟车时距,车头时距为3.25s。当换道车辆插入至第10和第11辆车时,其换道行为明显地影响了后方的跟车行为。

图3 仿真结果Fig.3 Simulation results
3.3 敏感性分析
为进一步验证算法的有效性,本节对模型参数进行敏感性分析。图4为车辆初速车速和初始距离的敏感性分析,可以看到在不同的参数下曲面的位置有明显的差异。当初始速度从18m·s-1上升到25m·s-1,以及初始距离从60m增加到100m时,帕累托曲面逐渐下移,总成本逐渐降低。
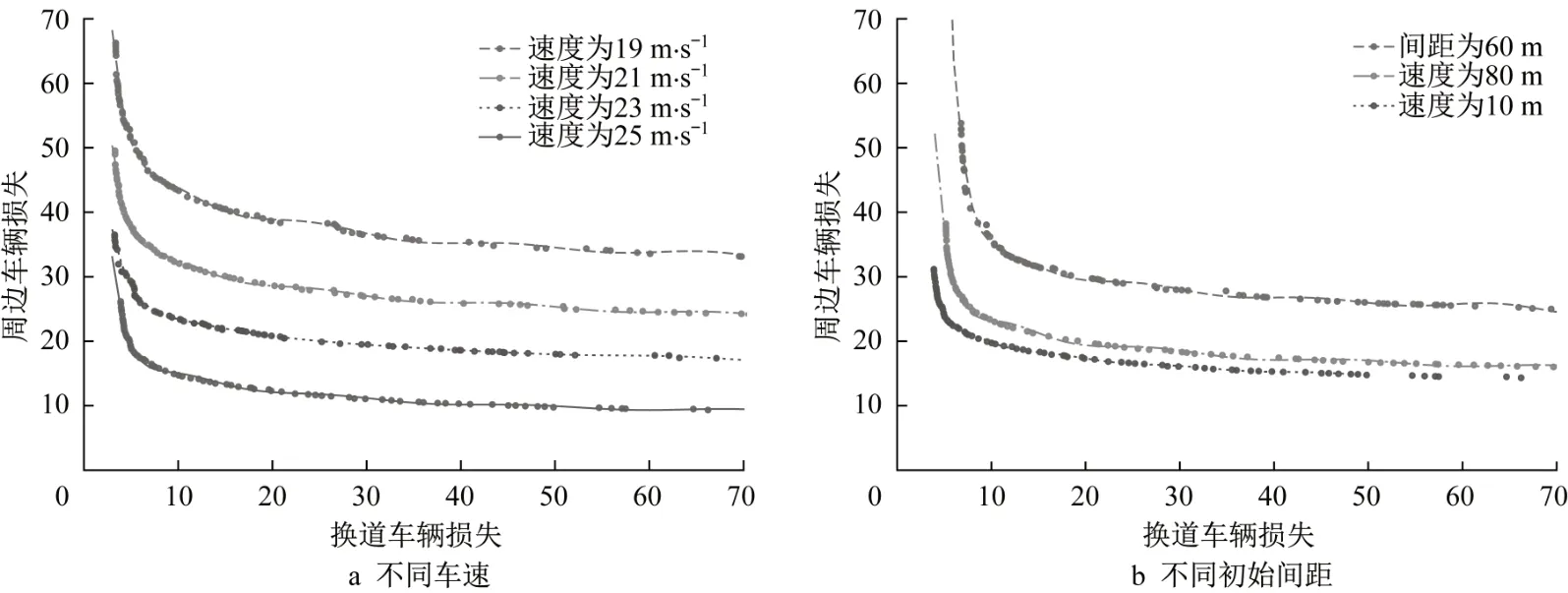
图4 初始车速以及间距敏感性分析结果Fig.4 Initial speed and spacing sensitivity analysis results
此外,本文改变IDM模型中的最小间距和期望车头时距,分析这两个参数的变化对于累托曲面的影响,研究调整静止时的最小间距为7~15m,期望的时间间隔为1s-2.5s,结果如图5和表1所示。随着最小静止间距或期望车头时距的增加,车头时距呈现出逐渐上升的趋势,相应地总损失曲线也逐渐向上偏移。研究结果表明,虽然换道车辆试图使自己的利益最大化,但换道区域内的整体利益不能最小化。而且确实存在这样一个局部最优解,它使该区域的整体损失降到了最低值。

图5 不同IDM模型参数下换道车辆损失、周边车辆损失以及总损失Fig.5 Lane-changing vehicle,surrounding vehicle and total cost under different IDM model parameters

表1 模型对比结果Tab.1 Model Comparison Results
4 结论
本文构建了一种面向帕累托最优的换道轨迹算法,在确保换道车辆能够安全完成换道行为的同时,尽可能降低其行为对于周边环境的影响。基于解析式法和IDM模型构建换道车辆与周边车辆的舒适、安全以及效率的优化目标函数。研究首次将帕累托理念和NSGAII算法引入到换道轨迹规划算法中。实验结果表明,换道区域内确实存在一个帕累托最优解,本文所构建的算法能够有效降低换道区域内的总损失,后续的研究将会去细化本文算法中的损失函数构建,进一步研究混合交通流环境下的帕累托曲面。
作者贡献声明:
李林波:相关概念及方案讨论,论文语言组织;
李杨:概念讨论与模型收集。

