飞行器分支结构局部模态与整体模态的耦合研究

高庆 崔冬玲

（1 中国运载火箭技术研究院，北京 100076；2 淮南师范学院金融与数学学院，安徽淮南 232038）

0 引言

随着运载火箭、飞机等飞行器复杂程度的日益提高，以及结构系统设计和生产水平的提高，飞行器结构与全箭重量的比例逐步降低，内部仪器设备及卫星等有效载荷的重量比例逐步增大，内部仪器设备及有效载荷的动特性对全飞行器动特性的影响也逐步凸显。

航天领域中，常采用子结构综合法或分支模态综合法等[1-2]，开展星箭耦合特性分析，确定星箭界面的载荷和环境等设计条件，用作卫星等有效载荷的设计输入或设计约束；航空方面，也采用子结构方法分析机翼挂载挂架、导弹等外挂物时，全机动特性的变化情况[3]。因此子结构综合法能够解决有效载荷与整机模态耦合的设计问题，但在全飞行器模态试验中，仍然多次发现子结构与全飞行器的模态耦合现象，例如于海昌[4]利用模态试验和建模分析等方法，研究了发动机及支架等局部模态对二级火箭的影响；吴素春等[5]在CZ-2F全箭模态试验中，发现由于载人飞船的模态频率比较低，飞船与火箭之间产生了模态耦合，箭体为二阶振型模态，但飞船与整流罩的振型分别为同向和反向；王建民[6]在某飞行器模态试验中，发现由于某仪器设备的安装频率与全弹一阶模态耦合，产生了两个类一阶振型，并利用理论分析方法进行了简要的解释和说明。金晶[7]、王亮[8]等继续研究了内部分支结构的动力学建模方法，以及对全弹模态参数的影响，但没有关注内部分支结构局部模态与整体模态的耦合问题。本文针对复杂飞行器内部分支与整体耦合问题，基于子结构思想，提出了整体与局部统一的耦合动力学系统的简化模型，利用理论分析方法，研究了内部分支结构的局部模态参数对整体模态频率、振型等的耦合特性，结果表明：局部结构与整体发生模态耦合的必要条件为局部频率与某阶整体模态频率接近，且局部结构对该阶广义质量的贡献较大；振型耦合度与频率比和广义质量贡献度相关，频率变化率与振型耦合度、频率比和广义质量贡献度相关。

1 耦合动力学系统

当局部结构的模态与整体模态接近时，将产生模态耦合情况，根据模态综合法，该耦合动力学系统，可以简化为两个独立系统的叠加，以无阻尼情况为例。

图1 耦合系统的示意图Fig.1 The sketch of coupling system

根据结构动力学中模态频率的瑞雷-李兹计算方法，各状态的模态频率为

综合上式，可得

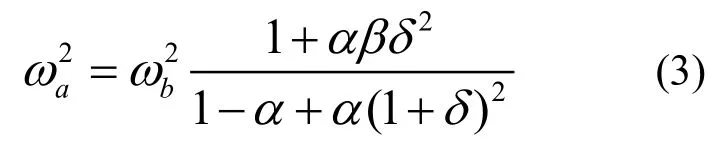
式中，α的含义为不考虑局部模态时，局部结构对整体广义质量的贡献度，其与局部质量成正比，与安装处的整体模态振型平方成正比，但必然小于1，简称为广义质量贡献度；β的含义为局部结构固支约束状态的模态频率，与不考虑局部结构模态影响时的整体模态频率的比值的平方，表征了局部结构模态与某阶整体模态的接近程度，简称为频率比；δ的含义为局部结构固支状态的模态振型，与不考虑局部结构模态影响时，安装基础处整体振型之间的比值，简称为振型耦合度。把频率变化率定义为模态耦合对整体模态频率的影响，是指考虑局部结构模态耦合时某阶整体模态频率aω，与不考虑局部结构模态耦合时该阶整体模态频率bω之间的比值。

2 耦合系统的动特性理论分析

根据瑞雷商的极值性质，式(3)可转换为求解关于δ的极小值以确定δ以及的值，即

可得

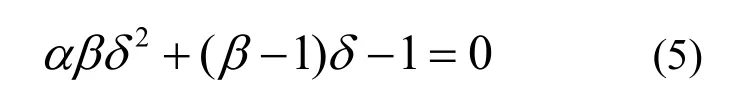
则

代入可得频率为：

当1β=时

当1β≠时

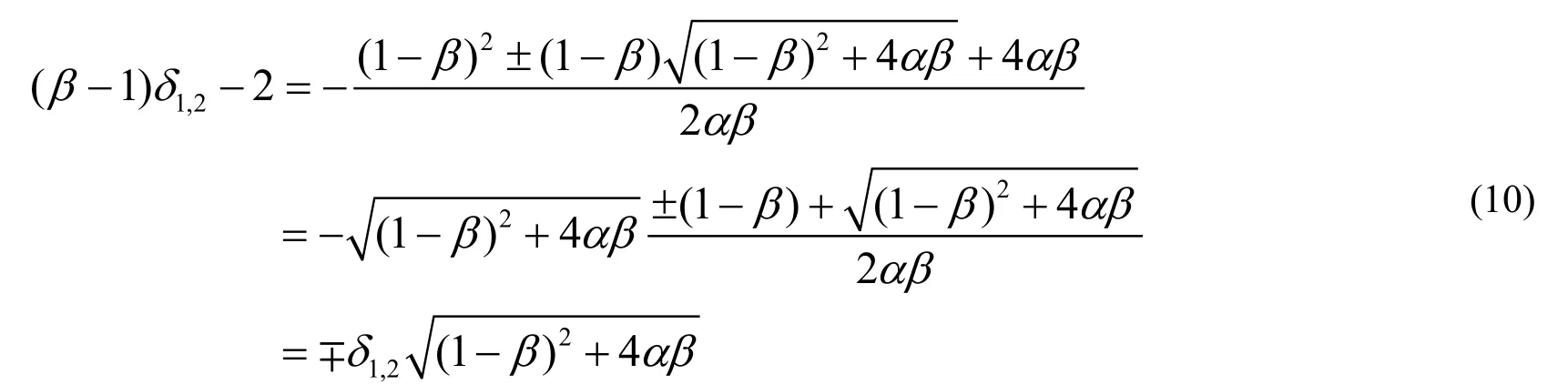
将式(10)代入式(7)，可得

各种耦合情况如表1所示，典型状态振型耦合度和频率变化率的变化情况见图2和图3。

在耦合频率点附近，整体模态和局部模态的振型耦合度幅值相同，但符号相反，整体模态和局部模态频率将发生突变，甚至难以区分整体模态和局部模态；同时广义质量贡献度越大，频率变化率和振型耦合度越大，耦合效应就越显著。因此，为避免局部模态与整体模态发生耦合，最佳途径为调整局部结构的局部频率，并降低局部结构的广义质量贡献度。根据式（6）、（8）、（9）、（11）及图2和图3，可见局部结构与整体发生模态耦合的必要条件为局部模态频率与整体某阶模态频率接近，且局部结构对该阶广义质量贡献度较大，振型耦合度与频率比和广义质量贡献度相关，频率变化量与振型耦合度、频率比和广义质量贡献度相关。

综上，可以利用整体和局部结构的模态参数预示模态耦合的程度，也可利用耦合模态的频率和振型参数，分析确定局部模态与整体模态之间的关系，达到定位局部模态的目的。

表1 局部模态与整体模态的耦合规律Table1 The coupling relationship between local and global modal

图2 典型情况下耦合频率随频率比的变化Fig.2 The relationship between coupling frequencies and frequencies radio

图3 典型情况下振型耦合度随频率比的变化Fig.3 The relationship between coupling mode and frequencies radio

3 典型耦合系统的数值分析

对于大部分飞行器的工程实际情况，可以利用典型梁模型来举例说明。某梁模型全长5m，重量为600kg，质量均布，在0.5m处安装有20kg的设备，可以利用有限元数值分析方法，研究该设备安装模态与整体模态的耦合情况，有限元分析该设备对整体一阶弯曲模态的广义质量贡献度为α=0.03。图4给出了该结构的简化模型，分别为：（a）考虑设备局部安装模态的耦合模型、（b）不考虑设备局部安装模态的整体模型以及（c）设备局部安装的局部模型，与图1及式（1）相对应。可以通过调整设备局部安装频率，研究确定局部模态频率对整体耦合模态频率和振型的影响（图5、表2）。

表2的数值和理论分析结果对比表明，数值分析结果与理论分析结果基本吻合，且局部频率越接近不考虑局部安装结构的整体频率，则耦合状态频率的变化越大，同时耦合状态反映全局特性的模态频率分析偏差相对较小，反映局部特性的的模态频率分析偏差相对较大。图5描述了局部模态对耦合振型的影响，可见如果局部模态与整体模态接近时，将产生双模态现象，即两阶模态，除了局部结构的振型差异明显外，其他结构的振型相似度较大，这与部分地面模态试验结果相互印证。综合表2和图5，可见频率比β＞2时，局部频率ωc对整体频率ωb的影响已经较小（约为1%），即局部频率ωc大于整体频率ωb的1.4倍ωb，与半功率带宽概念相吻合。

图4 典型耦合系统的梁模型 Fig.4 The beam model of a classical coupling system

表2 局部模态与整体模态耦合影响的理论和数值分析对比 Table 2 The theoretical and numerical results of coupling between local and global modal

图5 典型耦合系统局部模态对全局振型的影响Fig.5 The influence from local modal to global modal of the classical coupling system

4 结论

本文针对复杂飞行器内部结构与整体模态的耦合问题，基于子结构思想，提出了整体与局部统一的耦合动力学系统的简化模型，利用理论和数值分析方法，研究了内部局部结构的模态参数对整体模态频率、振型等的耦合特性，可得到以下结论：

1)在某些条件下，不引人注意的局部结构，能够与某阶整体模态发生耦合，从而改变该模态的频率、振型等参数；

2)局部结构与整体模态发生耦合的必要条件为局部频率与某阶整体模态频率接近，且局部结构对该阶广义质量贡献度较大；振型耦合度与频率比和广义质量贡献度相关，频率变化率与振型耦合度、频率比和广义质量贡献度相关；

3)为避免局部模态和整体模态的耦合，最佳途径为调整局部结构的频率，并降低局部结构的广义质量贡献度。