基于逾渗理论的液体火箭发动机管路接头密封性能研究

金辉 赵有磊 尚现伟 金平 蔡国飙

(1 北京航空航天大学 宇航学院，北京 102206；2 北京航天动力研究所，北京 100076)

0 引言

液体火箭发动机管路接头的密封问题属于静密封的研究范畴，静密封的定义为密封界面不存在明显的相对滑动运动[1]。密封部位发生泄漏将给火箭带来巨大安全隐患，2010年发现号航天飞机的氢燃料排放管路发生泄漏导致发射推迟[2]。发动机中的涡轮泵端面密封、阀门、管路接头和法兰等零组件中采用了静密封方式来阻止介质发生泄漏。在预紧力的作用下，如图1所示的待密封两表面之间发生接触，从而形成静密封区域。液体火箭发动机的静密封结构面临着诸多挑战：密封部位处于多场耦合作用状态，介质温差大、压力高和结构振动等[3]，这些复杂的载荷条件加剧了发动机静密封失效的风险。

图1 液体火箭发动机的静密封结构[4]，1-法兰端面,2-垫片,3-接头体,4-螺母,5-接头,6-活门,7-静环, 8-垫圈,9-弹簧10-壳体,11-活门 Fig.1 Liquid rocket engine turbo pump components and valves

大量研究对静密封结构的接触过程开展数值计算和试验，获得密封面的接触压力、接触面积和接触长度，并且以此作为密封性能判断准则。韩冲[5]对火箭发动机60°球形管路接头的静密封进行研究，分析了密封面宽度、平均接触压力与拧紧力矩之间的关系。进一步的，杨卓然和Van Zyl G[6-8]等人给出了接触压力和接触长度下限，认为高于下限值才能满足形成可靠的密封。上述的研究都忽略了静密封接触部位的表面形貌，实际上从微观尺度来看，接触面是由许多粗糙峰和凹陷谷构成的不规则粗糙面[9]，从微观角度进行静密封的接触分析有助于进一步提高对静密封形成过程的理解。闫洋洋[10]采用多尺度有限元模型分析了卡套式接头在拧紧过程中的密封状态和特性变化。Patel H[11]假设法兰垫片的表面由高度不规则的球形微凸体构成，认为密封性能取决于预紧力、流体压力和弯矩等因素。Liua M[12]将静密封两表面等效为刚性表面与分形表面，并以此为基础分析了泄漏机理。在获得各影响因素对静密封性能影响规律的基础上，研究者们希望从形成密封的原理出发，得到满足静密封性能要求的条件。Broadbent S R[13]提出逾渗理论来分析流体介质的逾渗特性，为静密封性能的评价提供理论基础。所谓逾渗是指体系以外的一种介质通过一定的路径进入体系内的过程。该理论与流体自由扩散的区别在于：认为流体的运动不具有随机性，而逾渗结构具有随机性，结构的形状和分布决定了流体的运动方向。Bottiglione F和张彤[14-15]等人认为密封界面并不是光滑的，当粗糙面的接触面积与光滑面的总面积之比（即接触面积比）小于一定比例时就会出现临界泄漏通道。进一步的，史建成[16]利用种子单元扩张的方法，计算得到出现临界泄漏通道的接触面积比值收敛于0.41。Ying Cui[17]建立粗糙表面的有限元接触模型，计算得到整个密封面无泄漏通道对应的接触压力，并将接触压力作为密封性能的评价指标。

液体火箭发动机静密封部位充斥着工况恶劣的流体介质，本文选取发动机中应用静密封形式的管路接头作为研究对象，开展微观尺度和宏观尺度有限元接触分析。首先通过建立静密封微尺度接触模型，得到接触面积比和平均接触压力的关系，然后基于逾渗理论得到微尺度临界平均接触压力（简称临界接触压力）这一性能评价指标，并将应用该指标分析得到的结论和试验进行对比。最后将该指标应用于宏观尺度失效分析的评价当中，分析预紧力、介质压力和材料搭配对管路接头静密封性能的影响，为发动机管路接头的装配与使用提供理论指导。

1 基于逾渗理论的静密封性能分析方法

1.1 静密封表面的形貌模拟

粗糙面的三维形貌是无序的，可以通过统计学方法来描述。提取表面的统计学信息，如形状误差、粗糙度特征和波纹度等[18]，并通过统计学方法拟合出表面形貌。本文参考相关文献[9][18]认为管路接头的加工表面具有各向同性Gauss分布表面特征。构建Gauss粗糙表面的关键步骤是建立Gauss数组内各相邻元素的空间相关性。Gauss数组内每一点高度的概率服从Gauss分布，但这些点在空间上没有相关性，需要依靠构造自相关函数ACF来组成连续的表面，自相关函数描述了随机数组内每一点的空间分布。将尺寸为L×L的正方形区域沿着x、y轴划分为N×N个网格单元，所有单元节点的高度组成服从Gauss分布的二维数组z0，经过式（1）的变换后数组z0成为具有连续性的数组z。

其中z0=θ·randn(N,N)，θ为数组z0的均方根，randn(N,N)为相关性等于0的二维Gauss数组。自相关函数ACF的表达式如（2）所示：

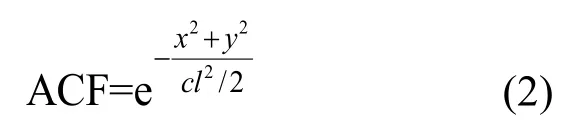
其中x和y为网格单元节点的坐标。cl为相关长度，代表两点相关性。FFT和FFT-1分别为快速傅里叶变换及其逆变换：

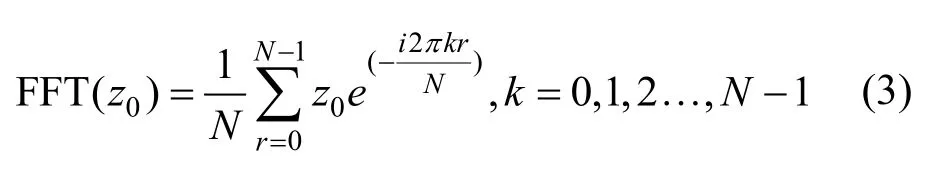
由于FFT对有限数组的变换存在截断误差，需要使用偏态和峰度对求得的随机粗糙表面进行验证。偏态Sk是描述统计分布对称性的指标，Gauss分布数组的偏态Sk=0，这意味着表面轮廓的粗糙峰和凹陷谷均匀分布。峰度Ku是对高度分布曲线振荡程度的度量，Gauss分布数组的峰度Ku=3[23]。

1.2 逾渗理论

在无序系统中，构成系统的各元素之间关联程度变化，引起系统的某一特性发生阶跃，逾渗描述的正是这一阶跃现象[21]。由此可以看出适用逾渗理论处理的系统具有两个特点（1）系统具有随机性（2）系统的元素之间存在某种联系。逾渗理论给复杂、无序空间内的连通性相关问题的研究提供了新的思路。逾渗理论认为固体域的结构形状决定了流体的流动方向，但实际上流体会导致固体域发生微小形变，从而导致流体的流动区域发生改变。当忽略流体域对固体域的作用，逾渗理论可以处理无序系统的连通性问题。

微尺度下静密封的两个接触表面由如图2a)所示的许多粗糙峰和凹陷谷构成，不平整的两表面存在如图2b)所示的黑色接触部位和白色未接触部位，未接触的部位形成空隙，连续的空隙构成了流体介质的泄漏通道，未接触部位的数量越多意味着密封部位发生泄漏的可能性越大，寻找泄漏通道为静密封的性能分析提供了思路。从微尺度观察密封接触面的每一区域，区域内是否发生接触存在随机性，因此静密封满足逾渗理论的假设条件，逐一分析粗糙表面的未接触点就能够判断是否存在连通的泄漏通道。

图2 微尺度下静密封接触部位示意图 Fig.2 Schematic diagram of the static seal contact part at the microscale

将密封界面离散成N×N个如图3所示的正方形网格单元，每一个网格单元只有两种状态，分别是黑色代表的“占有状态”和绿色代表的“空状态”，并且每个网格单元被占有的概率均为γ，则为空状态的概率为1-γ。参考史建成[16]对静密封界面状态演变特性的研究，介质以四连通的方式流动。假设粗糙界面的微尺度接触面积为A，宏观尺度接触面积为An，接触面积比α=A/An,其中α∈[0,1]。当α≈0时，存在贯穿入口至出口的绿色网格单元簇，这意味着界面发生泄漏，而随着α的增大，介质能够流过的绿色网格单元数量不断减少，因此存在临界接触面积αc，当α＜αc时界面不存在贯穿的流动通道。文献[22]中分析了当网格数量趋近于无限大时，界面不存在泄漏通道的临界接触面积比收敛于αc≈0.41。

图3 逾渗理论示意图 Fig.3 Schematic diagram of percolation theory

1.3 静密封性能评价指标

评价静密封性能的指标来源于接触面的信息，包括接触面的应力和长度。接触压力起到构建密封区域的作用，两表面从初始接触到发生挤压变形的过程中接触压力不断升高，一般认为接触压力达到临界值即可满足密封的要求。如图4所示为计算静密封性能评价指标的框架图，在宏观尺度接触部位内选取局部区域作为微尺度的研究对象，找到满足逾渗理论要求的临界接触面积比，然后得到面积比对应的微尺度临界平均接触压力。由于微观尺度模型的面积远小于宏观尺度接触面的面积，可将微观区域视为宏观尺度接触面上的某一点，因此微尺度平均接触压力等于宏观尺度接触面上任意一点的接触压力P，当宏观尺度接触面上某一点的接触压力时，流体介质无法通过该点，考虑到管路接头具有中心轴对称的特征，则该点经过中心轴旋转之后构成了一条阻碍介质泄漏的密封线。

图4 静密封性能评价指标的框架图 Fig.4 Frame diagram of static sealing performance evaluation index

2 静密封有限元接触模型

2.1 微观尺度接触模型

以液体火箭发动机中常用37°DN6球形管路接头作为静密封性能分析的研究对象，选取宏观尺度两接触面的部分区域建立微尺度接触模型，计算微尺度平均接触压力。管路接头的表面粗糙度Ra=1.6um，各输入参数如表1所示。

计算得到粗糙表面的偏态Skz=-0.0052,峰度Kuz=2.9985，与Gauss分布特征表面的理论值相比误差都在1%以内，因此认为生成的随机表面服从Gauss分布。将随机粗糙表面的高度坐标z导入软件Comsol中，通过插值拟合出连续的表面，再经过建模软件的处理得到如图5所示上表面粗糙的长方体。

表1 Gauss分布粗糙面输入参数 Table1 Gauss distribution rough surface input parameters

考虑到接触模型仿真的计算规模，从尺寸为250μm×250μm的粗糙体中截取尺寸为100μm×100μm的区域作为仿真对象。在软件ANSYS中对如图6所示两个表面粗糙的长方体进行有限元接触仿真，上长方体（上体）和下长方体（下体）的材料均为双线性各向同性硬化本构的不锈钢，材料的泊松比υ=0.31，弹性模量E=1.93GPa，屈服极限σs=210MPa，切线模量G=180MPa。采用四面体网格划分，非接触区域的网格单元类型为Solid187，上体的粗糙面作为接触面，单元尺寸为0.7μm，网格单元类型为Conta174。下体的粗糙面作为目标面，单元尺寸为0.9μm，网格单元类型为Targe170，仿真模型的网格单元总数为616997。固定下体的底面，为了使得计算过程更易于收敛，在上体的上平面施加强制位移，上体和下体之间为无摩擦接触，采用无摩擦支撑分别约束上、下体的其它四个侧面。

图5 随机粗糙表面模拟结果图 Fig.5 Random rough surface simulation result

2.2 宏观尺度接触模型

如图7所示为管路接头的结构示意图，由球形接头、接头体和螺母三部分构成，其中螺母对球形接头的后端面施加轴向预紧力，使得接头体和球形接头靠近、接触直至相互挤压。由此可知管路接头的静密封区域是球形接头和接头体的挤压区域，因此在仿真的过程中忽略螺母具体结构，仅保留其预紧功能。如图7所示为管路接头的主要结构尺寸实体图，包括通径d，接头体的锥面角β和球头半径R。

图6 微尺度接触模型及其边界条件 Fig.6 Microscale contact model and its boundary conditions

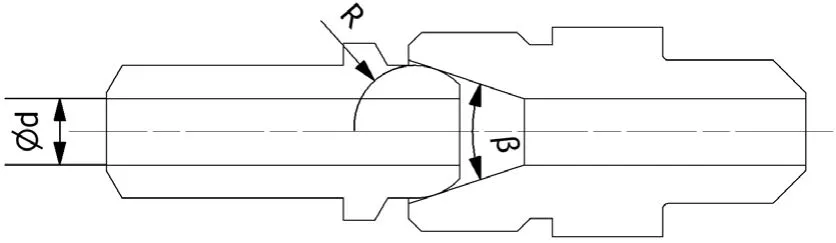
图7 管路接头关键尺寸示意图 Fig.7 Schematic diagram of key dimensions of pipe joint

管路接头在发动机内工作时受到的载荷是轴对称的，因此可将三维模型简化为二维轴对称模型。如图8所示为管路接头宏观尺度接触模型，采用平面单元进行网格划分，非接触区域的单元类型为Plane182，球形接头的球面是接触面，其单元类型为Conta172，接头体的锥面为目标面，其单元类型为Trage169。本文主要关注接触部位的信息，因此对接触部位的网格加密处理，球形接头和接头体的加密尺寸分别为15μm、30μm。固定约束接头体的下端面，在球形接头的左端面施加轴向预紧力，接触面之间为摩擦接触，摩擦系数取为0.15，并且在管路接头的内部分散着流体压力载荷。

3 结果与讨论

3.1 Gauss粗糙面参数对几何形貌的影响

图9所示为0.25mm×0.25mm区域内，不同粗糙度Ra和自相关长度cl对应的粗糙面高度分布云图，高度值越大的区域颜色越深。对比图9（a）-图9（c），当表面粗糙度相等时，随着自相关长度的增加，不同颜色区域的面积不断升高，这说明自相关长度能够增加粗糙表面的连续性。对比图9（b）与图9（d），当表面的自相关长度相等时，可以看出随着表面粗糙度的增加，表面拥有更大的高度幅值和高度差，这意味着粗糙度较大的表面不平坦。

图8 宏观尺度接触模型及其边界条件 Fig.8 Macroscale contact model and its boundary conditions

图9 不同粗糙度和自相关长度的表面高度分布云图 Fig.9 Surface height distribution cloud images with different roughness and autocorrelation length

3.2 密封性能评价指标的取值

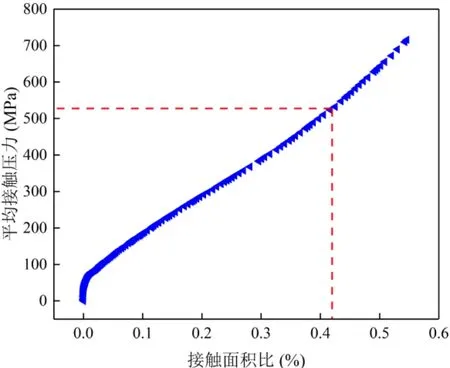
图10 平均接触压力与接触面积比的关系曲线 Fig.10 The relationship between the average contact stress and the contact area ratio

图11所示为两种不同接触面积比对应的密封面接触情况，随着接触面积比α的增大，图中接触区域的面积也随之增大。如图11（a）所示，α=0.3的区域内存在大量未接触的空白区域，这些连通的空白区域会构成泄漏通道，而图11（b）中α=0.41的区域内无明显的泄漏通道。综上可知，由不锈钢材料加工而成的静密封部位，只有当宏观尺度接触区域的接触压力P≥520MPa时才能形成良好的密封效果。

对37°DN6球形管路接头开展气密性试验，将试验件浸入水中，用空气给试验件缓慢加压到45MPa高压，保持5min，试验过程中观察接头连接处是存在气泡，以及气泡的数量。7组试验的结果表明，当预紧扭矩为30～35N·m之间时，管路接头无气泡冒出。参考文献[5]的方法计算得到30N·m扭矩对应的轴向预紧力为9kN左右，该预紧条件下接触面的最大接触压力P=623MPa,大于微尺度临界平均接触压力，利用本文提出的密封性能评价方法得到的结论和试验一致。

3.3 预紧力对密封性能的影响

预紧力F对静密封区域的形成起着决定性的作用。图12为预紧过程中接触长度和接触区域Von Mises等效应力的变化规律。管接头预紧过程中接触长度随预紧力线性增加，这表明预紧力能够增强接头的密封性能。在预紧初始阶段F=0.5kN 时，从接触部位的等效应力云图可以看出，接触部位的最大等效应力σmax=220MPa ，超过材料的屈服极限，这是因为球面和锥面的初始接触类型是点、线接触，接触部位存在应力集中的现象。随着预紧力的增大，接触部位变成线、线接触，高应力区面积不断增加，但高应力区内的球面和锥面将发生不可逆转的塑性变形，塑性变形削弱了管路接头的回弹能力，因此需要找到密封要求对应的最小预紧力，减小预紧力对密封结构的破坏。如图13所示为预紧过程中的接触压力分布情况，随着预紧力的增大，接触压力的幅值和分布长度不断增加，并且高接触压力区主要集中在接触部位，当F=3kN时接触压力P＞520MPa，这意味着能够形成密封区域。

图11 不同接触面积比的密封面接触情况 Fig.11 The contact situation of the sealing surface with different contact area ratio

图12 预紧过程中接触长度和应力面积Fig.12 Contact length and stress area during assembly process

图13 预紧过程中接触压力Fig.13 Contact pressure during assembly process

3.4 介质压力对密封性能的影响

液体火箭发动机的流体介质处于超高压状态，增加了发动机静密封的泄漏风险，分析介质压力pf对管路接头密封部位的影响。在上述预紧力对管路接头密封性能的分析过程中，认为无介质压力情况下预紧力F=3kN即可满足管路接头的密封要求。选取F=3kN,介质压力pf∈ [0,40]MPa 的工况分析介质压力对管路接头密封性能的影响。如图14所示接触部位的长度和应力随介质压力的变化情况，当pf∈ [0,15]MPa 时，接触长度保持不变，高应力区面积减小，高应力区的形状也由无介质压力时的椭圆形变得不规则，两者的最大等效应力都位于靠近流体介质的一侧，并且球面的高应力区面积比锥面的减少更多。当pf∈[20,30]MPa 时接触长度减少3%,高应力区的形状不变但面积进一步减小，此时两接触面发生微小滑移运动。介质压力pf＞30MPa 的接触长度急剧减小，pf=30MPa 对应的接触长度减小16%，这意味着两接触表面发生的显著相对运动。

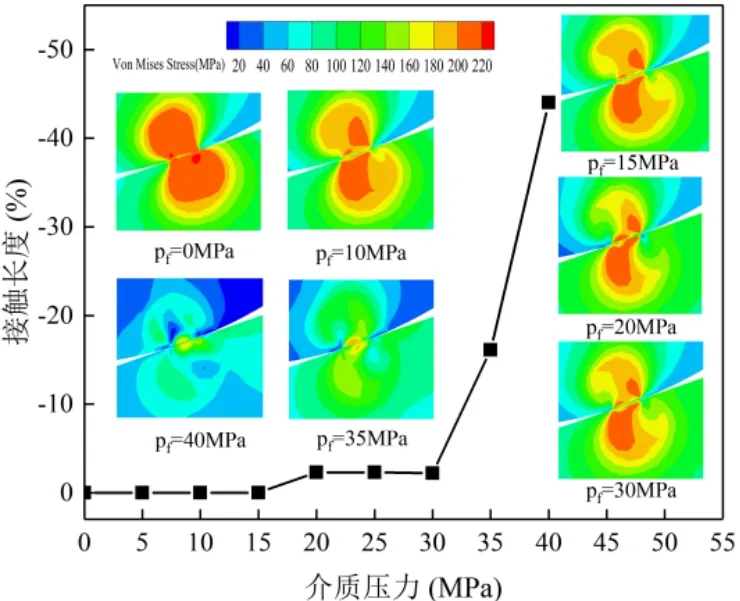
图14 不同介质压力的接触长度和应力面积Fig.14 Contact length and stress area for different media pressures

如图15所示为不同介质压力的接触压力分布变化情况，随着介质压力的升高，密封区域的接触压力幅值和分布范围都呈现下降的趋势，这是因为介质压力抵消了一部分预紧力的作用，导致密封部位的性能降低，管路接头在预紧力F= 3kN的条件下可以承受pf∈[0,10]MPa 的压力，当介质压力过大时只能通过增加预紧力的方式来提高管路接头的密封性能。

图15 不同介质压力的接触压力Fig.15 Contact pressure for different media pressures

3.5 材料搭配的影响

球形接头的材料为不锈钢，接管嘴的材料分别为GH4169、钛合金、不锈钢和铝合金，比较不同材料对管路接头密封性能的影响，如表2所示为相关的材料参数，材料本构均为双线性各向同性硬化。如图16所示为不同材料在预紧力作用下的接触长度变化，当预紧力F＜3kN时，铝合金的接触长度明显高于其它材料的接触长度，这是因为铝合金的弹性模量在所有材料中最小，接触面在挤压的过程中容易发生变形，因此发生接触的区域更多。当F=8kN时，钛合金、不锈钢和铝合金的接触长度相等，相比之下，GH4169的接触长度比其他三种材料少5.7%。保持预紧力F=7kN不变，如图17所示为预紧力相等的条件下，四种材料对应的接触压力分布。屈服极限更大的GH4169和钛合金，它们的接触压力幅值高于屈服极限较低的铝合金与不锈钢，并且接管嘴和球形接头材料相同时的接触压力最低。因此为了提高管路接头的密封性能，推荐使用不同材料搭配的接管嘴和球形接头。

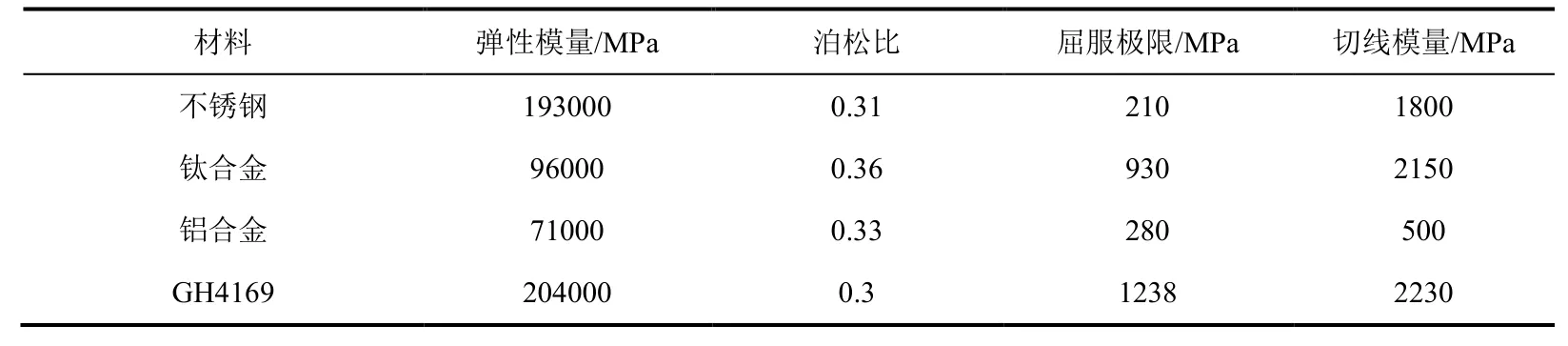
表2 材料参数 Table2 Material parameters

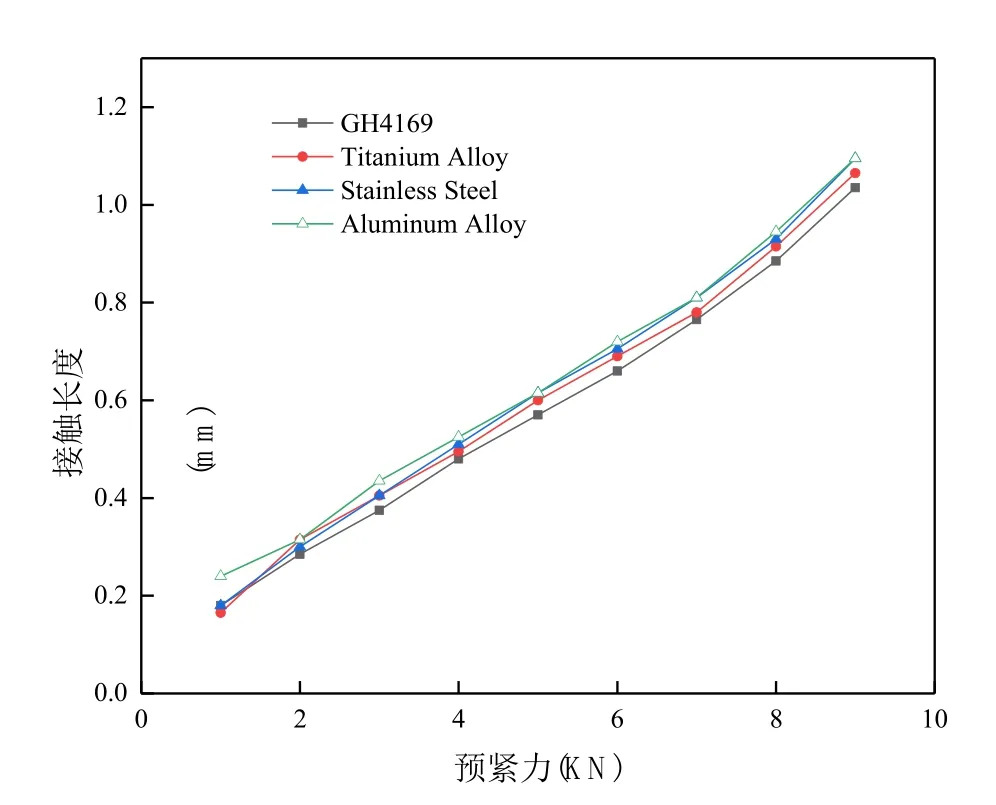
图16 不同材料的接触长度Fig.16 Contact length of different materials

图17 不同材料的接触压力Fig.17 Contact pressure of different materials

4 结论

1）具有Gauss分布特征的随机粗糙表面，随着自相关函数的增加，表面的连续性增强。粗糙度越大的随机表面具有更大的高度差。建立表面粗糙度Ra=1.6um，自相关长度cl=3um的两不锈钢粗糙表面有限元接触模型，得到在临界接触面积αc=0.41对应的临界接触压力=520MPa,并将作为静密封性能的评价标准，应用该指标判断密封性能和45MPa高压气密试验得到的结果相吻合。

2）选取液体火箭发动机DN6不锈钢球形管路接头的密封区域作为研究对象，建立宏观尺度有限元接触模型。在无压力载荷的条件下，随着预紧力的增大，接触部位的高应力区面积不断升高，接触压力的分布范围和接触长度也在增加，当预紧力F=3kN时能够满足密封性能评价标准。介质压力对预紧力起到抵消的作用，并且改变了接触部位的应力分布形状，使接触压力和接触长度下降，预紧力F=3kN的接头可承受[0,10]MPa范围内的介质压力。不同屈服强度的材料搭配可以提高管路接头的密封性能。