斜演化半流一致指数稳定的广义离散型刻画

岳田

（湖北汽车工业学院数理与光电工程学院，湖北十堰 442002）

Lyapunov函数、离散时间方法、Perron型方法、Datko-Pazy 定理等技术工具的运用使微分系统定性理论研究得到了快速发展，尤其是指数稳定性方面得到了学者们的极大关注，取得了丰富的成果［1-12］。值得一提的是，1972年Datko［1］指出具有一致指数有界的演化族U={U(t,s)}t≥s≥0呈现一致指数稳定当且仅当存在p≥1使得

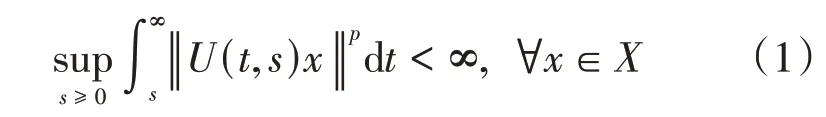
相对于Datko结论选取演化族的第1个分量为积分变量，1967年Barbashin［2］针对演化族第2个分量给出了其一致指数稳定的积分刻画，即演化族一致指数稳定当且仅当

受上述关于演化族一致指数稳定的2 个积分刻画启发，对于线性斜演化半流，Hai在文献［5］中利用Banach函数空间及Banach序列空间分别给出了其一致指数稳定的连续与离散特征，并在文献［7］中给出了其一致指数稳定的连续及离散型Bar‑bashin定理。特别地，Hai在文献［7］中给出了Dat‑ko 与Barbashin 结论的统一离散刻画：线性斜演化半流π=(Φ,σ)一致指数稳定的充要条件为

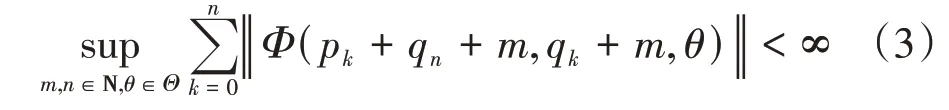
式中：{pk}与{qn}均为非减正序列。

受文献［7］启发，文中给出更为广义的离散型特征来刻画线性斜演化半流的一致指数稳定性，所得结论推广了Datko、Barbashin、Hai等人的结果。

1 预备知识

设X为一Banach空间，(Θ,d)为一度量空间，将空间X上的范数及作用其上的有界线性算子全体ℒ(X)上的范数记作‖ ⋅‖。记I为恒等算子，

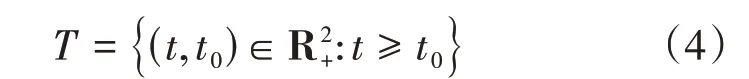
χA为集合A的特征函数，Δα表示所有满足性质

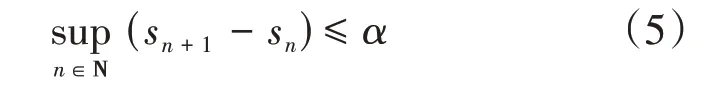
的非减正序列{ }sn构成的集合，[x]表示不超过x的最大整数。

定义1［5］若对任意t≥s≥t0≥0及θ∈Θ满足：

则称连续映射σ:T×Θ→Θ为Θ上的演化半流。

定义2［5］若σ为Θ上的演化半流，且对任意t≥s≥t0≥0及θ∈Θ映射Φ:T×Φ→ℒ(X)满足：

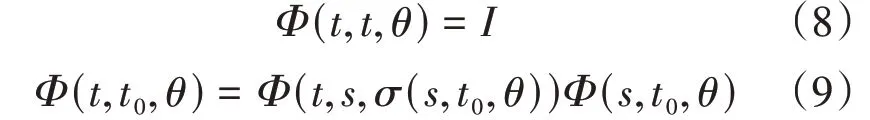
存在常数M≥1与ω> 0使得

称π=(Φ,σ)为ℰ =X×Θ上的线性斜演化半流。

定义3［5］若存在常数N,v> 0使得对任意

则称线性斜演化半流π=(Φ,σ)一致指数稳定。

定义4［6］集合ℱ 表示满足如下条件且定义在正序列上的函数F所构成的全体：

1）当s1≤s2时，

2）存在λ> 0，使得对任意n∈N和α> 0，

3）对任意α> 0，

引理1［6］设F∈ℱ，L> 0。记

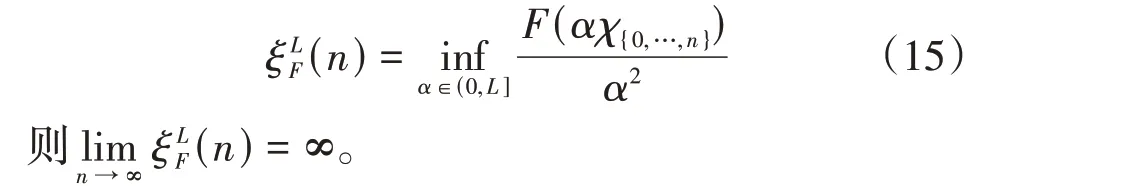
引理2［10］若存在常数l∈N+,n∈N及c∈(0,1)使得对任意不小于n的整数m及θ∈Θ，

则π=(Φ,σ)是一致指数稳定的。

2 主要结论

式（20）中，若j∉{0,…,n}，则

若j∈{0,…,n}，则

证明：1）必要性。若π=(Φ,σ)一致指数稳定，由定义3 知，存在常数N,v> 0 使得式（11）成立。经运算知式（17）～（19）成立，下证式（20）。令

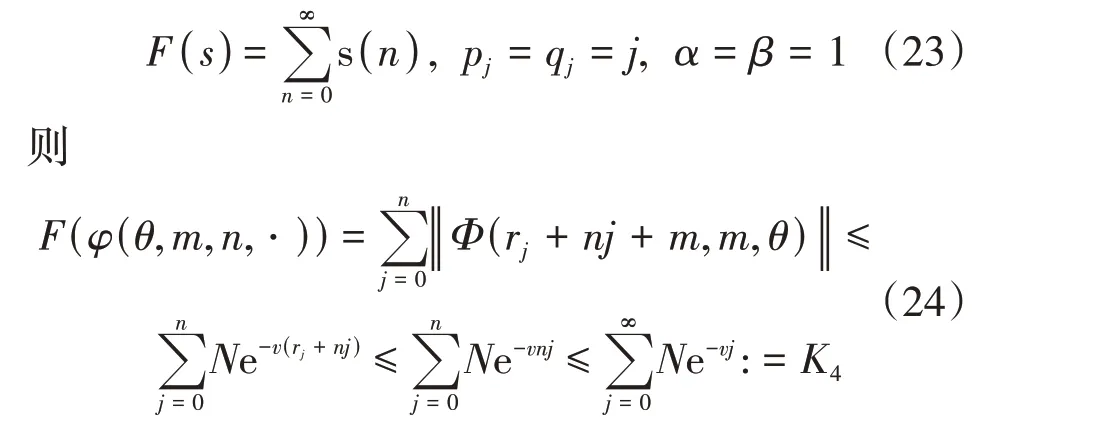
2）充分性。设m,n∈N，j∈{0,1,…,n}。由于

故借助定理1可得π=(Φ,σ)是一致指数稳定的。

3 研究展望

作为公开问题，后续将主要围绕线性斜演化半流的多项式渐近行为开展研究工作，如多项式稳定性、不稳定性与二分性的Datko 型刻画以及Bar‑bashin 型刻画；另一方面，由于随机斜演化半流在随机动力系统的定性理论研究中扮演着重要角色，因此后续将对随机斜演化半流的多项式行为开展进一步研究。