从问题中“来”,到模型中“去”
——关于隐圆模型的解题应用
⦿江苏省常熟市沙家浜中学 曹鸣军
1 引例探究
引例(2021年江苏徐州市中考卷第18题)在△ABC中,若AB=6,∠ACB=45°,则△ABC的面积的最大值为______.
分析:定长AB所对角∠ACB为定角,结合圆周角定理中“同弧或等弧所对的圆周角相等”,可构建圆来体现上述特性,即AB定值→弧AB定长→所对圆周角∠ACB定角,故点C位于过A,B,C三点的圆上.后续利用圆的性质分析最值.
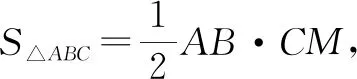

图1

2 模型解读与探究
上述问题突破的关键是求CM的最大值,解析时借助了圆的特殊性质,实则问题中隐含了“定长对定角”隐圆模型.即定长——AB,定角——∠ACB=45°,且二者为相对关系.
2.1 模型解读
若长度固定的线段AB所对的动角∠P为定值,则点P的运动轨迹为过A,B,P三点的圆的一部分,如图2所示.该模型所蕴含的基本原理为弦AB所对同侧的圆周角始终相等.
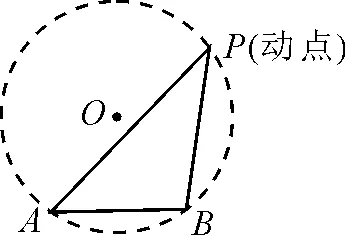
图2
2.2 解题策略
“定长对定角”隐圆模型在几何中有着广泛的应用,实际解题时,建议分三步突破.
第一步,提取“定长”“定角”,确定隐圆模型;
第二步,基于定长和定角所在三角形作外接圆,通过解三角形确定圆心位置及半径;
第三步,利用圆的性质推导关键线段,完成求解.
2.3 问题再探
2021年广东中考卷第17题的破解过程同样涉及到了“定长对定角”隐圆模型,同样利用三点共线来求线段最值.下面进一步探究隐圆模型.
例1(2021年广东中考卷第17题)在△ABC中,∠ABC=90°,AB=2,BC=3.点D是平面上的一个动点,∠ADB=45°,则线段CD长度的最小值为______.
分析:已知AB=2,∠ADB=45°,显然满足“定长+定角”,可构建隐圆⊙O,则点D在⊙O上运动.结合几何性质可确定⊙O的半径,利用圆的性质、三点共线可确定最值情形.


图3

3 拓展探究
隐圆模型可有效用于几何问题求解,如最值问题、取值问题、求线段长问题等.隐圆模型的类型较为众多,除了上述的“定长对定角”模型外,还有常用的“直径对直角”模型、“四点共圆”模型等.下面结合实例进一步探究隐圆模型.
拓展模型一:“直径对直角”模型
“直径对直角”模型,即点C是线段AB外的一点,若∠ACB=90°,则点C位于以AB为直角的圆上;也可逆向推导,若点C位于以AB为直径的圆上,则∠ACB=90°.该模型是基于圆周角定理所构建的.解题时可依据该模型来确定动点轨迹,也可推导夹角大小.
例2(2021年江苏常州市中考卷第18题)如图4所示,在Rt△ABC中,∠ACB=90°,∠CBA=30°,AC=1,D是AB上一点(点D与点A不重合).若在Rt△ABC的直角边上存在4个不同的点分别和点A,D成为直角三角形的三个顶点,则AD长的取值范围是______.

图4
分析:要求Rt△ABC的直角边上存在点与A和D组成直角三角形,则可以借助“直径对直角”模型,以AD为直径画圆,与BC和AC的交点就为其中满足条件的点.后续利用圆的性质即可推导AD的取值范围.
解:以AD为直径作⊙O,与BC的相切于点M,连接OM,则OM⊥BC,此时在Rt△ABC的直角边长存在3个不同的点分别和点A,D组成直角三角形,如图5所示.逐步增大AD长,则⊙O与BC将有两个交点,可出现满足条件的4个点.当AD=AB时,则只有1个满足条件的点.

图5
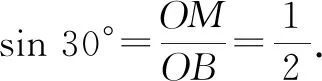
当点D与点B重合时,即AD=AB=2,即AD的最大极限为2.

评析:上述探究的核心是构建直角三角形,故可引入“直径对直角”隐圆模型来研究线段长问题.同时解析过程涉及到了动态分析,可通过研究极限情形来“化动为静”.
拓展模型二:“四点共圆”模型
“四点共圆”模型,即在同一平面内的四个不同的点在一定条件下可以确定一个圆,利用该模型的性质可以推导角度关系,以及线段长.而构建“四点共圆”模型的策略有多种,可以从线段长入手,也可借助四边形的性质.
例3(2021年浙江嘉兴市中考卷第9题)如图6,在△ABC中,∠BAC=90°,AB=AC=5,D在AC上,且AD=2,点E是AB上的动点,连接DE.点F,G分别是BC和DE的中点,连接AG,FG.当AG=FG时,线段DE的长为( ).
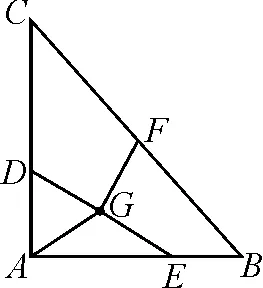
图6
分析:E是AB上的动点,在Rt△ADE中,始终有AG=DG=GE,所以当AG=FG时,点A,E,F,D到点G的距离相等,即四点共圆,且点G为圆心.结合圆周角定理可推知△DEF为直角三角形,由勾股定理,可求解.


图7

评析:上述解析过程充分结合中点特性推导线段等长关系,推知四点共圆,构建了隐圆模型,进而提取直角三角形,隐圆模型在解题过程中起到了关键作用.实际上,证明全等三角形可推知△DEF为等腰直角三角形,进而求出直角边DF长也可完成求解.
4 教学反思
上述通过剖析考题解法,提取其中的几何模型,并深入探究了隐圆的几个重要模型,其中隐圆的构建策略及模型特征有着重要的学习价值,下面结合教学实践,进一步反思.
4.1 关注几何圆,总结圆的特性
圆是初中几何较为特殊的图形,其弧状特征区别于其他图形,理解圆的定义,掌握圆的几何性质是探究学习的关键.尤其是垂径定理、圆周角定理、圆心角定理,是后续构建隐圆模型的关键.教学中要引导学生深入总结圆的特性,结合几何知识开展定理证明.同时可对定理进行归纳,深入剖析定理中角度、弦长之间的关系,构建几何联系.
4.2 注重问题引导,体验探究过程
上述隐圆的探究过程,采用了问题引导、知识探究的方式,即从典型中考题入手,引导学生解析问题,然后开展解后反思,总结提炼模型.这种探究方式可以极大地调动学生的思维,让学生参与教学过程,从问题中“来”,回归到问题中“去”,深刻感知模型的应用价值.因此,实际教学应多采用问题引导、过程探究的方式,引导学生反思、归纳,生成相应的解题策略.
4.3 重视构图过程,掌握建模方法
隐圆构建是解题的关键,从上述解析过程可知,隐圆的构建是建立在对应的知识基础上,如原考题结合“同弧或等弧所对的圆周角相等”来构建圆,例2结合“圆上各点到圆心的距离相等”来构建圆.因此构图背后所隐含的是圆的性质定理及作图方法,故教学中要引导学生总结隐圆的构建策略,包括从角度入手、等线段长入手等,帮助学生总结建模方法,提升建模能力.
总之,深入探究典型问题的解析方法,挖掘问题中隐含的模型价值,对于提升解题能力有着极大的帮助.隐圆模型在几何问题中有着广泛的应用,同时隐圆具有多种模型,上述所探究的只是其中较为常用的三种,除此之外还有“定点定长”模型、“定角定高”模型等.教学中要引导学生勤思考、多总结、巧运用,合理渗透模型思想,充分提高学生的数学思维能力.

