全尾砂-废石膏体流变特性及阻力演化

尹升华，闫泽鹏✉，严荣富，李德贤，赵国亮，张鹏强

1) 北京科技大学土木与资源学院，北京 100083 2) 北京科技大学金属矿山高效开采与安全教育部重点实验室，北京 100083 3) 金川集团股份有限公司镍钴资源综合利用国家重点实验室，金昌 737100

全尾砂-废石膏体充填是矿山发展的核心方向[1-2].它能够有效地降低矿山固体废物的排放，有利于矿床安全清洁高效开采的实现，也能够降低充填采矿的生产成本，促进矿山绿色开采与矿山经济的协调发展[3-6].膏体通常是在充填站进行制备，然后通过管道系统输送到地下采空区[7-8].为了保证矿山生产效率与管道输送稳定性，膏体通常应满足一定的流动性要求，常见的流动性评价指标为流变特性参数[9]（屈服应力和塑性黏度）.目前，国内外专家学者针对膏体的流变特性进行了大量的实验研究.如，蔡嗣经等[10]引入Papanastasiou 模型对充填料浆的黏度和切应力变化过程进行表征，并证明该模型对于流体性质预测的可行性.Boylu[11]等研究了颗粒的粒度分布对水煤浆流变学的影响.Petit[12]等对两种不同种类砂浆的屈服应力值随时间和温度变化的耦合影响进行了评估.可以看出，前述研究的对象均为细粒级浆体，所得结果并不适用于全尾砂-废石膏体.

阻力特性也是评价膏体管道输送可行性的重要依据[13].传统的膏体管道输送阻力的研究一般分为2 种方式.一种方法是阻力损失经验公式，如金川公式、鞍山矿院公式[14]等.但是，其仅适用于特定条件下的充填输送，不具有广泛性.另一种方法是相似实验，采用小管径装置进行实验，然后将计算结果折算到大管径管道中[15].虽然这种方法为管道输送的研究提供了思路，但是由于现场条件的多变性，导致结果与实际输送情况相差较大.近年来，计算流体力学（CFD）模拟成为研究膏体阻力特性的一种有效的方法[16].如杨天雨等[17]应用Fluent 软件按照矿山的实际充填管路进行等比建模，研究了不同影响因素对阻力损失的影响规律.张钦礼等[18]建立了长距离的二维管道模型，发现料浆自流输送需要满足重力产生的压力值大于阻力损失值.吴迪等[19]采用模拟手段分析了某矿充填管道输送过程中弯管的受力情况，为充填系统的顺利运行提供了理论支撑.王新民等[20]基于FLOW-3D 综合多种影响因素研究发现西部某膏体充填站的最佳输送倍线为3.0.然而，还没有一种可以有效预测全尾砂-废石膏体流动特征的模型.

本实验的主要目的是考察全尾砂-废石膏体的流变特性及阻力演化行为.研究了粗骨料膏体的流变参数变化特性，构建了考虑体积分数、堆积密度及灰砂比的输送阻力数值模型.并基于Comsol 软件分析了不同尾废比、入口速度、及浓度对输送阻力的影响规律.本文的研究成果对于粗骨料膏体输送技术的发展及减小管输阻力、延长输送距离具有积极意义.

1 实验材料

本实验所用实验材料均取自金川公司二矿区，全尾砂和废石的物理化学性质如下：

（1）全尾砂取自二矿区选厂，晾晒并烘干后测其密度为2.785 g·cm-3，松散堆积密度和堆积密度分别为1.21 g·cm-3和1.527 g·cm-3.采 用LMS-30型激光粒度分析仪测试全尾砂的粒度组成，粒度分布见图1（a）.可以看出，粒度小于80 μm 的尾矿占91.31%.尾矿砂的主要化学成分采用X 射线荧光（XRF）光谱分析，结果见表1.全尾砂的活性根据国家标准GB/T20491—2006、GB203—2008、GB/T18046—2008 采用用碱度、活度、质量指数等指标进行评价，如表2 所示.表2 数据标明二矿区全尾砂是一种低活性的填充材料.

表1 充填材料化学成分Table 1 Chemical composition of the filling material

（2）废石取自二矿区充填站料仓.测其密度为2.876 g·cm-3.松散堆积密度和致密堆积密度分别为1.675 g·cm-3和1.968 g·cm-3.用筛分法测试废石的粒度分布，粒度曲线如图1（b）所示，可见0～12 mm的废石占87%，小于15 mm 的废石占99.9%，废石骨料粗颗粒含量较多，会对管道输送产生不利影响.废石的活性指标在表2 中给出，可以看出废石同样为低活性的充填材料.

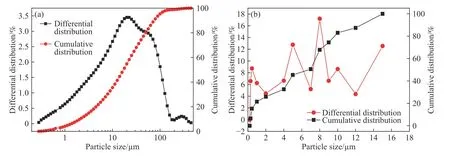
图1 粒度分析结果.(a)全尾砂;(b)废石Fig.1 Particle size analysis results: (a) unclassified tailing;(b) waste rock

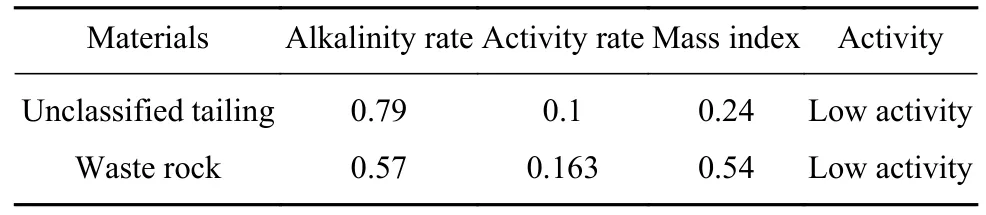
表2 充填材料活性指标Table 2 Activity index of the filling material

（3）堆积密实度是表征粗骨料混合性能的一个重要指标，其主要反映的是细骨料填隙效应的优劣.经实验得到的不同全尾砂-废石配比的密实度如表3 所示.预实验中发现全尾砂-废石质量比（尾废比）达到3∶7 后料浆稳定性降低，会严重影响料浆的阻力特性.因此，本文选取中间三组连续的配比（尾废比4∶6、5∶5 和6∶4）进行实验.

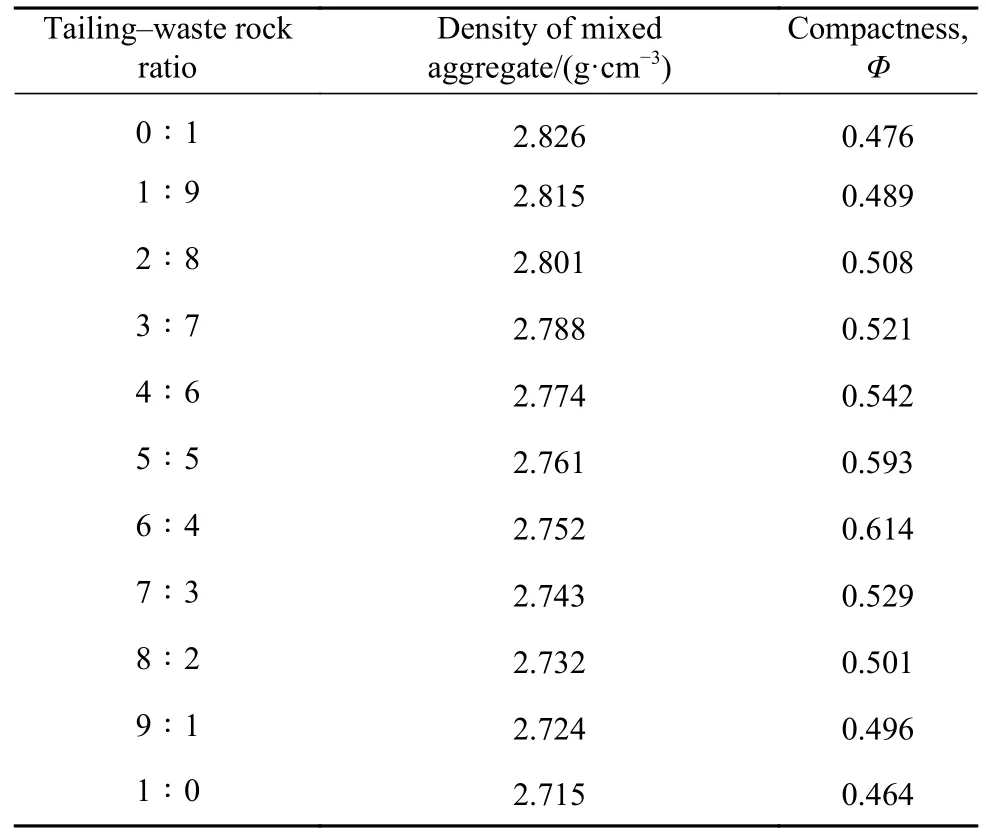
表3 混合骨料的堆积密实度Table 3 Stacking compactness of the mixed aggregate

2 全尾砂-废石膏体的流变特性

2.1 流变测试

采用Brookfield R/S+型流变仪对全尾砂-废石膏体的流变特性进行测试.该流变仪配备规格为v40-20 的桨式转子，即桨叶直径为20 mm，高度为40 mm.为了避免干尾砂颗粒与水之间不充分混合所造成的测量误差，使用搅拌机以200 r·min-1的转速搅拌2 min 后再进行流变测试.采用控制剪切速率法对废石膏体的流变特性进行测试（流变实验方案如表4 所示）.流变测试共包括两部分内容：1）固体质量分数（选择67%～77%质量分数进行测试）对流变特性的影响；2）尾砂和废石的质量比，即尾废比，选择4∶6/5∶5/6∶4 3 组进行测试.流变测试流程如下：首先使转子保持恒定剪切速率（220 s-1）对膏体进行2 min 的恒定剪切；待膏体达到应力松弛阶段后，设置剪切速率以0.1 s-1逐渐递减，在变剪切速率下测试膏体的流变特性，该阶段持续时间共220 s，流变测试剪切过程如图2 所示.最终得到全尾砂-废石膏体的流变特性曲线，如图3 所示.

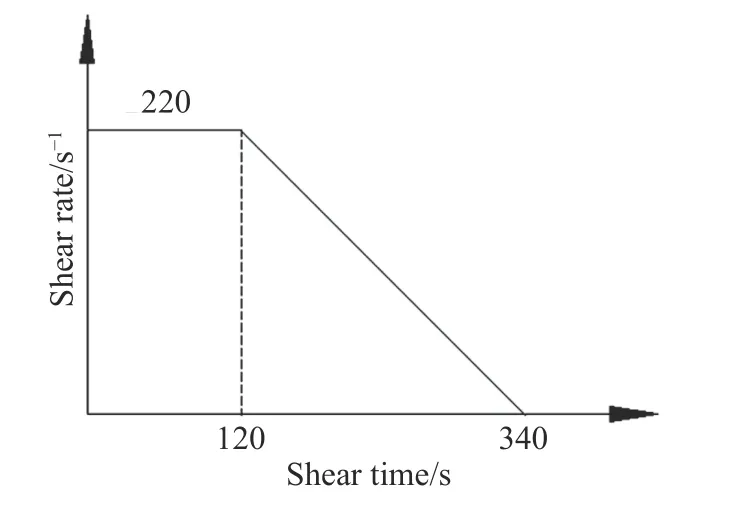
图2 流变剪切过程示意图Fig.2 Schematic of the rheological shearing process

表4 流变测试方案Table 4 Rheological test summary

图3 为不同固体质量分数条件下膏体的流变特性曲线.可以看出，流变曲线的“第二阶段”基本呈线性增加，其规律符合“宾汉姆塑性体”的特征[21].因此，使用宾汉姆公式，如式（1）拟合流变结果，得到不同工况下膏体的流变参数值.拟合结果见表5.

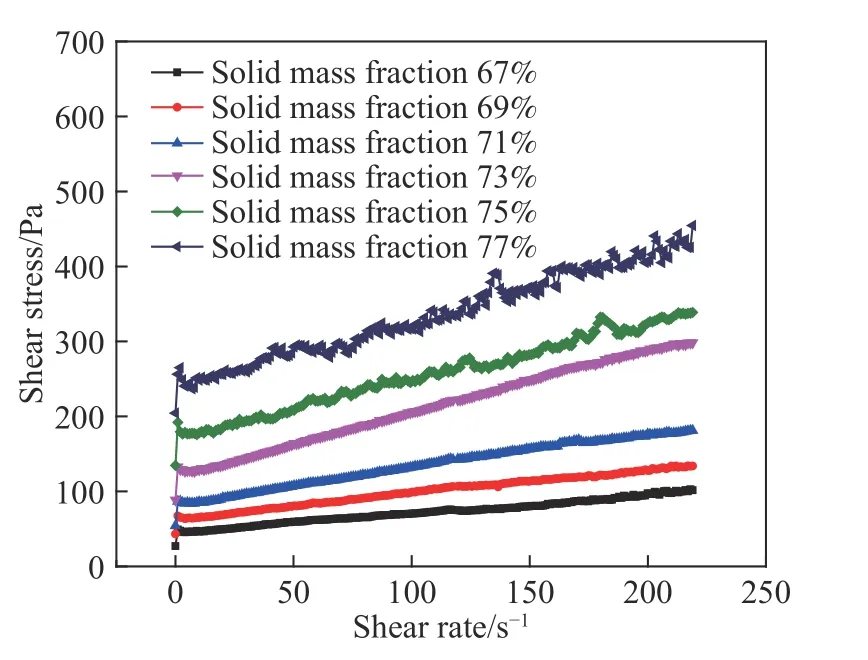
图3 流变特性曲线（尾废比6∶4）Fig.3 Rheological characteristic curve (tailing-waste ratio is 6∶4)

式中：τ为料浆的实时剪切应力，Pa；τ0为料浆的屈服应力，Pa；η为料浆的塑性黏度，Pa·s-1.

2.2 拟合结果分析

根据表5 中数据做固体质量分数和尾废比对流变参数影响的曲线图，如图4～5 所示.图4 表明，随着料浆中固体含量的增加，充填物料的屈服应力在不断地增大，且增长的幅度越来越大，而塑性黏度也呈增长的趋势但是增长幅度在逐渐减小.分析认为，固体质量分数变大时会促进尾砂颗粒间的“絮网”结构[22]的形成过程，“絮网”结构会对转子的转动产生较大的阻力，所以随着固体质量分数的增大料浆的屈服应力随之增大.而粗骨料膏体孔隙较多且具有一定“保水性”，当受到剪切作用时“被包裹”的水被释放，导致塑性黏度的增长率降低.图5 表明，随着尾砂所占比例的增加粗骨料膏体的屈服应力及塑性黏度均呈增长的趋势.这主要是由于尾砂颗粒粒径小于废石，其可以填充在废石颗粒之间形成一种相对稳定的骨架结构.随着尾砂含量的增加这种结构越来越稳定，进而促进了屈服应力和塑性黏度的增长.

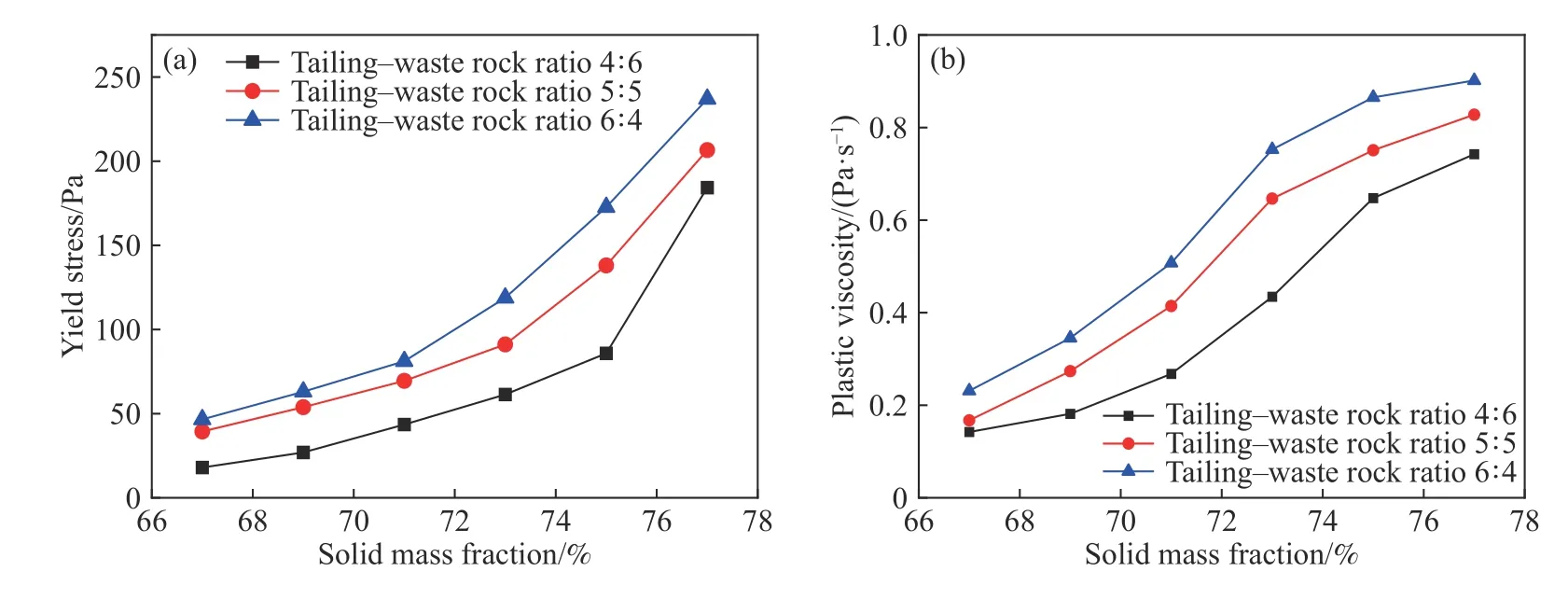
图4 固体质量分数对流变特性的影响Fig.4 Effect of the solid mass fraction on the rheological properties

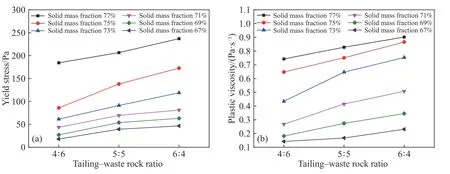
图5 全尾砂-废石比对流变特性的影响Fig.5 Effect of the tailing-waste rock ratio on the rheological properties

表5 流变参数拟合结果Table 5 Fitting results of rheological parameters

2.3 全尾砂-废石膏体阻力模型

2.3.1 流变参数方程

屈服应力与料浆中水的含量、水泥量、骨料的级配都存在着密切的关系[23].研究表明，屈服应力与骨料体积分数，以及水泥与骨料的质量比（灰砂比）之间存在定性的关系.对全尾砂-废石膏体的屈服应力进行“屈服应力-体积分数”和“屈服应力-灰砂比”的拟合，拟合结果如表6 所示.可以看出，废石膏体的料浆屈服应力与体积分数、屈服应力与灰砂比呈负幂指数关系.

表6 屈服应力拟合结果Table 6 Yield stress fitting result

由表3～4 数据可以看出，体积分数的增加（固体质量分数的增加）和灰砂比的减少（固体质量分数的增加）均会导致屈服应力的增加，所以灰砂比与骨料体积对屈服应力的影响是同步的.同时，屈服应力与料浆的配比也存在着紧密的关系，为了使方程达到最简，并且能够清晰的表达出影响因素与屈服应力的关系，提出了如下屈服应力预测模型：

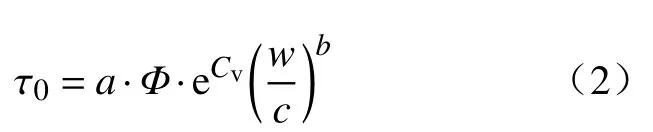
式中：w/c为灰砂比；Φ为骨料堆集密实度；Cv为体积分数；a为常数，Pa；b为实验常数.

膏体料浆中絮网结构的固体物质比重以及细粒级含量是导致黏度变化的根本原因，这为黏度计算模型的构建提供了思路.通过对塑性黏度影响因素的分析，发现影响塑性黏度的主要因素为膏体浓度和膏体稳定系数，黏度特性虽然受级配特征的影响，但细颗粒含量参数不能直接描述塑性黏度增长特征.

塑性黏度随膏体料浆浓度基本呈幂函数形式增长，同时在体积分数一定的情况下，堆积密实度的减小意味着提高了料浆的有效浓度，进一步促使黏度的增长.为表现不同因素与塑性黏度的关系，同时实现塑性黏度的简明预测，提出了全尾砂膏体塑性黏度预测模型：

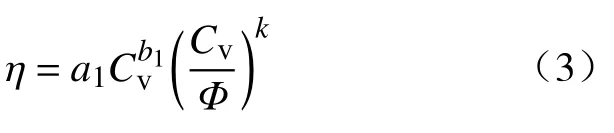
式中：η为塑性黏度，Pa·s-1；a1，b1，k为实验常数.在origin 中采用式（2）和式（3）对实验数据进行拟合得到不同尾废比条件下公式中未知常数的确定值.如表7 所示.结果显示相关系数R2均在0.95以上，说明流变参数模型的自适应性良好.

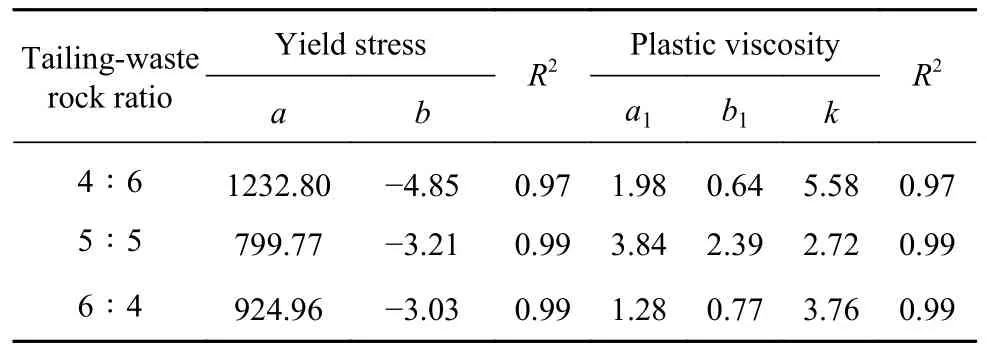
表7 参数拟合结果Table 7 Parameter fitting result

2.3.2 全尾砂-废石膏体阻力计算方程

膏体的输送阻力通常通过典型的宾汉流体阻力方程进行计算[24]，如式（4）所示.在管径和流速已知的情况下采用该方程进行阻力计算时，管道阻力主要受到屈服应力和塑性黏度的制约.将前述得到的屈服应力和塑性黏度公式带入到式（4）就得到了考虑物料综合配比的输送阻力i计算公式，如式（5）所示.

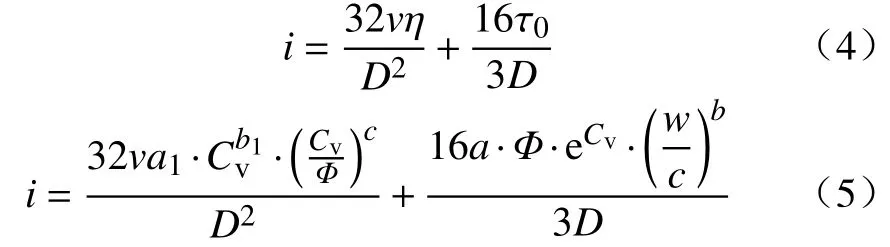
式中：v为料浆的平均流速，m·s-1；D为管道直径，mm.

式（5）通过对传统的宾汉流体阻力方程中的流变参数进行替换，将体积分数、密实度和灰砂比代入到阻力方程中，可从多个角度综合骨料配比对输送阻力的影响.观察可知，在流速条件确定时，料浆自身的配比参数是影响阻力损失的关键因素，该公式的提出对于粗骨料膏体输送理论的进一步发展具有积极的意义.

3 数值模型建立

COMSOL 是一款应用于模拟仿真的有限元软件，它与传统的有限元模拟软件的复杂操作不同，我们进行多物理场耦合分析时仅需要相应选择所需的微分方程就可实现，非常方便快捷，该软件在声学、流体动力学、多孔介质等多个方向得到广泛的关注.

3.1 模型基本控制方程

COMSOL 内嵌描述流体的流动方程为纳维-斯托克（N-S）方程[25]，其基本表达式为：

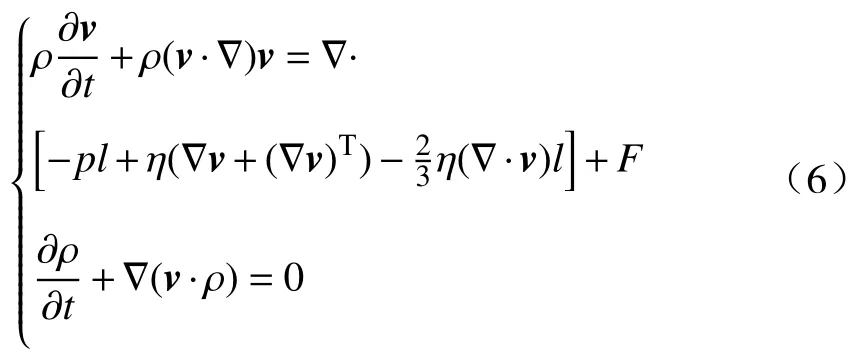
式中：ρ为流体密度，kg·m-3；v为料浆流速向量；p为流体压力，Pa；t为流体流动时间，s；F为所有作用在流体上的外力（体积力），Pa；l代表流体运动的距离，m；∇为梯度算符.通过修改式中的体积力F，将上文推导的阻力计算公式带入到N-S 方程中对方程的弱解形式进行离散，建立综合考虑体积分数、堆积密度及灰砂比的数值模型.

3.2 几何模型构建及参数设置

模拟实验根据金川二矿地表充填钻孔至-1350 m水平的充填管路系统（现用充填管径150 mm）进行几何模型的构建.根据雷诺数相似理论，将其简化为一个长10 m、高2.5 m 的“L 型”模型，如图6 所示.模型设置入口为“速度入口”.由于添加重力为体积力，设置管道出口边界条件为0 或层流流出会导致模拟计算不收敛，需要设置出口为开放边界且无黏滞应力并加入压力积分为0 的约束.

COMSOL 软件自带的网格剖分工具有很强的编辑能力，用户可根据自己的需求调整网格的形状、大小等.选择细化自由三角形网格对几何进行划分，设置模型的边界层数为6、边界拉伸系数为1.2，以使网格更密集，最终单元数目为228700，网格细节如图6 所示.

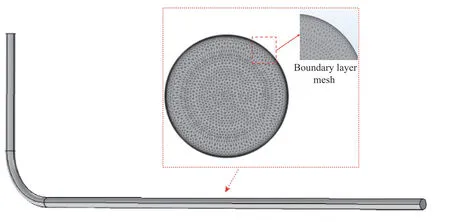
图6 管道几何结构及截面网格剖分图Fig.6 Diagram of the pipeline geometry and section meshing

3.3 数值模拟方案

本次数值模拟考虑影响因素共有3 个，分别为：尾砂与废石的质量比4∶6、5∶5 和6∶4；固体质量分数73%、75%和77%；模型初始流速2.0、2.2 和2.4 m·s-1.通过Comsol 后处理提取不同尾废比、固体质量分数及初始流速条件下的压降演化规律进行分析.充填物料的流动形态通过雷诺数进行确定，其中Re＜2300 属于层流、Re＞4000 属于紊流.雷诺数计算公式如下：

式中：U为特征速度，m·s-1.根据前述设置条件计算得到尾砂-废石膏体的雷诺数均小于2300，认为其在管道输送过程中处于层流状态.

4 全尾砂-废石膏体输送阻力演化特征

4.1 模拟验证

为了评估本文建立数值模型的可靠性与适用性，采用金川二矿所得充填物料进行了充填环管试验，通过在模拟环路上安装压力变送器对膏体阻力损失进行测量.环管参数为：管径150 mm；固体质量分数73%～77%；尾废比4∶6；流量120 m3·h-1（换算后流速约为1.9 m·s-1），压力监测管路长度17.13 m.根据环管实验参数，在Comsol 中建立一个长为17.13 m、管径150 mm 的水平直管模型，其中网格剖分和边界条件的设置（速度入口固定为1.9 m·s-1）均和上文相同.环管实测数据与数值模拟数据如图7 所示.

由图7 可以看出，在不同固体质量分数的情况下环管实测数据和数值模拟数据的相对误差在8%以内，模型的自适应性良好说明前述构建的数值模型用于全尾砂-废石膏体管输阻力的计算是可靠的.

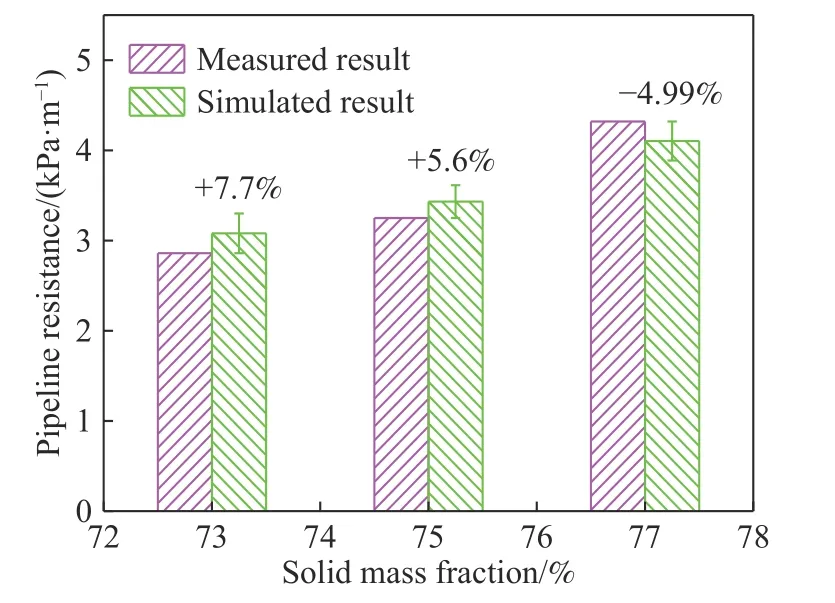
图7 模型验证Fig.7 Model validation

4.2 全尾砂-废石膏体阻力演化特征分析

4.2.1 尾废比对阻力损失的影响

骨料粒度组成的差异对充填料浆的输送行为具有重要的影响，为了降低矿山生产成本同时在充填过程中进行多固废的协同利用，进行了不同配比条件下全尾砂-废石膏体的管道输送阻力损失模拟，结果如图8 所示.

图8 表明，随着尾废比的增加阻力损失呈先减小后增大的趋势，不同条件下的阻力损失均在尾废比5∶5 时达到最小值，说明此尾废比条件有利于实际应用.分析认为此现象的产生可归因于膏体物料颗粒级配的影响，当尾废比为4∶6，膏体中粗颗粒（废石）的含量较多，此条件下膏体的稳定性较差，从而导致阻力损失的增大；而尾废比为6∶4 时，物料中的细颗粒成分较多，浆体密实度最高，表明骨料结构较致密.此时，浆体的黏性较强这使得颗粒与管壁的摩擦增强，从而导致较大的阻力损.可以看出，尾废比为5∶5 时膏体物料具有较稳定的结构，同时输送阻力最低，更有利于管道输送.配合比是影响粗骨料膏体输送的一个关键条件，其在物料制备过程中相对容易去进行控制，基于本实验结果建议全尾砂-废石的最佳配比为5∶5.

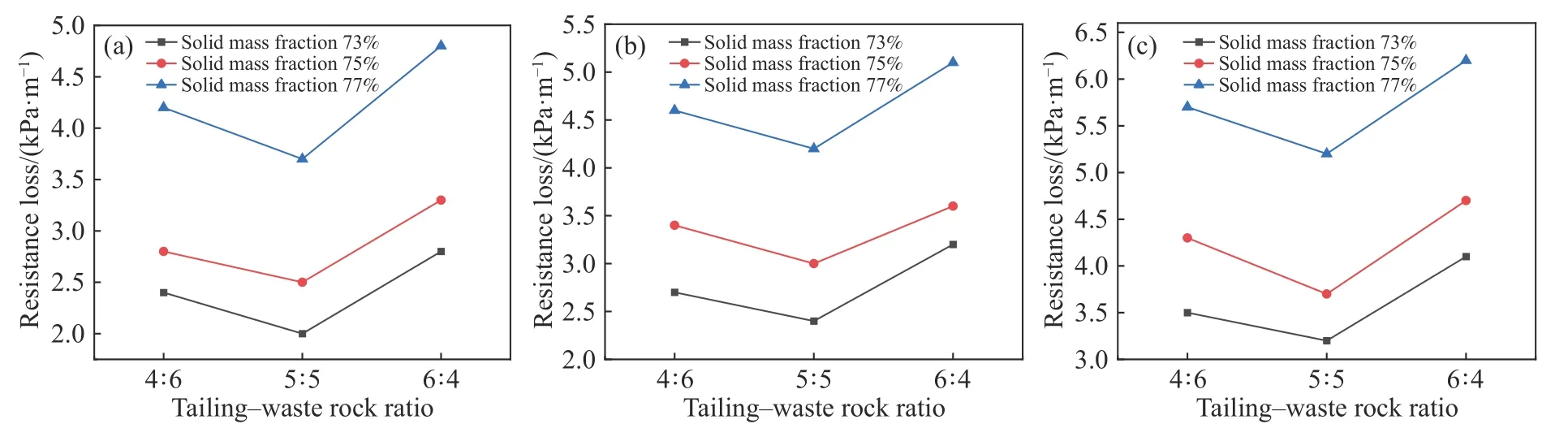
图8 不同初始速度下尾废比对阻力损失的影响.(a) 2.0 m·s-1;(b) 2.2 m·s-1;(c) 2.4 m·s-1Fig.8 Effect of the tailing-waste rock ratio on the drag loss with different initial velocities: (a)2.0 m·s-1;(b) 2.2 m·s-1;(c) 2.4 m·s-1

4.2.2 固体含量对阻力损失的影响

由全尾砂、水泥和废石组成的固相含量是影响浆体管道输送性能的重要因素.固体质量分数过高会导致堵管、爆管现象导致充填料不能够顺利的输送至地下采场.图9 显示了不同固体质量分数条件下的膏体输送阻力损失的变化情况.

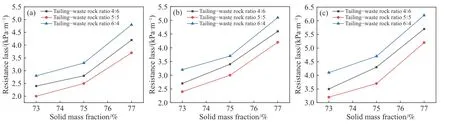
图9 不同初始速度下固体质量分数对阻力损失的影响.(a) 2.0 m·s-1;(b) 2.2 m·s-1;(c) 2.4 m·s-1Fig.9 Effect of the solid mass fraction on the drag loss with different initial velocities: (a) 2.0 m·s-1;(b) 2.2 m·s-1;(c) 2.4 m·s-1

与预期的一样，粗骨料膏体的阻力损失随着固体质量分数的增加而增大且增长速率在逐渐提升.此行为产生的主因是由于固体含量的增加导致浆体水分含量减少所引起的.当粗骨料膏体流经管道时，水起到润滑剂的作用.因此，水含量的降低（固体质量分数增大）使粗骨料浆体难以流动，从而提高了膏体输送的阻力损失.在矿山实际充填过程中，粗骨料膏体应选择适当的固体含量，以达到良好的输送性能.此外，膏体的阻力损失还应该满足矿山实际的充填情况（如浆液搅拌机的处理能力、泵的输送能力等），在保证料浆流动性和可输送性的同时应当最大限度的去提高膏体的浓度，以确保能够最大限度的去提高矿山充填开采能力及固废消耗能力.

4.2.3 初始流速对阻力损失的影响

料浆的初始流速的不同会影响膏体输送的稳定性，进而影响管道阻力损失.初始流速对浆体的影响主要体现在促进颗粒碰撞及摩擦等方面.为了确定全尾砂-废石膏体最佳的输送速度，采用模拟手段进行了2.0～2.4 m·s-1条件下的阻力损失模拟，模拟结果如图10 所示.

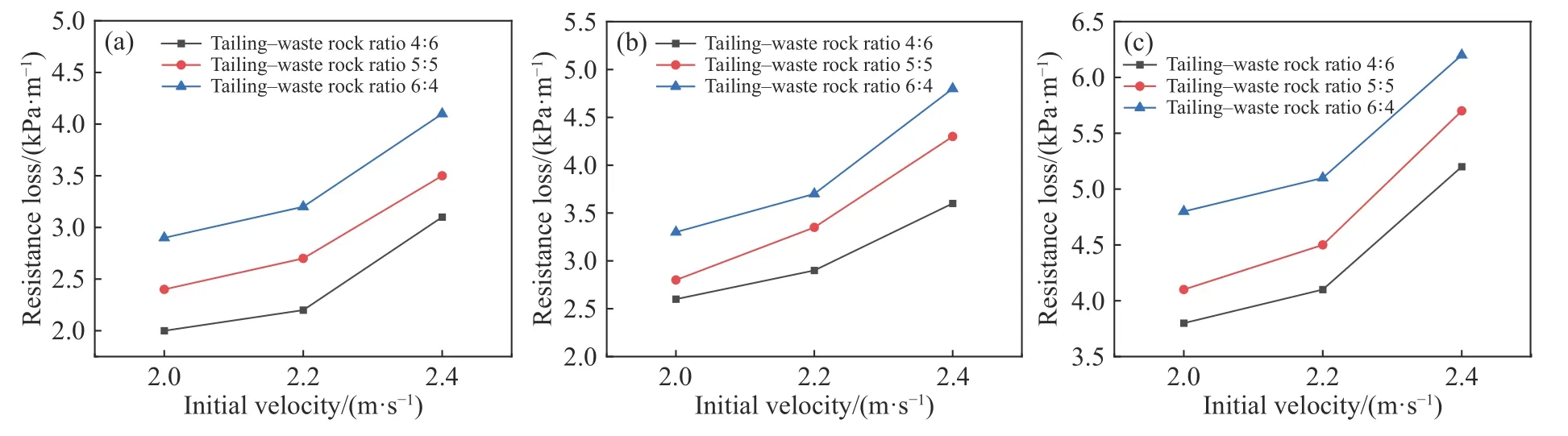
图10 不同固体质量分数下初始速度对阻力损失的影响.(a) 73%;(b) 75%;(c) 77%Fig.10 Effect of the initial velocity on the resistance loss with different solid mass fractions: (a) 73%;(b) 75%;(c) 77%

通过图10 可以看出，随着初始流速的增大，阻力损失呈增大的趋势，且增长速率提高.以固体质量分数77%、尾废比5∶5 条件下的阻力损失为例，当初始速度由2.0 增大至2.2 m·s-1，阻力损失增长0.39 kPa·m-1，增长率为10.2%；由2.2 增大至2.4 m·s-1时，阻力损失增长1.05 kPa·m-1，增长率为24.94%，初始速度2.2 m·s-1处为阻力损失的“拐点”.分析认为粗骨料膏体内部颗粒在输送过程中，会产生一定的紊动能量，形成紊动强度[26].物料颗粒所受紊动作用力公式如下：

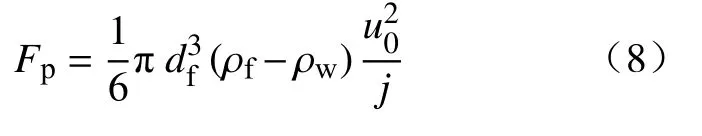
式中：Fp为颗粒在紊动水体中所受的力，N；df为尾砂颗粒粒径，mm；ρf和ρw分别为尾砂颗粒和水的密度，kg·m-3；u0为管内平均输送速度，m·s-1；j为尾砂颗粒的移动距离，mm.由式（8）可以看出，当初始速度增大时导致管内尾砂颗粒所承受的紊动作用力发生变化，从而提高颗粒的碰撞几率与摩擦效应，这使得膏体物料管输过程中的能量利用率降低，相应的阻力损失增大.同时，由于流体的“分层效应”[27]，不同流层间的剪切作用随着初始流速的增加而增大，导致阻力损失的增长率出现随流速的增加而增大的现象.适当的初始流速（流量）是保证矿山生产效率的重要因素，但是流速过大时会导致阻力损失的过度增长.因此，结合数值模拟结果建议全尾砂-废石膏体的最佳初始速度应控制在2.2 m·s-1.

5 结论

(1) 对全尾砂-废石膏体的流变特性进行了测试，并回归得到流变参数的变化规律.塑性黏度和屈服应力随着粗骨料膏体固体质量分数和尾废比的增加均呈增大的趋势.

(2) 建立了综合考虑膏体物料密实度、体积分数及灰砂比的输送阻力数值模型.将数值模拟结果与环管实测结果进行对比，相对误差均在7%以内，证明该模型对粗骨料膏体的输送阻力进行计算是可靠的.

(3) 通过模拟手段得到尾废比、固体质量分数、初始流速对阻力损失的影响规律.颗粒间的摩擦效应导致阻力损失随尾废比的增加呈先增大后减小的趋势；固体质量分数增大导致浆体流动性变差，阻力损失快速增长；初始流速增加，颗粒运动变得不稳定，摩擦加剧，阻力损失增加.

(4) 根据模拟结果得到本实验条件下粗骨料膏体管道输送的最佳参数分别为：尾废比5∶5、初始流速2.2 m·s-1.该结论对粗骨料膏体的管输设计具有一定的指导意义.