颗粒粒径对尾砂膏体触变性的影响

张连富，王洪江，吴爱祥，杨 科

1) 安徽理工大学矿业工程学院，淮南 232001 2) 北京科技大学土木与资源工程学院，北京 100083

高浓度料浆充填和堆存技术是尾砂绿色无害化处理的重要手段[1]，该技术将尾砂掺加水和胶结剂后制成高浓度料浆即膏体，再将其输送到井下采场或堆存在地表.尾砂膏体固体体积分数高，是典型的非牛顿流体，具有屈服应力，在膏体制备、管道输送和堆存过程中还会表现显著的触变性[2].触变性被定义为：充分静置的料浆流动时黏度随时间不断减小，流动终止后黏度随即恢复的现象[3-4].有效预测尾砂膏体的流变行为是调控膏体流动行为的前提，复杂工况下的流变预测更是流变学者们关心的问题[5]，阐明尾砂膏体的触变性是全面理解其流变性的重要补充.

影响料浆触变性的因素有温度[4]、剪切作用[3]、灰砂比和浓度[6]等.颗粒粒径是影响膏体料浆流动行为的重要因素[7]，其对料浆流变性的影响得到了很多关注[8]，但与触变性的关联尚未见报道.不同的颗粒粒径造成不同尾砂料浆间流变性的差异[9]，生产工艺波动使得产出的尾砂颗粒粒径常处于变化的状态，因而造成膏体流变性和触变性的变化[7].小于20 μm 的细颗粒能够形成较强的静电力和胶体作用，随着尾砂逐渐变细，胶体作用会更显著[10].颗粒粒径对尾砂膏体触变性的影响研究尚不丰富，亟需深入研究.

传统尾砂料浆流变学研究更注重稳态条件下颗粒粒径与剪切应力、黏度之间的关系[11].稳态即料浆内部结构不再随剪切时间发生变化的状态.尾砂颗粒粒径和级配是流变性的重要影响因素[12].He 等[13]总结了颗粒粒径和级配对尾砂料浆流动性的影响，发现现存的研究成果差异较大.Leong等[8]分析了平均粒径与屈服应力之间的定量关系，并建立了经验模型.刘晓辉等[14]在研究膏体流变性时发现膏体屈服应力随着细颗粒含量增长呈先增后减的趋势.当料浆所受到的剪切历史发生变化，料浆处于瞬态，此时料浆内部结构随时间变化.瞬态条件下，触变性料浆的流变行为复杂，颗粒粒径影响流变行为的定量分析需要研究者对膏体的触变性有充分的认识.

触变性研究方面的综述丰富[3-4]，也吸引了矿业领域学者的关注[15].经典的触变动力学模型由Moore 提出[16]，尽管触变理论出现较早，近年来仍不断发展[17-18].程海勇[19]研究了颗粒级配对尾砂膏体触变性的影响，但并未深入到触变模型层面.杨柳华[20]研究了尾砂膏体搅拌制备过程中的触变现象，没有涉及触变模型.触变模型研究不仅能够帮助理解料浆的瞬态流变行为，也为数值模拟研究提供理论工具[21].Zhang 等[6]提出了适用于尾砂胶结料浆的触变性模型，能够表征稳态和瞬态条件下料浆触变性的演化规律，为研究颗粒粒径对触变性的影响研究奠定方法基础.

本文将结合触变性演化模型，首先验证不同颗粒粒径时触变性理论体系的有效性.其次，通过恒剪切速率实验得到料浆的剪切应力衰减曲线，利用上述结果验证稳态和瞬态条件下触变性模型.最后，借助数据拟合，建立函数表征剪切速率、颗粒粒径与稳态、瞬态流变参数的关联，实现尾砂膏体触变性定量分析.

1 实验材料和方法

1.1 实验材料

实验用尾砂来自加拿大某铜矿山.本实验采用的研磨设备是棒磨机，利用同一种尾砂制备了四种不同颗粒粒径的样品，通过控制研磨时间来改变尾砂的平均粒径.尾砂粒径利用Malvern 激光粒度仪测得，尾砂粒径分布见图1，颗粒级配信息见表1（D10,D50,D80,D90分别为颗粒体积累计百分比达到10%，50%，80%和90%时的最大粒径，D[4,3]为体积加权平均粒径），本文以颗粒平均粒径为评价指标分析颗粒粒径对触变性的影响，四个样品的体积加权平均粒径分别为37.003、30.676、26.167 和18.617 μm.上述四种粒径的尾砂均为细粒级尾砂，流变性差异显著，有利于分析平均粒径与流变性的关联性.基于ASTM D854-14 标准测得尾砂在20 ℃时的相对密度为2.857.

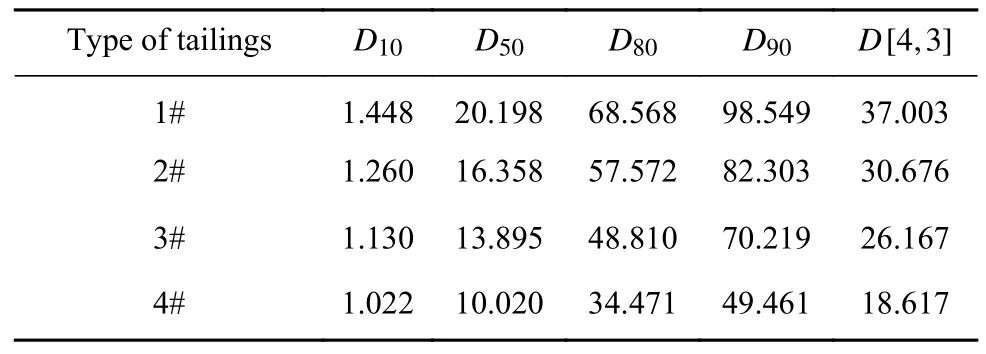
表1 不同粒径尾砂的粒径分布结果Table 1 Particle size distribution details for different tailings

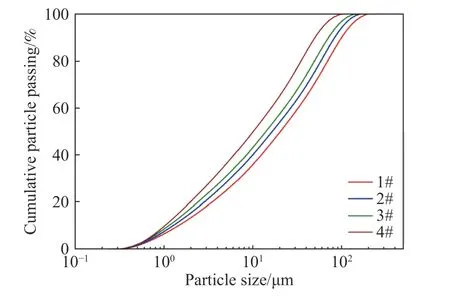
图1 颗粒粒径分布图Fig.1 Particle size distribution of tailings

1.2 实验仪器

实验中使用Thermo Haake VT 550 流变仪，为同轴圆柱测试系统.为了尽可能避免壁面滑移，圆柱形转子表面和样杯内表面都加工有条状细密凸起.转子直径为36.8 mm，高度为60.0 mm；样杯的内径为42.0 mm，转子外表面和样杯内表面之间的间隙宽度为2.6 mm，容器直径和转子直径的比值为1.14.

1.3 实验方法

采用恒剪切速率法获取料浆的剪切应力衰减曲线，该方法能够得到瞬态和稳态条件下的屈服应力[22].水取自实验室的自来水，混合尾砂后制成质量分数为70%的样品.将样品装入测量容器中，剪切历史设置见图2，在剪切速率200 s-1条件下预剪切120 s，静置30 s 后开始测试，每组恒剪切速率测试的时间长度为200 s.预剪切处理是为了保持测试样品具有相同的初始结构状态.实验数据将在Origin 中分析.

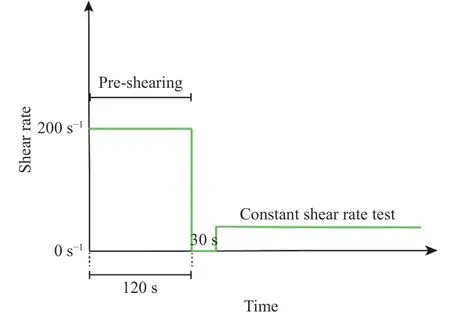
图2 恒剪切速率实验剪切历史设置Fig.2 Set-up of shear history in the constant shear rate test

2 理论

2.1 稳态流变模型

稳态流变模型是表征料浆流变行为的重要工具，稳态流变性与触变性无关，可以作为构建瞬态演化模型的参考基准.常用的稳态流变模型有宾汉姆模型、Herschel-Bulkley（H-B）模型、Casson 模型、幂律模型等.de Souza Mendes 和Thompson[23]在构建弹-黏塑性流体触变模型时采用如下的稳态流变模型：

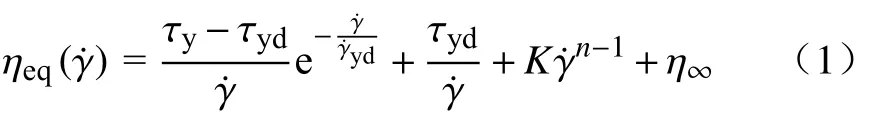
式(1)是在H-B 模型的基础上改进得到，较为复杂.Zhang 等[6]针对高浓度尾砂料浆稳态流变性提出如下的稳态流变模型：

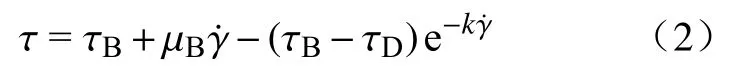
式中：τ为剪切应力，Pa；τB为静态屈服应力，Pa；μB为宾汉姆黏度，Pa·s；τD为动态屈服应力，Pa；k为时变性参数.

2.2 剪切应力衰减模型

剪切应力衰减是指固定剪切速率下料浆剪切应力逐渐下降的现象，这是因为料浆在剪切作用下发生了剪切稀化.描述应力衰减的经典模型由Fiongi 和Shoemaker 提出[24]，即下式：

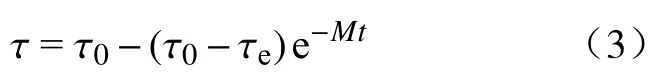
式中：τ0为初始剪切应力，Pa；τe为稳态剪切应力，Pa；M为指数；t为时间，s.

本文将以式(2)和式(3)分别表征料浆的稳态流变性和恒剪切速率条件下应力衰减特性，据此构建料浆触变性模型.

2.3 触变性演化模型

引入结构参数 λ表征瞬态条件下料浆内部的结构状态，结构参数的取值范围为[0,1].在式(2)基础上，定义触变性尾砂料浆的稳态结构参数 λe的表达式为

引入稳态结构参数 λe后，稳态流变模型即可改写为

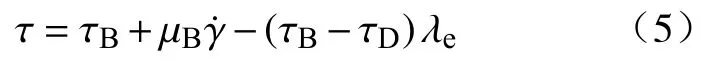
瞬态条件下料浆的剪切应力的表达式为：

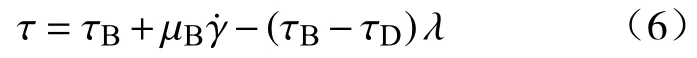
结合式(4)，结构参数 λ的动力学演化方程为：

根据上述触变理论模型，得到F-S 模型的一般形式，即

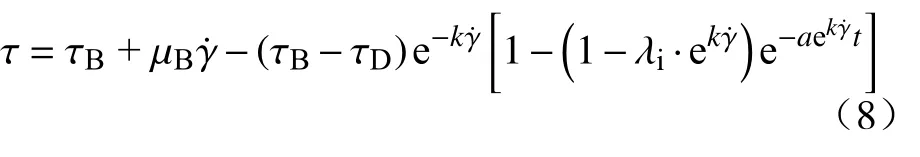
上式中，静态屈服应力 τB、动态屈服应力 τD、塑性黏度 μB、时变性参数k、初始结构参数 λi都是已知的.只需要确定参数a和剪切速率 γ˙的关系，式(8)即可描述恒剪切速率下的剪切应力衰减现象.a和具有式(9)的函数关系，式(9)的适用性可以参见Zhang 等[6]的工作，拟合效果将在后面讨论.

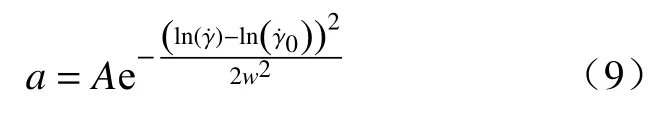
式中，A,w,是拟合参数.

式(6)、(7)、(9)共同组成了高浓度尾砂料浆的触变本构模型.

3 实验结果与分析

3.1 稳态流变性

不同平均粒径尾砂的稳态流变曲线见图3.可以看出，在低剪切速率区间，料浆的稳态剪切应力τe随着剪切速率增加而显著增长；当剪切速率超过一定值时，流变曲线的斜率变小并趋近于恒定，剪切应力和剪切速率逐渐呈现显著线性关系，此时料浆黏度也趋近于剪切速率无穷大时的黏度.利用式(2)拟合实验数据，每组尾砂料浆的拟合参数见表2，拟合曲线的校正决定系数（Adjusted R-Square）均超过0.977，说明该模型的拟合效果较理想.Tangsathitkulchai[25]研究表明，当颗粒粒径减小时，料浆在不同剪切速率下的剪切应力均呈增长趋势，与本文得到的稳态流变性演化规律吻合，但仍然缺少颗粒粒径影响稳态流变性的定性表征研究.

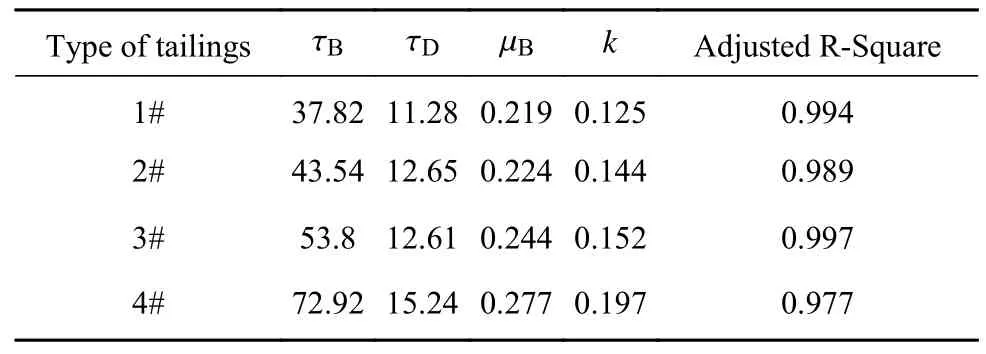
表2 稳态流变曲线拟合参数Table 2 Fit parameters of equilibrium rheological curves

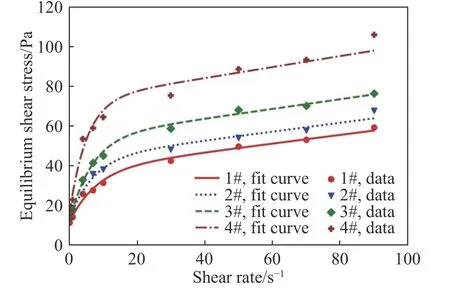
图3 不同颗粒粒径尾砂料浆的稳态流变曲线Fig.3 Equilibrium rheological curves of tailings suspensions at various particle sizes

3.2 颗粒粒径对稳态流变性的影响

颗粒粒径对料浆流变性具有显著的影响，Leong等[8]在研究氧化锆胶体流变性中发现，料浆在等电点处的最大屈服应力τymax与浓度 φv、颗粒平均粒径存在下述关系：

式中，κ为拟合参数.由式(10)可知，τymax与成正比例关系.类比于上述关系，将表2 中各拟合参数和之间的关系绘制在图4 中，拟合方程分别为：

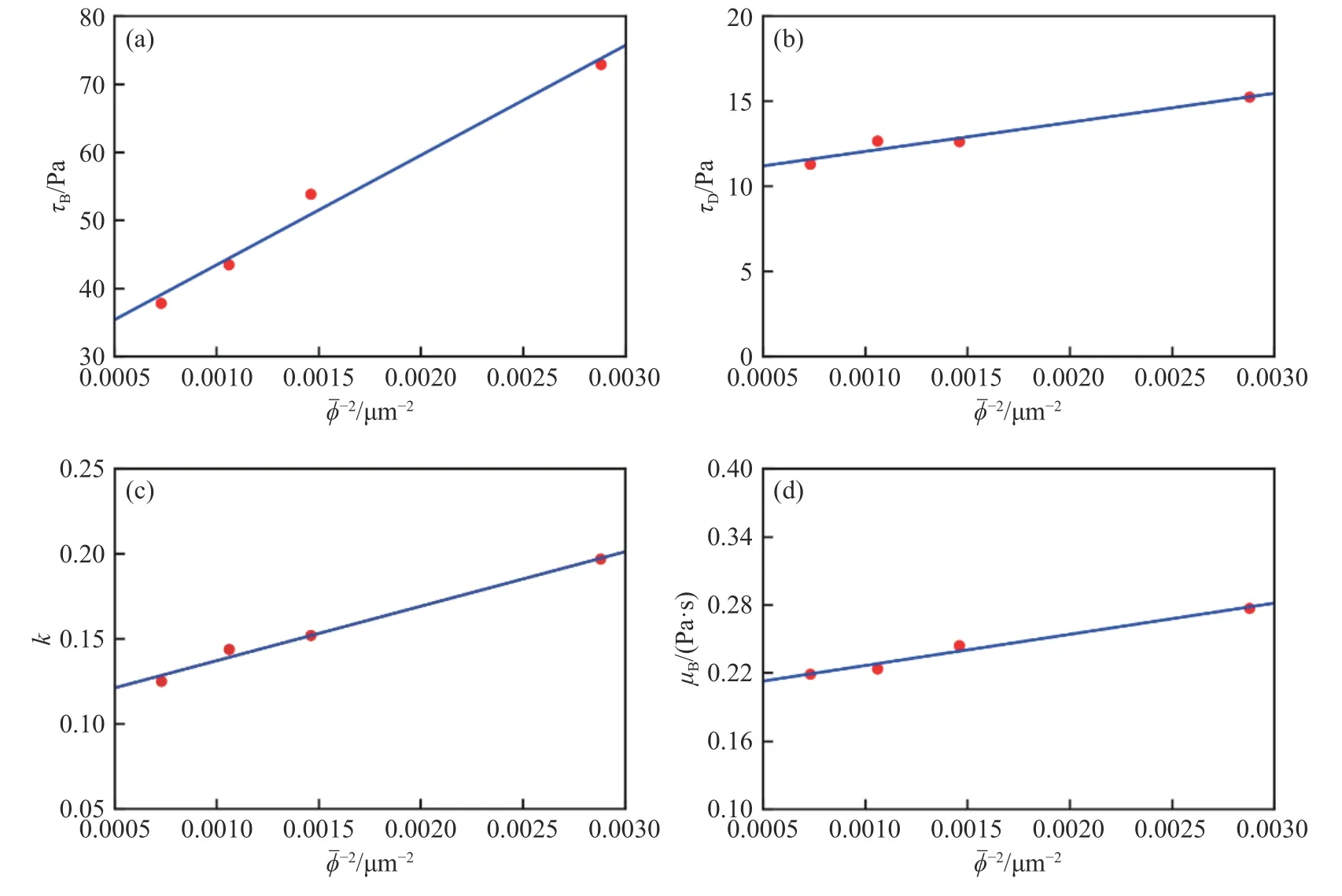
图4 稳态流变模型各参数与之间的关系Fig.4 Relationships between parameters of the proposed equilibrium model and

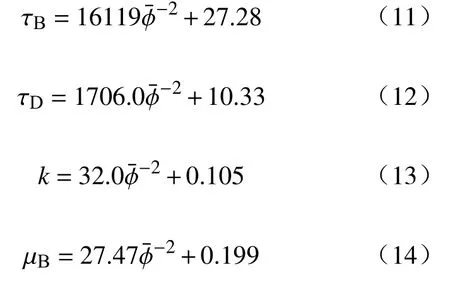
拟合方程的Adjusted R-Square 分别为0.975、0.929、0.981 和0.969，拟合效果理想.因此，基于可以构建适用性较好的稳态流变预测模型，将式(11)～(14)与式(2)联立即可分析稳态条件下和对稳态剪切应力的影响.

稳态剪切应力与剪切速率、平均粒径二者的关系曲面见图5.由图可知，颗粒粒径的波动导致料浆剪切应力的显著变化.当颗粒平均粒径较小时，同等剪切速率条件下的稳态剪切应力更大.平均粒径减小导致比表面积增加，更多水吸附在颗粒表面而参与流动的水分减少，因而屈服应力或黏度均有所增长[7].在制备高浓度尾砂料浆时，要考虑尾砂粒径的变化，通过调整浓度等改善料浆的流动性.

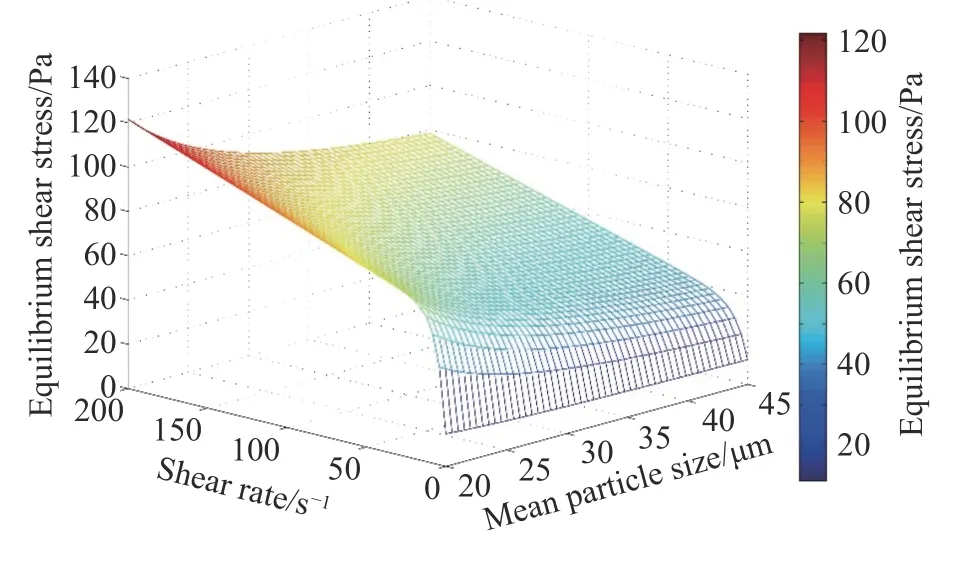
图5 不同颗粒平均粒径和剪切速率下料浆稳态剪切应力曲面图Fig.5 Surface plot of equilibrium shear stress of suspensions at various mean particle sizes and shear rates

3.3 膏体触变性与模型验证

图6 为不同平均粒径下尾砂料浆瞬态剪切应力的演化规律.剪切速率在0.1 s-1和90 s-1之间取值.由图6 可以看出，当剪切速率较低时，料浆均出现显著的剪切应力衰减现象；剪切速率增大后，剪切应力衰减现象逐渐减弱，甚至消失.这是因为料浆结构参数在低剪切速率区间能够发生较大幅度的变化，而当剪切速率很大时，结构参数均趋近于0，变化幅度可忽略不计.

将不同平均粒径下参数a和剪切速率的关系绘制在图7 中.用式(9)拟合参数a的演化曲线，拟合结果的Adjusted R-Square 均大于0.967，拟合效果较好.可以看出，随着 γ˙的增加，参数a呈现先增加后减小的趋势.随着颗粒平均粒径的减小，参数a的曲线峰值增加.结合图6 可知，样品4#的平均粒径最小，当剪切速率为0.5 s-1时，该样品剪切应力衰减速率最大.因此，a可以作为衡量料浆触变性的重要指标.

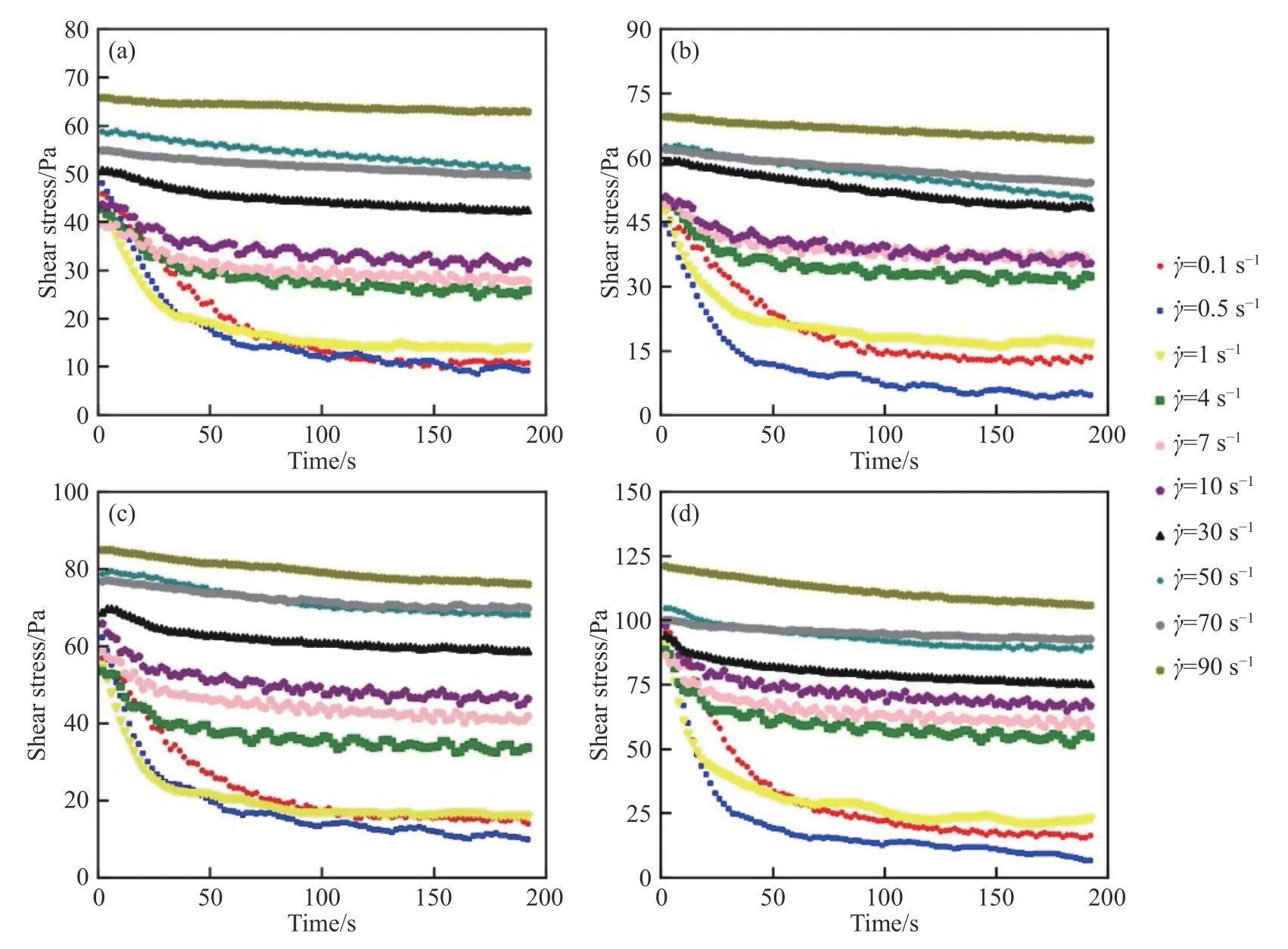
图6 不同剪切速率下料浆剪切应力衰减曲线.（a）1#；（b）2#；（c）3#；（d）4#Fig.6 Shear stress decay curves at various shear rates: (a) 1#;(b) 2#;(c) 3#;(d) 4#

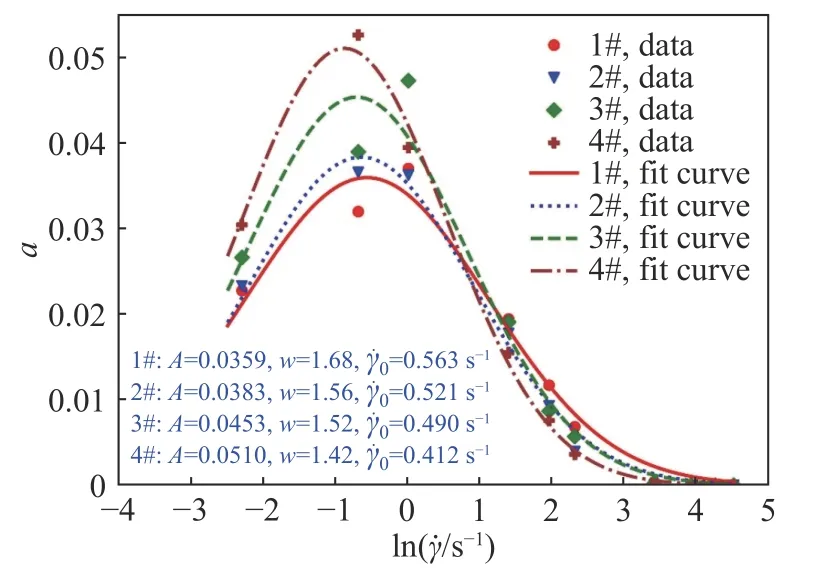
图7 参数a 与ln的关系曲线Fig.7 Relationships of parameter aandln

触变性模型在预测胶结充填料浆剪切应力时表现较好[6].图8 为不同平均粒径时尾砂料浆恒剪切实验数据和触变模型预测结果的比较.由误差分析可知，颗粒平均粒径在20～37 μm 之间变化时，多数数据点位于10%误差以内.需要注意的是，部分数据误差较大，这是因为剪切应力衰减曲线仅测量一次，测量的偶然性导致偏差.触变模型参数通过多个剪切速率下的剪切应力衰减曲线获得，能够一定程度降低测量误差的影响.总体上看，触变模型得到了四种不同平均粒径尾砂料浆的验证，说明推荐的触变动力学模型适用性好.

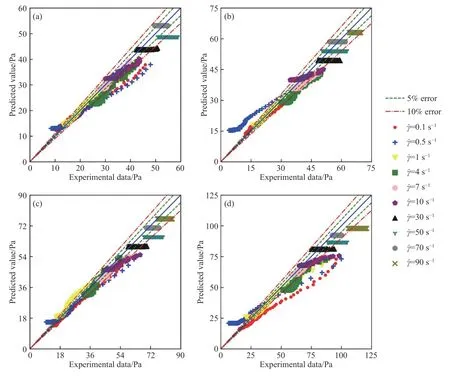
图8 四种尾砂不同剪切速率下实验值和预测值的比较.（a）1#；（b）2#；（c）3#；（d）4#Fig.8 Comparison between experimental and predicted shear stress at various shear rates s for the four kinds of tailings: (a) 1#;(b) 2#;(c) 3#;(d) 4#

3.4 颗粒粒径对瞬态流变性的影响

瞬态流变性相较于稳态流变性，不同之处在于引入了时间变量，利用结构参数的变化分析流变参数如瞬态剪切应力的演化规律.此处选取恒剪切速率时的应力演化为对象进行分析，剪切速率设为0.1 s-1，仅考虑时间、颗粒平均粒径对瞬态剪切应力的影响.料浆在200 s-1剪切速率条件下基本达到稳态后，λi和颗粒平均粒径之间的关系式为：

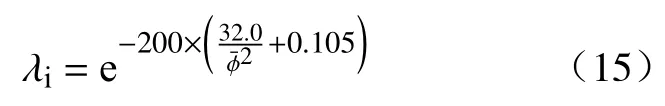
A、w、ln和颗粒平均粒径之间的关系曲线见图9，拟合方程见式(16)～(18)，其Adjusted RSquare 分别为0.932、0.974 和0.960.

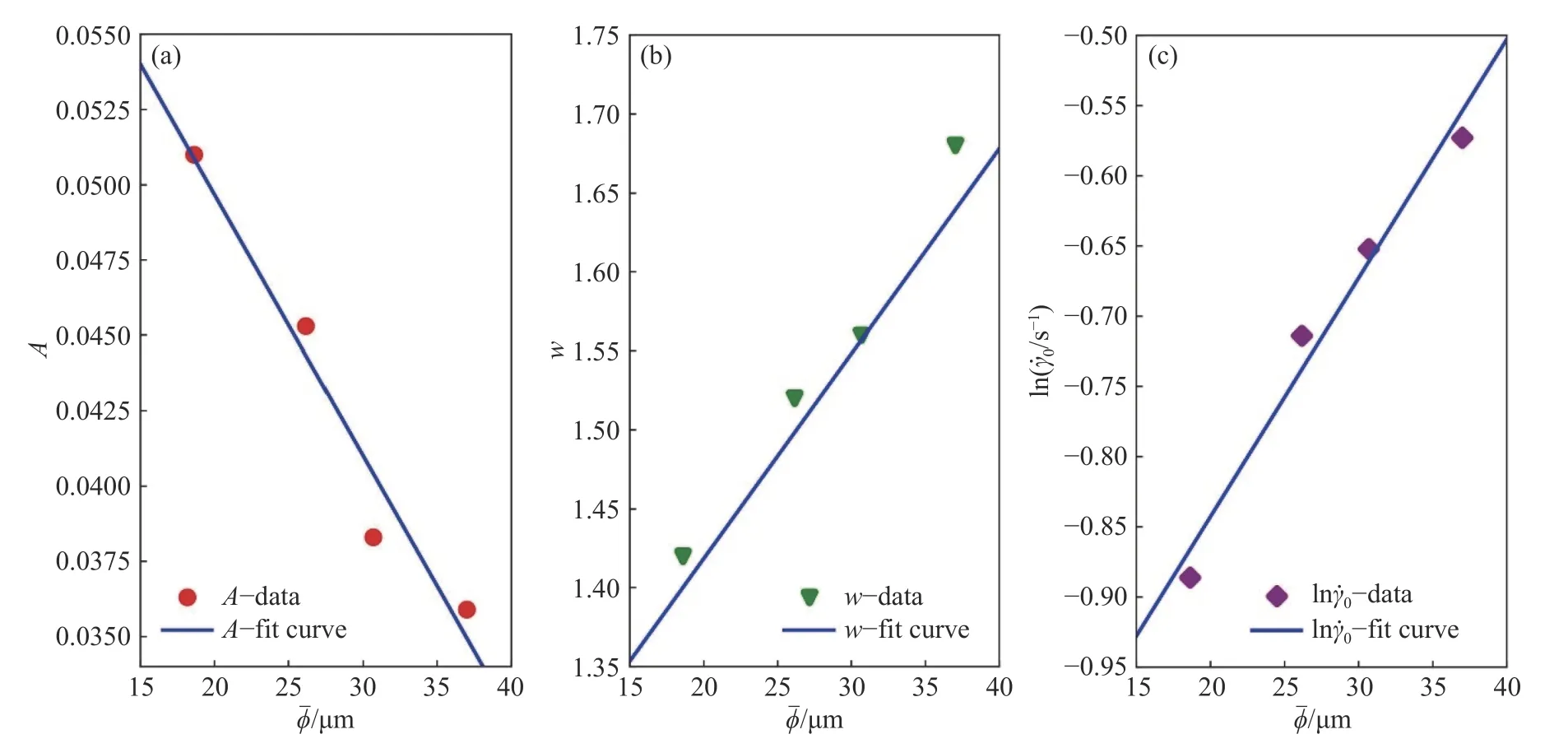
图9 拟合参数与平均粒径的关系曲线.（a）A；（b）w；（c）lnFig.9 Relationships of fit parameter and mean particle size: (a) A;(b) w;(c)ln

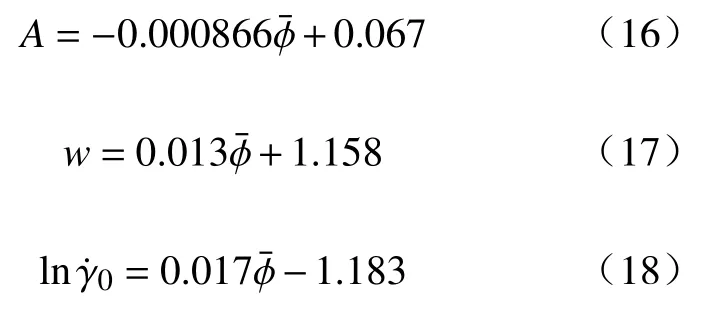
在式(8)、(9)、(15)～(18)基础上，得到恒剪切速率条件下时间、颗粒平均粒径与料浆瞬态剪切应力的关系曲面图，即图10.可以看出，料浆在充分预剪切后，颗粒粒径对初始剪切应力的影响更显著.料浆预剪切时经历了很高的剪切速率，料浆内部的结构充分破坏，相应的结构参数 λ也趋近于0.当料浆在低剪切速率下实验时，剪切速率不变的情况下，屈服应力有较大差异，而稳态时的剪切应力差别不显著，这是因为料浆结构参数在t=0时刻对剪切应力影响显著.尽管不同平均粒径时的料浆均发生了剪切应力衰减，颗粒较粗料浆的应力衰减幅度远小于含有更细颗粒的料浆.这说明，平均粒径减小的情况下，尾砂膏体的触变性会增强.质量分数相同时，颗粒更细的料浆具有更大的比表面积，颗粒间可流动的水减少，颗粒更容易形成絮团.因此，在较高的剪切破坏作用下，细颗粒尾砂的絮团破坏过程所需要的能量更高[26]，破坏絮团时需要克服的颗粒间作用力直接影响触变性的强弱，造成了初始时刻屈服应力的差异.

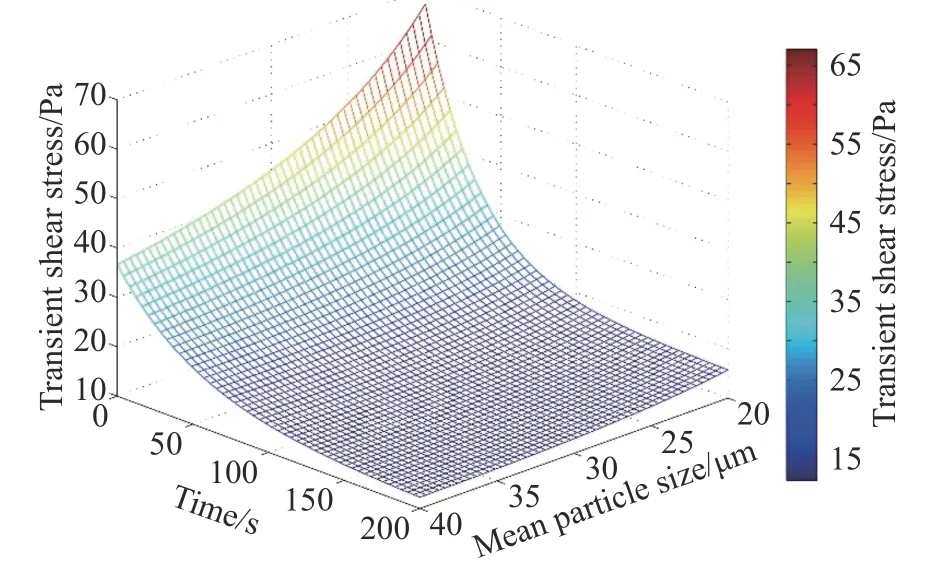
图10 恒剪切速率条件下时间、颗粒平均粒径与瞬态剪切应力的关系曲面图Fig.10 Three-dimensional graph of transient shear stress under the effects of time and mean particle size at constant shear rates

4 结论

本文研究了不同颗粒粒径尾砂膏体的触变性，从稳态和瞬态两个角度定量分析了尾砂料浆流变特性，得到的主要结论包括：

(1) 高浓度尾砂料浆在低剪切速率时呈显著的剪切应力衰减现象，根据新稳态流变模型分析可知，静态屈服应力、动态屈服应力、宾汉姆黏度和时变性参数均与线性相关；

(2) 恒剪切速率实验验证了触变模型的有效性，在该模型基础上推导恒剪切速率条件下剪切应力衰减函数，不同平均粒径下的预测结果与实验数据吻合；

(3) 根据触变模型分析了恒定剪切速率条件下瞬态剪切应力演化规律，揭示了平均粒径、时间双因素耦合作用下料浆瞬态剪切应力演化规律，定量表征了平均粒径、时间对瞬态剪切应力的影响.