基于离散粒子群优化算法的多值属性系统故障诊断策略

田恒， 许荣滨， 姜艳红， 张文虎， 邓四二

(1.河南科技大学 机电工程学院， 河南 洛阳 471003； 2.浙江五洲新春集团股份有限公司， 浙江 绍兴 312500；3.中浙高铁轴承有限公司， 浙江 衢州 324407)

0 引言

故障诊断策略是保障卫星导航、武器装备等高端产品安全运行的关键，其在产品测试性方面的重要性愈加显著[1-3]。诊断策略主要通过研究最优序列寻优算法，实现最经济地诊断隔离系统故障。现有的序列寻优算法大都是面向二值系统，该类算法通过对二值矩阵处理，得出最优的测试序列。然而，实际工程中，大多数装备或系统是多值属性系统(MVAS)，对应的测试被是多值测试。目前已有许多专家学者开始研究MVAS的故障诊断策略，并取得了一些成果。

黄以锋[4-5]等在信息熵(IG)算法和Rollout算法的基础上，扩展了测试的结果，改进算法的启发式，提出基于IG算法和Rollout算法，实现了MVAS故障诊断策略的寻优。文献[6]在Growing算法的基础上，扩展了启发式，提出基于Growing算法的MVAS测试序列优化算法。在二值系统中，此类算法仅能获取近似最优结果，即使对其启发算式扩展，用在MVAS中，也无法获得最优结果。为解决上述问题，专家学者研究利用群智能算法搜索MVAS的诊断策略。粒子群优化(PSO)算法是群智能算法的重要内容，能够解决连续域及离散域方面的问题[7-9]。

Yang等[10]在考虑故障诊断率和隔离率的基础上，提出了一种贪婪算法确定最优测试集，利用离散二进制PSO算法搜索故障的最优测试序列。陈希祥等[11]结合二进制PSO算法和遗传算法，提出一种混合算法，搜索最小完备测试集。Hou等[12]在传统模糊PSO算法的基础上改进了粒子群智能算法，通过信息流可测性建模优化测试集，提出一种测试点优化算法。为解决不完全测试条件下近似最优测试点集合的选择问题，Deng等[13]建立了启发式函数，设计了PSO算法的适应度函数。在考虑故障隔离率的基础上，Lv等[14]将混沌离散粒子群(DPSO)算法与故障诊断相结合，提出一种选择测试的优化模型，然后运用离散PSO算法解决二值系统故障诊断隔离的问题。Lian等[15]将测试序列寻优转化为群体多维空间的排序问题，然后基于量子行为的PSO算法，提出一种搜索故障测试序列的方法。Ma等[16]在离散PSO算法的基础上，根据测试选择的特点，设置一种适应度函数，并为了避免早熟添加迭代权重，实现了二值系统的故障诊断隔离。文献[17]利用改进的蚁群算法搜索MVAS的测试序列。王伟等[18]提出一种基于人工智能的搜索剪枝技术，寻找MVAS的最优故障诊断策略。

上述算法能找到测试序列，但有一些缺陷：1)最小完备测试集中不一定是最优的，导致诊断策略不是最优的，而且集合中测试被频繁使用，使得费用升高；2)算法大都通过降低故障检测率和故障隔离率以减少期望费用，导致无法诊断隔离所有故障，使得诊断结果较差；3)上述算法的启发式仅能处理二值系统，无法解决MVAS的诊断策略问题。

本文为解决上述问题，首先通过重塑离散PSO算法，模拟测试序列寻优过程，将故障诊断策略问题与离散PSO算法结合。然后设置离散粒子群的自身认知和社会知识阶段的运算规则，提出PSO-TS算法，最后实验验证PSO-TS算法的正确性和稳定性。

1 诊断策略公式化

诊断策略主要是利用寻优算法对依赖矩阵(D矩阵)进行处理，进而获取期望费用最小测试序列。为寻找上述测试序列，获得合适的诊断策略，需要将故障诊断策略进行公式化处理。因此，引入文献[17]和文献[19]的多值D矩阵及五元组。

1.1 多值D矩阵

多值D矩阵表示MVAS中测试与故障的关联关系，其中行向量表示故障，列表示测试项，元素dij(i=0,1,…,m，j=1,2,…,n，m、n分别为故障状态数和测试数)为测试值，如表1所示。表1中，tj为测试，fi为故障状态，其中f0表示无故障，p(fi)为故障fi的先验概率，dij表示采用测试tj检测故障fi时，若出现dij对应的测试值，表明可能出现故障fi，设定dij∈{0，1，2，…}。

表1 MVAS的依赖矩阵Table 1 Dependency-matrix of MVAS

1.2 诊断策略的描述

利用五元组(F，P，T，C，D)表示MVAS的故障和先验概率等内容，其中各组的含义如下：

1)F是系统故障集，F={f0，…，fi，…，fm}。

2)P是先验概率集，P={p(f0)，…，p(fi)，…，p(fm)}，该集合中所有元素之和为1。系统无故障概率较大，设p(f0)在0.5～0.8随机取值。

3)T是测试集，T={t1，t2，…，tj，…，tn}，tj的测试值为a，其与dij的取值范围相同。

4)C是测试费用集，C={c1，c2，…，cj，…，cn}，cj为使用测试ti所花费的成本，本文设其为无量纲的数值。

5)D是(m+1)×n维的矩阵，D=[dij](m+1)×n，表征测试与故障的关联关系。

MAVS确定最优诊断策略的过程是指寻找具有最优测试序列的过程，而最优的评价标准为测试期望测试费用最小，该费用的计算公式为

(1)

式中：Tfi为故障fi的测试序列。

因此，选择使(1)式取最小值为最优测试序列，即为MVAS的最优诊断策略。

2 新离散PSO算法

离散PSO算法能处理旅行商推销员(TSP)问题，而TSP问题是离散的非确定性完全(NP-C)问题。故障诊断策略问题也是离散的，同样属于NP-C问题。因此，通过合理的转化，离散PSO算法可以用来寻找最优的故障诊断策略，即最优的测试序列。

2.1 离散PSO算法的过程重塑

为实现离散PSO算法在MVAS故障诊断策略中的应用，将算法的基本概念(如粒子、自身认知、社会知识等)与测试序列的含义进行一一对应，同时引入交换序的概念，如表2所示。

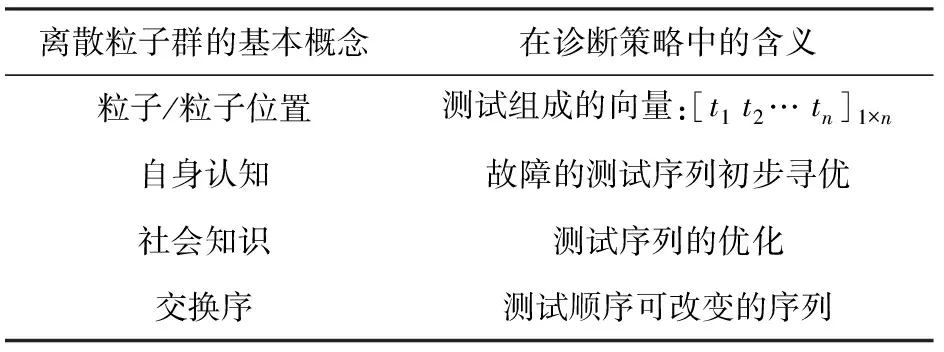
表2 离散PSO算法基本概念与诊断策略对应关系Table 2 Corresponding relationship between basic concepts of DPSO and diagnosis strategy

假设上述粒子为散落在n维空间里的坐标点，其坐标为[t1t2…tn]1×n的一组向量，其中的元素是测试集T中的测试。离散PSO算法的重要环节重新表述：

1)自身认知阶段，粒子通过某种计算规则为模糊故障子集选择测试，然后将被选的测试进行排序，而未被选择的测试按照原来的顺序补充到向量中的后续坐标，则得到新粒子坐标，记为向量Pi，表示经过自身认知计算之后粒子i的坐标；

综上所述，离散PSO算法与MVAS的故障诊断策略可以融合，但还需要为其自身认知和社会知识设置计算规则。

2.2 粒子的自身认知

假设某测试tj将故障模糊集x分割为K个故障模糊子集{xj1，…，xjK}。p(xjk)为故障模糊子集xjk的先验概率；fg为故障，是模糊子集xjk中的元素；p(fg)为故障fg的先验概率。粒子群自身认知阶段测试寻优的计算规则为

(2)

(3)

(4)

MI(x,tj)=I(x,tj)/p(x,tj)

(5)

式中：p(x)为故障子集x的先验概率；p(x，tj)表示运用测试tj检测故障集x时，所有故障子集的基数与其概率的乘积；IG(x，tj)表示运用测试tj检测故障集x的IG。

(2)式～(5)式可以对测试进行排序，但在一个计算过程之后，所有粒子测试序列都是相同的。这是因为上述算式对粒子中所有测试进行排序，即使粒子中测试初始顺序不同，但是并不会影响排序结果，所有粒子中测试顺序完全一样的，降低了粒子的多样性，无法找到最优解。因此，需要限制上述公式对测试集搜索与排序的范围，增加粒子多样性。

为解决上述问题，引入“邻域”的概念，设定在自身认知阶段上述公式仅能在向量的某个区域内寻找最优测试。该区域即为邻域，设定规则如下：

1)向量的第1个元素为邻域的起点；

2)该区域内测试数量即为邻域大小，设置为2q，q为当前模糊集个数。

矢量控制系统是将飞机方向舵取消，通过一个矢量电机座将电机和舵机连接起来安装在机身上，再利用舵机的转动来控制电机的左右转动，从而改变电机提供的拉力方向(即拉力线)或推力方向，通过拉力线或者推力线方向的改变，进而控制飞机的左右转向。取消方向舵舵面，然后将舵面和垂尾固定在一起形成新的垂直尾翼保持方向安定。本设计不仅仅适用于前拉式飞机，同样适用于尾推式飞机。

对于规模相同的二值系统和多值系统，二值系统需要更多测试，因此用二值系统来确定邻域大小。二值系统中，若对q个模糊子集诊断隔离，则总共需要用2q-1个测试(包含已经使用和将要使用的测试)。但是初始时，系统只有1个模糊故障集，其邻域大小为1，即仅有一个测试，无法实现测试选择。因此，设定邻域大小为2q，其对多值系统而言包含足够多的测试。另外，由于测试集中测试数量是有限的，所以邻域最大不能超过测试集中的测试总数。

2.3 社会知识与粒子的交换序

社会知识阶段，粒子通过改变其内部测试的位置实现朝最优粒子移动，其过程是将粒子中的测试位置进行转换，使粒子相应位置上的测试改成最优粒子相同位置上的测试。因此，需要重新计算，判断新粒子是否使目标函数取最优值。为便于实现粒子内部测试位置的改变，引入交换序的概念。

交换序(ta，tb)表示测试ta与tb在粒子向量中的位置进行互换。当位置互换后，若当前循环中还需更换测试顺序时，ta的位置不能变，但tb可以改变。

根据重塑的离散PSO算法过程，结合自身认知和社会知识的计算规则，引入粒子的更新公式：

(6)

VGi=PG-Pi

(7)

(8)

一般情况下，PG中的测试只有部分被使用，因此，可将使用的测试组成交换序。另外，ε的值越大算法运行时间越短，但是会影响最终结果，导致无法获得最优诊断策略。

2.4 PSO算法详细步骤

在重塑离散PSO算法的基础上，提出了测试序列寻优算法，记为PSO-TS算法，流程图如图1所示。PSO-TS算法详细实现步骤如下：

1)初始化五元组(F，P，T，C，D)和最大循环次数Lmax。若F中故障数量≤1，则算法结束。

2)随机产生N个粒子，每个粒子为一组1×n维向量，其元素为T中的测试，元素顺序随机排列。

3) 重复以下步骤，直到循环次数等于Lmax或获得使得(1)式获得最优值。

①设定邻域，根据(2)式～(5)式选择测试，获得故障的测试序列，确定N个粒子的新位置。

②采用(1)式计算①中测试序列的期望测试费用J，选择最小值对应的粒子，设其为最优粒子PG。

③利用(6)式、(7)式和(8)式计算出所有交换序。

④随机取ε个交换序，根据交换序的更换规则，更新粒子所有的非最优粒子。

4) 输出最终的期望测试费用和测试序列。

3 实例验证

3.1 算例验证

以文献[6]和文献[19]中某型电站除氧器系统的多值D矩阵为例(见表3)，验证算法的正确性。

运用PSO-TS算法处理该矩阵，详细步骤如下：

1)设定粒子群规模为24，即随机产生24组向量，设置最大循环次数为20次；

2)自身认知阶段，利用(2)式～(5)式得到20个新粒子；基于(1)式，选择成本最小的粒子为最优粒子PG，PG=[12 5 10 7 3 11 9 1 6 4 8 13 14 2]；

3)社会知识阶段，其他粒子与最优粒子的序列对比，找到相同位置上不同的测试，确定交换序；通过改变粒子中测试顺序，实现测试序列寻优，完成粒子朝着最优粒子位置移动过程，进而优化诊断策略。以某粒子[12 7 3 1 11 10 6 13 8 9 2 4 5 14]为例说明，通过与PG对比，确定有(5，7)、(10，3)、(7，1)等13组交换序，随机选取其中一个(10，3)，将该粒子上的t10与t3所在位置交换，从而形成新的粒子[12 7 10 1 11 3 6 13 8 9 2 4 5 14]。

表3 电站除氧器MVAS的多值D矩阵Table 3 Multi-valued D matrix of a power plant deaerator

4)重复上述步骤，直至寻找到较优结果或者达到最大循环次数。

在上述过程中，新粒子与PG距离减少，体现了测试序列的优化，而且后续的循环过程PG不断改变，粒子群也在不断变化，从而找到较优的诊断策略。

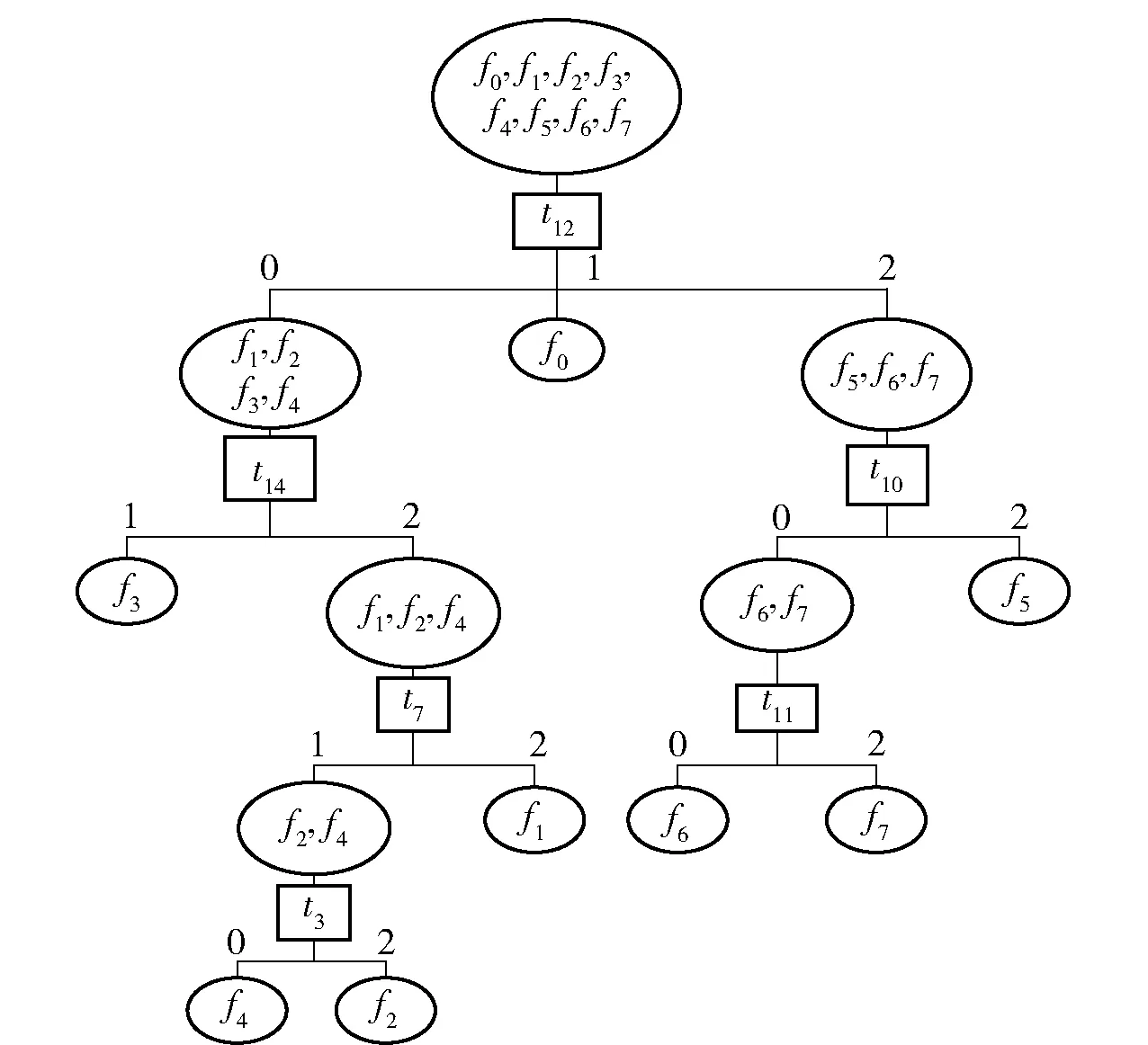
图2 基于PSO-TS算法的故障诊断树Fig.2 Diagnosis tree based on PSO-TS algorithm

最后输出测试序列，以诊断树的形式展示结果，如图2所示。基于(1)式，PSO-TS算法的结果为3.339 8，这与文献[6]和多值Rollout算法的结果相同。

3.2 仿真验证

为验证算法的通用性和稳定性，在MATLAB软件平台上编写PSO-TS算法，同时编写文献[4-5]中的多值Rollout和多值IG算法，简记为MV-Rollout、MV-IG。引入平均期望测试费用(avgJ)和平均运行时间(avgRt)来评价上述算法的优劣。

(9)

(10)

式中：Ji为某算法第i次计算的期望测试费用；Q为多值D矩阵被计算的总次数；Rti为某算法第i次的运行总时间。

随机产生一组矩阵，模拟多值D矩阵，其维数如表4所示，矩阵元素dij在{0，1，2，3}中随机取值。当矩阵规模较大时，PSO-TS算法消耗时间较多，因此设定每个矩阵计算15次。在每次计算过程中，测试费用在区间[1 2]中随机取值。每个多值D矩阵的行对应为系统故障，第1行表示无故障状态。所有故障的先验概率均随机产生，总和为1，而无故障状态的先验概率在0.5～0.8之间随机取值。设置PSO-TS算法的粒子规模为故障数的3倍，最大循环次数为20，当PG中的测试小于10个时，交换序个数ε取值为1，否则ε=⎣(|PG|/4)」。

采用PSO-TS、MV-Rollout和MV-IG算法的处理上述矩阵，按照(9)式和(10)式计算avgJ和avgRt，结果如表4所示。展示维数为100×100的多值D矩阵15次的结果，如图3所示。

表4 PSO-TS、MV-Rollout和MV-IG算法的avgJ和avgRt对比Table 4 Comparison of avgJ and avgRt values for PSO-TS, MV-Rollout, and MV-IG

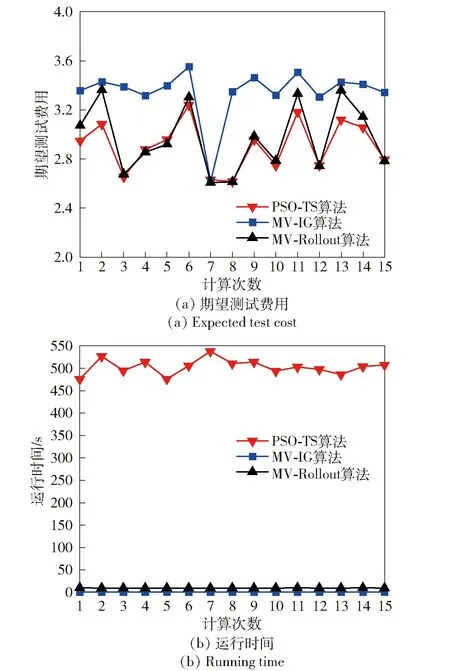
图3 基于PSO-TS、MV-Rollout和MV-IG结果Fig.3 Calculation results based on PSO-TS、 MV-Rollout and MV-IG

由表4和图3可知，PSO-TS算法的大部分avgJ小于MV-IG和MV-Rollout算法的结果。这是因为PSO-TS算法基于邻域、社会知识等实现内部迭代，具有随机性和指向性，能获得更优的结果。

MV-IG算法的avgJ大于PSO-TS和MV-Rollout算法的结果，这是因为MV-IG属于一步向前寻优的算法，仅能找到局部最优的测试，而PSO-TS和MV-Rollout算法可以通过不断地迭代，进而搜索到较优的测试。

PSO-TS算法的avgRt大于MV-IG和MV-Rollout算法的结果。这是因为PSO-TS算法在自身认知阶段需要对所有粒子进行计算，而且所有粒子都将会迭代，导致算法运行时间增加。同时，因为随着方阵规模增加，粒子群的规模不断增加，导致PSO-TS算法的avgRt逐渐增加。

4 结论

本文在研究传统离散PSO算法的基础上，改进了粒子群算法的自我认知阶段和社会知识阶段的计算规则，提出了PSO-TS算法。得出主要结论如下：

1)重塑了离散PSO算法，运用离散PSO算法模拟MVAS的测试序列寻优过程，实现了离散PSO算法与MVAS故障诊断策略的融合。

2)根据测试序列寻优算法的约束函数，设置了自身认知和社会知识阶段的运算规则，并引入了邻域概念。该方式既保障了粒子的多样性，又保留算法随机性和指向性，使其拥有了进化能力，改善了诊断结果。

3)实例和随机仿真实验结果表明：与MV-Rollout和MV-IG算法相比，PSO-TS的期望测试费用少，能够获得较优的诊断策略，但是运行时间较长。