高鲁棒性两阶段激光雷达-惯性测量单元外参在线标定算法

林 鑫 张 捷 冯景怡 孟 杰 王书亭

1.华中科技大学能源与动力工程学院，武汉，4300742.驭势科技有限公司基础平台研发部，北京，1024003.华中科技大学机械科学与工程学院，武汉，430074

0 引言

激光雷达(laser detection and ranging, LiDAR)和惯性测量单元(inertial measurement unit, IMU)是即时定位与建图 (simultaneous localization and mapping, SLAM)技术中常见的传感器配置，也是自动驾驶传感器的主流组合。LiDAR测距范围大，精度可达厘米级，但在雨雪等恶劣环境下测量可靠性差，不适用于旷阔的环境；IMU通常分为加速度计和陀螺仪，可以提供载体的加速度和角加速度，它不依赖于环境场景，但在长时间下存在累积误差。LiDAR与IMU在自动驾驶任务中可以优劣互补，因此，基于LiDAR和IMU融合的定位算法[1-3]成为近年来的研究热点。LiDAR的定位结果基于LiDAR坐标系，而LiDAR定位过程需要校正点云的运动畸变，因此需要从IMU获得高频运动信息。对于所有的融合算法来说，为了提高最终输出定位结果的精度，均需要尽可能准确地标定传感器之间的坐标系转换关系。几何变换的估计过程称为外参标定，即估计不同传感器坐标系之间相对六自由度(即旋转和平移)变换。人工测量传感器之间的相对平移和旋转是不准确的，有时也是难以实现的。手眼标定[4-5]是一个众所周知的传感器校准方法，本文将手眼标定的传感器模型应用到自动驾驶车辆的LiDAR与IMU传感器组合上，LiDAR通常安装在汽车顶部附近，IMU通常安装在汽车后桥的垂直中心线前面。

手眼标定是一种重要的标定方法[6-8]，广泛应用于具有自我运动估计能力的传感器的标定。HORAUD等[8]将手眼标定经典公式AX=XB应用到相机和LiDAR等更广泛的传感器配置中，并开发了一个通用的数学框架来解决手眼标定问题。为了标定LiDAR与IMU之间的外参，GENTIL等[9]提出了一种LiDAR-IMU传感器系统外参标定的概率框架，基于IMU数据插值的预积分，可以消除三维点云的运动失真，并根据点云的点到面距离对平面进行环境拟合，构建优化方程。吴昱晗等[10]通过将点云转化为全局坐标系，在逐帧聚类后匹配点云中心，并优化残差函数来估计最优的六自由度外参，但由于同一类型目标点云的观测范围不同，聚类结果在帧与帧之间存在差异，故无法对该方法的准确性进行定量评价。杨超等[11]提出基于非线性优化的里程计与LiDAR外参的在线标定算法，根据优化方式求取较为精确的激光雷达位姿信息。彭梦等[12]针对2D LiDAR和摄像机最小解标定方法多解问题，在最小解标定过程中提出改进措施以提高真解命中率和标定精度。JIAO等[13]通过对齐每个传感器的估计运动来进行自动初始化的手眼校准，然后通过最小化由特征点到平面构成的残差函数，使用基于外观的方法对所得参数进行二次优化。为了关联IMU和LiDAR的测量数据与外参，需要在数据层面将它们联系起来。受视觉惯性工作[14]的启发，YE等[2]设计了紧耦合LiDAR-IMU融合的方法，使用原始IMU数据和LiDAR测量来优化整个系统的状态，其中包括可获得初始外参的系统初始化和持续滑动窗口优化外参，但是该工作没有考虑到如何解决退化运动时的系统初始化。对于包含大量近似平面运动的无人驾驶汽车，IMU很难在六个自由度上都获得足够的激励，这就导致了无人驾驶汽车中LiDAR-IMU外参标定困难。

为了解决无人驾驶汽车中传感器噪声和退化运动导致LiDAR-IMU外参标定失败的问题，本文提出了一种高鲁棒性两阶段LiDAR-IMU外参在线标定算法。第一阶段是旋转外参解析解初值计算，通过剔除外点来去除退化的传感器数据，先对预数据集筛选出具有一定的旋转增量激励，并且IMU里程计旋转增量和LiDAR里程计旋转增量中满足角度差小于阈值的、离散的里程计对来构建只包含旋转分量的手眼标定方程组，同时对整个数据集以滑动窗口的形式，对手眼标定方程组多次求解解析解，最后以奇异值分解(SVD)中的第三大与第四大奇异值的比值来进行多解加权。第二阶段是非线性滑窗在线迭代优化，最小化包含外参的残差函数，以旋转解析解为初值滑动窗口迭代优化六自由度外参，使外参快速收敛，并在退化运动和错误历史约束过大时固定外参，避免外参退化。本文标定算法对不完美和退化的传感器数据具有鲁棒性，在无初值情况下也能在线标定外参。

1 基本原理

1.1 手眼标定模型

图1 不同位置下里程计增量关系

(1)

(2)

式中，α为偏航角(yaw)；β为俯仰角(pitch)；γ为横摇角(roll)；c表示cos；s表示sin。

通过计算平移部分和旋转部分6个参数，可以得到IMU坐标系与LiDAR坐标系的六自由度变换关系。

在本文的外参标定算法中，只考虑对应的IMU里程计增量和LiDAR里程计增量的旋转部分。在系统还未初始化时，通常会忽略IMU的偏差，这个偏差包括加速度计的偏差和陀螺仪的偏差。IMU作为一个包含旋转状态和平移状态的估计器，其旋转量是陀螺仪数据的一阶积分，而平移量是加速度计数据的二阶积分，因此，在加速度计的偏差和陀螺仪的偏差都没有获得修正时，二阶积分求得的平移量远远大于一阶积分所得的旋转量。同时，依据传感器特性，陀螺仪偏差相对于加速度计偏差更为稳定，累积误差也更小，因此，对于IMU而言，旋转量相对于平移量的累积误差更小。

图2 只考虑旋转分量的手眼标定模型示意图

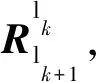
(3)

将式(3)用四元数表示为

(4)

其中，⊗表示两个四元数之间的乘法运算。由式(4)可得

(5)

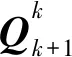
(6)

其中，qw为四元数实部，四元数q和其虚部qv分别表示为

(7)

[qv]×为虚部向量的反对称矩阵：

(8)

对于N对相对旋转的测量值，可获得超定的线性方程：

(9)

(10)

(11)

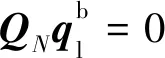
QN=UΣVT

(12)

1.2 含外参的非线性滑窗迭代优化

在即时定位与建图过程中，随着关键帧和路标点的增多，后端优化的计算效率会不断下降，为了避免这种情况，使用滑动窗口算法将待优化的关键帧的数量限制在一定范围内，以控制后端优化的规模，固定一些历史轨迹，仅对当前时刻附近的一些轨迹进行优化，如图3所示。

图3 滑动窗口优化算法

当新的测量约束出现时，滑动窗口将包含新的状态，并在窗口中忽略最老的状态。通过最小化以马氏范数表示的代价函数：

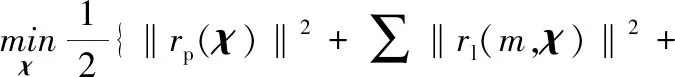
(13)

得到状态χ的最大后验估计。其中，rp(χ)表示边缘化先验残差，rl(m,χ)表示相对LiDAR扫描的点到线面约束的残差，rb(z,χ)表示IMU预积分约束的残差。滑动窗口内所有的状态量定义为χ：

(14)

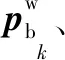
(15)

代价函数(式(13))为非线性最小二乘形式，采用高斯-牛顿算法求解。

2 改进算法

2.1 算法框架

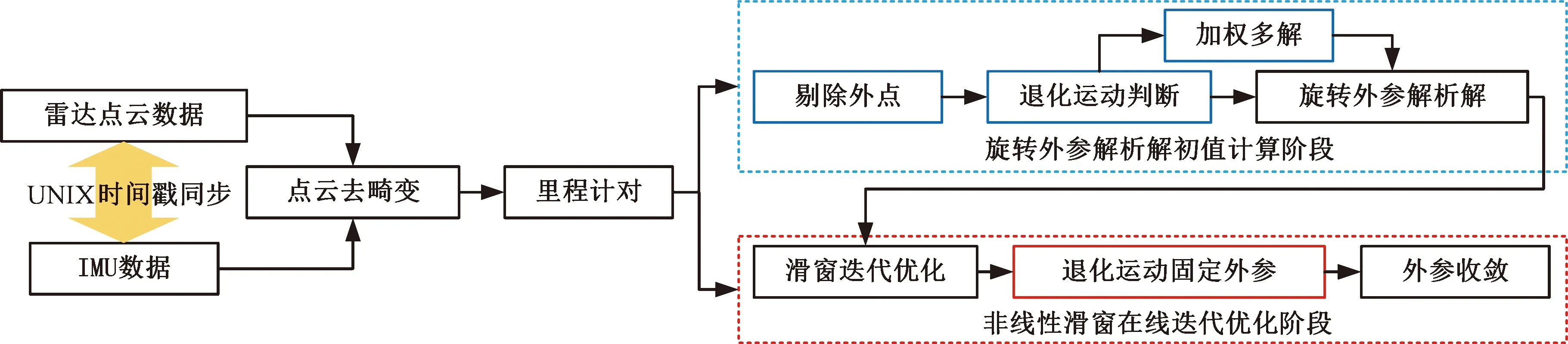
图4 两阶段LiDAR-IMU外参标定流程框架

2.2 旋转外参解析解初值计算改进

2.2.1剔除外点的手眼标定模型

图5 两个里程计增量夹角

图6 旋转外参解析解初值计算改进框架图

另外，在只考虑旋转部分手眼标定模型中，观察旋转部分约束方程发现，当传感器的运动接近直线运动时，旋转部分的矩阵R趋近于单位矩阵，当R恰好等于单位矩阵时，旋转部分的约束方程退化，即有

(16)

2.2.2手眼标定模型求解的判断条件改进

σ3/σ4>threshold

(17)

与原始算法中单纯以第三大奇异值σ3>0.25的绝对阈值相比，考虑到最佳最小二乘解的求解条件，奇异值σ3/σ4比值的相对阈值threshold对包含退化运动的数据更具鲁棒性，更能反映手眼方程组内的运动状态。

2.3 非线性滑窗在线迭代优化改进

2.3.1两阶段LiDAR-IMU外参标定算法框架图

图7 两阶段LiDAR-IMU外参标定算法框架图

2.3.2退化运动时的固定外参策略

非线性滑窗在线迭代优化阶段也会遇到一些较为平缓的运动序列，为此，本文设置了在遇到退化运动(如静止或者匀速运动)时触发固定外参的策略，即

(18)

(19)

当pmean小于一定的阈值时，说明此时的运动状态是静止的或者匀速的，属于退化运动，这时外参的某些状态量处于不可观情况。为了避免第一阶段获得的精确的解析解初始值在迭代优化过程中被带偏，陷入局部极小值，需要进行固定外参的操作。第二个条件是在系统刚初始化成功时，初始的点云地图还未收敛，点云的匹配效果较差，出现较多的误匹配，导致优化中含有错误的历史残差，在这时迭代优化外参，将导致解析解初始值偏离，而这部分历史残差应当先由窗口内的IMU状态来进行调整，直到系统较为稳定时再开始启动微调外参。具体方案为判断rcost的值：

rcost=rp(χ)/(rl(m,χ)+rb(z,χ))

(20)

若rcost大于阈值，说明错误的历史约束比较大，则固定外参。进一步地，若rcost远大于阈值，说明错误的历史约束过大了，则固定外参的同时重置历史约束残差。

3 实验分析

3.1 实验设计

3.1.1实验平台与传感器数据预处理

如图8所示，该实验车辆含有一个Velodyne VLP-16型号的激光雷达与一个Xsens MTi-100型号的IMU。在车辆视图中，激光雷达坐标系是l系统，l系统原点位于激光雷达结构的中心，它的X轴指向车辆前进方向，其Y轴垂直于X轴指向车辆前进方向的左边，Z轴垂直于X、Y轴向上。IMU载体坐标系的定义是b系统，b系统原点位于IMU的中心，它的X轴也是指向车辆前进方向，其Y轴指向车辆前进方向的左边，Z轴垂直于X、Y轴向上。为方便观察和比较，在后续的实验结果分析时，将使用yaw、pitch和roll来分析LiDAR-IMU之间的旋转，并将之前所有可用的外参的平均值作为后续标定实验的目标值。

图8 车载实验平台

在获取LiDAR和IMU两个传感器的数据信息后，首先做的是数据同步。LiDAR点云频率为10 Hz，即获取的位置信息更新频率为10 Hz，而IMU点云频率数据为200 Hz，两者均采用UNIX时间戳机制，记录结果自1970年1月1日(UTC时间)开始。因为不能保证找到具有相同时间戳的数据，因此通过时间插值来实现同步对齐。同步对齐后，可以得到同一时间序列的两个传感器的位姿信息。

3.1.2可观性分析与运动要求

对于IMU传感器来说，各状态量耦合程度较高，直观上难以确定各状态量是否能够得到有效估计，通过可观性分析[15]可有效掌握系统对各状态量的估计情况，同时有助于提出相应的改进方案。为了获得可靠的平移校准，需要至少两轴旋转以及随机平移。单轴旋转将导致平移校准沿旋转轴变得不可观。可靠的空间校准的最小运动要求是至少一个全局轴平移和双轴旋转，为了最大限度地使标定过程中LiDAR-IMU外参的各个量可观，车辆需要有X、Y轴上的旋转运动，即包含roll和pitch分量上的运动激励，因此，采集的预数据集会包含“∞”环的运动序列，并含有上下斜坡的运动序列，使其包含Z轴方向的运动激励，最后预数据集还需要超过3 min的驾驶时间，以确保在旋转外参解析解初值计算阶段有满足本文算法筛选的可用IMU数据进行校准，尽量避免IMU数据完全退化，确保LiDAR-IMU外参参数的六自由度可观性。

3.2 旋转外参解析解初值计算改进对比实验

3.2.1改进后的手眼标定方程组窗口大小

表1 不同手眼标定方程组窗口大小下外参标定误差

该实验的评价指标为不同手眼标定方程组窗口大小获得旋转外参yaw、pitch和roll的标定结果与目标值的误差均值，与目标值的偏差越小，该窗口大小越好。从6组不同窗口设置的标定结果中可以看出，以10帧的滑动窗口大小来求解手眼标定方程组的旋转外参最小二乘解的误差均值最小，最小为0.775°，对应yaw、pitch和roll三个角的误差为(1.190°,0.625°,0.510°)。该实验的结论为：在以上6组的窗口大小配置中，手眼标定方程组最佳窗口大小设置为10帧，在满足旋转外参解析解标定结果精确度的前提下，还能实现以小规模(10帧大小)的手眼标定方程组来减小求解复杂度，加快求解速度。

另外，为了对比剔除外点算法和原始算法构建的手眼标定方程旋转外参解析解多解误差分布情况，将它们的旋转外参yaw、pitch和roll多解误差绘制成图9所示的箱线图，从图中可以看出，剔除外点算法的旋转外参解析解的yaw、pitch和roll三个角的误差外点数量要远少于原始算法，同时误差均值也更接近零，说明剔除外点算法的旋转外参解析解稳定性和精确度更高，对退化传感器数据的鲁棒性更高。

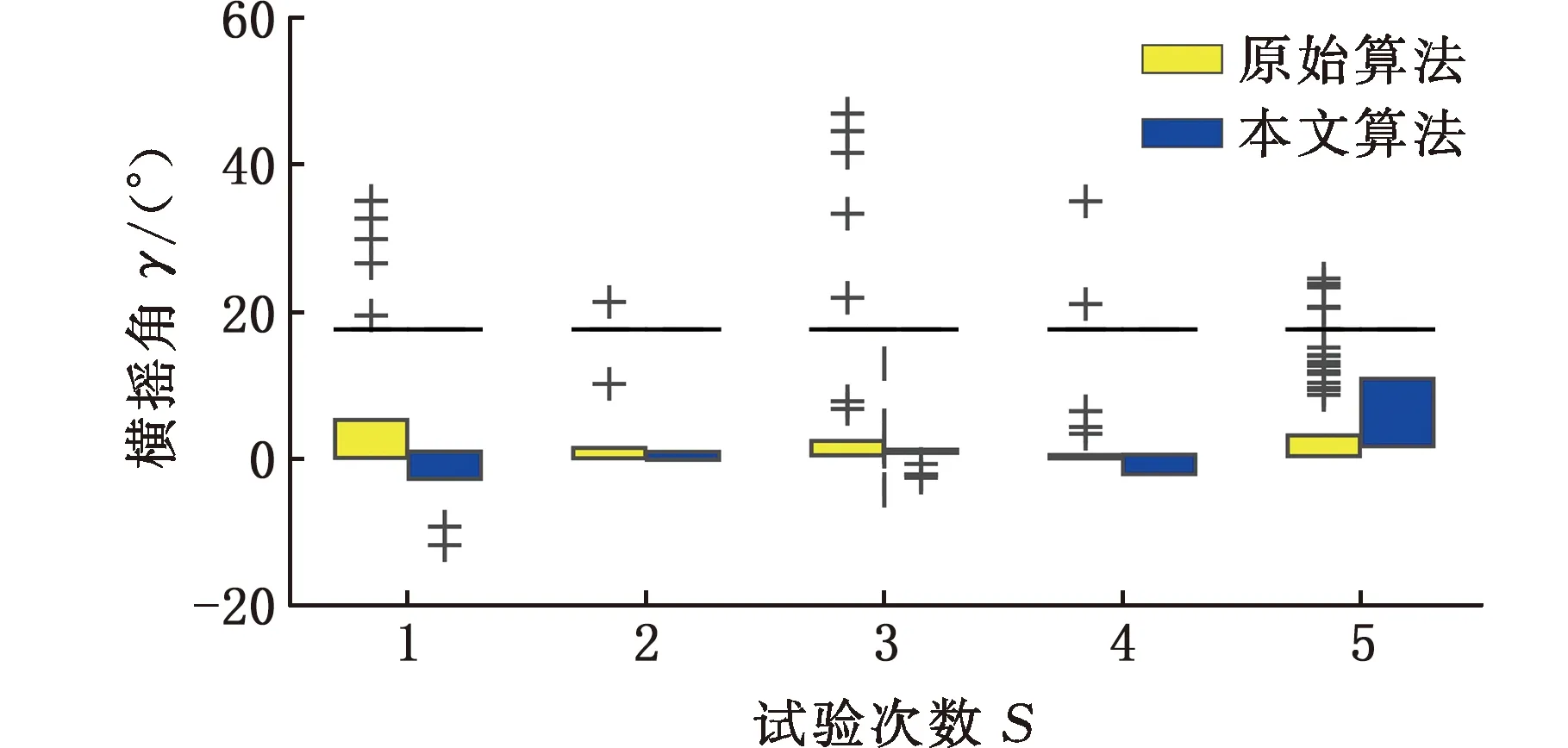
图9 剔除外点算法与原始算法误差分布对比

3.2.2旋转外参解析解多解加权方式

由于第一阶段改进为以滑动窗口的形式，以10帧的窗口大小多次求解旋转外参解析解，并以奇异值分解的奇异值矩阵中的第三大与第四大奇异值σ3/σ4的比值作为阈值进行筛选解析解来判断运动激励，因此为了基于数据集的最大化成功率计算旋转外参解析解，本文以奇异值σ3/σ4的比值来加权每次求解的旋转外参解析解结果。为了将第一阶段中窗口滑动过程中的所有手眼标定方程组求解的解析解都利用起来，以达到基于预数据集的最大成功率获得最佳的旋转外参解析解初值的目的，下面通过实验来确定最佳的加权方式。

以奇异值σ3/σ4的比值大于2.5作为筛选阈值，采用8种不同的加权方法，分别对4组不同运动序列的数据集进行32组实验，来探索8种不同的加权方法中，手眼标定方程组旋转外参解析解多解的最佳加权方式，实验结果如表2所示。

该实验的评价指标为以不同手眼标定方程组旋转外参解析解的加权方式获得旋转外参yaw、pitch和roll结果与目标值的误差均值，误差均值越小，说明该加权方式越好。由表2可得，由加权方式D的误差均值最小，最小为2.578°，对应yaw、pitch和roll三个角的误差为(5.669°,0.799°,1.265°)，因此，解析解多解的最佳加权方式为D，即筛选多解中满足σ3/σ4>2.5的解，并以奇异值σ3/σ4作为各个解的权重加权求和，误差均值最小。

表2 不同加权方式下的外参标定误差

3.3 非线性滑窗迭代优化改进对比实验

为了避免迭代优化中一些退化运动造成系统状态量偏离，本文在出现退化运动时选择固定外参，不进行外参优化，最大化利用求解手眼方程组的解析解第一阶段提供的良好的初始值，以避免陷入优化的局部极小值。因此，在实验场地中含有直道和弯道的地方进行在线标定实验，与原始算法对比，以验证固定外参策略的有效性。

如图10所示，通过非线性优化中外参迭代优化过程的对比，观察旋转外参yaw、pitch和roll的变化可以得出：本文带有固定外参策略的改进算法的旋转和平移外参量在迭代到40帧左右便收敛至零误差附近，而原始算法在迭代到200帧以后才逐渐收敛，且Z方向上的平移和yaw方向的旋转误差较大。因此，两阶段LiDAR-IMU外参在线标定算法收敛速度快于原始算法收敛速度，可有效避免外参在非线性迭代优化中陷入局部最小值。

(a)平移外参数

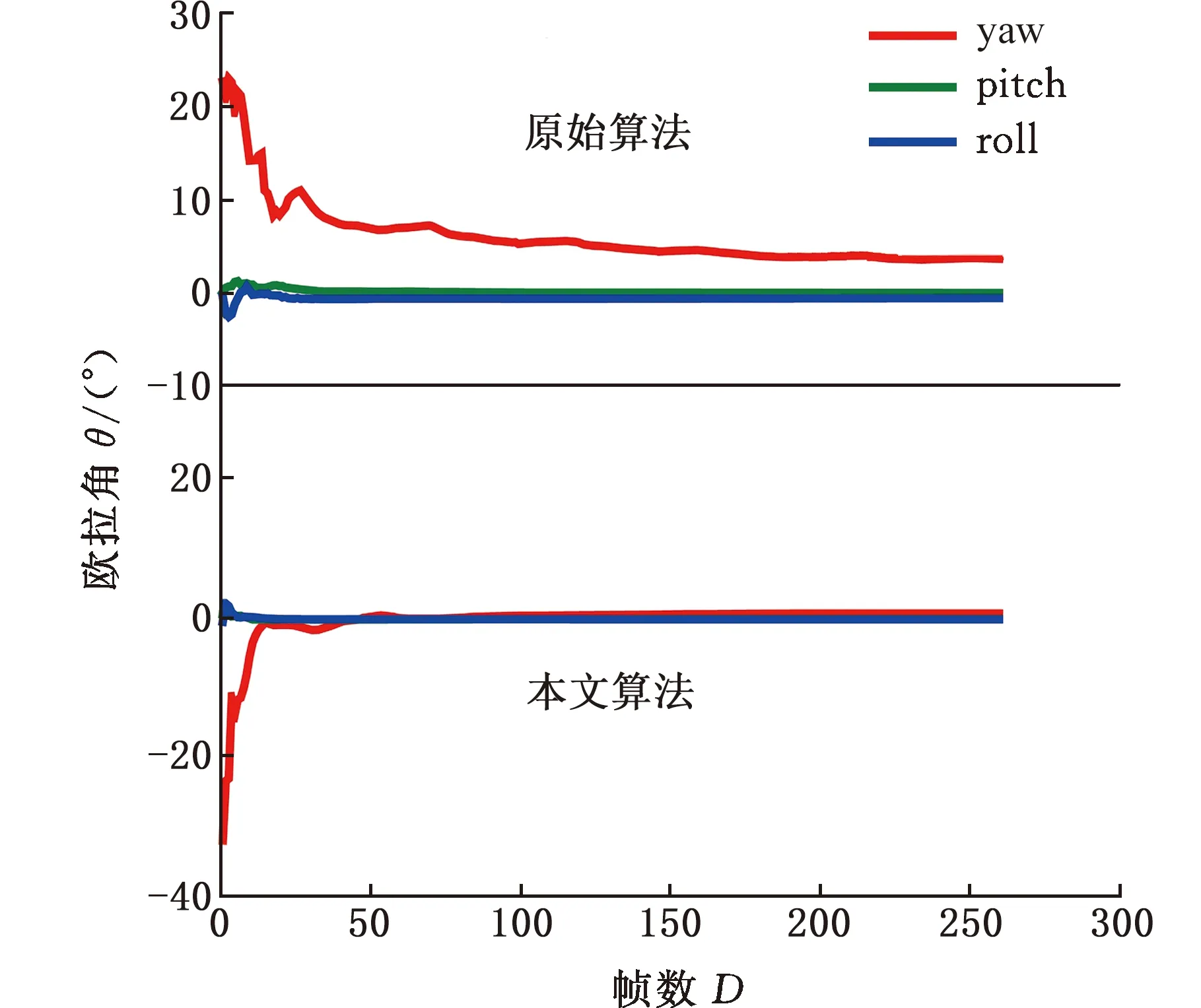
(b)欧拉角旋转外参数图10 固定外参算法与原始算法外参变化对比

3.4 3D点云重建可视化综合验证

在第二阶段的紧耦合SLAM过程中，除了在线标定LiDAR-IMU之间的外参，该阶段也会进行点云地图的构建。为了直观地比较本文改进算法的外参标定成功率和精度，与原始算法进行同一数据集的建图效果可视化对比，分别在地点A、B中进行实验，3D点云重建结果如图11所示。

(a)地点A-原始算法 (b)地点A-本文算法

(c)地点B-原始算法 (d)地点B-本文算法图11 3D点云重建可视化对比

在地点A的即时定位与建图过程中，原始算法标定结果的误差太大，外参陷入局部极小值，无法在迭代中恢复，构建的点云地图漂移，标定失败。而本文算法标定结果的误差小，外参迭代收敛至真值附近，构建的点云地图紧凑规整，标定成功。在地点B的即时定位与建图过程中两个算法都标定成功，但是原始算法点云地图的左下部和右下部红色框内含有重影，未完全收敛，而本文算法重建的点云地图在这两处都收敛，地图质量优于原始算法地图质量。因此，在本文所测试的数据集中，两阶段LiDAR-IMU外参在线标定算法对退化的传感器数据具有鲁棒性，能够有效提高外参标定成功率，在即时定位与建图过程中，本文算法在标定后的3D点云建图成功率和精度均优于原始算法。

4 结论

为了解决无人驾驶中传感器噪声和退化运动导致LiDAR-IMU外参标定失败的问题，本文提出了一种高鲁棒性两阶段LiDAR-IMU外参在线标定框架，第一阶段是旋转外参解析解初值计算，第二阶段是非线性滑窗在线迭代优化。与原始框架相比，其鲁棒性改进方面可以总结为以下几点：

(1)第一阶段通过剔除外点去除退化的传感器数据来构建手眼标定方程组，在剔除外点算法的旋转外参解析解多解中，yaw、pitch和roll三个角的误差外点的数量要远少于原始算法，提高了标定算法对包含退化传感器数据的鲁棒性。

(2)通过滑动窗口多次求解解析解初值来筛选多解中满足相对阈值σ3/σ4>2.5的解，并以奇异值σ3/σ4作为各个解的权重加权求和，旋转外参yaw、pitch和roll的误差均值最小，最小为2.578°。

(3)第二阶段非线性滑窗在线迭代优化时设置了固定外参的策略，在退化运动和错误历史约束过大时固定外参，避免了第一阶段获得优化初值漂移过大，陷入局部最小值。

(4)将原始算法的三维点云重建结果与两阶段LiDAR-IMU外参在线标定算法的重建结果进行对比，本文所改进的算法对退化的传感器数据具有鲁棒性，提高了标定成功率和精度。