多孔挡板影响液体晃荡冲击压力特征的研究

沈民民 孙船斌 童宝宏 侯童珅

1.安徽工业大学机械工程学院，马鞍山，2430322.特种重载机器人安徽省重点实验室，马鞍山，243032

0 引言

船舶在波浪中航行会激励液舱内的液体产生强烈的瞬时冲击以及剧烈的晃荡[1-2]，液体晃荡引起的局部瞬态高压可能会损坏液舱结构[3]，甚至影响船舶运动姿态，尤其是当外部激励频率在液舱的共振频率附近时[4]，液舱结构损坏可能更为严重，所以对流体晃荡问题的研究主要关注在固有频率附近冲击载荷随频率变化的规律[5]。在液舱中加入挡板，利用挡板的阻尼作用可以有效抑制冲击压力，并增强液舱本身的结构强度，但挡板的加入不仅会增加舱体自重、缩小载液容积，还存在受流体冲击而损坏的风险[6]，因此，挡板结构既要保证抑制液体晃荡，又要降低成本与风险。

晃荡问题一直是液舱设计的关键。FALTINSEN等[7-8]基于线性势流理论对液舱在晃荡幅值较小的情况进行了研究；张海涛等[9]采用非线性振动解析方法求出了小幅激励容器所受晃动力的解析近似解。然而目前对大幅晃荡过程的研究较少。由于液体在大振幅激励下会伴随着复杂的水动力现象[10]，比如波浪的翻卷、破碎以及气泡夹带等现象，强烈的非线性和不稳定行为让理论解析法对剧烈晃荡的预测和捕捉存在局限性，因此目前主要通过模型试验与数值模拟对剧烈晃荡进行研究[11-12]。

气体与液体均具有可压缩性，二者相互作用会导致晃荡冲击压力幅值较大且冲击时间较短[13]。当垂直波正面撞击舱壁时，会出现气泡夹带，导致瞬时压力峰值产生[14-15]。XUE等[16]发现挡板附近的流体会由于边缘效应产生涡旋；孙龙刚等[17]基于Q准则对复杂的涡旋流动进行了表征。对冲击信号处理有利于分析晃荡过程，XUE等[18]基于FFT(fast Fourier transformation)发现，尽管挡板位置不同，但主要响应频率都是其外激励频率和其倍频。杨志勋等[19]采用的HHT(Hilbert-Huang transform)方法充分反映出了晃荡冲击过程中的时频特性。

挡板可以有效抑制晃荡现象。国内外学者已经对各类挡板结构进行了大量研究。ABRAMSON[20]首次提出在航天器中安装挡板来抑制发动机燃料的晃动；GOUDARZI等[21]发现，为抑制宽度较大容器中的晃荡，垂直穿孔挡板的阻尼效果更好；POGULURI等[22]进一步对晃荡过程中垂直方孔板筛引起的射流和波浪破碎进行了研究。YU等[23]比较了固度比(挡板固体面积与挡板总面积的比值)分别为0.4、0.6与0.9的垂直方孔板筛抑制晃荡自由液面高度的效果，研究表明固度比为0.6的板筛效果更好，且在液舱中设置两块垂直挡板能更有效地抑制高频激励引起的晃荡。上述研究多针对方形孔隙，但随着方孔密度变化，板筛上的方孔存在加工复杂、应力集中度高，以及屈曲承载能力较低等问题[24]，而圆孔对该问题有所改善。目前，关于大振幅激励、多孔结构挡板影响下，波浪翻卷及破碎后的气泡掺入引起的随机性冲击压力随外激励频率变化的规律仍鲜有报道，多孔结构挡板对冲击压力在时域及频域的影响仍有待完善。

针对上述问题，本文研究多孔结构挡板对液体剧烈晃荡的抑制过程。通过构建大振幅水平激励试验平台开展扫频试验，研究大振幅激励下冲击压力的时域和频域特性，并从挡板结构和涡旋强度方面解释冲击压力特征产生差异的原因。

1 试验设置与冲击压力响应规律

1.1 试验平台

基于水平激励试验平台开展试验研究，该平台由曲柄滑块机构施加谐波激励运动平台，运动平台通过导轨、滑块实现运动。将液舱模型固定在运动平台上，利用采集与控制装置完成对信号的采集与处理，如图1所示。伺服电机控制运动平台的激励频率，调节速度控制器实现运动平台按照指定的规律运动。

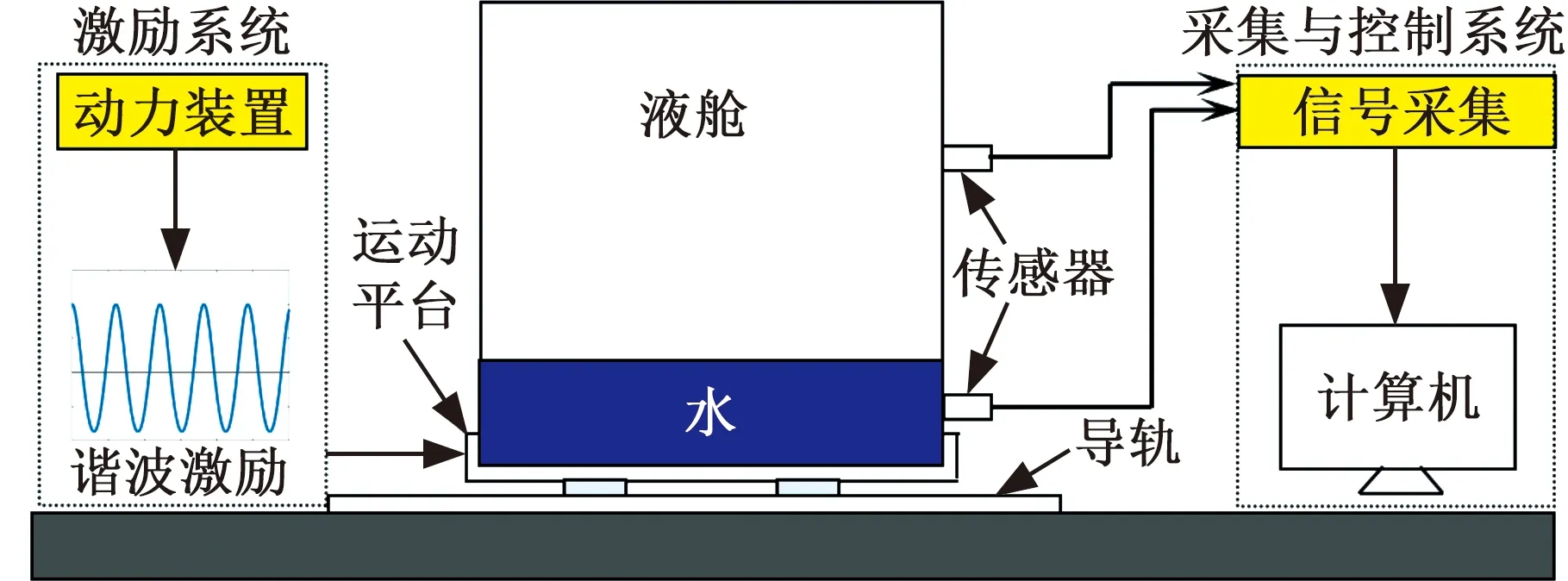
(a)试验设备工作原理示意图

(b)动力装置 (c)传感器安装位置 (d)信号采集仪图1 试验设备工作原理图及主要仪器实物图

液舱采用透明有机玻璃，液舱内部长宽高分别为400 mm、200 mm及400 mm。曲柄滑块机构中连杆长度为500 mm。薛米安等[25]对液深为90 mm时无挡板影响下液舱中液体晃动现象进行了分析，本文亦将液深设定为90 mm，探究同一液深下多孔挡板对液体晃荡的影响。多孔挡板的长度和高度分别为200 mm和400 mm，孔径为40 mm，孔距为48 mm，多孔挡板的固度比Sn=0.6，距离液舱壁面的距离为125 mm，如图2所示。

图2 多孔挡板模型示意图

为记录液体晃荡对舱壁的压力，在液舱运动方向舱壁的中心线处安装液压传感器，液压传感器距离舱底的距离为30 mm，可确保剧烈晃荡时能够监测到液体对舱壁的冲击压力。每次试验前需要先校准传感器，运动平台回到初始位置，并保证液面平静，确保试验数据真实可靠。

1.2 试验工况

以正弦运动激励试验平台，使液舱往复运动。试验平台的水平运动正弦激励速度函数为

(1)

式中，A为振幅，mm；ω为激励角频率，rad/s；t为时间，s。

根据势流理论的假设，二维矩形液舱的固有频率计算公式[8]为

(2)

kn=(2n-1)π/ln=0,1,2,…

式中，ωn为n阶固有频率；g为重力加速度；h为液深；l为液舱长度。

由式(2)可以计算出矩形液舱的一阶和二阶固有频率分别为ω0=6.9008 rad/s、ω1=14.9973 rad/s。

为探究较大激励幅度下多孔挡板对液体晃荡产生的影响，将运动平台激励的振幅设置为A=70 mm，满足恶劣环境时波浪载荷对船舶的动态响应。激励频率ω的范围为[0.40ω0,2.00ω0]，如表1所示。在一阶固有频率附近进行适当的加密处理，以保证数据的准确可靠。每组试验采样时间为256 s，采样频率为128 Hz。

表1 试验外激励频率

1.3 大振幅激励下冲击压力的频率响应

基于大振幅水平激励试验平台开展不同频率下的晃荡试验。图3为无挡板与多孔挡板在70 mm振幅激励下晃荡时冲击压力峰值的频率响应曲线，并与薛米安等[25]在7 mm的小振幅下的结果进行比较。其中横坐标是外激励频率与一阶固有频率的比值，纵坐标是冲击压力的最大值。

(a)无挡板模型

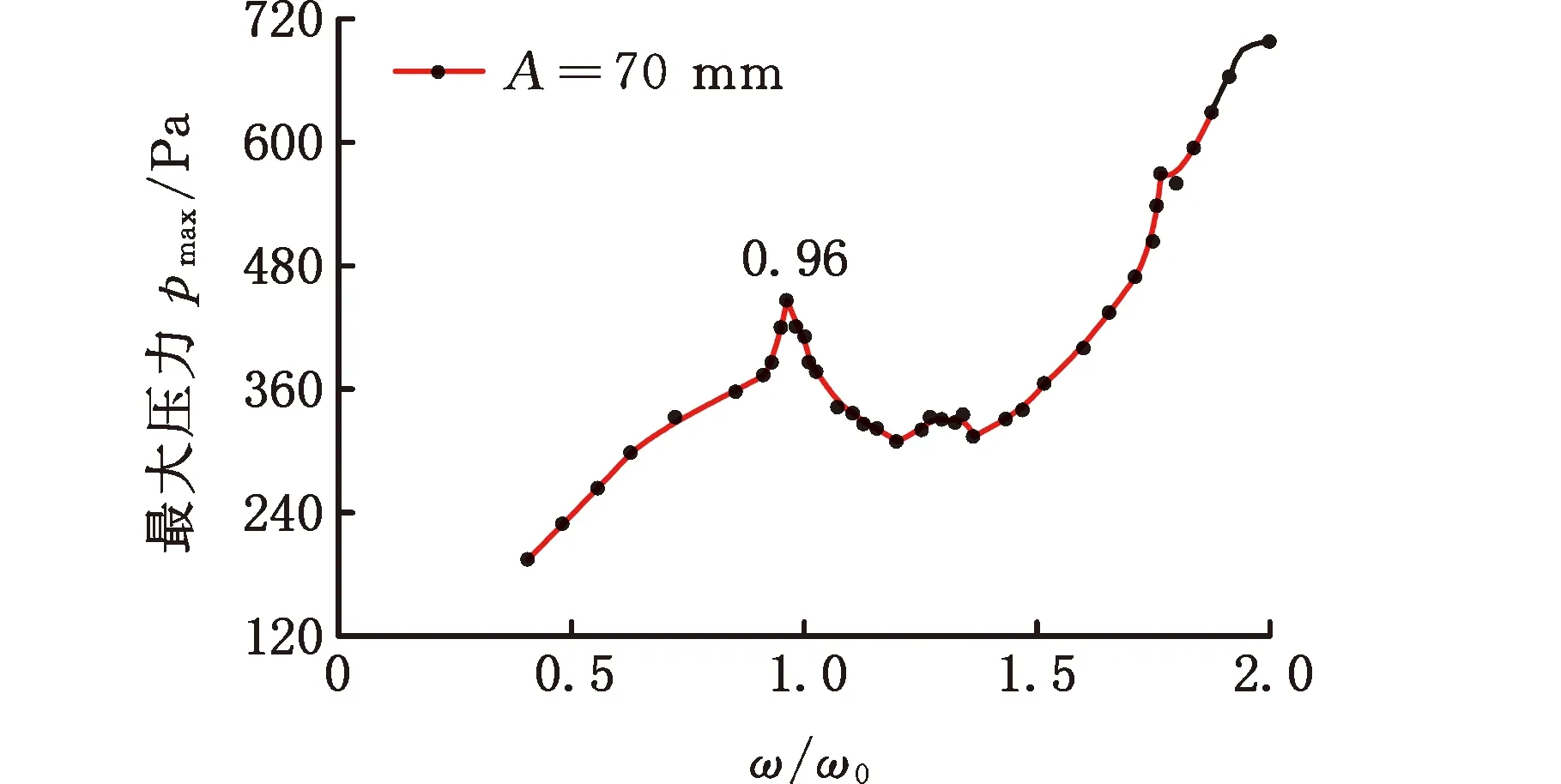
(b)多孔挡板模型图3 最大冲击压力对频率的响应规律

在图3a所示无挡板液舱中，大振幅激励下一阶共振频率发生在0.93ω0，而小振幅激励下一阶共振频率发生在1.06ω0。这里的一阶固有频率ω0忽略波浪的翻卷、破碎以及气泡夹带等强非线性现象，而依据试验得到最大冲击压力的响应频率则包含了波浪破碎等非线性特征的作用。大振幅激励与小振幅激励的最大冲击压力频率响应规律相近，在一阶共振频率处都出现了较大的冲击压力响应，但大振幅激励下响应曲线在大于一阶共振频率后，并未下降到较小值，而是在700 Pa左右浮动，表明非线性晃荡时冲击载荷对频率的响应规律与小幅线性晃荡有区别。当在液舱中加入多孔挡板之后，一阶共振频率处的最大压力迅速减小，且一阶共振频率发生在0.96ω0处，表明液体晃荡的幅度减弱后，一阶共振频率会更加接近液舱的固有频率。结果表明，剧烈晃动引起的非线性液体状态与平稳状态有较大差异，多孔挡板对液体剧烈晃动的抑制过程需要进一步试验研究。

2 冲击压力时域、频域特性

2.1 冲击压力时域特性分析

图4所示为无挡板与多孔挡板模型在激励频率为0.8ω0(接近一阶固有频率)、1.0ω0(一阶固有频率)与1.2ω0(远离一阶固有频率)的压力曲线。当激励频率为0.8ω0时，无挡板模型在0～5 s内冲击压力峰值较高，之后逐渐趋向于稳定状态，稳定后的压力峰值在350 Pa附近；而加入多孔挡板后，压力曲线趋向于平稳，且压力峰值在300 Pa左右波动，与稳定后的无挡板模型压力峰值较为接近。表明在接近一阶固有频率时，液舱中液体本身晃荡幅度较小，多孔挡板对晃荡的抑制效果并不明显。当激励频率为1.0ω0时，无挡板冲击压力曲线的波峰达到799 Pa，波谷位置的压力幅值为-600 Pa(自由液面高度低于液压传感器高度(图5a)，而多孔挡板的压力曲线比较稳定且压力峰值仅为351 Pa，表明该激励频率下液体晃荡的幅度显著减小，多孔挡板抑制晃荡冲击的效果亦更加显著。图5所示为激励频率为1.0ω0时晃动的流场形态，可看出无挡板模型晃荡十分剧烈，出现了液体冲击舱顶的现象，而多孔挡板模型中液体沿液舱壁面爬升的高度较低，并且挡板壁面处也出现了壁面爬升的现象，表明多孔挡板阻碍了液体的剧烈晃荡。

(a)无挡板模型

(b)多孔挡板模型图4 无挡板与多孔挡板在不同激励频率下的压力曲线

(a)无挡板左壁爬升 (b)无挡板右壁爬升

(c)多孔挡板左壁爬升 (d)多孔挡板右壁爬升图5 无挡板和多孔挡板晃荡过程流场形态(ω=1.0ω0)Fig.5 Flow field morphology of without baffle and porousbaffle in sloshing process(ω=1.0ω0)

(a)无挡板左壁爬升 (b)无挡板右壁爬升

当激励频率为1.2ω0时，无挡板压力曲线幅值明显减小，但是出现了双峰现象，且第一个峰值要明显大于第二个峰值。第一个峰值来源于晃荡造成的行进波对舱壁的冲击型压力，伴随着行进波的继续爬升，产生了第一个峰值；随后行进波失去动能，在重力效应的影响下，快速回落的水团撞击自由液面，产生了第二个峰值[25]。相比之下，液舱中加入多孔挡板之后，激励频率的变化对压力曲线特征的影响较小。图6所示为激励频率为1.2ω0时晃动的流场形态，相比于激励频率为1.0ω0，无挡板模型中液体沿壁面爬升的高度明显减小，而多孔挡板模型在两种频率下爬升的高度相近，但激励频率为1.2ω0时

(c)多孔挡板左壁爬升 (d)多孔挡板右壁爬升图6 无挡板和多孔挡板晃荡过程流场形态(ω=1.2ω0)Fig.6 Flow field morphology of without baffle and porous baffle in sloshing process(ω=1.2ω0)

液体撞击多孔挡板后的波浪破碎现象更加明显。以上结果表明，在大振幅激励下，激励频率越靠近一阶共振频率，无挡板模型中液体晃荡幅度越剧烈，但加入多孔挡板之后，激励频率的变化对压力曲线特征的影响较小，始终比较稳定且压力幅值较小，表明多孔挡板抑制液体剧烈晃动的效果显著。表2对冲击压力曲线的峰值与峰宽(从0到峰值再到0的时间)特征进行了统计分析。表2表明，随着激励频率的增大，总会出现峰宽的减小，并且加入多孔挡板也会起到减小峰宽的作用。无挡板模型在激励频率为1.0ω0时，虽然液体晃荡冲击压力峰值高于激励频率为0.8ω0和1.2ω0时的冲击压力峰值，但多孔挡板对压力峰值的降低率也更高。多孔挡板能够减小液体晃荡冲击压力的峰值与峰宽，并且一阶固有频率处压力峰值降低率更显著。

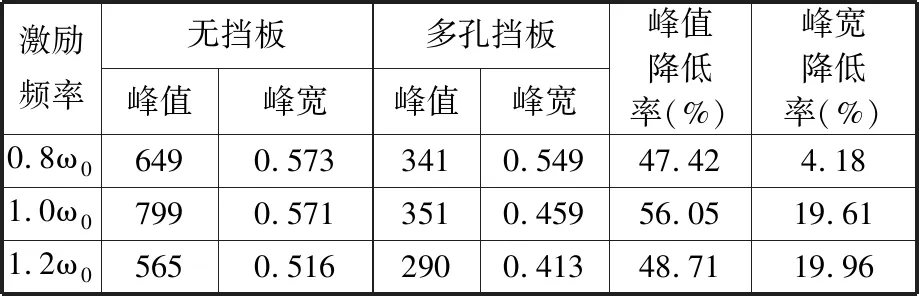
表2 不同激励频率下压力曲线特征

2.2 冲击压力频域特性分析

由2.1节的分析结果可知，当激励频率为1.0ω0时，液体晃荡的幅度较为剧烈，对壁面产生强烈的冲击，因此本节将对该激励频率下的冲击压力信号进行幅频与时频特性分析。

2.2.1幅频特性

冲击压力信号在时域上较难发现明显的特征，采用FFT将时域信号变换到频域，然后提取信号的模态信息，结果如图7所示。由图7可知，液舱中安装多孔挡板对大幅晃荡下冲击压力信号的主要频率成分(简称主频成分)没有影响，主频成分依然是外激励频率和其倍频，其中倍频的能量主要来源于非线性的晃荡波浪相互作用。比较主频成分的冲击压力幅值，多孔挡板模型的主频所对应的压力幅值分别为245 Pa和11 Pa，相对于无挡板模型，压力幅值分别降低了51.48%和93.99%。表明多孔挡板从幅频角度降低液体对壁面冲击压力的有效性。

(a)无挡板模型

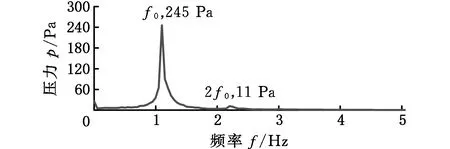
(b)多孔挡板模型图7 冲击压力信号的FFT分析(ω=1.0ω0)Fig.7 FFT analysis of impact pressure signals(ω=1.0ω0)

2.2.2时频特性

(a)无挡板模型

(b)多孔挡板模型图8 冲击压力信号的时频谱(ω=1.0ω0)Fig.8 Time spectrum of impact pressure signals(ω=1.0ω0)

FFT提取信号频谱时，是对该段信号全部时域信息进行整体变换，不具有时间与频率的定位功能。而HHT可以依赖信号本身特征进行自适应分解，得到该段信号的时域和频域联合分布信息。从时频域方面对大振幅激励下的冲击压力信号进行探讨，获得表征冲击压力信号在时间-频率-能量的关系，如图8所示。分析发现，在多孔挡板模型的时频谱中，只存在低频，而无挡板模型除了在1.0 Hz附近的低频之外，在更高频率2.0 Hz附近也存在明显的频率波动。其中低频代表冲击过程中液体的整体运动形态，高频则是代表着晃荡过程的气液混合、波面破碎以及液体飞溅现象。并且，结合图中的能量分布可以看出，在无挡板模型的结果中，频率成分的能量大于600 Pa，而多孔挡板模型的能量仅在300 Pa左右。结果表明，无挡板的冲击压力信号的时频域含有低频和高频成分，而多孔挡板只有低频成分，并且该频率所对应的能量较低。

3 多孔挡板抑浪机理

利用ANSYS-FLUENT软件平台，基于动网格耦合VOF(volume of fluid)的数值模拟方法，对液舱大幅晃荡进行数值模拟。首先将计算区域离散化，用变量的离散分布近似解代替精确解的连续数据。采用二阶迎风格式对控制方程进行离散化，降低数值上的扩散误差。压力-速度耦合求解器采用PISO算法，通过预测—修正—再修正，可以更好地同时满足连续方程和动量方程。单元中心的变量梯度采用更加精确的格林-高斯节点方法；计算面上的压力插值采用可以计算高度旋流的PRESTO方法；界面重构采用几何界面重构方法。液舱模型网格单元尺寸为4 mm，挡板区域局部加密到2 mm，共有2 057 299个网格。主要的控制方程如下:

连续性方程

·U=0

(3)

动量方程

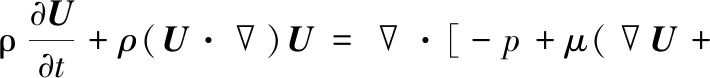
(4)

VOF方法是通过求解流体体积分数α来追踪液相与气相界面(液相与气相的体积分数α分别为1和0)。流体体积分数α输运方程为

(5)

对比相同工况下图9a试验和图9b数值模拟的液面轮廓可知，二者重合度较高，表明该数值模拟方法模拟液体剧烈晃荡的可行性。并且，可发现在液舱中安装多孔挡板后，挡板结构影响了液体剧烈晃荡过程中行进波的传递。高速的行进波撞击多孔挡板，多孔挡板的固体部分阻碍了行进波中大部分液体的流动，同时由于多孔挡板的孔隙之间存在间距，剩余小部分液体被分割成多股射流通过孔隙，急剧降低了行进波传递速度。

(a)试验 (b)数值模拟图9 液体穿过多孔挡板孔隙瞬间

图10a和图10b所示分别为无挡板与多孔挡板模型在同一时刻下的流线和流速。在图10a无挡板模型中，液舱壁面处的流体以较大的流速沿壁面爬升，相比之下，图10b中液舱壁面处的流速和液面高度均较低。观察发现，当液舱向右运动时，多孔挡板的“背风面”产生流线旋转的现象(图10b圈出区域)。这是由于多孔挡板的阻碍作用，导致挡板两侧的流体存在较大的速度梯度，产生涡旋运动。

湍流中涡的强度通过涡量表示，涡量定义为瞬时速度场的旋度，其计算公式为

Ω=×U

(6)

式中，Ω为涡量矢量，涡量反映了流体微团涡旋运动的强度。

Q准则将局部速度梯度张量分解成一个对称张量Sij和一个反对称张量ωij，分别表示流体的变形和旋转部分；Q>0表示旋转占主导部分，认为存在涡旋运动。采用Q准则对液体晃荡过程中的涡结构进行捕捉，定义为

(7)

(a)无挡板流场 (b)多孔挡板流场

(c)多孔挡板涡结构图10 液舱中间切面的流场与涡结构

基于Q准则对t=4.73 s时涡旋运动进行捕捉，结果如图10c所示。红色区域表征Q>0，表示存在涡旋运动，蓝色区域表征Q<0，表示存在变形。图10c中Q>0区域与图10b流线旋转区域一致，表明Q准则表征涡旋运动的有效性。液深为90 mm，图11给出了左侧多孔挡板(1/2高度)壁面区域的涡量，可以看出，仅多孔结构的边缘位置出现较大的涡旋运动，表明液体通过多孔挡板孔隙产生速度梯度，使流体内部形成较大范围的涡旋运动，耗散大幅晃荡时流体中剧烈的能量，抑制流体对液舱壁面的冲击。

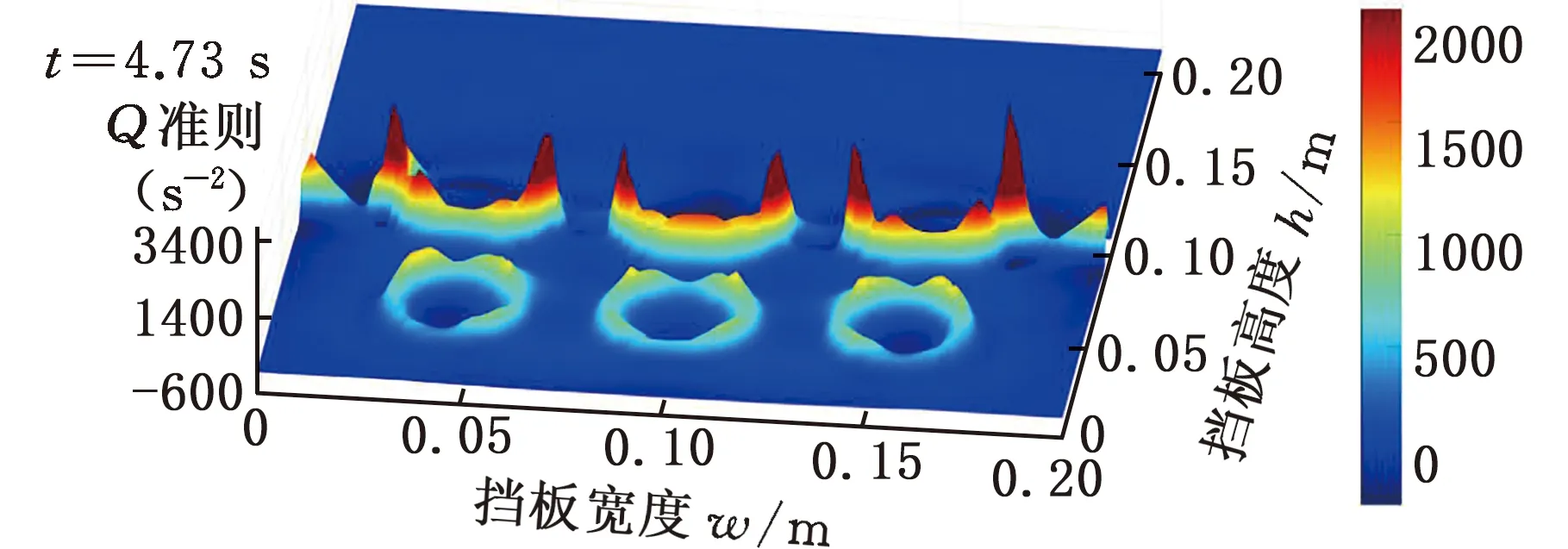
图11 左侧多孔挡板(1/2高度)壁面区域的涡量

结果表明：多孔挡板的固体结构阻碍了行进波中大部分流体运动，剩余小部分流体通过了多孔挡板的孔隙；挡板两侧速度梯度导致孔隙边缘产生耗散能量的涡旋运动，减缓了流体对液舱壁面冲击。

4 结论

(1)构建了大振幅水平激励试验平台，采用试验与数值分析的方法对多孔挡板影响液体晃荡的冲击压力特征进行研究，发现大振幅激励下冲击压力对频率的响应规律与小振幅的结果有区别；波浪翻卷、破碎等非线性特征会导致共振频率偏离固有频率。

(2)多孔挡板能够减小液体晃荡冲击压力的峰值与峰宽，并在一阶固有频率处压力峰值降低率更显著。

(3)多孔挡板不改变幅频中的主频成分，但主频的压力幅值明显减小；多孔挡板的时频谱仅有低频成分，并且每个时刻的频率所对应的能量较小。

(4)挡板固体结构和孔隙的涡旋减缓了液体的剧烈晃荡。穿过孔隙的液体产生耗散能量的涡旋运动，但孔隙越大，挡板结构阻碍行进波效果越差；小孔隙会影响液体的流动畅通，需合理权衡。