往复运动速度规划算法对曲线磨削的影响研究
谢朝珑 许黎明 王昆梓 周 超 赵 达
上海交通大学机械与动力工程学院,上海,200240
0 引言
往复加工形式常见于磨削、刨削等金属切削中,加工过程往往呈现加速度大和断续加工的特点,所带来的刚性冲击和柔性冲击会直接影响加工过程的平稳性,从而影响产品的加工质量、能源效率乃至机床的寿命。曲线磨削作为一种精密加工方式,可加工复杂轮廓曲线,加工面就是以曲线为加工母线的轮廓曲面,轮廓曲面就是通过圆弧砂轮的上下往复运动(或称冲程运动)叠加水平插补运动形成的包络面。传统的光学曲线磨削通常采用曲柄滑块机构来实现砂轮的冲程运动,冲程速度的变化规律主要由硬件决定。随着曲线加工方式的不断改进,砂轮的往复运动从传统的机构实现发展到伺服驱动实现,为运动速度的柔性规划提供了条件,但目前主要还是以梯形和S形速度规划为主,因此,亟需针对冲程运动要求研究优化其速度规划算法及其对加工过程的影响,这对提高加工过程平稳性、保证产品加工质量和降低能源消耗均具有非常重要的意义。
目前,相关研究多集中于数控加工进给速度的规划算法,常见的有直线加减速控制方法、指数加减速控制方法和S形加减速控制方法[1-2]。直线加减速控制方法与指数加减速控制方法在加减速阶段存在加速度突变,由此产生的惯性力瞬变会激励机床产生振动,影响加工质量。为此,很多学者研究了保证加速度乃至加加速度(急动度)连续的加减速规划方法,主要包括提高速度规划多项表达式的阶数、利用无限可导的函数等。李志杰等[3]提出了一种急动度无突变且起止端连续的加减速曲线控制方法,加速度曲线由三角函数与直线组成,与纯三角函数相比曲线可控性更强。ZHANG等[4]在数控加工中利用B样条曲线对刀具轨迹进行了光滑处理,基于线性规划算法提出以进给运动学参数为多约束条件的连续几何轨迹时间优化方法,提高了轮廓加工性能和加工效率。HUANG等[5]在五轴数控加工过程中,利用分段多项式轮廓分别规划直线轨迹和角轨迹,并提出一种时间同步的双向扫描方法,使速度整体连续,与传统方法相比,该方法减小了轮廓加工误差。吴继春等[6]根据加工路径的几何形状特性对加工路径进行细分,在连续急动度的基础上对每段路径进行速度规划,使其能够满足加工过程中机床的动态特性要求。JAHANPOUR等[7]提出了一种自适应急动度限制的非均匀有理 B 样条曲线插值方法,仿真结果证明插值算法能够提供平滑的进给速度过渡,并满足整体加工时间的要求。WANG等[8]提出了一种基于预插值和前瞻性插值的三角函数速度规划算法,实现了速度、加速度、加加速度的平滑控制,减小了弦误差,实现了高质量的数控加工。
轨迹规划是机械手轨迹控制的基础,其性能对机械手工作效率、运动平稳性等具有重要影响。贾山等[9]对可移动着陆器腿足机构各关节空间内的运动轨迹进行了以时间-急动度最优为目标的优化规划,建立了轨迹优化模型,通过多种群遗传算法对模型进行搜索求解,减小了着陆器腿足机构运动过程中的冲击和振动。朱世强等[10]以机械手作业效率为优化目标,采用7次B样条曲线插值方法构造了急动度连续的关节轨迹,并通过求解最优时间节点,规划出了时间最优脉动连续轨迹,使机械手能快速平稳地跟踪空间任意指定轨迹。FANG 等[11]利用分段S形Logistic函数建立了一种急动度规划,用以满足机器人高速和精密操作的要求,生成的轨迹在给定的速度、加速度和急动度条件下连续可微,这种S曲线模型比传统函数模型具有更高的效率,同时避免了传统高次多项式模型的复杂性。CONSTANTINESCU 等[12]提出了机械手路径约束下运动平滑和时间优化的轨迹规划方法,将驱动器扭矩作为限制条件,将急动度作为被控输入量,将时间作为优化目标,设计出了一种时间优化的平滑轨迹。BEAREE等[13]提出了一种通过急动度限制的轨迹规划抑制时变振动的方法,并将其应用于三轴笛卡儿机械手,有效减小了机械手工作中的振动幅度,并在一定程度上提高了作业效率。
基于轨迹规划的能耗研究相对较少,ZHOU等[14]提出了一种节能型轨迹规划方法,用于机器人高速铣削复杂曲面,该方法建立了机器人加工系统的能量特性模型和具有复杂约束条件的轨迹规划模型,结果表明该方法显著降低了加工能耗,并提高了轨迹规划的效率,该方法有待集成进入制造系统。
上述研究结果在实现加速度、加加速度等运动学参数的平滑控制方面对往复加工运动的速度规划具有借鉴意义,但往复加工具有往复频率高、切削断续的特点,其往复速度规划不同于常规数控进给加减速规划和机械手轨迹规划,而且对于曲线磨削来说,冲程运动的速度规划和加工过程平稳性、加工表面质量和加工能耗之间的关系还有待深入研究。为此,本文首先讨论了冲程运动速度规划的设计方法,然后研究了优化急动度空间分布的速度规划算法,并对不同规划的运动学性能进行了比较,分析了不同速度规划对加工过程中磨削力的平稳性、工作能耗和加工表面粗糙度的影响。最后,综合理论和实验研究,得出磨削冲程速度规划的优化结果。
1 冲程运动速度规划算法和仿真分析
1.1 传统运动规划
传统速度规划包括梯形速度规划、S形速度规划、正弦速度规划等。首先,在无匀速段条件下,速度由匀加速和匀减速段组成,设时间变量为t,冲程运动的单程时间为T,往复频率为f,单程距离为s。利用MATLAB进行仿真,同时设f=1.25 Hz,s=40 mm,可以得到梯形速度规划、S形速度规划以及正弦速度规划的单程速度规划的速度v,加速度a以及急动度j,仿真结果如图1a所示。在有匀速段条件下,设匀速段时间为T/2,梯形速度规划以及S形速度规划仿真结果如图1b所示。

(a)无匀速段

(b)有匀速段图1 传统冲程运动的速度规划
可见,梯形规划的加速度在启动、停止、匀速前后节点均有加速度的跳变,应用于冲程运动,急动度不连续,且在无匀速段的行程中点发生突变,存在较大的柔性冲击。S形规划的急动度有限,与梯形速度规划相比,避免了较大的冲击,但急动度随时间变化不连续,在无匀速段的行程中点出现急动度跳变,会对系统产生一定的柔性冲击。正弦速度规划相对梯形速度规划与S形速度规划更为平滑,同时急动度连续可导,但无法实现匀速段加工,同时在行程中点的急动度最大。
传统曲线磨床的砂轮往复运动由曲柄滑块机构实现,运动曲线近似于正弦规划,可归为一类,但受结构所限,其运动形式固定,运动过程存在一定的不对称性。
1.2 改进急动度空间分布的运动规划
1.2.1正弦叠加梯形速度规划(Ⅰ型速度规划)
该运动规划定义为将梯形速度规划中的加速度叠加一个周期的正弦波动,消除梯形速度规划中加速度与急动度的突变,这样不仅可以实现急动度连续,而且使冲程半周期里行程起始点、中点与终止点的急动度都为0。加速度函数a(t)可表示为
(1)
其中,a1、a2分别为运动过程中的加速度与减速度幅值,t1、t2分别为加速时间与减速时间。在给定f=1.25 Hz、s=40 mm时,利用MATLAB对运动过程进行仿真,无匀速段与有匀速段(时长为T/2)的单程运动规划仿真结果分别如图2a和图2b所示。结果表明,急动度连续,运动过程平滑,行程中点的急动度为0。由于起点、终点加速度均为0,也适合单次往复运动使用。

(a)无匀速段
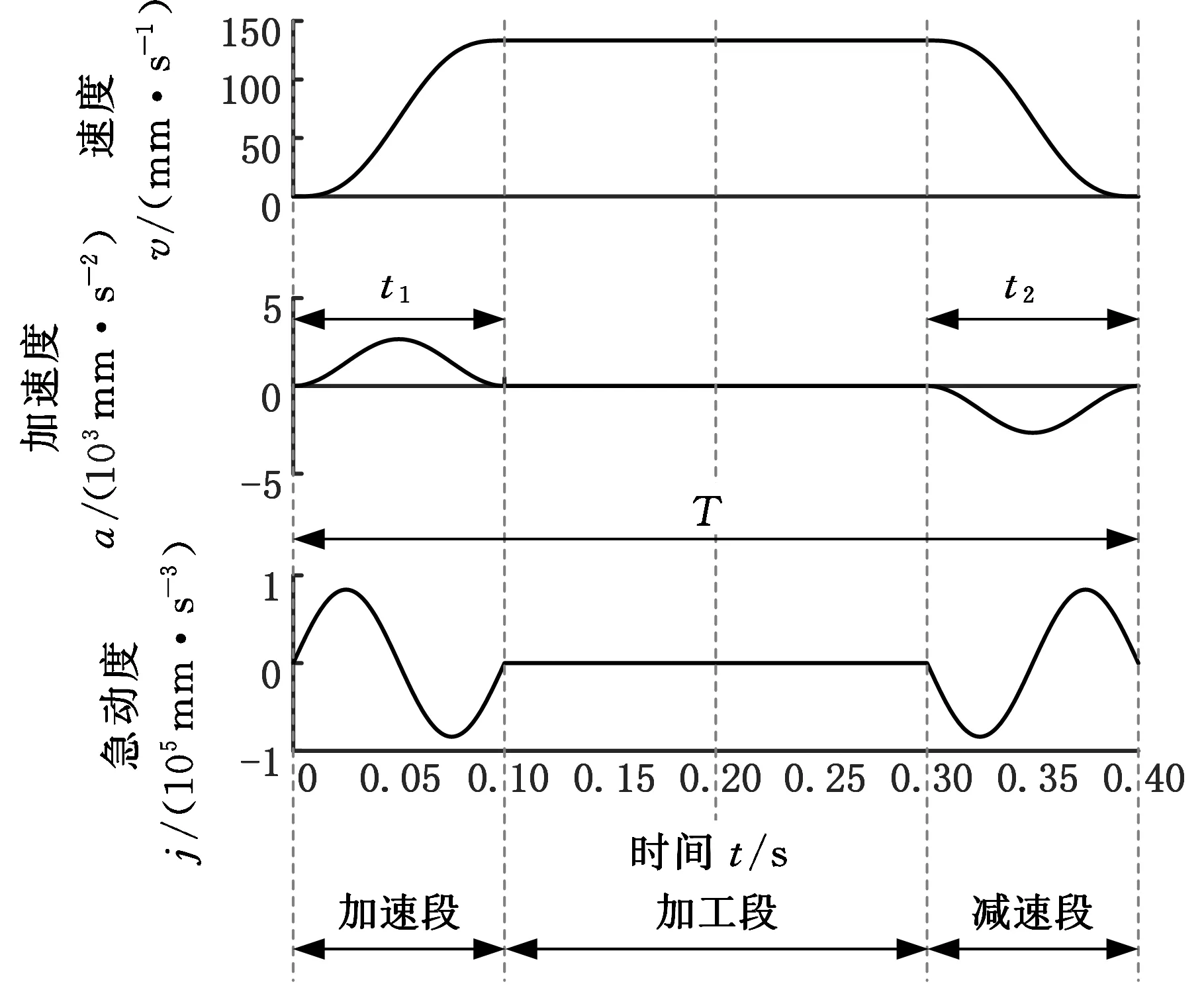
(b)有匀速段图2 Ⅰ型速度规划
1.2.2加速度前瞻速度规划(Ⅱ型速度规划)
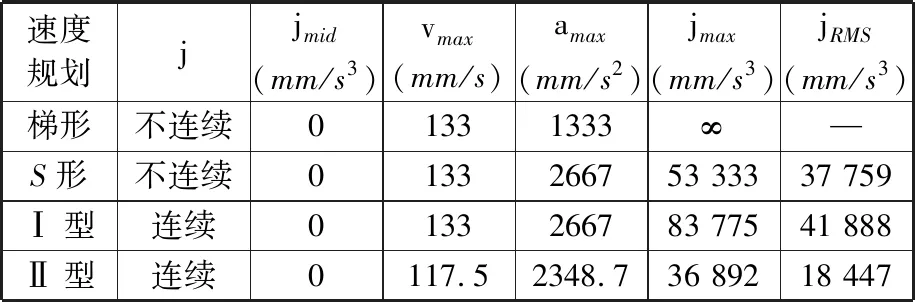
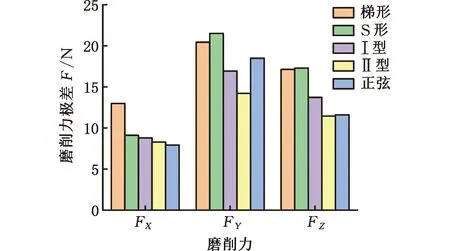
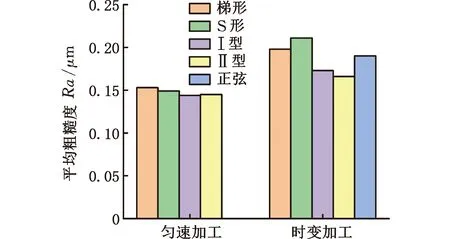
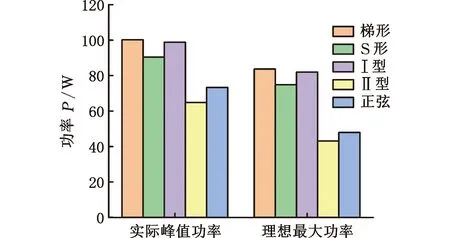
该规划同时改进急动度和加速度的空间分布,设计目标为:①保证行程中点的急动度最小;②磨削冲程两端以最大加速度过渡,提高运动效率,降低规划的最大急动度;③可实现加工段的匀速。当有匀速段时,单程运动可分为三段,即减加速段(t 先设计减加速段:由于在端点处加速度是极大值点,因此此时急动度为零。同时,要求急动度在行程中点即t=tm(无匀速段)时为零,建立急动度函数: j(t)=-jmaxsin(πt/tm) (2) 式中,jmax为急动度的最大值。 设a在t=0处有最大值,在t=tm处为0,由此可推导出运动学参数轨迹方程如下: (3) 由式(3)可计算最大加速度和最大速度分别为 (4) 同样,加减速段可根据减加速段进行对称设计。行程给定后,jmax与tm的关系就唯一确定了。下面讨论无匀速段和带匀速段两种模式的运动规划: (1)无匀速段模式。根据对称性,往复运动周期的急动度函数为 (5) 同样,设f=1.25 Hz,s=40 mm,由式(2)、 式(3)、 式(5),仿真得到运动曲线如图3a所示,行程中点的急动度为零,减小了加工中的柔性冲击。 (2)有匀速段模式。行程中间带匀速加工段,单程急动度函数为 (6) 单程加速度函数为 a(t)= (7) 单程速度函数为 v(t)= (8) 单程位移函数为 s(t)= (9) 在无匀速加工模式中的T/2及3T/2处插入两个匀速段,不影响原有的连续性,给出匀速加工段长度后即唯一确定了速度规划。设往复频率和行程同上,单程匀速段时长为T/2,仿真结果如图3b所示,整体急动度连续,加工段急动度为零。 (a)无匀速段 (b)有匀速段图3 Ⅱ型速度规划 在往复频率f=1.25 Hz、单程s=40 mm且无匀速段时,不同速度规划的运动学性能仿真结果见表1。表中,jmid代表行程中点的急动度。结果表明,所设计的Ⅰ型和Ⅱ型速度规划不仅急动度连续,而且行程中点的急动度均为0。虽然正弦速度规划的最大急动度也较小,但其最大急动度出现在行程中点,且最大速度大于Ⅱ型规划最大速度,对能耗也会产生影响。梯形和S形规划的急动度均不连续,且最大值同样分布在行程中点。 表1 无匀速段不同速度规划的运动学性能比较 同样,有匀速段条件下,匀速段时长占行程时长的一半,其他参数不变,比较不同速度规划的运动学性能,见表2。结果表明,所设计的速度规划均在急动度上连续,其中Ⅱ型规划的最大速度、最大加速度与最大急动度均最小。与无匀速段规划相比,带匀速段规划的最大加速度和最大急动度均呈大幅上升。 表2 有匀速段不同速度规划的运动学性能比较 上下往复运动系统在上行过程中需要克服重力做功,在不考虑摩擦及阻尼等能量损耗的情况下,不同速度规划的理想功率P(t)为 (10) 在一个周期T内的能耗为 (11) 式中,mgw为砂轮架质量;g为重力加速度;h为丝杠导程;Jmz为驱动电机输出轴转动惯量。 在往复频率f=1.25 Hz、单程s=40 mm且无匀速段条件下,不同速度规划的理论最大功率如表3所示。梯形速度规划的峰值功率最大,Ⅰ型速度规划次之,正弦速度规划的峰值功率较小,而Ⅱ型速度规划峰值功率最小,说明它对电机的驱动能力要求最小。 表3 不同速度规划理论最大功率 实验主要研究不同运动规划对砂轮架运动的平稳性、磨削力平稳性和零件加工表面粗糙度的影响。实验平台为自主开发的曲线磨削样机,结构原理如图4所示,设备由机械系统、运动控制系统及视觉系统构成。砂轮架往复运动由Z轴伺服驱动实现,砂轮旋转由电主轴驱动。砂轮的平面运动由U、V伺服轴控制。工件安装在工作台上,由X轴、Y轴直线电机驱动实现平面运动。视觉系统用来获取加工曲线的轮廓图像,在线监控加工轮廓误差。 图4 曲线磨削试验样机结构图 运动控制器采用Trio公司的MC4N-ECAT,Z轴驱动采用松下伺服位置控制模式,砂轮架冲程运动的速度规划通过数控系统的电子凸轮功能实现,速度规划轨迹的理论与实际偏差小于0.3%。实验采用薄型双斜圆弧铬刚玉砂轮,型号为P150×6×32PA120k8V35,砂轮刀尖为圆弧,轮廓如图4所示。试件材料为高速钢,硬度为67HRC,厚度为16 mm,两侧设计了均匀分布的凸台,凸台的宽度为6 mm,间距为6 mm,如图5所示。每个凸台可用作一次加工实验,上面标签代表不同组别,这样可以减少工件装拆及对刀次数。 图5 实验加工工件 测力仪固定在工作台上,修整轮与工件安装在测力仪上,如图6所示。工件坐标系为O1XYZ,砂轮坐标系为O2UVZ,力坐标系为O1FXFYFZ,FX、FY、FZ分别代表轴向、法向和切向磨削力。 图6 速度规划加工实验装置图 实验流程设计如下: (1)砂轮修整。每次加工前修整砂轮,砂轮进给速度为1.5 mm/s,进给量为0.015 mm。 (2)修整完毕后移动砂轮至加工位置,按照设定好的砂轮架的速度规划,对实验指定凸台表面进行初次加工,设置磨削深度为0.01mm,进给速度为0.02 mm/s,往复行程为40 mm,往复频率为1.25 Hz。 (3)二次加工同一凸台表面,加工参数不变,加工中采集磨削力等过程信号。 (4)改变冲程速度规划类型,重复步骤(1)~步骤(3),加工下一凸台。工件所有凸台表面加工完毕后,进入步骤(5)。 (5)将工件取下测量所有凸台表面粗糙度。 往复曲线磨削加工是一种需要持续轴向进给的点磨削,实验中在加工稳定状态连续采集300 s的磨削力信号,将原始磨削力信号经过高通滤波处理,计算出三个方向状态信号的极差值与均方根值,以此来衡量磨削力的平稳性。在时变和均匀条件下,速度规划对磨削力平稳性的影响结果分别如表4和表5所示,图7描绘了速度规划对磨削力极差值的影响。 表4 冲程速度时变时磨削力统计结果 表5 冲程速度均匀时磨削力统计结果 (a)时变加工 (b)匀速加工图7 不同速度规划下的磨削力极差值 分析可见,在加工段速度时变条件下,梯形和S形速度规划的磨削力极差大,平稳性相对较差。正弦和Ⅰ型速度规划的磨削力平稳性相对较好,而Ⅱ型速度规划下磨削力最小,平稳性也最好。在加工段匀速条件下,相对于时变条件,梯形规划尤其是S形规划的磨削力平稳性得到一定的提高,而Ⅱ型速度规划下的切削力总体幅值和波动依然最小。 总体来看,曲线冲程磨削时, Ⅱ型速度规划的磨削力最小,平稳性也最佳,其切向力和法向力波动较梯形规划减小了30%以上。Ⅰ型规划与正弦速度规划的磨削力平稳性比较接近,而梯形速度规划的磨削力及其波动均最大。 基于第2节介绍的实验条件和方法,完成磨削试验后,测量各个凸台加工表面粗糙度的分布情况,工件表面如图8所示。可以看出工件外观质量好,表面光滑,呈现一定的反光效果。粗糙度的测点布置如图9所示,其中图9a为轴向粗糙度测点布置图,7个均布测点的测量方向垂直于冲程运动方向;图9b为冲程运动方向(切向)粗糙度测点布置图。在加工段冲程速度时变和均匀条件下,分别计算不同速度规划对应的加工表面轴向粗糙度平均值、标准差和极差值,重复三次实验,统计结果如表6所示,不同速度规划的轴向表面粗糙度平均值分布如图10a所示。 图8 加工后工件表面图 (a)轴向粗糙度测点 (b)切向粗糙度测点图9 粗糙度测点分布 表6 不同速度规划对应的轴向粗糙度统计值 结果表明,匀速加工的轴向表面粗糙度要小于时变加工的轴向表面粗糙度,同时各速度规划下轴向粗糙度均值差别较小,极差也基本一致。在时变加工条件下,Ⅱ型、Ⅰ型规划和正弦规划对应的轴向粗糙度极差最小,约为梯形和S形的50%,而Ⅱ型和Ⅰ型规划粗糙度平均值最小,约比梯形和S形规划粗糙度平均值减小了20%,反映了粗糙度大小和急动度的空间分布、幅值均相关,切削过程中优化急动度空间分布、抑制急动度均利于加工表面质量。 同样,在加工段冲程速度时变和时不变条件下,分别计算不同速度规划对应的加工表面切向粗糙度平均值、标准差和极差,重复三次实验,统计结果如表7所示,切向粗糙度平均值分布如图10b所示。结果表明,不论冲程速度是均匀还是时变,Ⅰ型和Ⅱ型规划的平均切向粗糙度均较小, 在匀速条件下,Ⅰ型和Ⅱ型规划的平均切向粗糙度约比梯形和S形速度规划减小20%;在时变条件下,Ⅱ型规划的切向粗糙度最小,约比梯形规划小30%,比正弦规划也减小了20%以上。因此,急动度的空间分布和幅值对切向粗糙度的影响相较轴向粗糙度更大。 表7 不同速度规划对应的切向粗糙度统计值 (a)轴向 (b)切向图10 不同速度规划下加工表面平均粗糙度 总体来看,不同速度规划对切向粗糙度的影响要大于对轴向粗糙度的影响,Ⅱ型规划条件下的加工表面粗糙度最小,这一方面是由于空间急动度分布合理且幅值较小,减小了对加工表面的冲击,另一方面,即使是时变加工条件下,Ⅱ型规划相比其他速度规划在行程的中间最接近匀速,因此时变加工和匀速加工的表面粗糙度结果比较一致。 实验平台见第2节,实验条件与1.5节中理论功率的计算条件一致,采用中创智合型号为ZH-40074的功率采集器实时采集驱动电机的功率,采样周期为40 ms,分析得出不同速度规划对应的实际峰值功率,并与式(10)算得的理论功率进行比较,结果如图11所示。 图11 不同速度规划下的电机能耗比较 由结果分析可见,梯形速度规划的驱动实际峰值功率最大,而Ⅱ型速度规划的实际峰值功率最小,与梯形速度规划相比,功率要求降低了35%。在不同速度规划条件下,实验所测得的冲程运动峰值功率要大于理论功率但趋势一致,这是由于实际工况存在各种阻尼、摩擦等能量损耗,以及理论计算未考虑驱动器本身消耗功率。实验和理论结果都表明,提高运动过程的平稳性,以及优化加速度空间分布即在冲程两端实现最大加速度过渡,均有利于降低工作能耗和电机驱动功率需求。 (1)往复运动速度规划影响运动过程平稳性。梯形速度规划的磨削力及其波动性最大,正弦速度规划的磨削力平稳性与S形规划接近。Ⅱ型规划优化了急动度和加速度的空间分布,降低了最大急动度,磨削力平稳性最好,相比梯形速度规划,其切向力与法向力波动减小了30%以上。 (2)通过降低往复运动急动度的大小和改进急动度的空间分布,可以降低柔性冲击对加工表面质量的影响。不同速度规划对切向粗糙度的影响要大于对轴向粗糙度的影响,Ⅱ型规划条件下的加工表面粗糙度最小,比梯形规划减小约25%。 (3)冲程加工区匀速条件有助于提高梯形和S形速度规划下的磨削力平稳性,减小轴向表面粗糙度,但同时也增大了整个运动过程的最大急动度。 (4)速度规划对电机驱动能耗有较大影响,减小急动度、改进加速度空间布局有利于降低冲程运动工作能耗。梯形、S形和Ⅰ型规划的能耗较大,正弦速度规划的能耗较小,而Ⅱ型规划的能耗最小,与梯形规划相比,能耗降低约35%。
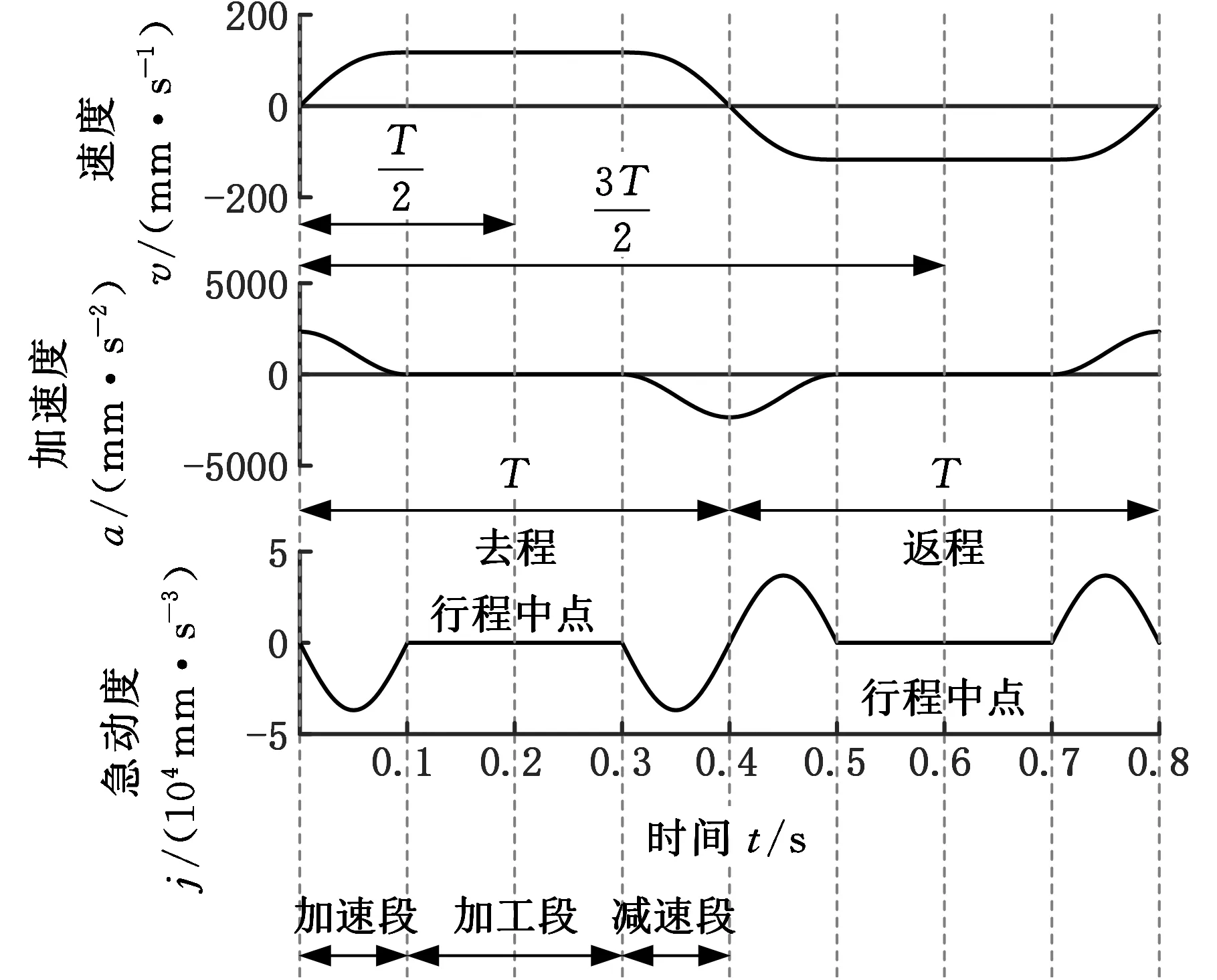
1.3 不同速度规划的性能比较

1.4 不同速度规划功耗分析

2 速度规划对磨削力平稳性的影响
2.1 实验条件和方法



2.2 实验结果与分析



3 速度规划对加工表面粗糙度的影响





4 速度规划对加工能耗的影响实验
5 结论

