一种高精度的机器人手眼标定算法*
胡 为,刘 冲,傅 莉,陈新禹
(1.沈阳航空航天大学航空航天工程学部,沈阳 110136;2.沈阳航空航天大学自动化学院,沈阳 110136)
0 引言
排爆机器人在军事、反恐等领域具有重要的作用价值,该类机器人往往在机械手上安装一台相机用来对可疑物进行观察,并为机械手进行定位。相机与机械手的位置转换关系直接影响机器人的性能,因此,机器人手眼标定的研究具有重要意义。
本文以军用排爆机器人为研究对象,此类机器人将相机固定安装于其机械手末端用以观察可疑物,所构成的手眼系统为系统[1]。通过研究可知,该类手眼系统手眼标定的求解过程就是求解齐次矩阵方程的过程。目前来看求解该方程的方法主要分为两大类:线性方法和非线性方法。其中线性方法为:
传统两步法[2-3]:将旋转矩阵和平移向量进行解耦,该方法需要已知摄像机的内部参数。该算法的缺点是旋转矩阵正交化后再求平移部分,而平移解不再满足手眼矩阵。
共同标定法:同时进行摄像机标定和手眼标定。但是该方法忽略了摄像机的畸变,系统的精度将无法保证。例如Ma[4]提出的无标定物的主动视觉算法,就是通过机械手末端平台带动摄像机运动获取数据参数,利用极点建立约束方程组,求出摄像机的内部参数以及手眼标定矩阵。
数学法[5-6]:通过使用特殊的数学工具如四元数、矩阵直积、拉直运算等数学工具来求解手眼关系。该方法的优点就是不用对旋转平移进行解耦,相对两步法精度要高、鲁棒性强等优点。又如另外一种算法是利用直积将手眼矩阵转换成线性方程组的形式,但是在求解手眼矩阵过程中将会舍去一个方程,使得该算法在测量噪声明显的情况下存在不稳定的情况[7-9];
运动限制法:该算法就是限制机器人做相对正交与平移的运动来实现求解手眼矩阵的目的。在实现方面相对比较困难,需要机器人本身的运动精度高且重复精度也高,同时可以实现一些特殊运动才能采用该方法[10-13]。
非线性方法[14]:Ruda采用数学工具四元数求出初值,然后利用非线性优化得出最终解。王君臣提出一种基于最大似然估计的非线性最优手眼标定算法等[15]。由于本类方法要求较高,实现相对复杂、实用性相对较弱的特点,很少引起学者的注意,在实际应用中并不多见。
鉴于上文提出的线性方法以及非线性方法存在的不足之处,本文提出了一种基于矩阵直积的手眼标定改进算法,该算法可以实现一步化求解、避免已有算法存在的误差传递等问题。本算法将对求取的旋转矩阵进行正交单位化处理从而消除外部噪声的干扰。实验结果表明:改进算法较另外两种现有算法有着更强的鲁棒性和更小的标定误差,满足工程需求,应用广泛。
1 手眼标定传统算法
在eye-in-hand系统中摄像机固定在机械手平台上,跟随机器人一起运动。图1是平台移动前后各个坐标系相对位置关系图。
Cobj是物体坐标系,Cc1、Cc2是摄像机运动前后对应的坐标系,Ce1、Ce2是机械手平台运动前后对应的坐标系,摄像机外参数标定可以求得摄像机坐标系与物体坐标系之间的关系,用Ra、ta表示。摄像机坐标系与机器手平台坐标系之间的关系用t、R表示,即CX=XD中的X。求取X的过程就是机器人手眼标定的过程。图1中的相对位置关系A、B、C、D、X都是4×4齐次矩阵,如:
将CX=XD方程中的各4×4矩阵分别用相应的旋转矩阵以及平移向量写出,并展开得到式(1):
为确保式(1)的解唯一则至少需要两组数据,所以将式(1)进行两次变换处理得到式(2):
2 基于矩阵直积的手眼标定改进算法
本节将介绍基于矩阵直积的手眼标定算法及其改进算法,该类方法将借用矩阵直积和矩阵的特征向量等数学工具对式(1)进行变换求解。
2.1 矩阵直积与线性算子
为了对手眼矩阵进行线性化,将采用矩阵直积以及线性算子对式(2)进行变换求解。如果存在m×n矩阵A和p×q矩阵B:
则A和B的直积A⊗B为mp×nq矩阵:
首先定义线性算子vec并且利用线性算子将矩阵进行拉直运算,即将矩阵A的元素以长为mn的列向量表示:
设A是m×n的矩阵,B是n×n的矩阵,X是m×n的矩阵,由矩阵直积和线性算子vec的定义可知:
当A或B是单位矩阵时,有:
设a和b为常数,则有:
2.2 Moore-penrose逆
且通解为:
由式(8)可知,如果线性方程组Ax=b有解,则当且仅当A+A=I。在实际问题中,需求出线性方程组的无穷多个解中范数最小的解,即,称x0为线性方程组Ax=b的极小范数解。
2.3 基于矩阵直积手眼标定算法
用矩阵直积和线性算子vec对式(2)进行的变换求解可得到式(11)、式(12)。
根据式(11)可知,该式系数矩阵存在特征值为零的特征向量,该向量与齐次方程的解相差一个比例因子。令特征值零所对应的特征向量为γ(γ是9×1的列矩阵),比例因子为常量β,将特征向量与比例因子引入式(12)中,vec(R)、t所对应的系数如式(13)所示。
为使手眼标定线性化,所以将式(11)、式(12)进行线性化,如式(14)所示。
从以上两种算法可知,现有矩阵直积手眼标定算法与传统两步法存在相似之处。在一定意义上都是两步法,所以仍将产生误差传递,从而导致手眼标定精度降低。
2.4 基于矩阵直积的改进算法
接下来将提出手眼标定改进算法,利用矩阵直积和线性算子vec对式(1)进行变换求解。如式(15)所示:
为确保手眼矩阵解的唯一性则至少需要旋转轴做两组不平行的运动,因此,在做两次运动的过程中将会得到两个形如式(15)的两个等式。根据得到的两组方程式分别进行联合:
针对式(16)、式(17)作如下变换,本处变化将不同于一般的矩阵直积,同时也是本改进算法的特点:
式(11)~ 式(18)中 o9×3为 9×3的全零矩阵、o9是9×1的全零矩阵、I3为3×3的单位矩阵。
式(18)是形如Ax=b的方程组,根据矛盾方程组的性质,该方程组左边的系数矩阵为不可逆矩阵,在求解该矛盾方程组的解时将用到广义逆的思想。所以需要求取方程组的极小范数最小二乘解,则该方程组的极小范数最小二乘解X就等于A+b。将旋转矩阵与平移向量进行耦合,将会在计算过程中减少系统噪声带来的误差影响。对极小范数最小二乘解进行重排,将得到手眼标定矩阵中的旋转矩阵以及平移向量。最后对旋转矩阵进行斯密特正交单位化处理,标定结果满足标准正交化。
3 仿真实验结果及数据分析
实验平台主要由:MOTOMAN机器人、机器人控制器、CM3-U3-13Y3M-CS工业相机、棋盘格标定靶、一台计算机等组成。如图2所示。
3.1 实验数据
在内部参数已知的情况下,求出摄像机两次运动所拍摄图片的3个相应外部参数。图3所示为摄像机运动两次在3个不同位置点拍摄的靶标图像,根据该组图像求出相应的摄像机外部参数和机械手平台在该处的位置与姿态。
通过实验可知,图 3 中(a)、(b)、(c)3 个位置点所对应的机械手末端的位置和姿态信息分别是:
pos0、pos1以及pos2位置姿态信息的矩阵形式可通过旋转角度与旋转矩阵之间的变换关系求得,如式(22)~式(25)所示。
式(22)~ 式(24)中 q、w、r分别表示 pos0、pos1以及pos2中各旋转轴的旋转弧度,Rx、Ry以及Rz代表笛卡尔空间各旋转轴的旋转矩阵,R代表旋转向量所对应的旋转矩阵。根据摄像机在位置点(a)、(b)以及(c)处所拍摄3张图片信息,可利用摄像机标定来求得外部参数。
由图3中3张图片所对应的外部参数以及机械手姿态信息进行手眼标定。根据传统两步法求出的未正交化处理的手眼矩阵Xtwo-step以及正交单位化处理之后的机器人手眼矩阵Xtwo-step1,如式(26)、式(27)所示。
同理,基于矩阵直积算法求取的未正交化处理机器人手眼矩阵为Xkronecker以及正交单位化的手眼矩阵Xkronecker1。本文提出的改进算法所对应的未正交化手眼矩阵与正交单位化之后的手眼矩阵分别为Xchange、Xchange1,如式(28)~ 式(31)所示。
在下节将针对本组实验数据以及其余13组数据进行误差分析,根据分析结果来验证基于矩阵直积改进算法的标定精度。
3.2 误差分析
本节将根据实验数据进行标定精度分析并采用范数来检验重复误差,即将3种算法求取的手眼矩阵代入进行误差分析。3种算法的误差比较如表1、表2所示。

表1 第1组未正交化手眼矩阵误差分析

表2 第1组正交单位化手眼矩阵误差分析
表1 中 Xtwo-step、Xkronecker、Xchange分别代表两步法、矩阵直积法以及改进算法的手眼矩阵未正交化时的误差。Xtwo-step1、Xkronecker1、Xchange1分别是对应的3种算法手眼矩阵正交单位化之后的误差。通过表1、表2可知,基于矩阵直积改进算法同现有的另外两种算法相较而言标定精度最高。为准确验证改进算法的标定精度,本节将给出多组实验结果并作分析。
为保证求解的唯一性则需要机器人做两次平台运动,从而存在两组摄像机坐标系以及机器人运动平台坐标系的相对位置关系,所以在图4、图5中都分别会有两组误差分析图。图4中(a)、(b)是手眼矩阵中的旋转矩阵未正交化的误差分析图。
通过图4可知,传统两步法和一般性矩阵直积手眼标定算法鲁棒性较差。未对手眼矩阵中的旋转矩阵正交之前,改进算法表现出很高的鲁棒性且误差结果趋近于零。对手眼矩阵进行正交单位化处理并加以误差分析,如图5所示。
图5中基于矩阵直积算法表现出极不稳定的状态,其次是传统的两步法。结合图4、图5可知,未对手眼标定结果归一化之前改进算法的标定精度非常高且接近于零。在正交单位化之后,改进算法的标定误差结果依然是最理想且满足手眼标定精度要求。下页表3将给出更加直观的平均误差的分析数据,标定误差结果如表3所示。
表3中Xerror、X正交单位化error分别表示手眼矩阵中的旋转矩阵未进行正交化和正交单位化后的平均误差。通过表3中的平均误差分析可知,改进的机器人手眼标定算法误差最小且精度最高。
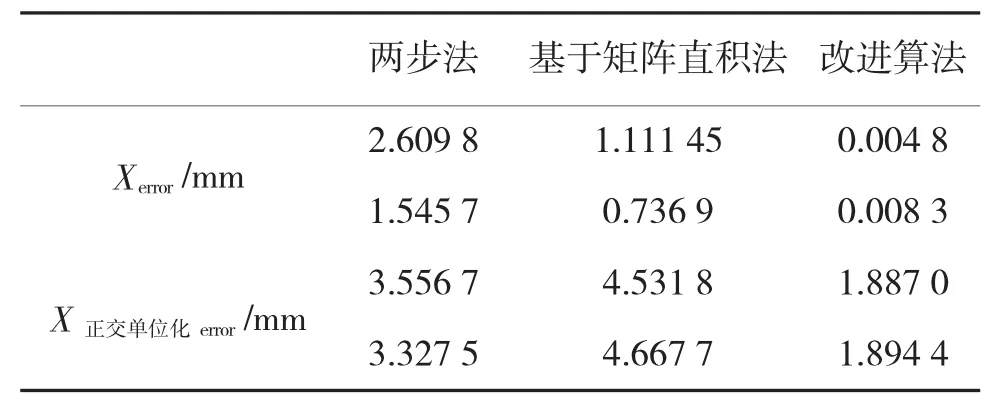
表3 平均误差分析
4 结论
通过多组实验数据验证了基于矩阵直积改进算法的鲁棒性很高。从两步法和数学法这个角度分析,数学法在手眼标定方面精度要高于传统的两步法。其次,改进算法采用的线性化处理的计算精度要高于非线性的算法。非线性化的两步法误差较大的原因很大方面来自于旋转矩阵的误差传递。一般性的基于矩阵直积算法并未实现真正的一步法,通过本文介绍的一般性矩阵直积算法可知,求解比例因子以及特征向量都会产生误差传递。实验证明:本文提出的一步化求解的改进算法在标定过程中具有误差幅度小,鲁棒性强等特点。

