飞行器用液氢贮箱低温推进剂晃动热力学响应分析

李 文,陈叔平,赵高逸,谢高峰

(1.兰州理工大学石油化工学院,兰州 730050; 2.北京航天发射技术研究所,北京 100076)

1 引言

随着航空、航天技术的快速发展,飞行器的探测范围和续航时间明显增加,飞行器所携带液体推进剂的比重不断增大,飞行器在姿态调整过程中贮箱内推进剂发生剧烈晃动,即充液容器在外部激励作用下自由界面波动或容器强制运动所引起的流体整体运动现象[1-2]。而低温推进剂密度大、粘度小,外部微小振动或晃动激励即可引起罐内流体大幅非线性晃动,严重威胁飞行器系统稳定性和结构安全性,且该现象自20 世纪五六十年代就已引起国内外研究人员的广泛关注[3-5]。

在一定漏热环境下,外界扰动所产生的低温推进剂晃动不仅会对贮箱产生附加力矩,还将引发贮箱内气液相间热力学不平衡等现象。刘展等[6-7]针对非等温贮箱晃动动态响应进行了分析。Isaacson 等[8]针对圆柱形贮箱作简谐运动和不规则运动时的液体晃动特性,定性分析了外部激励与自由液面波形的关系。Ludwig 等[9]在圆柱形贮箱中用液氮进行了实验,根据不同的晃动试验,建立了Nusselt 数和Reynolds 数,以反映箱体压降与晃动特性之间的关系。Das 等[10]采用FC-72 与HFE7000 为工质,实验研究了在稳定区以及非稳定区,轴向激励对箱体热力特性的影响,研究指出,箱体压力变化与外部激励大小有直接关系。Kassemi 等[11]采用数值模拟分析横向加速度引起的晃动对贮箱传热和压降的影响。Montsarrat[12]以储罐压降为重点,预测了液氢贮箱中的晃动热力学性能。李培昌等[13]研究发现贮箱内气液界面在晃动激励作用下被扰动,导致气相冷凝增加,贮箱内压力迅速降低等现象。Berglund 等[14]对液氢贮箱的相关预测表明,液氢可能被注入排气口和泄放系统,导致推力不平衡和控制失效。2020年12月9日,Space X 对星舰运载器一枚原型试验箭进行了首次高空飞行测试。但在着陆过程中,由于头部燃料贮箱压力过低,导致着陆速度过快,飞船发生爆炸[15]。因此,为保证低温贮箱的安全运行,有必要对飞行器用贮箱内液氢晃动热力学响应进行深入研究。

本文针对飞行器用160 L 高真空多层绝热液氢贮箱,数值模拟研究不同的晃动激励、初始液体温度和初始充满率下的晃动热力学特性,旨在为飞行器用低温液氢贮箱防晃设计及优化提供技术参考。

2 计算模型

2.1 VOF 模型

液体晃动过程中,液氢的流动是一个自由界面运动的问题,且液氢贮箱内始终存在气液界面,本文采用流体体积方法(Volume of Fluid,VOF)模型捕捉对相界面进行追踪。VOF 方法是一种在固定的欧拉网格下的表面追踪方法,其根据相份额φq的值来确定自由界面,如式(1)所示:

界面质量、动量以及能量平衡通过加载到离散项中的源项实现,用于求解该过程的控制方程。连续性方程如式(2)所示:

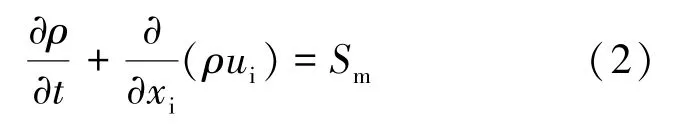
式中:ρ为密度,ui为平均速度矢量,Sm为源项。

动量方程如式(3)所示:

式中,ρ为密度;P为静压;τij为应力张量;gi和Fi分别为i 方向上的重力体积力和外部体积力,Fi包含其他模型相关源项。应力张量由式(4)给出:

式中,τij为应力张量;μ为动力粘度;ui、uj分别为i、j 方向上的平均速度矢量。

能量方程如式(5)所示:

式中,ρ为密度;u为流体速度;T为温度;cp为比热容;k为流体换热系数;gradT为温度梯度,用来表示温度的变化率;Sh为流体的内热源及由于粘性作用流体机械能转换为热能的部分,简称粘性耗散项。

在外部漏热作用下,气液界面会发生传热传质过程。相变模型采用Lee 模型,该模型假设界面相变发生在恒压和准热平衡状态下,如式(6)所示:

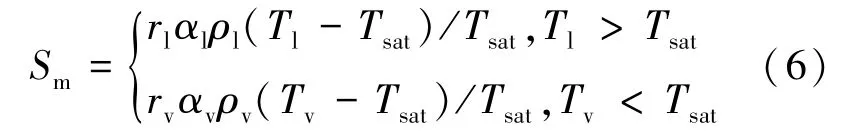
式中:Sm为质量能量源项;rl、rv分别为液相、气相的气化潜热;αl、αv为液相、气相所占相份额;Tl、Tv为液相、气相温度;Tsat为饱和温度。

2.2 数值模型

研究所用液氢贮箱为球形贮箱,主要由内容器和外壳组成。因内容器中液体晃动是本文重点研究内容,为简化问题,仅针对内容器建模。图1 展示了本文所研究液氢贮箱,其内容器直径为700 mm,壁厚为2 mm,罐壁材料为5083 铝合金。贮箱外部环境温度为293 K,与低温流体间存在较大温差,部分环境漏热q将渗入低温贮箱。为研究贮箱内流体晃动问题,对贮箱施加水平晃动激励,并在箱体内部气相区设有压力监测点以研究贮箱内流体动力特性,具体如图1 所示。为节省计算资源,采用二维模型计算求解。

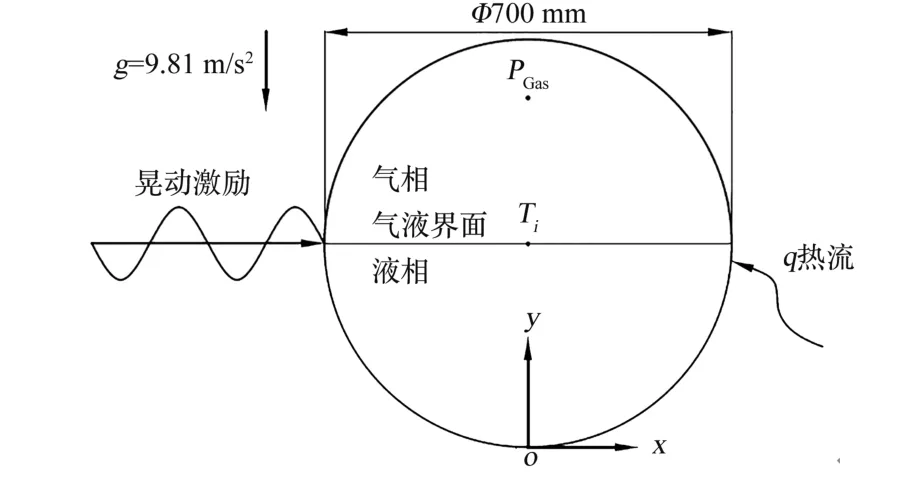
图1 低温液氢贮箱内罐示意图Fig.1 Schematic diagram of the inner tank of a cryogenic liquid hydrogen tank

2.3 网格划分

采用ANSYS 自带前处理软件Meshing 对液氢贮箱进行网格划分。计算采用结构化网格,近壁处进行加密处理,网格模型及网格无关性验证如图2 所示。飞行器机动过程中晃动激励为0.11 m/s 时,选择了3 种不同数量(70 967、115 489 与173 892)的计算网格进行网格无关性验证。对比不同计算网格下的晃动力变化可知,3种计算网格下箱体所受晃动力几乎完全重合,晃动力波动趋势存在微小差异,表明网格数量对箱体所受晃动力的影响较小。因此,为减少计算资源并提高计算精度,选择数目为115 489 的网格进行后续数值模拟研究[16]。

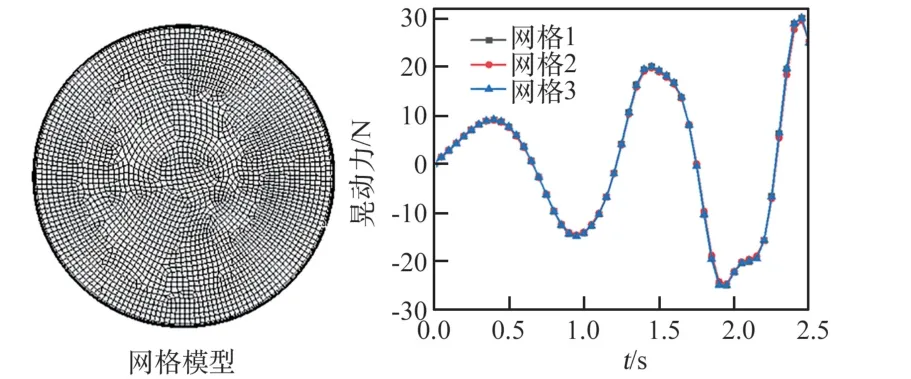
图2 网格模型及无关性验证Fig.2 Grid model and grid independence verification

2.4 初始条件

Agui 和Arndt 等[17-18]针对低温杜瓦内所做实验和数值结果表明,贮箱内的实际温度分布呈热分层状态,即气液相间无温度阶跃。为保证贮箱发射前气液相间温度良好的过渡,液相初始温度为20.0 K,在同一初始充满率不同晃动激励、不同初始液体温度及不同初始充满率下的气枕区域从界面处(20.0～21.5 K)到贮箱顶部(25 K)采用线性温度分布如图3 所示。罐内初始充满率50%,即液位高度 350 mm,初始气枕压力0.15 MPa。

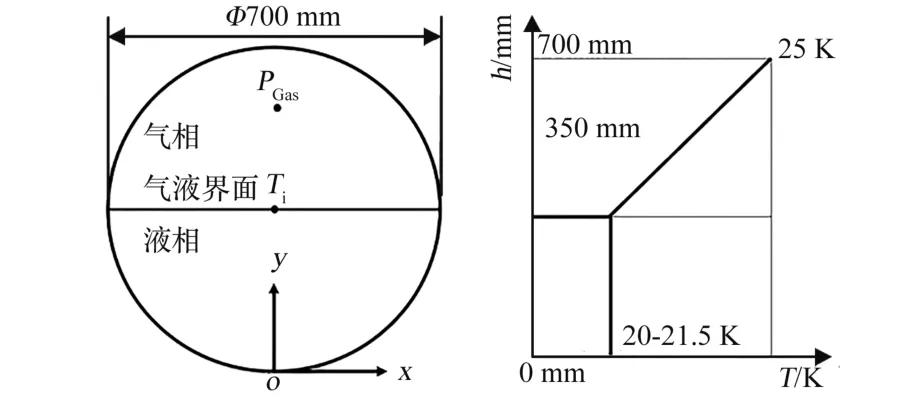
图3 液氢贮箱内初始温度分布Fig.3 Initial temperature distribution in the liquid hydrogen tank

2.5 边界条件

2.5.1 晃动激励

为模拟飞行器用液氢贮箱晃动,选择不同频率不同振幅的简谐激励作为动量源项添加到计算模型中。相应的简谐波动方程如式(7)所示:

式中,A为横向激励振幅,本文所取振幅分别为0.018 m、0.036 m、0.071 m;激励频率f=1.0 Hz;t为时间,计算步长为0.001 s。

贮箱与飞行器具有相同的飞行速度,可对贮箱壁面施加飞行器运行的速度边界条件(后文简称晃动激励),以模拟贮箱内部的液氢晃动,模拟设置中,在x轴方向(如图1 所示)对贮箱罐壁施加如下速度晃动激励,作用时间为2.5 s。

相应的速度晃动激励如式(8)所示:

式中,v为速度激励,通过位移激励x求导得到,表示为x＇。

为实现液氢贮箱所受到的简谐激励,本文通过编写用户自定义函数(User Defined Function,UDF)并结合动网格技术对气液界面波动过程进行有效预测。

2.5.2 漏热热流密度

外界热流量进入贮箱的途径,主要包括通过绝热层、管路及玻璃钢支撑结构的漏热量。

通过绝热层的漏热量如式(9)所示:

式中,λMLI取0.000 22 W(m·K)为高真空多层绝热表观导热系数,MLI 表示多层绝热,A为绝热层表面积,Ta取293 K,Td取20 K 分别为环境温度及介质温度,通过绝热层漏热量为3.66 W。

通过气相管的漏热量如式(10)所示:

式中,λ为5083 铝无缝管热导率,单位W/(m·K);Fe为气相管的换热面积,单位m2;Le为气相管的管长,单位m;Ta、Td分别为环境温度和介质温度,单位K。

通过液相管的漏热量如式(11)所示:

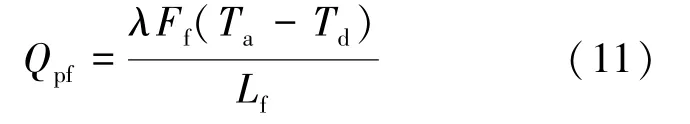
通过管路的综合漏热量为2.30 W,如式(12)所示:

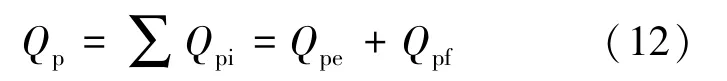
通过玻璃钢支撑结构的综合漏热量如式(13)所示:

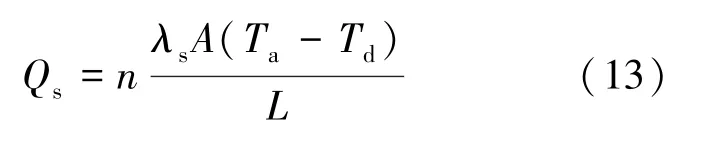
式中,n为支撑结构数量;λs为玻璃钢热导率,单位W(m·K);A为玻璃钢横截面积,单位m2;L为玻璃钢长度,单位m;Ta、Td分别为环境温度和介质温度,单位K。通过玻璃钢支撑的综合漏热量为2.25 W。

通过绝热层、管路和玻璃钢支撑结构进入液氢贮箱的总漏热量如式(14)所示:

式中,Q为液氢贮箱总漏热量,8.21 W。通过内容器壁面的漏热热流密度:

式中,为内容器外表面的面积,1.56 m2。

数值模拟中,对漏热热流做时均化处理,均视为第二类边界条件,其值为5.26 W/m2。

2.6 求解设置

采用Fluent 双精度求解器对液氢储罐内液氢晃动的热力耦合特性进行瞬态数值模拟。贮箱内气枕空间增压气体为氢气,计算工质为液氢。氢气采用理想气体模型,液氢密度采用Boussinesq假设,运动粘度等参数均参考物性软件NIST。参量的离散格式设置如表1 所示。

表1 离散格式Table 1 Discretization scheme

2.7 数值模型验证

由于液氮在物理性质上与液氢最为接近,而流体的晃动与运动粘度直接相关,液氮与液氢的运动粘度较为接近,标况下二者比值如式(16)所示:

式中,υLN2为液氮运动黏度,υLH2为液氢运动黏度。

采用软件ANSYS Fluent 19.0 模拟Lacapere[19]和Agui 等[17]针对立式低温恒温器所进行的液氮晃动实验,以验证本文所构建数值模型的有效性和准确性。模拟过程中的初始条件和边界条件与实验保持一致,计算处理与设置与本文所构建模型相一致。获得了低温恒温器内气枕压力值。因液氮晃动实验过程重点关注低温恒温器内部压力变化,此处选取实验值与模拟结果进行对比,两者之间的相对误差如图4 所示。

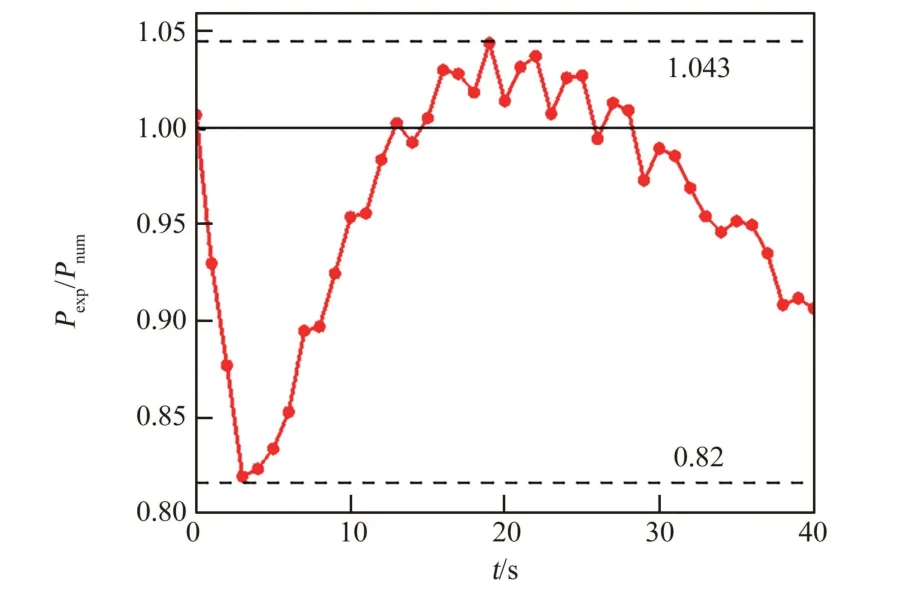
图4 实验值与模拟值间的相对误差Fig.4 Relative error between the experimental value and the simulated value

由图4 可知,气枕压力降幅高于实验,原因在于数值模拟未考虑气液界面附近的液相热分层。在40 s 的数值计算过程中,除前9 s 和后3 s 的模拟值与实验值存在较大偏差(最大为18%)外,其余时间两者误差均小于5%。结果表明,本文所构建的数值模型可用于运载飞行器用液氢贮箱内液氢晃动热力学响应的研究。

3 结果与讨论

3.1 不同晃动激励下晃动热力性能

为研究不同晃动激励对飞行器用液氢贮箱内热力学性能的影响,比较了晃动激励为0.00 m/s,0.11 m/s,0.22 m/s,0.44 m/s 时液氢贮箱内气枕压力的变化情况,气枕压力变化曲线及贮箱温度场分布分别如图5 和图6 所示。

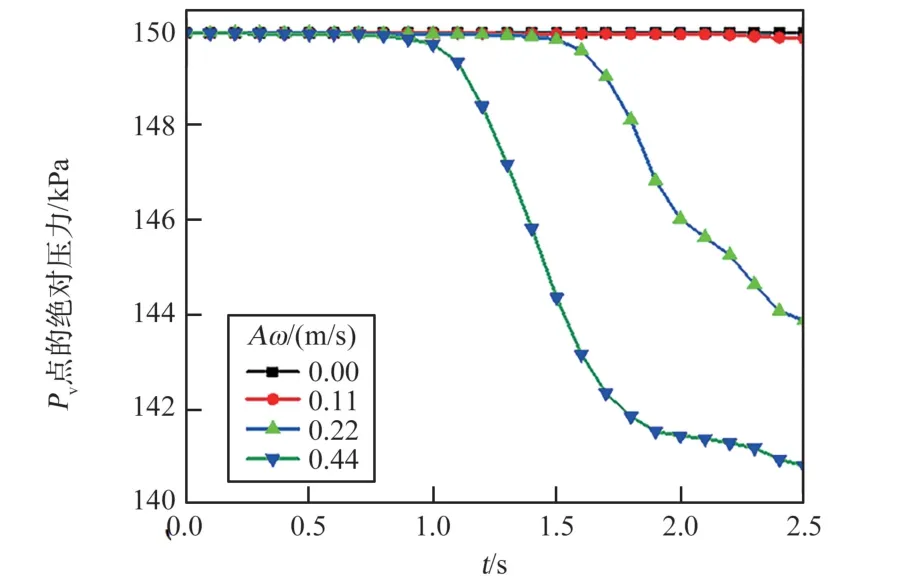
图5 气相测点Pv 处压力变化曲线Fig.5 Pressure change curve at the gas phase measurement point Pv

由图5 可知,当施加不同晃动激励时,贮箱气枕压力并未立即迅速降低,随晃动激励的扰动,破坏了贮箱内热力学平衡。①当晃动激励为0 m/s时,因环境热量漏入罐中,气枕压力出现先降后升的趋势,最大压降2 Pa,最大压升15.4 Pa。②当晃动激励为0.11 m/s 时,在2.5 s 的数值模拟过程中,气液界面附近的两相流只出现了小幅晃动,压力曲线呈现出小振幅的线性响应,最大压降120.3 Pa。③当晃动激励为0.22 m/s 时,贮箱内液体表现出较强的非线性响应。结合温度云图6(c)可知,1.6 s 时液体以剪切流的形式到达气枕空间,同时由于外界晃动激励的作用,贮箱内流体往复运动,致使剪切流发生波浪破碎,产生大量飞溅液滴,气枕压力出现大幅下降的拐点,直至压降速率达到最大后,贮箱内被扰动的热力学状态重新达到平衡,最大压降为6084.5 Pa。④当晃动激励为0.44 m/s 时,压力曲线表现出高振幅的非线性响应。前1.1 s 气枕压力线性降低,1.3 s 后,液体波浪到达气枕空间,并夹带大量过热气体。相比0.22 m/s 而言,液体到达气枕空间后产生更多量的飞溅液滴,导致气、液相间接触面积急剧增大,在增强气、液两相间换热的同时伴随着相变传质,导致气枕压力大幅降低,气枕空间最大压降9158.3 Pa。

图6 不同晃动激励下温度场分布云图Fig.6 Temperature contour under different sloshing excitations

总之,气枕压力随晃动的进行持续降低,且晃动激励越大气枕压力降幅越大,晃动激励为0.11、0.22、0.44 m/s 时的气枕压降分别为120.3、6084.5、9158.3 Pa。

由图7 可知不同晃动激励下气液界面处测点Ti处温度随时间的变化规律。在未施加晃动激励时,测点温度微幅波动升高,最大增幅为0.05 K;晃动激励为0.11 m/s 时,测点温度小幅波动升高,最大增幅为0.315 K;晃动激励为0.22 m/s 时,在2.08 s 之前,测点温度波动升高,最大增幅为1.809 K,在2.08 s 后,受流动粘性及阻尼运动的影响,测点温度随时间波动降低。晃动激励为0.44 m/s 时,与晃动激励为0.22 m/s时测点温度的波动变化趋势相似,在1.91 s 之前,测点温度波动升高,最大增幅为1.392 K;随后受流体粘性及阻尼运动的影响,测点处温度波幅逐渐减小。

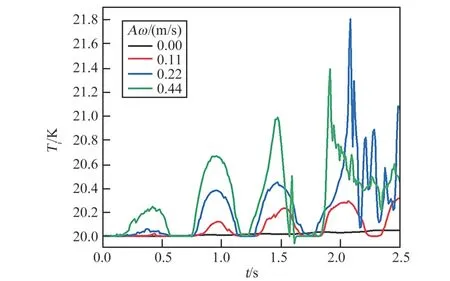
图7 不同晃动激励下气液界面测点Ti 温度变化Fig.7 Temperature change at point Ti of gas-liquid interface under different sloshing excitations

由以上分析可知,在2.5 s 的数值计算时间内,不同晃动激励下气液界面处测点Ti处的温度随时间波动增大,且晃动激励越大,波动越剧烈。原因在于当施加不同晃动激励时,贮箱轴对称上的测点受气相传热及壁面自然对流作用,被加热液体会向气液界面处流动积聚,因此,气液界面处测点温度随时间波动升高。

3.2 不同初始液体温度下气枕压力变化

当初始气枕压力为150 kPa 时,液氢的饱和温度为21.77 K,选择3 种初始液体温度分别为20.0、21.0、21.5 K,其值均小于液氢的饱和温度,即该温度下的液相皆处于过冷状态。

晃动激励为0.22 m/s、初始充满率为50%和初始液体温度分别为20.0、21.0、21.5 K 时气相测点Pv的气枕压力变化如图8 所示。

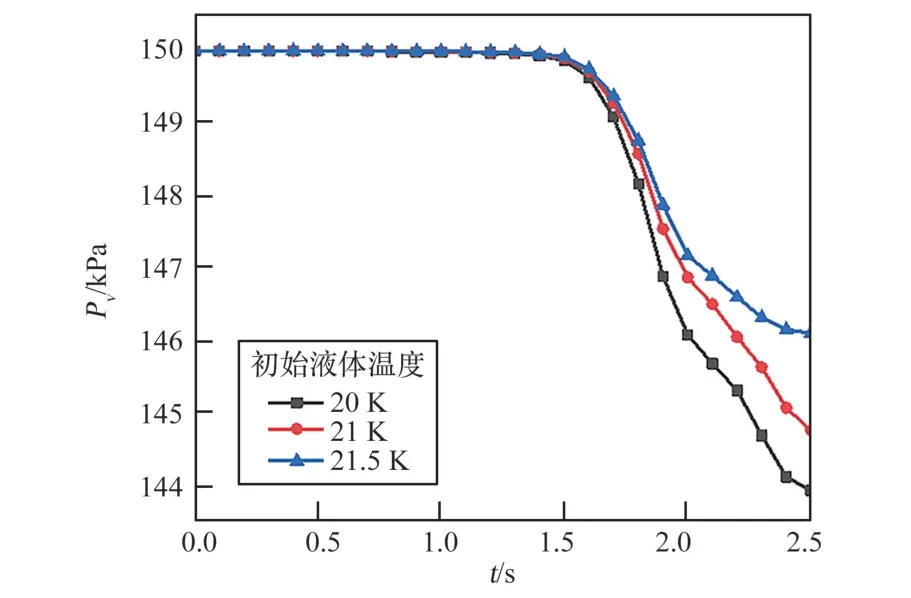
图8 不同初始液体温度下气相测点Pv 处压力变化Fig.8 Pressure changes at the gas phase measurement point Pv under different initial liquid temperatures

由图8 可知,在过冷液体冷凝下,前1.5 s 不同初始液体温度下的气枕压力随时间线性降低,1.5 s 后剪切流到达气枕空间,增大了气液相间接触面积。此外,对液氢而言,初始液体温度越低,过冷度越大,当晃动激励作用于罐壁,使得气液相间接触面积增大时,气枕空间过热气相被初始液体温度较低的液氢极大冷凝,致使气枕空间发生更大压降。因此,气枕压降随初始液体温度的降低而增大。当初始液体温度从20.0 K 升高到21.5 K 时,测点处的最终气枕压力值分别为143 921、144 752、146 098 kPa,相对应的压降分别为6079、5248 和3902 Pa。

3.3 不同初始充满率下气枕压力变化

为探究晃动激励为0.22 m/s、初始液体温度为20.0 K 和初始充满率分别为30%、40%、50%、60%、70%下的晃动热力性能,在罐体对称轴上设置了气相测点Pv(0,600)。该测点在不同初始充满率、同一晃动激励下的气枕压力变化曲线如图9 所示。

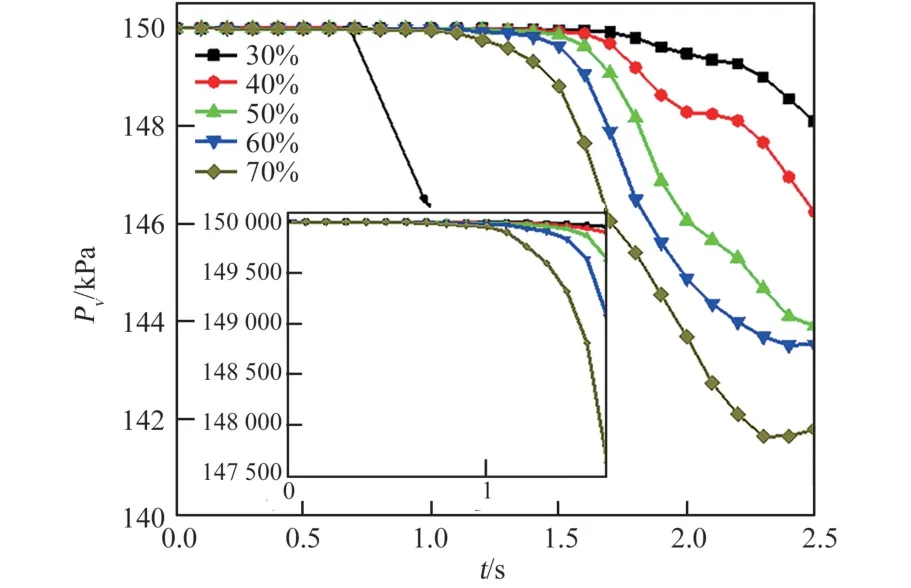
图9 不同初始充满率下气相测点Pv 处压力变化Fig.9 Pressure changes at the gas phase measurement point Pv under different initial full rates

由图9 可知,不同初始充满率下气枕压力不断降低,且初始充满率越高,过冷液体中贮存了更多的冷量,气枕压力降幅越大。随着初始充满率从30%增加到70%,气枕压力从150 kPa 下降到148 095、146 242、143 915、143 523.83 和141 661 kPa,相应的压降分别为1905、3758、6085、6476 和8339 kPa。

4 结论

采用CFD 技术数值模拟研究了外部晃动激励下飞行器用液氢贮箱内低温推进剂晃动热力学响应分析,结论如下:

1)晃动增强了过热氢气对过冷液体和罐壁的传热,晃动激励越大,气枕空间压降越大。

2)初始液氢温度对气枕压力有较大影响,气枕压降随初始液体温度的降低而增大。

3)初始充满率越高,过冷液体中贮存的冷量越大,气枕压力对界面的冷凝更敏感,气枕压降越大。

4)贮箱内压降受晃动激励、初始液氢温度及初始充满率的影响,其中外部晃动激励极大的扰动了液氢贮箱内气液界面处的热力学平衡,导致贮箱气枕压力大幅降低,影响飞行器的稳定运行。因此,亟需采取合理的增压或防晃措施来维持贮箱压力的稳定性,为飞行器的安全运行提供保障。