齿轮齿条式惯质粘滞阻尼器的拉索减振机理研究

刘 菁，梁 栋,2，杨 柳，李英俊，熊章豪

(1. 河北工业大学土木与交通学院，天津 300401；2. 河北省土木工程技术研究中心，天津 300401)

斜拉桥更大的跨径及其舒适性与安全性是设计者与建造者共同追求的目标。但是，由不同致振机理导致的振动均会影响斜拉桥的使用，小幅度的振动会影响斜拉桥的舒适性，而剧烈的大幅振动会直接危及人民的生命与财产安全。特别是，拉索作为一种细长的构件，其横向刚度和自身阻尼很小。因此拉索在外荷载作用下，如：在车辆荷载、风荷载以及风雨作用下更易发生振动。拉索的大幅振动更是引起了国内外学者的广泛关注[1−11]。为抑制拉索振动，在实际工程中通常采取了多种多样的拉索减振措施，如：安装内置、外置、单端或双端粘滞阻尼器、增加辅助索或在拉索上缠绕螺旋线等。其中在拉索近锚固端安装被动式粘滞阻尼器是最为常用的方法。许多学者对粘滞阻尼器的性能和最优参数设计进行了广泛的研究[12−17]。随后，研究者们考虑了不同的非理想条件，包括阻尼器的非线性、内部刚度、支撑刚度、拉索的垂度以及索-梁之间耦合振动等不利因素的影响[17−18]，以优化阻尼器的阻尼系数并准确预测拉索的阻尼比。这些研究表明，粘滞阻尼器可以为指定的拉索振动模态提供最佳阻尼，但阻尼器安装位置到拉索锚固端的距离较通常较近[19−20]，这使传统粘滞阻尼器的减振效果很难得到进一步的提高。

在研究具有负刚度特性的阻尼器的过程中，研究者们发现负刚度元件可使阻尼器的两端产生更大的相对位移，从而消耗更多能量[21−26]。同时，具有较小物理质量的惯质元件可通过滚珠丝杠、齿轮齿条或杠杆摆等机构的作用，产生较大的惯性质量。因此，由惯质元件所产生的负刚度效应也逐渐用于结构振动控制。黄绪宏等[27]将惯质引入颗粒阻尼器，建立了考虑惯质的多颗粒阻尼器力学模型。张瑞甫等[28−30]分别针对安装混联I 型惯容减振系统(SPIS-I)与混联Ⅱ型惯容减振系统(SPIS-Ⅱ)的单自由度体系开展了随机地震响应的机理研究，并提出了振动控制的设计策略。LAZAR 等[31−33]使用惯质元件替换了调谐质量阻尼器中的质量元件，得到了调谐惯质阻尼器(TID)分析模型。针对拉索第一阶振动模态的减振分析表明，当阻尼器安装位置一定时，TID 比传统粘滞阻尼器具有更优的减振效果。CHEN 等[34−35]将被动负刚度装置应用于拉索-阻尼器减振系统，以克服由于阻尼器安装位置限制而引起的附加阻尼不足的问题，并讨论了由于负刚度引起的非线性阻尼力对拉索减振分析的影响。SHI 等[36−39]将弹簧和粘滞阻尼器并联形成负刚度阻尼器，通过数值分析和模型试验，验证了该阻尼器对拉索第一阶振型的减振性能远优于传统粘性阻尼器。NAKAMURA 等[40]、WANG 等[41]利用旋转式电磁阻尼器与滚珠丝杠式惯容器分别研发了电磁式惯性质量阻尼器(EIMD)，EIMD 通过滚珠丝杠的作用，使阻尼器能够以较小的物理质量与较低的阻尼系数，获得可观的惯性力与阻尼力。LI 等[42]提出了一种电磁并联阻尼器 (EMSD) 来模拟惯质阻尼器，开展了张紧拉索的室内振动控制试验。LI等[43]使用了一台电磁式惯性质量阻尼器 (EIMD)的新型阻尼器样机对135 m 长的张紧拉索进行减振试验和数值研究。

通过上述分析可知，目前将惯质类阻尼器应用于拉索减振的相关研究还很不充分，多偏向于理论研究，且阻尼器样机多以滚珠丝杠结合电磁元件实现。特别是在拉索-惯质粘滞阻尼器体系的振动控制方面还缺少详细深入的研究。为深入的分析惯质粘滞阻尼器对拉索的振动控制效果，本文设计并制作了包括齿轮齿条、惯质元件和阻尼元件在内的惯质粘滞阻尼器，开展了相应的理论分析、阻尼器耗能性能试验及拉索-阻尼器体系的减振试验。

1 新型齿轮齿条式惯质粘滞阻尼器

本文介绍的齿轮齿条式惯质粘滞阻尼器受力机理明确、齿轮齿条结构稳定可靠，能够承受较大荷载便于在实际工程中应用。拉索与齿条通过索夹片连接，拉索振动带动齿条进行上下往复运动，齿轮将齿条的直线往复运动转化为惯质圆盘和阻尼圆盘的转动；利用阻尼圆盘在阻尼液中的转动实现耗能[44−46]。

1.1 新型惯质粘滞阻尼器的组成及其力学参数

如图1 所示，惯质粘滞阻尼器由两部分组成：惯质元件和阻尼元件。其中，r1～r3分别为齿轮、转轴和阻尼圆盘的半径，惯质圆盘的半径为r5。拉索竖直方向的振动通过齿条和齿轮变为输入轴的转动，则转动部件的转角 θ和阻尼器产生的扭矩T可表示为[47]：

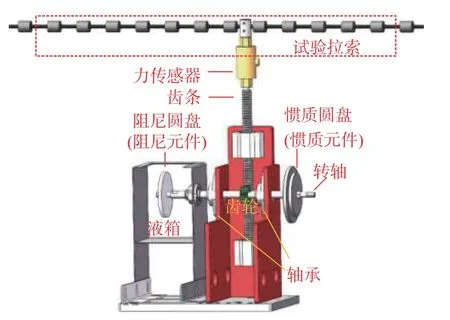
图1 惯质粘滞阻尼器的剖切图Fig. 1 Diagram of the viscous inertial damper

1.2 惯质装置的计算

新型惯质粘滞阻尼器中的转动、直线运动的部分，在运动过程中都会产生惯性扭矩和惯性力。式(2)中惯质元件所产生的扭矩Ti可表示为(下标i 为惯质首字母缩写)：

1.3 阻尼装置的计算

本文采用3 号锂基润滑脂和液压油按照1∶3 的体积比配合成粘滞阻尼液，阻尼扭矩Tc可表示为[48]：

1.4 阻尼力计算公式

2 阻尼器耗能试验结果及分析

目前，了解阻尼器力学性能的主要方法是性能试验。本文将阻尼器通过索夹将齿条与拉索连接，采取人工在拉索相应振型的反节点处采取相应的频率进行激振，当垂直振动幅度达到一定值时停止激励，让拉索做自由衰减振动。通过记录垂直振动的时程曲线，来研究不同工况(不同惯性质量与不同振动模态)下阻尼器的力学性能。振动数据通过MATLAB 中的带通滤波器以消除其他振动模态的影响[17]，阻尼器样机如图2 所示。

图2 阻尼器样机Fig. 2 Prototype of the damper

2.1 阻尼器性能评价所需参数的计算

将阻尼器的齿轮、转轴、阻尼圆盘、惯质圆盘的各项参数按照式(4)～式(6)计算并汇总于表1 和表2。

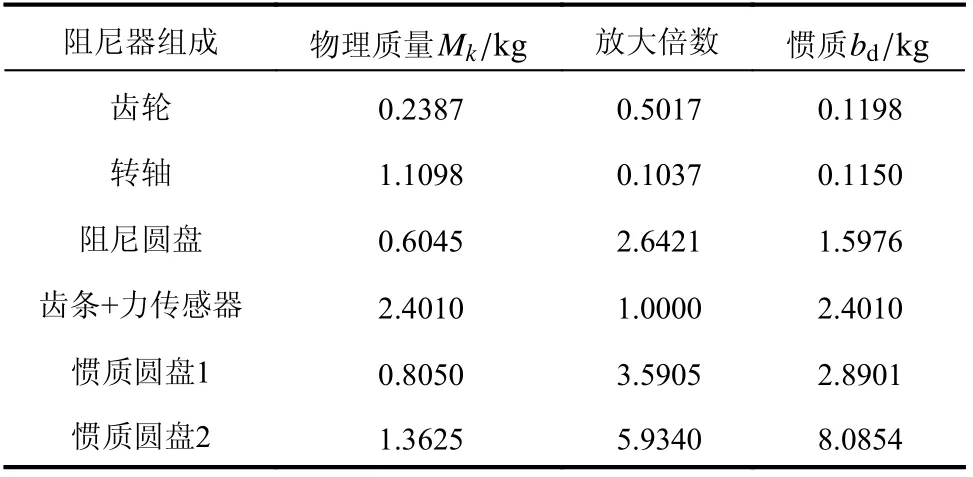
表1 阻尼器各组成部分Table 1 Damper’s parameters

表2 阻尼器的惯性参数Table 2 Damper’s inertial parameters

值得说明的是，该惯质粘滞阻尼器必须由齿轮、齿条、转轴和阻尼圆盘组成，因此该阻尼器样机惯性质量最小值为4.2334 kg。此外，根据不同减振目标模态的需求，选择了附加不同的惯质圆盘进行阻尼器耗能性能分析。

2.2 不同频率下的阻尼器耗能性能

在阻尼油箱中加入阻尼油并将阻尼圆盘安装于转轴上。阻尼圆盘在阻尼油中转动起到剪切阻尼油的作用，并且由于圆盘同时具有一定的惯质，也会同时起到提供负刚度的作用，如需增加惯质时，考虑在转轴另一端添加惯质圆盘。在惯质bd分别为4.2334 kg、10.0136 kg 和20.4042 kg，振动频率分别为1.92 Hz、1.77 Hz 和1.55 Hz 时(为阻尼器安装于拉索距锚固端2.3 m 时的一阶对称振动频率)，分别记为工况1、工况2 和工况3。惯质bd分别为4.2334 kg、10.0136 kg 和20.4042 kg，振动频率分别为3.17 Hz、2.77 Hz 和2.59 Hz(为阻尼器安装于拉索距锚固端2.3 m 时的一阶反对称振动频率)时，分别记为工况4、工况5 和工况6，工况汇总如表3。

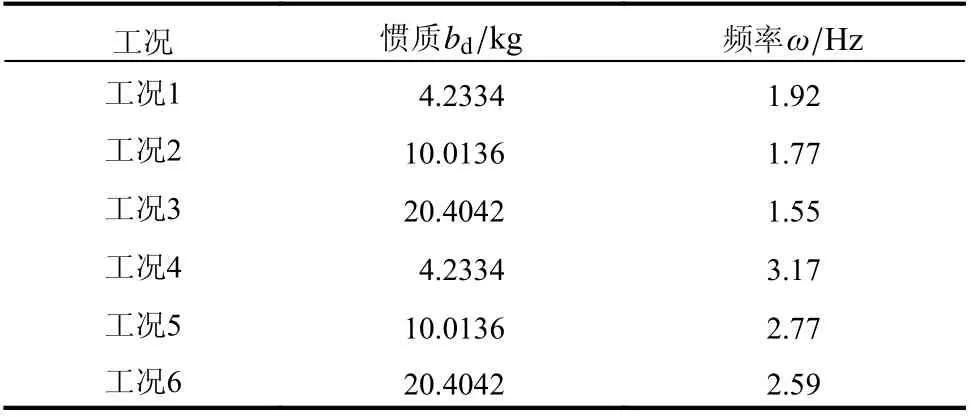
表3 各工况惯质、频率汇总Table 3 Summary of inertial and frequency of each case

根据工况1、工况2 和工况3 试验得到的滞回曲线采用最小二乘法拟合，根据式(9)可以确定惯质粘滞阻尼器的阻尼系数cd＝66.0079 N·s/m。工况1、工况2 和工况3 试验力-位移曲线与按式(10)计算的理论力-位移曲线分别如图3(a)～图3(c)所示，试验与理论所得的力-位移曲线包络面积与负斜率均近似相等。

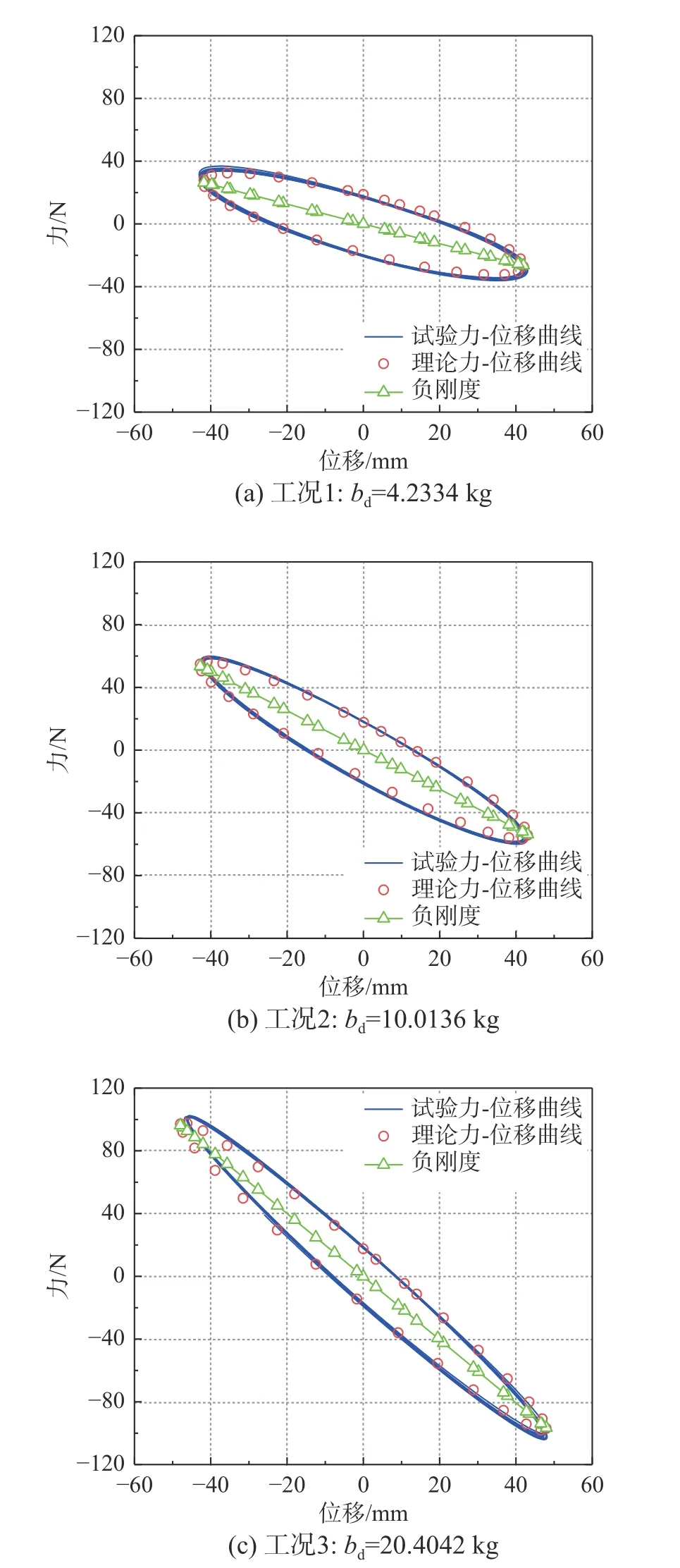
图3 滞回曲线Fig. 3 Hysteretic curve

根据工况4、工况5 和工况6 试验得到的滞回曲线采用最小二乘法拟合，根据式(9)可以确定惯质粘滞阻尼器的阻尼系数cd＝66.0079 N·s/m。工况4、工况5 和工况6 试验得到的力-位移曲线与按式(10)计算的理论力-位移曲线分别如图4(a)～图4(c)所示，试验与理论所得的滞回曲线包络面积与负斜率均相等。藉此，可以认为本文所述的阻尼液是较为稳定的。

图4 滞回曲线Fig. 4 Hysteretic curve

3 拉索－惯质粘滞阻尼器减振的归一化方程

为研究惯质粘滞阻尼器对拉索的减振作用，本文建立了如下理论分析模型，拉索平面静态构型如图5 所示。

图5 倾斜拉索的平面静态构型Fig. 5 In-plane static profile of inclined cable with sag

3.1 垂度拉索的平面内振动

考虑到有垂度拉索在阻尼器位置处的位移连续性条件，约去式(16)解中的时间项：

3.2 对称模态的波数方程

并将式(28)整理得到：

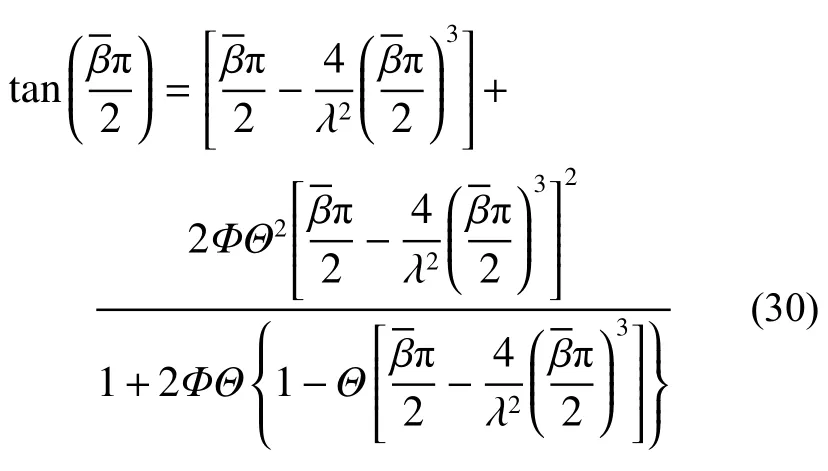
3.3 反对称模态的波数方程

3.4 张紧索的波数方程

根据式(21)，当λ2=0时，则式(21)左端第三项为零，可得张紧索的归一化波数方程为：

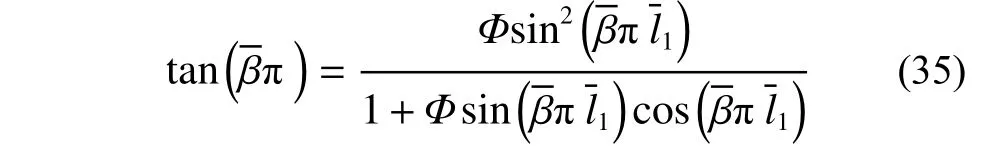
式(35)与文献[51−53]所述张紧拉索的波数方程相吻合。式(30)、式(33)和式(35)通过牛顿迭代法求解，可得到较为准确的计算结果。本文通过数值计算软件MATLAB，得到归一化的波数，而后通过式(36)计算模态阻尼比。

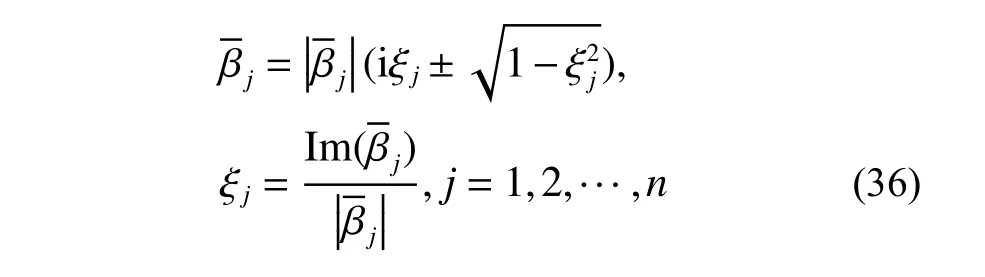
4 拉索-惯质粘滞阻尼器理论分析的试验验证

4.1 试验装置

考虑到试验条件和实验室具体情况，本文选用一根直径为9.3 mm 的钢丝绳作为拉索，水平锚固在反力架上。为降低拉索的自振频率，在钢丝绳上安装了小质量块。模型索-阻尼器试验系统如图6 所示，拉索各项参数详见表4。针对本次试验，用量程为50 kN 的压力传感器测量模型索索力；用量程为2.5 kN 的拉压力传感器测量阻尼力时程；用量程为±120 mm 的激光位移计测量模型索在距离拉索左端0.7 m、1.4 m、2.3 m、3.5 m 与对称位置处距离拉索右端1.4 m 和2.3 m 处的位移时程，①～⑥为激光位移计，⑦和⑧为力传感器，传感器布置如图7 所示。

图6 拉索振动控制试验Fig. 6 Test photo of cable vibration control

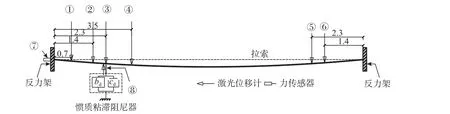
图7 试验模型传感器布置图 /m Fig. 7 Sensors’ location of the test model

表4 模型索的物理参数Table 4 Physical parameters of the model cable

4.2 拉索-惯质粘滞阻尼器系统减振效果分析

本文通过分析拉索自由振动的衰减速度，来考察阻尼器对拉索振动影响。采用的评价指标是模态阻尼比。在研究拉索的一阶对称振动时，激振位置为拉索跨中处；在研究拉索的一阶反对称振动时，激振位置为拉索远离阻尼器端的四分之一跨径处。待拉索按照相应的频率稳定振动后，立即停止激励的施加[17,43,54]。在本文试验中，忽略拉索内阻尼，通过快速傅里叶变换FFT，识别拉索各阶频率。无控拉索一阶对称振动频率为1.95 Hz，一阶反对称振动频率为3.63 Hz。拉索受控振动条件下，通过对拉索阻尼器安装位置处的时程曲线峰值进行拟合，可以求得拉索发生一阶对称振动、一阶反对称振动时的阻尼比。在拉索另一端，阻尼器安装位置的对称点处安装激光位移计，测量对称点处的时程曲线。通过比较阻尼器安装位置和拉索另一端对称点⑤的振幅，可以分析阻尼器对受控系统的位移放大效应。同时，按照式(24)将惯质粘滞阻尼器的参数进行归一化，将归一化参数代入式(30)与式(33)，并通过式(36)可得到模态阻尼比的理论计算值。各参数的归一化值详见表5。

表5 阻尼器各参数的归一化值Table 5 The normalized parameters of the damper

工况1、工况2 和工况3 的归一化惯质分别为0.13、0.3 和0.61，其一阶对称振动衰减曲线及其包络线分别如图8(a)～图8(c)所示；工况4、工况5 和工况6 的归一化惯质分别为0.13、0.3 和0.61，其一阶反对称振动衰减曲线及其包络线分别如图8(d)～图8(f)所示。

如图8 所示，通过比较阻尼器安装位置和拉索另一端对称点处的振幅，可以观察到惯质粘滞阻尼器在安装位置处对拉索的位移放大效应。本文给出了阻尼器安装位置处的实测阻尼比与理论计算阻尼比，验证了理论计算的准确性。同时，给出了实测频率，可以说明附加惯质粘滞阻尼器的拉索频率改变情况。分别将归一化惯质为0.13 时的工况1 和工况4 的试验结果与理论计算值汇总于表6，将归一化惯质为0.3 时的工况2 和工况5 的试验结果与理论计算结果汇总于表7；将归一化惯质为0.61 时的工况3 和工况6 的结果汇总于表8。

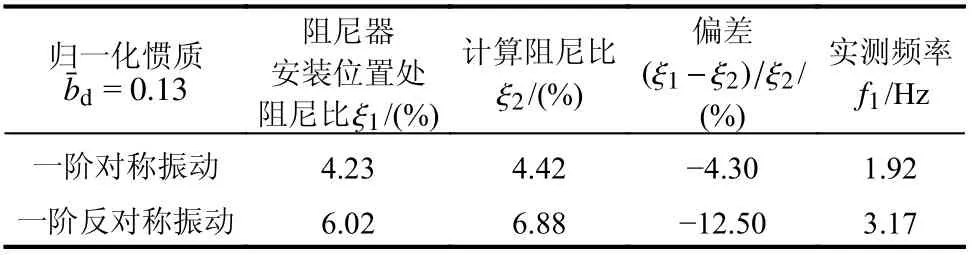
表6 阻尼比及频率结果汇总Table 6 Damping ratio and frequency summary and deviation

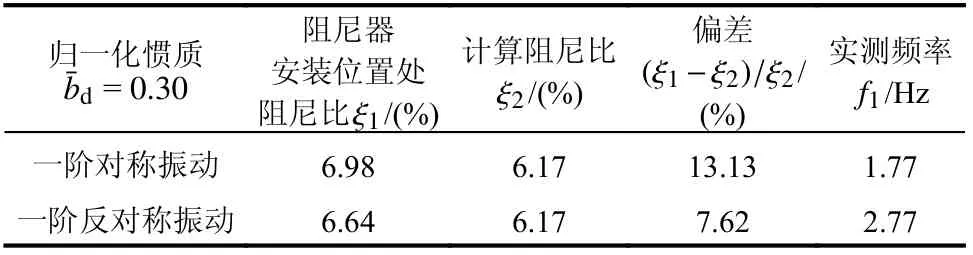
表7 阻尼比及频率结果汇总Table 7 Damping ratio and frequency summary and deviation

表8 阻尼比及频率结果汇总Table 8 Damping ratio and frequency summary and deviation

图9(a)～图9(c)分别给出了拉索一阶对称振动与一阶反对称振动的理论计算值与试验值的对比。将一阶对称振动的理论计算结果与图8(a)～图8(c)对比可知，归一化惯质越大，垂索在阻尼器安装位置处的位移放大效应越明显，能够使阻尼器消耗更多的能量，使一阶对称振动有较高的阻尼比。将一阶反对称振动的理论计算结果与图8(d)～图8(f)对比可知，在归一化惯质为0.13 与0.3 时，均产生了位移放大效应。此时，一阶反对称模态也获得了较高的阻尼比。而在归一化惯质为0.61 时，阻尼器处产生的位移小于拉索对称点上的位移，未产生位移放大效应，此时惯质对一阶反对称模态的阻尼比产生负面影响。

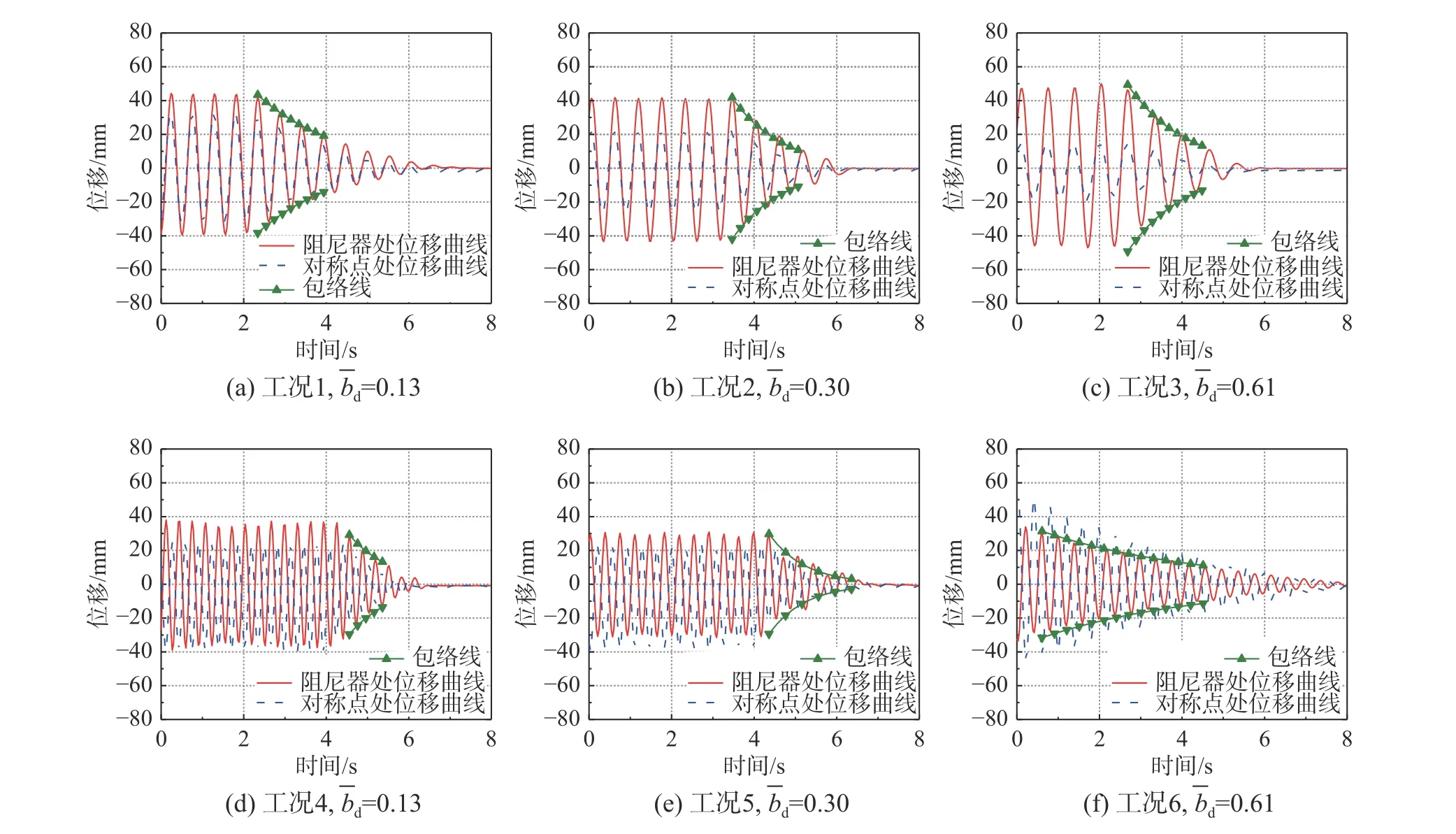
图8 振动衰减曲线Fig. 8 Vibration attenuation curve

5 减振机理探讨

5.1 惯质系数的影响

只考虑惯质bd时，式(30)、式(33)与式(35)的解为纯实数[37]。图10 表示了垂索一阶对称振动、垂索一阶反对称振动、张紧索一阶振动及张紧索二阶振动的归一化频率相对于归一化惯质系数变化的曲线。

由图10 可知，附加惯质会降低拉索的各阶模态频率，所有模态频率均随着归一化惯质系数的增加而降低。当=∞时，垂索一阶对称振动与张紧索一阶振动的归一化频率趋近于零；而垂索一阶反对称振动与张紧索二阶振动的归一化频率与长度为l2的无控拉索的相邻低阶频率接近(即总长为l2的未安装阻尼器拉索的频率，就像拉索一端被嵌固在阻尼器位置一样，即嵌固频率=1/l2)。同时，振型可看作是本阶振型按照附加惯质元件之后的修正值。本文针对垂度拉索的理论计算结果与文献[41]中的计算结果是一致的，垂索一阶反对称振动的归一化嵌固频率比张紧索二阶振动的归一化嵌固频率高是因为垂度项的存在，且垂索与张紧索的较高阶频率均比相应的低阶频率有更快的下降率。无论是张紧索或垂索，惯质粘滞阻尼器能够较为明显的改变拉索的各阶频率。

图10 归一化频率变化Fig. 10 The normalized frequency variation

5.2 阻尼系数的影响

当惯质bd分别为0.13、0.3 和0.61 的固定值时，改变归一化阻尼系数cd，求解式(30)和式(33)，可以分别得到垂索对称模态和反对称模态的归一化频率和归一化波数。求解式(35)可以得到张紧索的归一化频率和归一化波数。同时，因为有式(36)，求解得到的归一化频率与波数同时也可以说明图9 中模态阻尼比的变化规律。

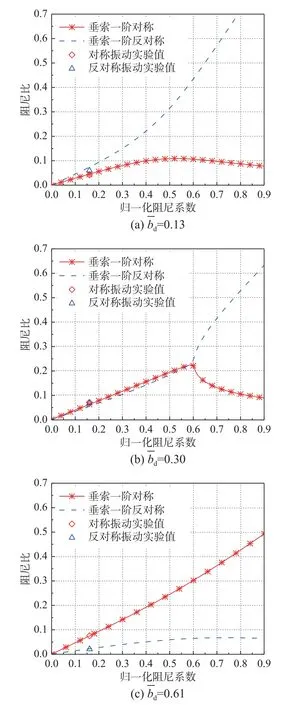
图9 试验与理论模态阻尼比的比较Fig. 9 Comparison between experimental and theoretical damping ratios

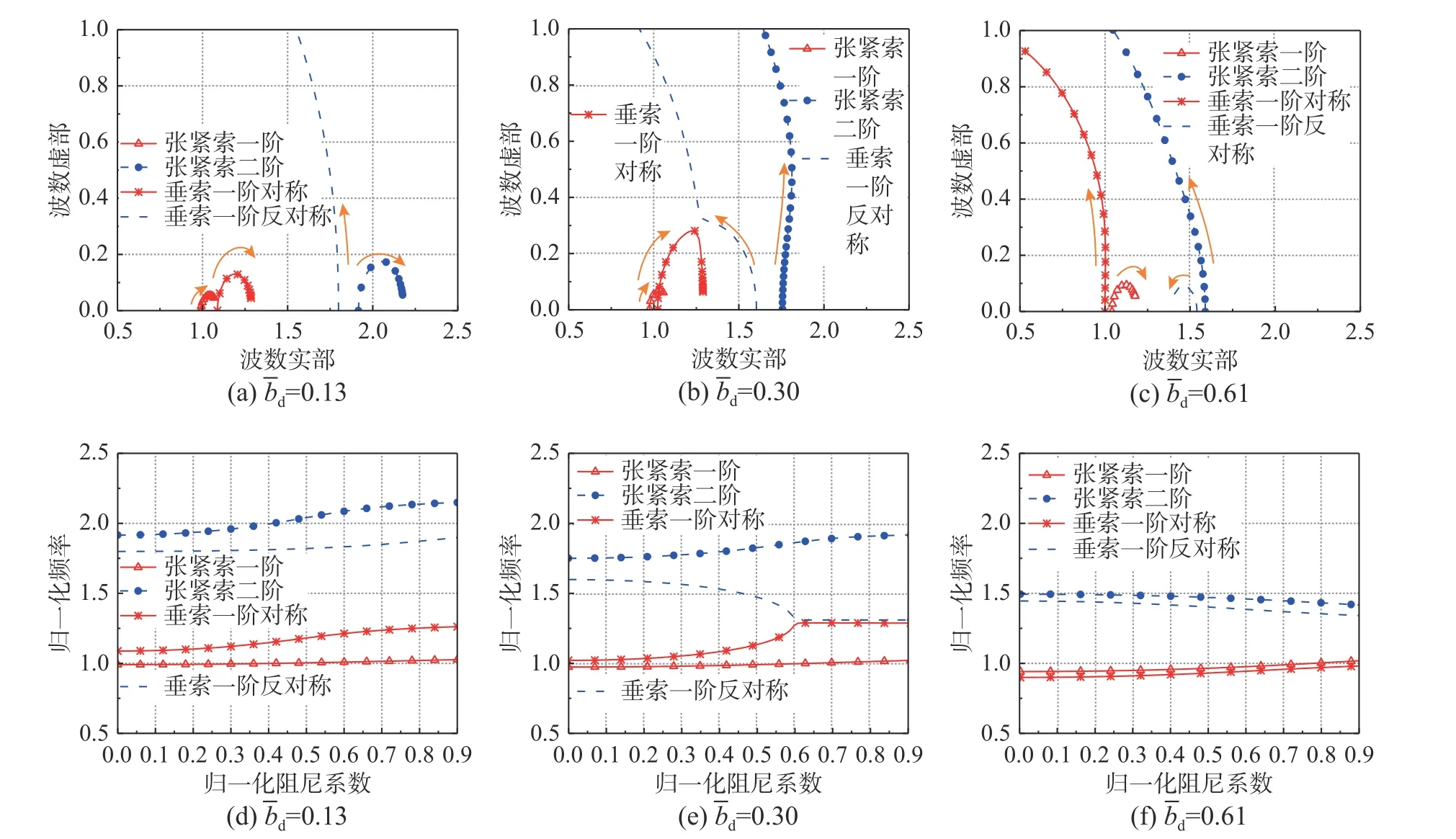
图11 波数与频率变化Fig. 11 Wave number and frequency variation

6 结论

本文对一种新型齿轮齿条式惯质粘滞阻尼器进行了归一化复模态分析和实验研究，详细分析了阻尼器的耗能性能及拉索-阻尼器体系的减振性能。本研究的主要结论总结如下：

(1) 通过试验，观察到了齿轮齿条式惯质粘滞阻尼器对垂度拉索的位移放大现象，这种位移放大现象能够使阻尼器耗散更多能量从而获得较高的模态阻尼比。

(2) 按照本文所述方法对各参数进行归一化后，当归一化惯质系数和归一化阻尼系数为优化值时，能够同时获得垂索的相邻两阶振动的最优阻尼比，且此时二者频率相同。

(3) 无论是张紧索或者垂索，惯质粘滞阻尼器能够较为明显的改变拉索的各阶频率，可以通过本文所述的方法对其进行分析。

(4) 对于安装齿轮齿条式惯质粘滞阻尼器的拉索，可以按照本文提出的方法，根据减振目标模态进行阻尼器参数设计。