螺旋筋约束增强钢-混凝土组合方柱偏压性能及承载力计算

周 济，陈宗平,2,3，周春恒，经承贵

(1. 广西大学土木建筑工程学院，广西，南宁 530004；2. 南宁学院土木与建筑工程学院，广西，南宁 530200；3. 广西大学工程防灾与结构安全教育部重点实验室，广西，南宁 530004；4. 宁波大学土木与环境工程学院，浙江，宁波 315211；5. 广西科技大学土木建筑工程学院，广西，柳州 545006)

空腹式角钢骨架型钢混凝土(SRC)柱和方钢管混凝土(CFST)柱是两类广泛应用于工业及民用建筑中的结构形式，其具备力学性能优良、节点构造简单以及施工进度快等优点[1−2]。但上述两类矩形截面约束混凝土柱均存在约束“拱效应”，即截面非均匀约束[3]，若不采取相应的措施改善其约束效力差的缺点，则很难满足现代高耸大跨建筑对结构高性能的要求。

针对如何改善角钢混凝土及方钢管混凝土柱约束性能差的问题，国内外学者展开了大量的试验研究，同时也得出了许多重要的结论，其中具有代表性的包括：采用内壁焊接加劲肋的方式虽不能够有效地提升方形CFST 柱的承载力，但可显著提升柱的延性[4]；布置对拉片或约束拉杆极大程度上消除了方形CFST 柱的约束“拱效应”，可以有效提升柱体的承载力和延性[5−6]；在方钢管内放置螺旋筋或内壁焊接圆形箍筋同样可有效提升柱体的承载力和延性[7−8]。对比上述研究中所采取的构造措施，可以发现内置螺旋筋可以免除焊接工序，施工高效的同时又可极大程度地改善方形CFST 柱的轴压性能。因此，将螺旋筋内置于角钢骨架或方钢管中后填充混凝土形成了螺旋筋约束增强钢混凝土组合方柱(以下简称“组合柱”)，具有良好的应用前景。为揭示钢-混凝土组合方柱内置螺旋筋的约束增强机理，明确螺旋筋设计参数对组合柱的约束增强效果的影响规律，国内学者陈宗平等[9−12]进行了系列试验研究，结果表明：螺旋筋有效改善了角钢骨架或方钢管对核心混凝土约束不均匀的特点，且随着螺旋筋间距的减小、螺旋筋直径和径宽比的增大，组合柱表现出更加优良的轴压性能，其原因是：当角钢骨架或方钢管内放置螺旋筋时，将对混凝土形成双重约束机制，螺旋筋可以弥补角部约束不足，起到改善矩形截面柱约束不均匀的作用。

此外，在核心混凝土内放置螺旋筋还可有效提升SRC 柱或CFST 柱的结构抗火性能，因此组合柱是一种综合性能较高的结构形式。然而，目前针对组合柱的研究主要集中于轴压性能方面，其偏压性能研究还少有涉及，尤其是偏压状态下螺旋筋约束增强效果及相关影响因素分析有待深入研究。基于此，本文设计了30 个组合柱(15 个角钢试件和15 个钢管试件)的偏压试验，观察了试件的破坏过程及模式，对比分析了各变化参数对试件偏压性能指标的影响，并讨论了复合约束下两类组合柱的刚度退化规律，最后根据压溃理论推导出螺旋筋约束增强钢混凝土组合方柱偏压承载力的计算公式。

1 试验概况

1.1 试件设计与制作

角钢混凝土方柱和钢管混凝土方柱同属于约束混凝土结构，从受力角度来看，二者均存在着核心混凝土的约束力较弱且分布不均匀问题。为研究内置螺旋筋对钢-混凝土组合方柱约束增强效果，根据《钢管混凝土结构技术规范》(GB 50936−2014)和《组合结构设计规范》(JGJ 138−2016)，设计并制作了30 个试件，其中包括15 个角钢试件(14 个螺旋筋-SRC 方柱、1 个SRC 方柱)和15 个钢管试件(14 个螺旋筋-CFST 方柱、1 个CFST 方柱)。试件的截面尺寸均为B×B=200 mm×200 mm，高度L=1600 mm。对于角钢试件，角钢的肢宽×厚度包括40 mm×4 mm 和50 mm×4 mm，扁钢缀条的宽度×厚度为40 mm×4 mm；对于钢管试件，钢管的壁厚包括3 mm 和4 mm；内配螺旋筋试件的纵筋分布包括4 10 和4 12；两类组合柱的截面及配钢形式如图1 所示。本试验的设计变化参数包括螺旋筋间距s、螺旋筋径宽比dc/B、纵向配钢率ρ 以及偏心率er，试件的详细设计参数见表1。试件制作时，将绑扎好的钢筋笼放入角钢骨架或钢管中，为确保二者的形心重合，采用在外部型材四边焊接连接筋的方式固定钢筋笼。

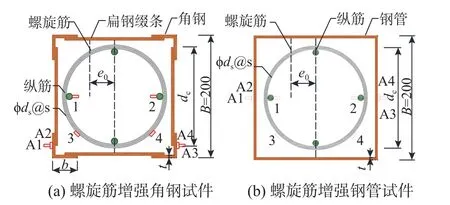
图1 配钢形式及应变片布置示意图 /mm Fig. 1 Layout of reinforcement and strain gauge

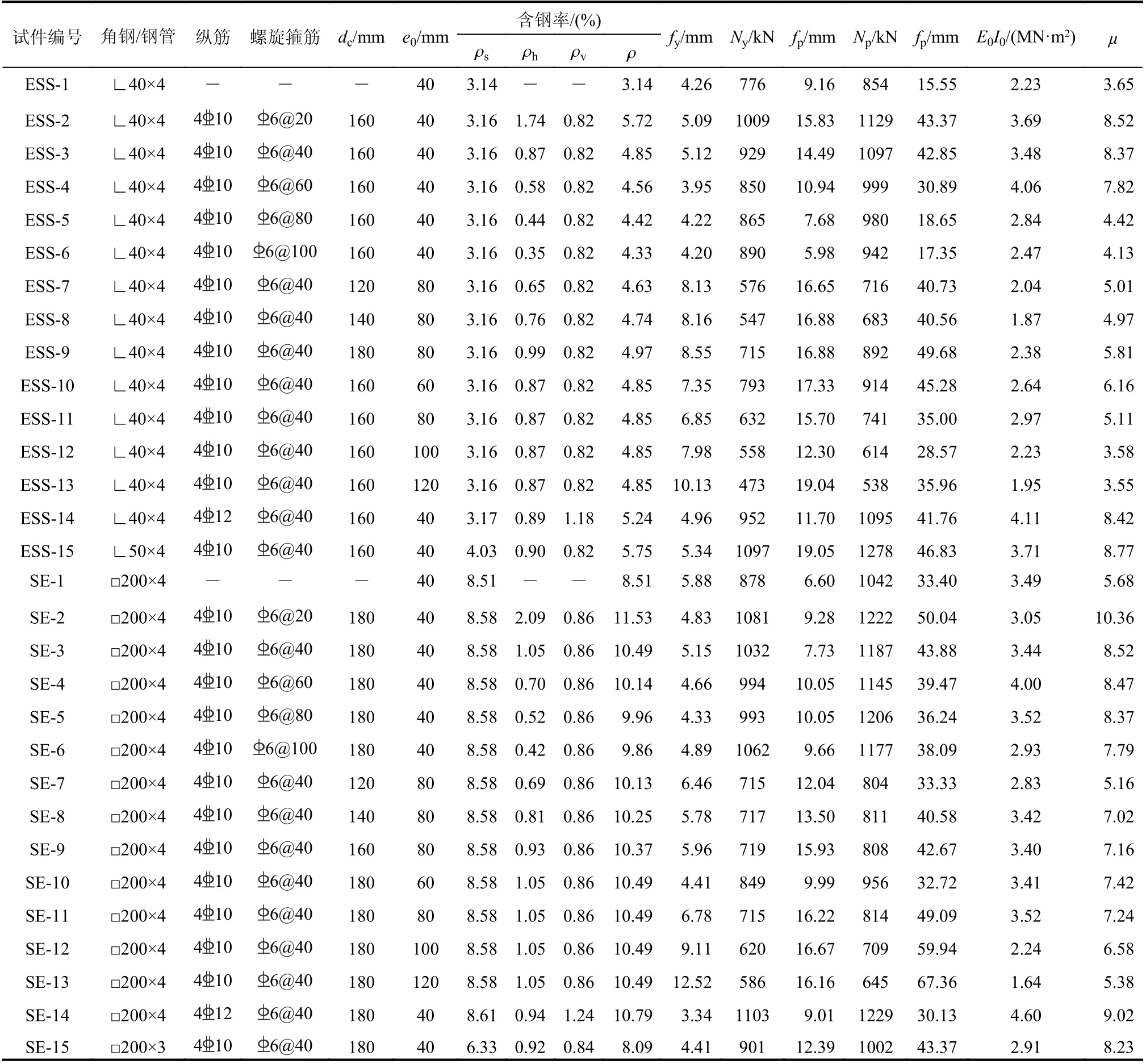
表1 试件参数及主要结果Table 1 Details of specimens and main results

1.2 材料力学性能

角钢骨架和方钢管均采用牌号为Q235 的碳素钢，其中方钢管为焊缝钢管，钢筋笼中的纵筋为HRB335 螺纹钢筋，螺旋筋为HPB300 光圆钢筋，钢材的实测力学性能指标见表2。所有试件采用同批次强度等级为C30 的商品混凝土进行浇筑，28 d实测混凝土立方体抗压强度为28.3MPa，弹性模量为27.5GPa，按照《混凝土结构设计规范》(GB 50010−2010)中计算公式算得混凝土轴心抗压强度为19.0MPa。

表2 钢材力学性能Table 2 Mix proportions of steel

1.3 加载装置及量测内容

偏压试验在YE-10000F 型电液伺服压剪试验机上进行，加载时在试件两端安装刚性夹头，以防止由于端部破坏而引起的试件过早失效；为达到试件偏心受力的目的，在试验机两端与试件之间设置滚轴支座，可通过改变滚轴位置控制偏心距大小；为获取试件的侧向挠度变形，在试件表面布置位移计量测，图2 为加载装置及测点布置图。试验采用位移控制的单调静力分级加载制度，速率为0.5 mm/min，每级位移增量1 mm，持荷3 min，当试件的荷载下降至峰值荷载的75%时加载试验终止。角钢、钢管、纵筋及螺旋筋应变，由按照图1 布置的应变片测得，应变数据采用DH3821Net 静态采集系统收集。

图2 加载装置及测点布置Fig. 2 Test setup and layout of measuring points

2 试验结果与分析

2.1 试件破坏模式

图3 为两类组合柱典型的偏压破坏形态。组合柱的偏压破坏过程及模式与对应的钢-混凝土柱相似。对于螺旋筋增强角钢试件，其破坏模式可分为大、小偏压破坏。根据试验破坏现象，发生大偏压破坏试件(e0>80 mm)的破坏过程表现为荷载约增至0.9Nu时受拉区角钢发生屈服，并伴随有斜裂缝或纵向裂缝出现在压区混凝土表面；接近峰值荷载时，受压区角钢也屈服，随着加载的进行受压区角钢逐渐向外屈曲，且受压区混凝土压碎剥落。发生小偏压破坏试件(e0≤80 mm)的破坏过程表现为，接近峰值荷载时受压区角钢发生屈服，并伴随有受压区混凝土压碎剥落；而峰值荷载时受拉区角钢及纵筋仍未屈服。内置螺旋筋后，受压区混凝土开裂破碎时间有所延缓，且最终的压溃程度也明显减小。对于螺旋筋增强钢管试件，其破坏模式也分为大、小偏压破坏。试验现象表明，发生大偏压破坏试件(e0>80 mm)的破坏过程表现为0.85Nu时受拉区钢管发生屈服，峰值荷载时受压区钢管与纵筋均屈服，且受压区钢管出现局部鼓曲。发生小偏压破坏试件(e0≤80 mm)的破坏过程表现为，峰值荷载时受压区钢管发生屈服，随即出现局部鼓曲，而此时受拉区钢管及纵筋并未屈服。

图3 试件破坏模式Fig. 3 Failure pattern of specimens

通过分析钢管试件的鼓曲过程发现，受压侧钢管距上、下端板1/4 试件高度范围内首先出现局部鼓曲，鼓曲沿试件跨中基本对称分布，尤其是钢管壁较薄的试件SE15 出现的鼓曲数量较多，但与普通钢管混凝土试件相比，鼓曲发展比较缓慢；峰值荷载时，试件中部±150 mm 范围内出现多处鼓曲，且鼓曲不断向四周扩大，但仅试件腰部附近有1～2 处鼓曲发展为控制性鼓曲波带，鼓曲宽度约为截面宽度，此时试件的挠曲变形明显；当控制性鼓曲带与其相邻两侧面鼓曲连通时，试件的荷载逐渐下降，最大鼓曲程度可达25 mm～30 mm。由此可见，内置螺旋筋后，受压区钢管鼓曲有所延缓，且局部鼓曲部位明显增多，从而避免了偏压作用下钢管混凝土柱局部变形过大引起的承载力丧失较快。两类组合柱的偏压破坏过程表明，内置螺旋筋提供的约束作用，既能减缓内部混凝土的压碎流动，又可降低受压区混凝土的破碎程度，进而降低了试件的局部破坏程度。

2.2 荷载-跨中挠度曲线

图4 为所有试件的实测荷载-跨中挠度曲线。由图4(a)可见，与无螺旋筋增强试件对比，两类组合柱的荷载-跨中挠度曲线峰值荷载及峰值位移更大，下降段更加平缓，且随着螺旋筋间距的减小，上述规律更为显著。由图4(b)可见，随着螺旋筋径宽比的增大，曲线的峰值荷载有所提升，但峰值位移及下降段趋势所受影响较小。由图4(c)可见，纵向配钢率的增大对试件的峰值荷载提升显著，对试件的峰值位移和下降段趋势影响较小，且外部角钢/钢管纵向配钢率相较于内部纵筋的影响更为显著。由图4(d)可见，随着偏心率的增大，试件的初始刚度和峰值荷载显著减小，峰值位移逐渐增大，下降段逐渐减缓。根据荷载-跨中挠度曲线来看，螺旋筋参数对螺旋筋增强角钢试件曲线的形态的影响显著大于螺旋筋增强钢管试件，无论是曲线的峰值荷载、峰值位移，还是初始刚度、下降段，均变化更为显著。

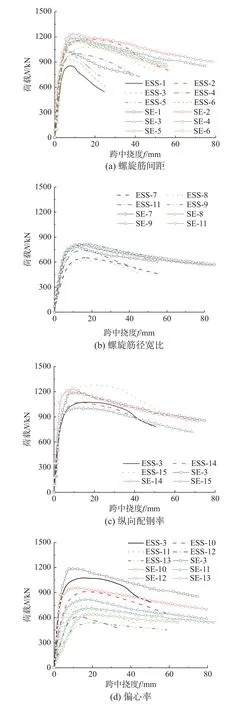
图4 荷载-跨中挠度曲线Fig. 4 Load-midspan deflection curves

2.3 荷载-应变规律

图5 为典型试件的偏压荷载-应变曲线，表3列出了特征点处典型试件各部分应变。结合图5和表3 来看，两类螺旋筋约束增强钢-混凝土组合方柱在偏压作用下的应变变化规律较为相似。当试件发生整体屈服时，角钢混凝土试件受压区混凝土应变大于2000 µε，内置螺旋筋后试件受压区混凝土应变减小了大约1/2，这也是试验中观察到的螺旋筋增强角钢试件受压区混凝土压溃程度明显减小的原因，受拉区混凝土应变始终保持在一个较低水平。而且，屈服荷载时大偏压试件受压、拉区纵筋与角钢/钢管的应变均接近屈服值，但小偏压试件只有受压区纵筋与角钢/钢管的应变均接近屈服值，受拉区的应变仍远小于屈服值。此外，无论在受压区还是受拉区，此时螺旋筋的应变值均很小，说明螺旋筋的约束作用尚未发挥。

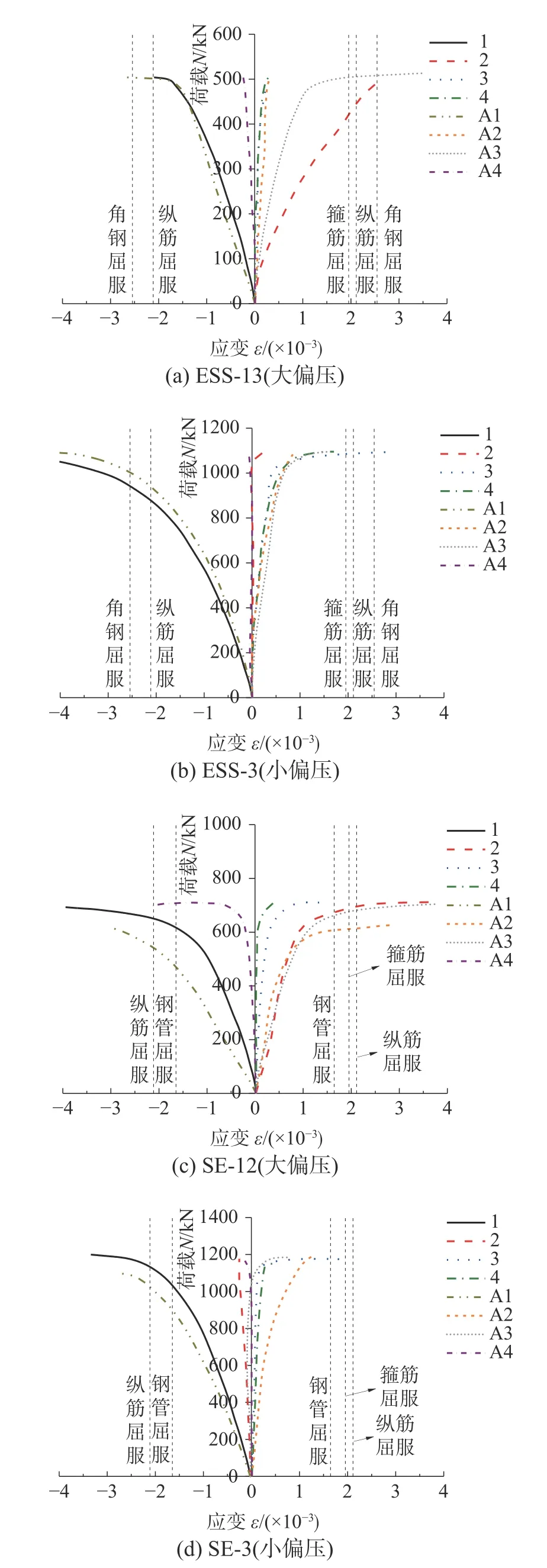
图5 典型偏压荷载-应变曲线Fig. 5 Typical eccentric load-strain curves

表3 典型试件特征点应变Table 3 Strain of typical specimen at characteristic point

在峰值荷载时，位于受压区的角钢/钢管以及钢筋的应变均达到屈服值；而位于受拉区的角钢/钢管以及钢筋，试件大偏压破坏时其已发生屈服，但小偏压破坏时其未能屈服。对于螺旋筋，其在峰值荷载处的应变值显著大于屈服荷载处，表明螺旋筋在试件到达峰值荷载时已产生了显著的约束作用。试件大偏压破坏时，无论是靠近加载点一侧，还是远离加载点一侧，其应变均未能在峰值荷载时达到屈服值；而在小偏压破坏时，靠近加载点一侧的螺旋筋在峰值荷载前发生屈服，远离加载点一侧则未发生屈服，出现这种现象的原因是：对于大偏压破坏试件，其受压区面积相对较小，混凝土挤压流动变形较小，螺旋筋被动提供的约束力尚未发挥。因此，组合柱在大偏压时不能充分发挥螺旋筋的作用。

3 两类组合柱性能对比

为对比两类组合柱偏压力学性能的差异，定量分析了螺旋筋间距、螺旋筋径宽比、纵向配钢率及偏心率对试件偏压力学性能指标(峰值荷载、抗弯刚度及延性系数)的影响规律，其中试件的抗弯刚度(E0I0)和延性系数(µ)利用实测的荷载-跨中挠度曲线依据文献[13]中的方法确定。

3.1 螺旋筋间距

图6 为螺旋筋间距对两类组合柱偏压力学性能指标的影响规律，其中∞代表试件未配置螺旋筋，即对照组试件。由图6(a)可知，对比未配置螺旋筋试件，两类组合柱的偏压承载力均有明显提升，其中螺旋筋增强角钢试件的最大提升幅度为32.2%，螺旋筋增强钢管试件的最大提升幅度为17.3%。此外，随着螺旋筋间距的增大，试件的承载力总体上呈逐渐降低的变化趋势，螺旋筋增强角钢试件和螺旋筋增强钢管试件承载力的最大降低幅度分别为16.6%和6.3%。一方面，说明内置螺旋筋产生的复合约束效应能有效提升角钢混凝土柱和钢管混凝土柱的偏压承载能力，且角钢混凝土柱获得的提升效果更为显著；另一方面，也说明当螺旋筋间距小于60 mm 时，减小间距并不能有效地提升组合柱的偏压承载力，且过密地布置螺旋筋往往因混凝土振捣不密实导致试件的承载力退化，这也是螺旋筋增强钢管试件在间距较小时承载力出现降低的原因。由图6(b)可知，合理的布置螺旋筋间距可显著提升试件的抗弯刚度，但螺旋筋过密时试件的抗弯刚度会被削弱，其原因是：布置螺旋筋后核心混凝土会在角钢约束或钢管约束的基础上形成双重复合约束，更有效地限制混凝土的变形流动，并提升混凝土的三轴抗压强度，从而实现试件抗弯刚度的提升；而核心混凝土的连续性也将对组合柱的抗弯刚度产生较大影响，若配置过密的螺旋筋会因混凝土振捣不密实而形成的非连续性导致试件的抗弯刚度降低。由图6(c)可知，对比未配置螺旋筋试件，两类组合柱的变形性能大幅提升，其中螺旋筋增强角钢试件和螺旋筋增强钢管试件的延性系数最大提升幅度分别为133%和82%，说明内置螺旋筋可显著改善角钢混凝土柱和钢管混凝土柱的偏压变形性能，且对角钢混凝土柱的改善更优。此外，随着螺旋筋间距的增大，试件的延性系数呈逐渐降低的变化趋势，螺旋筋增强角钢试件当间距达到80 mm 时下降显著，而螺旋筋增强钢管试件当间距达到40 mm 时下降显著，这是因为螺旋筋间距增大后约束效率降低使得混凝土的破坏提前，相较于间隔布置缀板的角钢骨架，钢管因其连续性对核心混凝土具备更好的侧向约束能力，在螺旋筋约束效率较高时才能凸显出对钢管混凝土变形性能的改善作用，而对角钢约束混凝土变形性能的改善作用则在较小的螺旋筋约束效率下就已凸显。综上所述，建议组合柱偏压受力时螺旋筋间距的取值范围为螺旋筋约束直径的2/9～4/9。由于此建议基于有限的缩尺模型试验，因此其施工可行性有待足尺试验进一步验证。

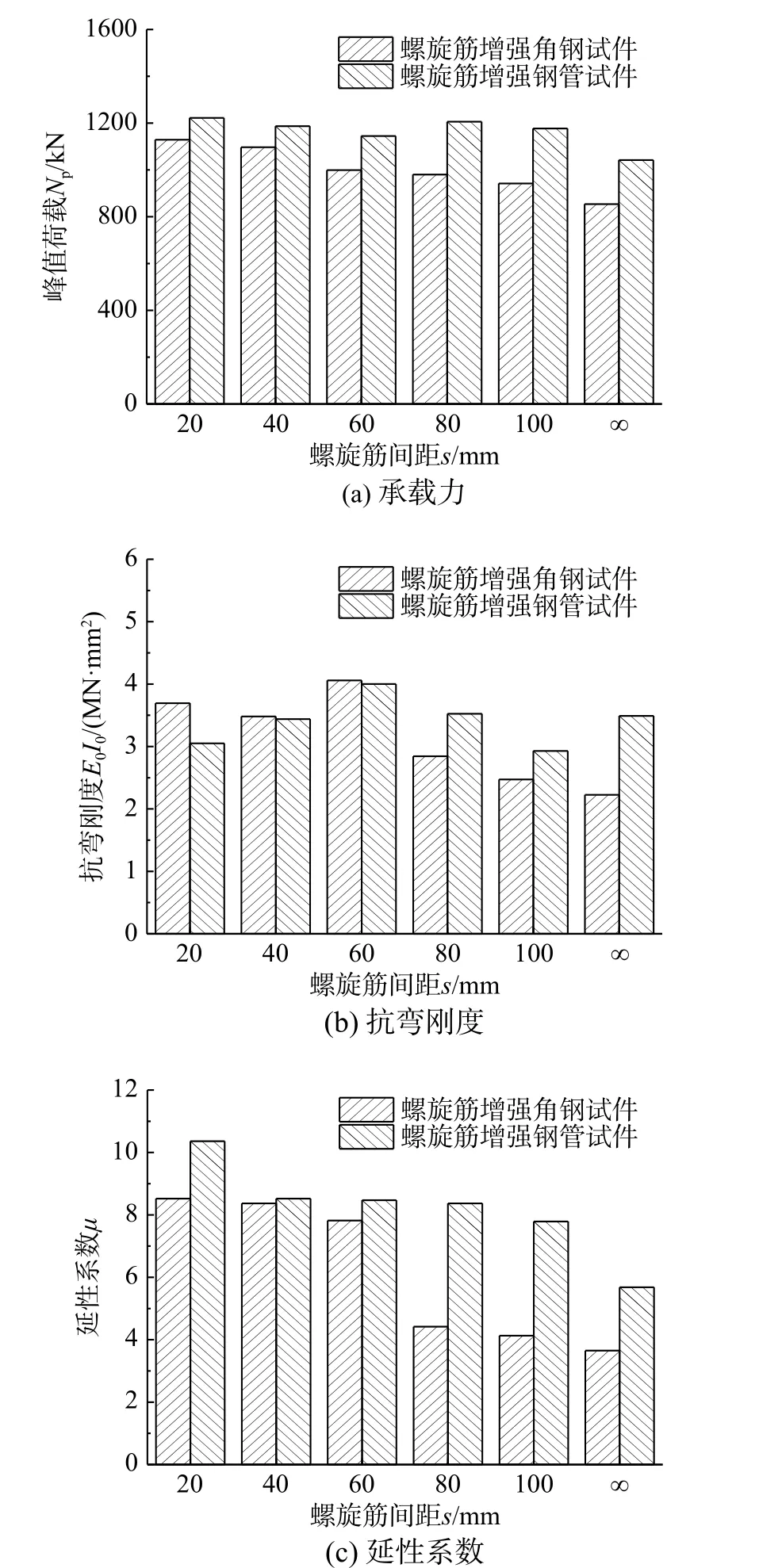
图6 螺旋筋间距对偏压性能指标的影响Fig. 6 Influence of spiral stirrup spacing on eccentric compression behavior

3.2 螺旋筋径宽比

图7 为螺旋筋径宽比对两类组合柱偏压力学性能指标的影响规律。由图7(a)可知，随着螺旋筋径宽比的增大，螺旋筋增强角钢试件的偏压承载力呈逐渐增大的变化趋势，而螺旋筋增强钢管试件的偏压承载力基本不变。对比螺旋筋径宽比为0.6 的试件，径宽比为0.9 的螺旋筋增强角钢试件的偏压承载力提高了24.6%，因此螺旋筋径宽比的增大可提升约束较差的角钢混凝土柱的偏压承载力，但对约束较强的钢管混凝土柱的偏压承载力影响较小。由图7(b)可知，随着螺旋筋径宽比的增大，试件的抗弯刚度有一定提升。对比螺旋筋径宽比为0.6 的试件，径宽比为0.9 的螺旋筋增强角钢试件和螺旋筋增强钢管试件的抗弯刚度分别增大了16.7%和24.4%，其原因是：螺旋筋径宽比的增大导致约束混凝土的面积相应增大，约束作用下混凝土受压性能的提升最终促使了试件抗弯刚度的增大。由图7(c)可知，随着螺旋筋径宽比的增大，试件的延性系数显著增大，偏压变形性能得到提升。对比螺旋筋径宽比为0.6 的试件，径宽比为0.9 的螺旋筋增强角钢试件和螺旋筋增强钢管试件的延性系数分别增大了16%和24.4%，其原因是：螺旋筋约束面积增大造成混凝土整体横向鼓胀变形能力提高。由此可见，通过增大螺旋筋的径宽比，可实现组合柱在偏压受力状态下各项力学性能指标的提升。

图7 径宽比对偏压性能指标的影响Fig. 7 Influence of diameter width ratio on eccentric compression behavior

3.3 纵向配钢率

图8 为纵向配钢率(纵筋ρv、角钢/钢管ρh)对两类组合柱偏压力学性能指标的影响规律。由图8(a)可知，纵向配钢率中，随着纵筋配钢率的增大试件偏压承载力增幅较小，在3%以内，但角钢/钢管配钢率的增大可显著提升试件的偏压承载力。对比ρh=3.16%的螺旋筋增强角钢试件，对应ρh=4.03%试件的承载力增大了16.5%；对比ρh=6.33%的螺旋筋增强钢管试件，对应ρh=8.58%试件的承载力增大了18.5%。纵筋配筋率变化范围较小可能是造成试件偏压承载力提升较小的主要原因。尽管如此，同比例增大配钢率，外部角钢/钢管对承载力的提升程度要显著大于内部纵筋，这说明增大外部约束角钢/钢管的纵向配钢率能更为有效地提升组合柱的偏压承载力。由图8(b)可知，无论是增大内部纵筋还是增大外部约束角钢/钢管的纵向配钢率均能较显著的提升试件的抗弯刚度。此外，由于钢材较高的弹性模量，即使纵向配钢率增幅很小，也能较大程度地提升试件的抗弯刚度。结合表1 来看，增大纵向配钢率对试件抗弯刚度的提升效果显著优于增大螺旋筋体积配箍率。由图8(c)可知，纵向配钢率的增大对试件的变形性能影响较小，远没有增大螺旋筋体积配箍率对试件变形性能的改善效果显著。

图8 纵向配钢率对偏压性能指标的影响Fig. 8 Influence of spiral stirrup diameter on eccentric compression behavior

3.4 偏心率

图9 为偏心率对两类组合柱偏压力学性能指标的影响规律。由图9(a)可知，随着偏心率的增大，试件的承载力呈线性下降，对比偏心率es=0.4的试件，偏心率es=1.2 的螺旋筋增强角钢试件和螺旋筋增强钢管试件的偏压承载力分别降低了51%和45.7%。因此，要合理设计此类试件的偏心率，从经济性上来说组合柱不宜用于偏心率较大的构件中。由图9(b)可知，当试件的偏心率大于0.8 时，试件的抗弯刚度显著降低。对比偏心率er=0.8 的试件，偏心率er=1.2 的螺旋筋增强角钢试件和螺旋筋增强钢管试件的抗弯刚度分别降低了34.3%和54.3%，其原因是：一方面，偏心率越大，试件的受压稳定性则越差，受二阶效应的影响就越显著；另一方面，随着偏心率的增大，试件的受压区混凝土面积逐渐减小，由于螺旋筋是通过被动约束增强混凝土的抗压性能来实现混凝土结构力学性能的改善，当混凝土受压面积减小时，螺旋筋的约束贡献被削弱。上述两方面共同引起了试件抗弯刚度的降低。由图9(c)可知，偏心率增大会导致试件的延性系数逐渐降低。对比偏心率er=0.4 的试件，偏心率er=1.2 的螺旋筋增强角钢试件和螺旋筋增强钢管试件的抗弯刚度分别降低了57.6%和36.8%，表明螺旋筋的约束效应改善变形性能的作用在偏心率较小时更易于发挥。

图9 偏心率对偏压性能指标的影响Fig. 9 Influence of eccentricity on eccentric compression behavior

4 复合约束下刚度退化分析

通过上述两类组合柱偏压力学性能影响因素对比分析可知，内置螺旋筋后形成的复合约束效应对组合柱的偏压性能产生了较大影响。为进一步明确复合约束效应对两类组合柱受力过程中刚度退化的影响规律，着重分析了不同螺旋筋设计参数下试件刚度随跨中挠度退化的差异。图10 和图11 分别为螺旋筋间距和螺旋筋径宽比对试件刚度退化过程影响曲线，图中纵坐标采用归一化刚度，即割线抗弯刚度与初始抗弯刚度的比值EI/(EI0)。

由图10 可见，未配置螺旋筋试件，即角钢混凝土和钢管混凝土试件，其受力过程中的刚度退化速率较快；内置螺旋筋后，相同退化率时组合柱试件的跨中挠度显著增大，在受力过程中的刚度退化速率显著放缓，说明形成的复合约束效应延缓了组合柱的偏压受力破坏过程，其原因是：复合约束作用对核心混凝土产生了更强的约束力，限制了混凝土的开裂及挤压流动，延缓了外部角钢/钢管的屈曲破坏。对比不同螺旋筋间距试件的刚度退化曲线发现，随着螺旋筋间距的增大，相同退化率下试件的跨中挠度减小，试件的刚度退化速率加快，说明复合约束效应的减弱将加快试件的偏压受力破坏过程。螺旋筋约束增强角钢试件刚度退化受螺旋筋间距的影响明显大于螺旋筋约束增强钢管试件，且螺旋筋间距介于1/3dc～5/9dc之间时试件的刚度退化速率变化较小。

图10 螺旋筋间距对刚度退化的影响Fig. 10 Influence of spiral stirrup spacing on stiffness degradation

由图11 可见，随着螺旋筋径宽比的增大，两类组合柱的抗弯刚度退化速率均有所减缓，其中螺旋筋径宽比介于0.6～0.7 时刚度退化速率减缓显著，介于0.7～0.9 时刚度退化速率减缓较小，说明随着螺旋筋径宽比的增大，螺旋筋维持试件抗弯刚度稳定的能力提升。出现上述规律的原因是：螺旋筋径宽比增大后复合约束区混凝土的面积随之增大，复合约束区混凝土的裂缝发展延缓、破碎程度降低[11]，进而造成试件的刚度退化速率减缓。当复合约束区混凝土面积增大到一定程度时，复合约束效力有限，对试件刚度退化的影响将不明显。

图11 螺旋筋径宽比对刚度退化的影响Fig. 11 Influence of diameter width ratio on stiffness degradation

5 承载力计算

5.1 基于偏心率折减系数的偏压承载力计算式

结合两类组合柱的偏压破坏过程及形态来看，内置螺旋筋未改变试件的破坏模式，因此本文认为内置螺旋筋不会改变角钢混凝土及钢管混凝土柱的失稳特性。基于此，根据文献[11]提出的组合柱轴压承载力计算公式，引入轴压稳定系数φl和偏心率折减系数φe，建立组合柱偏压承载力计算公式：

式中：φl为轴压稳定系数，按照GB 50936−2014《钢管混凝土结构技术规范》取值；φe为偏心率折减系数，按式(2)计算；A1、A2和A3分别为复合约束区、螺旋筋单独约束区以及角钢或钢管单独约束区的面积，按文献[9]中建立的复合约束模型计算；fc1、fc2和fc3分别为对应约束区混凝土的抗压强度；NA为外包钢材的承载力；NS为内部纵筋的承载力；er为试件的偏心率。

约束混凝土抗压强度由MANDER[3]所提出的5 参数约束混凝土强度计算模型求得：

式中：fcc为约束混凝土的抗压强度；fc0为非约束混凝土的抗压强度；fl为约束混凝土等效侧向压应力。

如图12(a)所示，根据螺旋筋约束混凝土中螺旋筋的受力平衡状态可得：

图12 轴压力下约束力分析示意图Fig. 12 Schematic diagram of constraint stress analysis under axial pressure

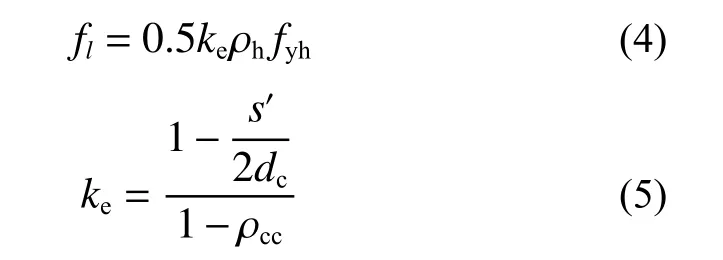
式中：ke为有效约束系数；ρh为螺旋筋体积配筋率；fyh为螺旋筋的屈服强度；s'为螺旋筋净间距；dc为螺旋筋中心约束直径；ρcc为纵筋面积与截面核心面积之比。

如图12(b)所示，根据角钢约束混凝土中角钢的受力平衡状态可得：

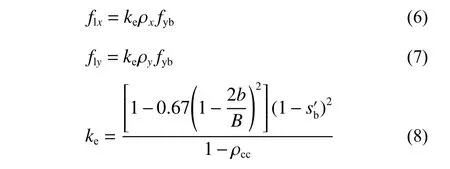
式中：ρx和ρy分别x和y方向缀板体积配钢率；fyb为缀板的屈服强度；B为截面边长；b为角钢肢长；为缀板净间距。

蔡健等[14]将钢管对混凝土的约束作用等效为有效侧压力，如图12(c)所示，根据钢管约束混凝土中钢管的受力平衡状态可得：

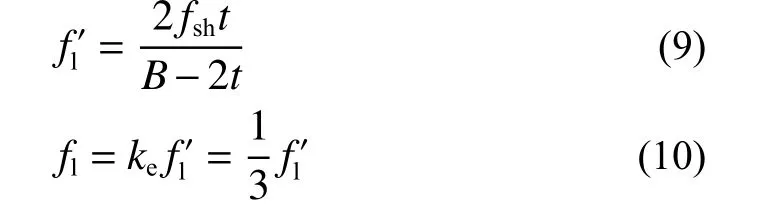
当不考虑钢管的局部屈曲时：

式中：fsh为钢管的横向拉应力；t为钢管厚度；fya为钢管的屈服强度。

外部钢材单独约束区混凝土抗压强度fc3计算时，若外部钢材为角钢，则由式(6)～式(8)算得flx和fly后，根据文献[3]中的矩形截面约束混凝土强度计算图查得；若外部钢材为方钢管，则由式(9)～式(11)算得等效侧向压应力fl后代入式(3)计算。螺旋筋单独约束区混凝土抗压强度fc2由式(4)～式(5)算得等效侧向压应力fl后代入式(3)计算。对于外部钢材与内部螺旋筋形成的复合约束区混凝土抗压强度fc1，相当于在外部钢材的约束作用基础上内部螺旋筋再次对混凝土产生约束，无论外部钢材是角钢还是方钢管，将各自算得的fc3替代fc0，再次代入式(3)～式(5)计算。

表4 列出了组合柱偏压承载力试验值与计算值的对比结果，其中Nuc1是基于偏心率折减系数的组合柱偏压承载力公式的计算值，其计算值与试验值比值的平均值为1.025，方差为0.132，变异系数为0.129。由此可见，式(1)计算值具有较大的离散度，无法准确地反映组合柱的偏压承载力，这是因为式(1)是基于轴心受压试验得到的约束混凝土模型近似分析得到的，而组合柱包含多种约束状态，近似简化的计算方法将对结果的精度产生较大影响。

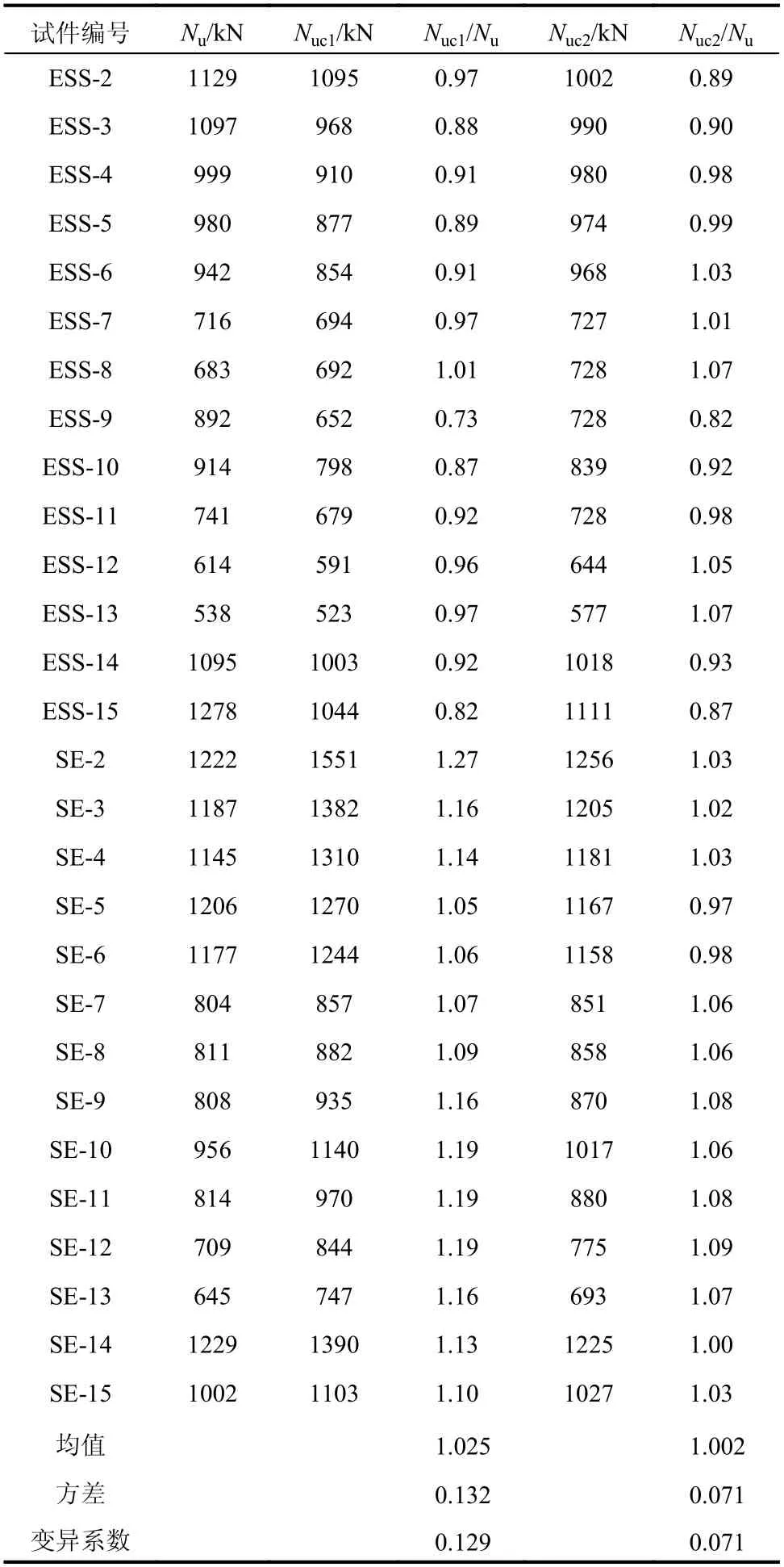
表4 试验值与计算值比较Table 4 Comparison between experimental and calculated values

5.2 基于压溃理论的偏压承载力计算式

5.2.1M-N- ϕ关系曲线

为得到精度较高的组合柱偏压承载力的计算公式，本文基于组合截面简化的弯矩-轴力-曲率(M-N- ϕ)关系曲线，根据压溃理论推导了组合柱偏压承载力的简单解析公式。为了寻求压溃理论所对应的解析解，作如下的基本假定：① 跨中截面满足平截面假定；② 钢材与混凝土之间无相对滑移；③ 构件两端为铰接，横向挠度曲线为一个正弦半波；④ 只考虑跨中截面轴力、弯矩的内外力平衡；⑤ 忽略剪力对构件变形的影响。

结合课题组前期编制的纤维模型法计算程序[15]，在保持轴向力N不变的情况下，不断改变截面曲率 ϕ，可得到截面弯矩的变化曲线。以典型试件SE2 为例，建立其不同轴力下的M- ϕ关系曲线，即得到相应的M-N- ϕ关系曲线，如图13 所示。由图可见，在不同轴力之下M- ϕ曲线基本上分3 段：弹性段、弹塑性段和塑性水平段[16]，因此简化后一定轴力下的M- ϕ关系曲线如图14 所示，其上升段基本上呈二次抛物形状。为此假定一定轴力N之下，截面的弯矩为：

图13 SE2 试件的M- ϕ曲线Fig. 13 M- ϕ curve of specimen SE2

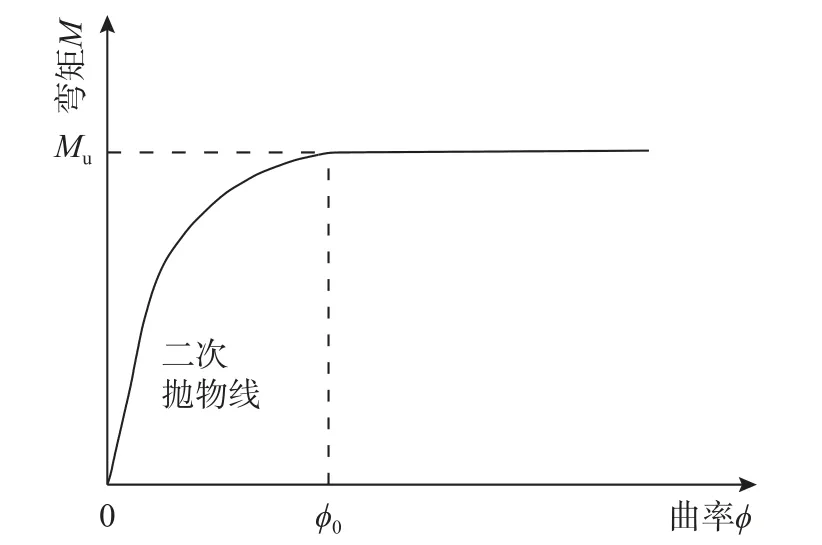
图14 简化M- ϕ曲线Fig. 14 Simplified M- ϕ curve

式中，fya和Esa分别为外部钢材(角钢或钢管)的屈服强度和弹性模量。

然后根据给定的轴力N下求出截面能承受的最大弯矩Mu，在以N为纵坐标、Mu为横坐标的直角坐标系中，就可以得到一个坐标点(Mu,N)不断改变轴力N，便可得到一系列坐标点，连接坐标点就可以得到关于给定参数的Mu-N关系曲线。以试件SE2、SE3 为例，建立对应试件的Mu-N关系曲线，如图15 所示。从安全、实用的角度出发，参照文献[17]的计算方法，简化钢-混凝土组合方柱典型的Mu-N关系曲线，如图16 所示。由图可见，类似于钢筋混凝土压弯构件，钢-混凝土组合方柱截面所能承受的最大弯矩Mmax发生在一定轴力(N>0)之下，近似的可采用分段线性化描述Mu-N曲线，如图16 虚线所示，其表达式为：

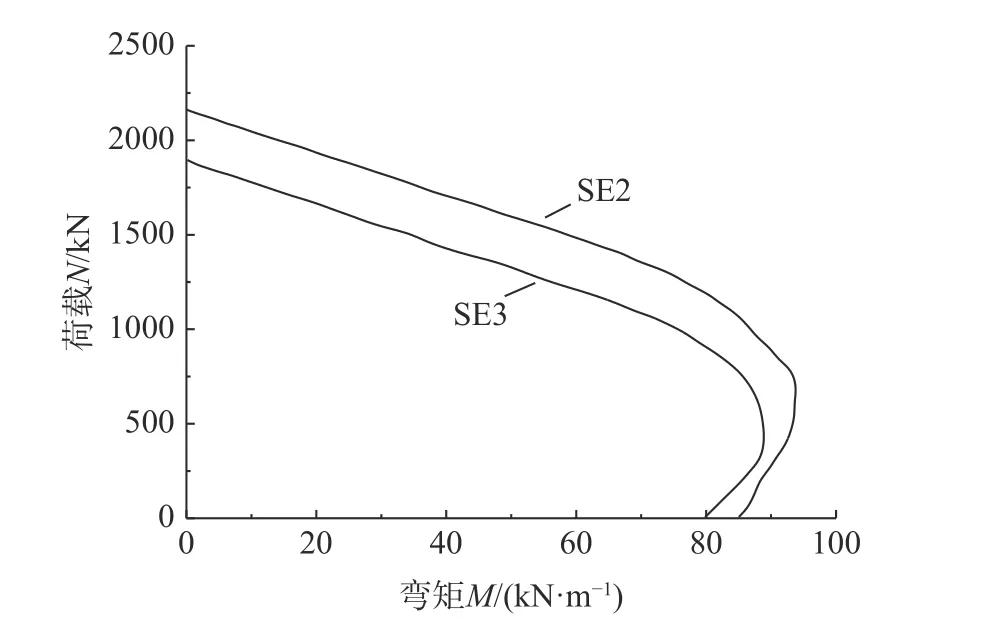
图15 典型试件的Mu-N 关系曲线Fig. 15 Mu-Nrelation curves of typical specimens

图16 M-N 曲线二段线性化Fig. 16 Linearization of M-Ncurve

式中：Nsc为构件轴压承载力；Msc为构件纯弯承载力；Nc为折线转折点对应的轴力。

5.2.2 参数确定

由以上分析可知，若已知试件的Nsc、Msc和Nc，便可确定试件的Mu-N相关曲线，同时结合式(12)求出轴力N作用下的截面弯矩，进而建立控制截面平衡方程，最终解得Nmax。因此问题的关键在于求解上述三个参数的数值。

1) 参数Nsc的确定

结合文献[11]根据复合约束模型建立的组合柱轴压承载力计算公式以及其计算精度，参数Nsc建议采用下式计算：

2) 参数Nc的确定

由图12 可知，Nc表示弯矩Msc对应的轴力值，文献[16]中建议取核心混凝土承担的轴力作为Nc。对于组合柱，参数Nc按下式计算：

3) 参数Msc的确定

Msc的物理意义为轴力为零对应的弯矩，即构件的纯弯承载力，分为以下两种情况讨论参数Msc的计算方法。

① 中和轴位于夹层混凝土中(见图17)

图17 中和轴位于夹层混凝土Fig. 17 The neutral axis in sandwich concrete

则截面弯矩为：

图18 中和轴位于螺旋筋约束混凝土Fig. 18 The neutral axis in spiral confined concrete

5.2.3 承载力解析推导

根据跨中截面内外弯矩相等，可以得到偏心力N和曲率 ϕ的关系。

外弯矩：

令：

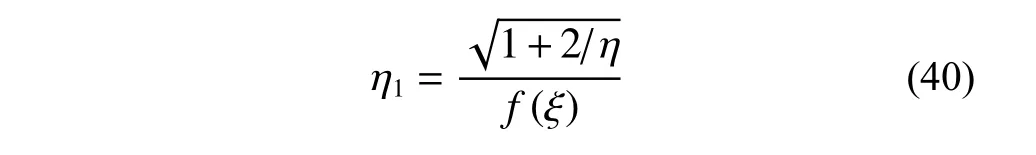
则，式(39)转化为：

结合式(14)可得偏压柱的极限荷载Nmax：

式中：e0为试件的偏心距；L为试件的高度；η、ξ 和η1为方便计算而假定的参数。表4 中Nuc2为按照压溃理论推导的组合柱偏压承载力公式的计算值，其计算值与试验值比值的平均值为1.002，方差为0.071，变异系数为0.071。由此可见，此计算方法的离散性较小、计算结果精度较高，可用于组合柱偏压承载力的计算。

6 结论

本文通过30 个螺旋筋约束增强钢-混凝土组合方柱的偏心受压试验，分析了复合约束效应对螺旋筋约束增强钢-混凝土组合方柱偏压性能的影响，讨论了复合约束下两类组合柱的刚度退化规律，并基于压溃理论推导了组合柱偏压承载力解析公式，得到主要结论如下：

(1) 组合柱偏压破坏模式分为大、小偏压破坏。内置螺旋筋后，螺旋筋增强角钢试件受压区混凝土压碎剥落时间有所延缓，且压溃程度明显减小；螺旋筋增强钢管试件受压区钢管鼓曲有所延缓，且局部鼓曲部位明显增多。

(2) 大、小偏压破坏时，受压区角钢/钢管与纵筋在峰值荷载前均发生屈服。两种破坏模式的区别在于，小偏压破坏时受拉区角钢/钢管与纵筋在峰值荷载前均未屈服，且靠近加载点螺旋筋在小偏压时屈服，大偏压时则未屈服。

(3) 内置螺旋筋可显著提升钢-混凝土柱的偏压承载力和变形性能，并一定程度上改善组合柱的抗弯刚度，上述作用效果在角钢混凝土柱中更显著。但是，过密布置螺旋筋将导致组合柱的性能提升下降，建议螺旋筋间距的取值范围为螺旋筋约束直径的2/9～4/9，其施工可行性有待足尺试验进一步验证。

(4) 增大螺旋筋径宽比可提升组合柱偏压力学性能，增大外部约束角钢/钢管纵向配钢率能显著增大组合柱的承载力和抗弯刚度，但其对变形性能的提升远小于增大螺旋筋体积配箍率。此外，偏心率的增大将显著降低组合柱的偏压力学性能。

(5) 螺旋筋间距减小及径宽比增大可减缓组合柱的刚度退化速率，且在角钢混凝土柱中更为显著。当复合约束区混凝土面积较大时，有限的约束效力对组合柱刚度退化的影响将不明显。

(6) 基于偏心率折减系数的偏压承载力计算结果精度较低，因此本文根据压溃理论推导了组合柱偏压承载力的解析公式，计算结果与试验结果吻合较好。