一种铁路漏斗车底门开闭机构受力及强度分析

陈双喜

（成都大学机械工程学院，成都 610106）

铁路漏斗车是一种散装货物（煤炭、粮食、熟料等）专用车辆，可固定编组、循环使用、定点装卸，实现装卸作业的自动化［1］。漏斗车在国外发展较早，上世纪70年代，联邦德国的燃煤电厂已经广泛采用煤炭漏斗车运煤［2］。我国于上世纪70年代开始煤炭漏斗车的研制，定型为K18，但问题较多，随后该型号漏斗车不断改进。2005年，中车太原机车车辆有限公司研制了新型KM70漏斗车。本世纪中车公 司 又开发了KM80、KM82、KM98、KM100等型号的漏斗车［3-4］。

底门开闭机构是漏斗车实现自动卸货的关键装置。我国运营的漏斗车目前采用2种底门开闭机构，即“大刀式”开闭机构和顶锁式开闭机构。这2种机构在使用过程中暴露出可靠性较差的问题，如KM18煤炭漏斗车底门自动开发故障，KM70煤炭漏斗车底门开度和锁闭不良问题［5］。目前，国内对底门开闭机构的研究较少。大连交通大学的李培行、李文成对“大刀式”底门开闭机构进行了研究，并运用ADAMS软件建立了模型，研究了该机构的运动可靠性［6-7］。

文中以目前国内煤炭漏斗车大量使用的顶锁式底门开闭机构为研究对象，从该机构运动学、力学原理角度出发，建立力学方程组及矩阵求解方法、构架强度校核方法，为该机构的设计、优化提供技术手段参考。

1 顶锁式底门开闭机构

目前我国运用的KM70、KM80等系列煤炭漏斗车均采用了顶锁式开闭机构，如图1、图2所示。该机构采用两级传动，可同时开关两侧4个（或6个）底门，具有两级锁闭装置。该种机构的锁体与底门销接触面为一圆弧面，机构开门时只需克服锁体与底门销之间的滚动摩擦力，锁体不必压缩底门即可转出，使开启底门所需的作用力较小，风动或手动开关底门时，启闭装置传动平稳、轻便、灵活。为了确保锁闭可靠，防止锁体在空车运行时振动自开，在两级传动的上、下传动轴之间，设计了一个过死点才可以开启的连杆组成，将下传动轴和锁体锁在指定的转动位置，形成了二级锁闭状态。为了实现自动快速卸车，减轻劳动强度，装有顶锁式底门开闭机构的漏斗车一般都设置了风控装置来控制底门的开闭，手动开闭机构作为一种辅助手段在无风源的情况下使用。

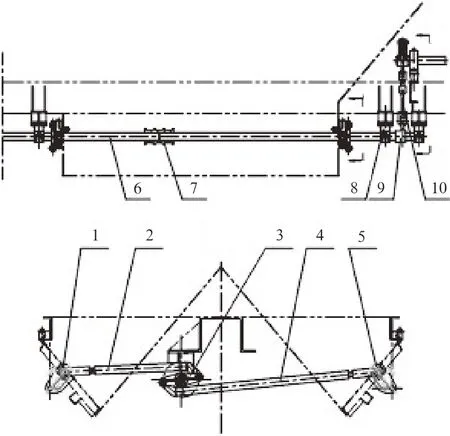
图1 顶锁式底门开闭机构示意图

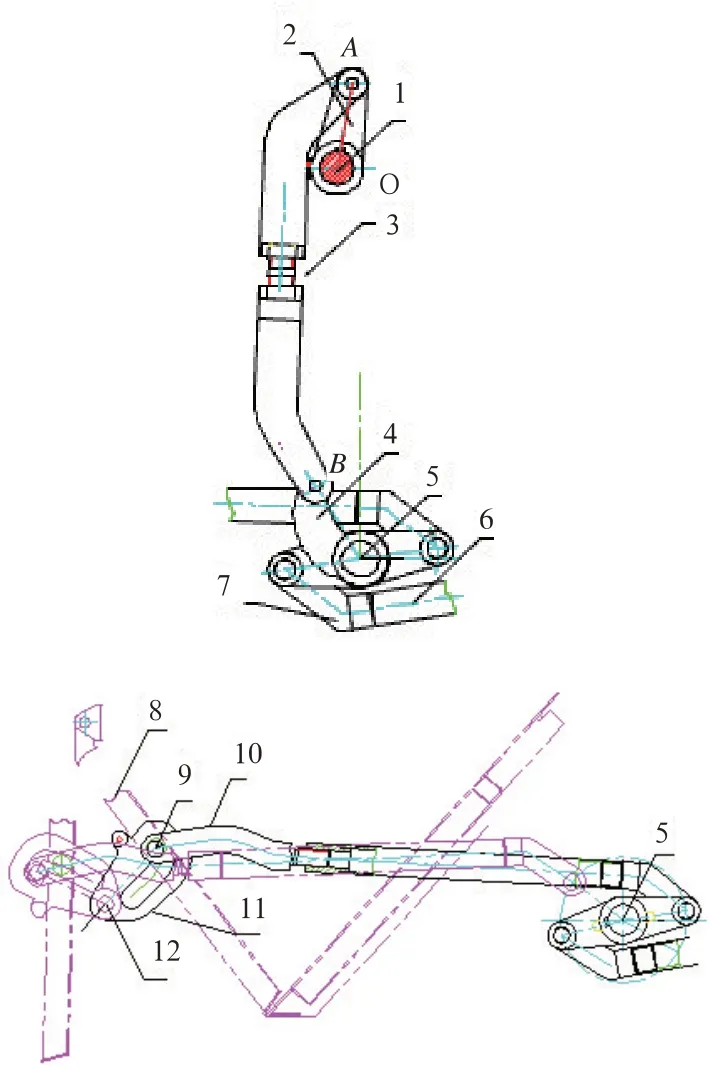
图2 上、下部传动机构组成

2 机构运动轨迹及力学模型

2.1 运动轨迹计算方法

该底门开闭机构的上部四杆传动机构如图3所示，设定下部传动轴中心为坐标原点O，则上部输入轴中心坐标点O′；O点到上曲拐铰点A距离为La；上下曲拐通过连杆为一个整体，其下端点B，A点 到B点 距 离为Lb；点B到 下 部传 动轴 距离为Lc。设杆O′A与水平轴角度为α，杆OB与水平轴角度为β，则点A、点B的坐标分别为式（1）、式（2）：

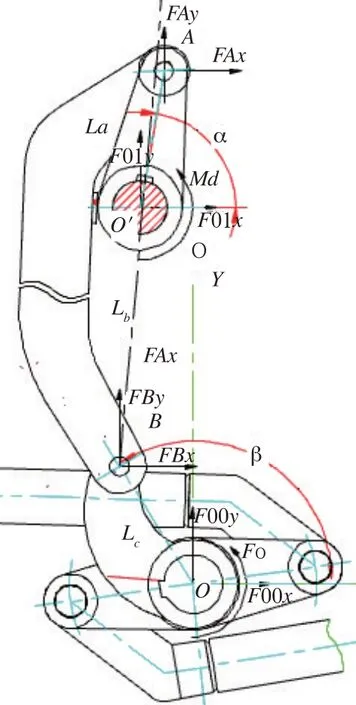
图3 上部传动机构受力图

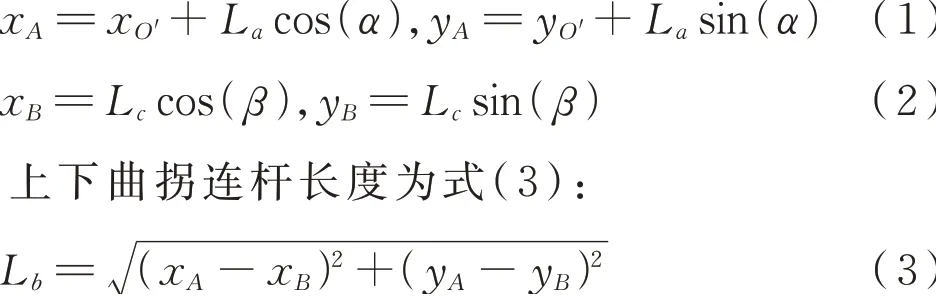
下部左侧四杆传动机构如图4、图5所示。设双联杆OC长度为Ld，与水平轴角度为γ；锁体点F到点D长度为Lf，与水平轴角度为θ，则点C、点D的坐标分别为式（4）、式（5）：

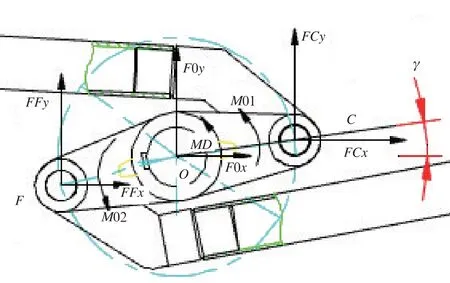
图4 下部双联杠杆尺寸与受力图

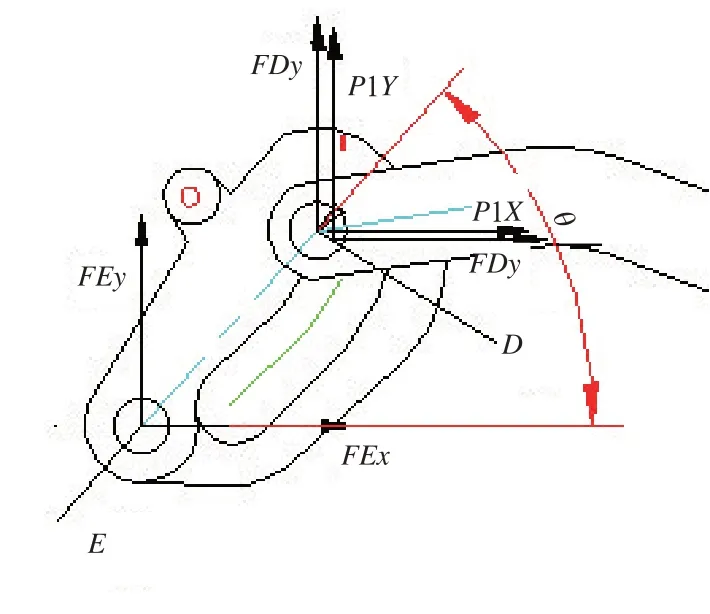
图5 左锁体受力示意图

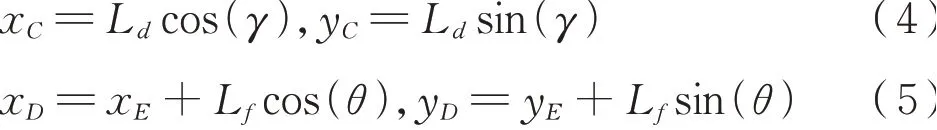
左侧底门顶杆长度为式（6）：

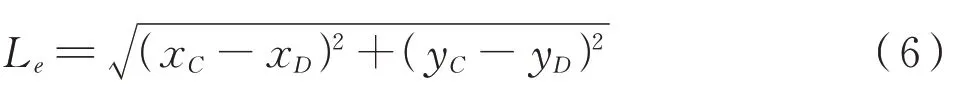
下部右侧四杆传动机构如图6所示。设双联杆OF长度为Lg=Ld；右锁体点G到点H长度为Li，与水平轴角度为φ，则点F、点G的坐标分别为

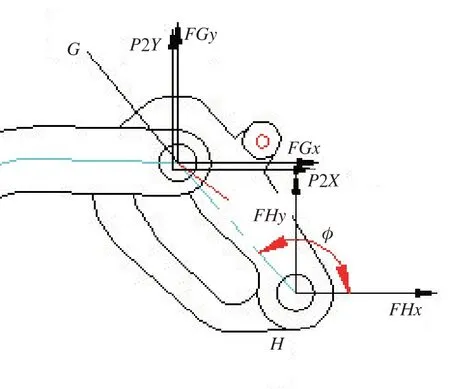
图6 右锁体受力示意图

式（7）、式（8）：

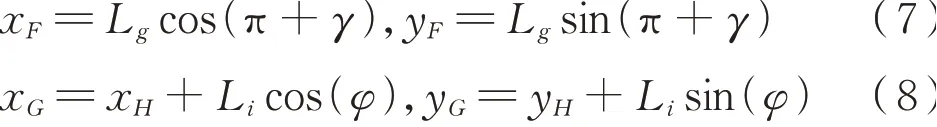
右侧底门顶杆长度为式（9）：

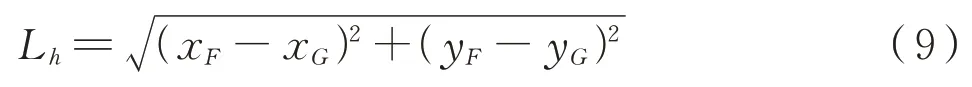
若已知上下传动轴中心O′、O坐标，锁体旋转中心E、H坐标，3个四杆机构各个杆的长度La、Lb、Ld、Le、Lf、Lg、Lh、Li。通过设定杆O′A角度α，双杠杆水平角γ，则可根据方程（3）、（6）、（9）求解出整个传动系统的运动轨迹。

2.2 力学分析模型及计算方法

根据理论力学的受力平衡和力矩平衡原理，列出下部左侧机构部件的静力学方程如下。左右锁体承受的外力为底门销的压力P1、P2，该压力方向在理论上通过锁体旋转中心。

下部传动轴联杆Ld受力方程为式（10）：

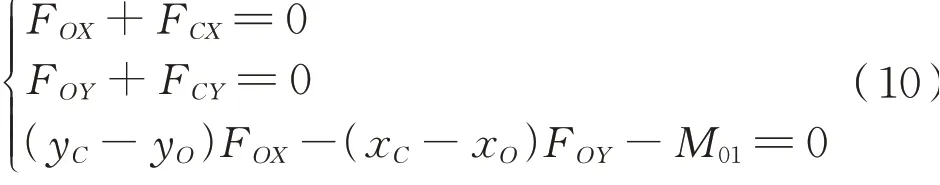
左侧顶杆Le受力方程式（11）：

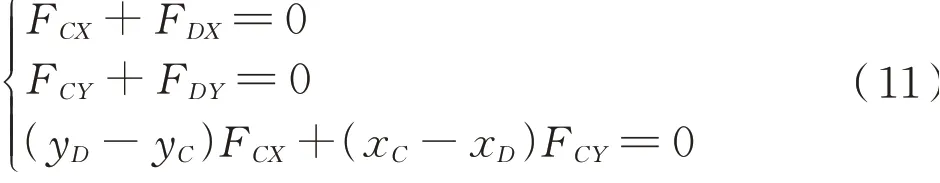
左侧底门锁体Lf受力方程式（12）：

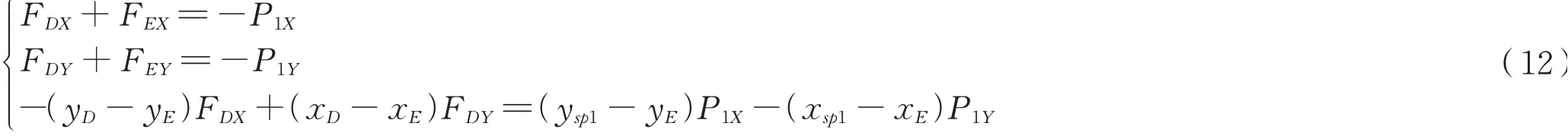
式中：xsp1、ysp1分别为底门销压力作用点位置坐标；P1X、P1Y锁体受到的外力为底门销传递的压力在x、y轴的分量。

将式（10）～式（12）方程组改为矩阵形式为式（13）：

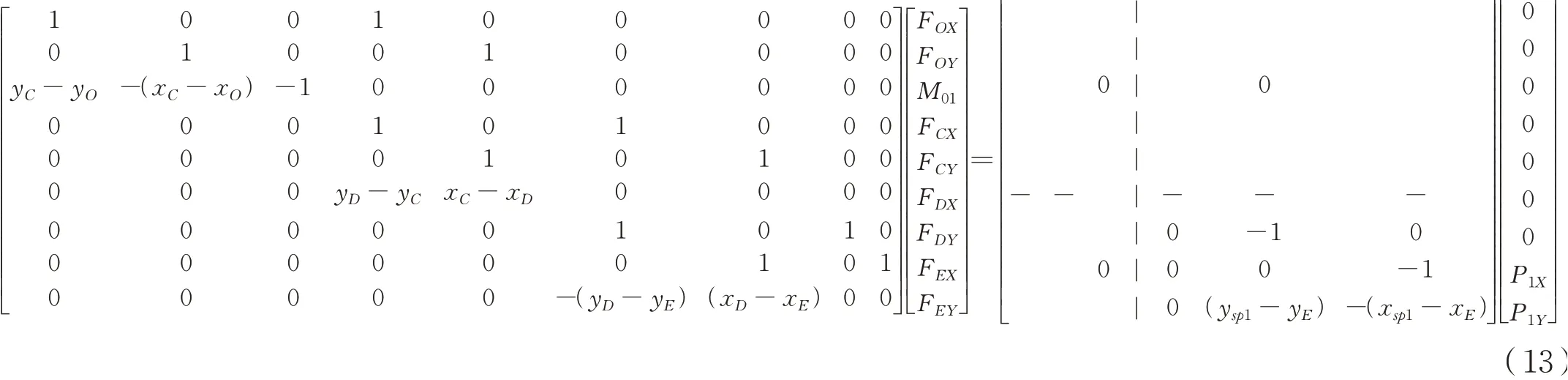
同理，上部传动机构力平衡矩阵为式（14）：

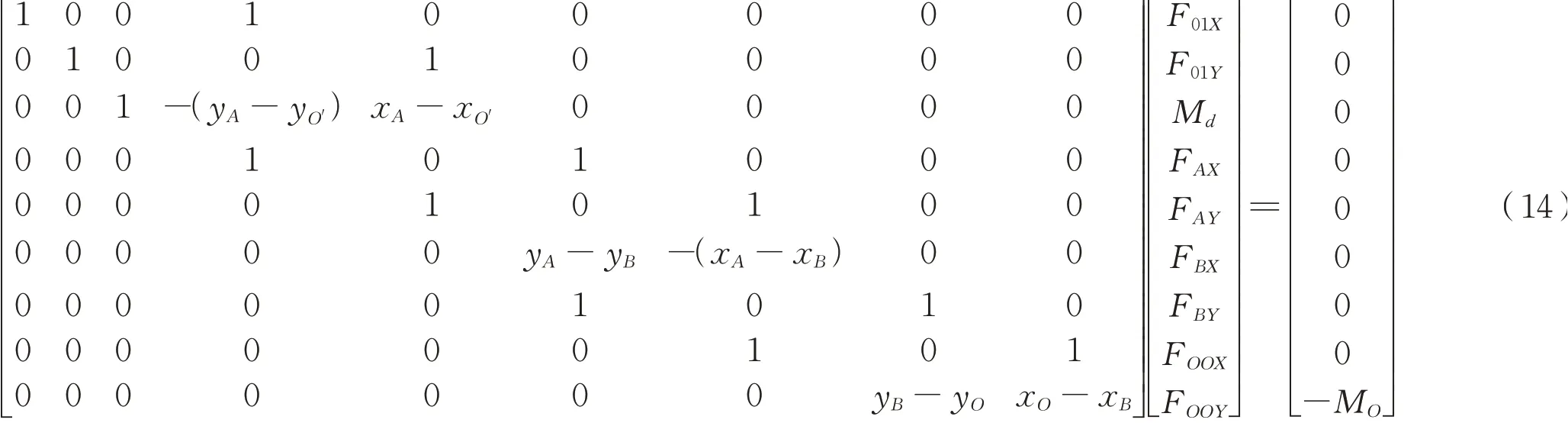
需首先求解下部矩阵式（13），得到双联杠杆受力（矩）数值，然后带入矩阵式（14）可求解输入扭矩及各个铰接点的受力。

3 算例与结果分析

已知底门开闭机构固定在车体上的铰接点O点为坐标原点；上部传动轴中心坐标：xO′=-50，yO′=2 457；左侧 锁 体 旋 转中 心坐 标：xE=-1 306，yE=505；左侧锁体旋转中心坐标：xH=-1 690，yH=50。各个连杆长度分别为：La=180 mm，Lb=847 mm，Lc=180 mm，Ld=160 mm，Le=1 348 mm，Lf=188 mm，Lg=160 mm，Lh=1 733 mm，Li=188 mm。然后根据前述第2节公式可计算运动轨迹和受力情况。对于散装颗粒货物对侧墙、端墙、漏斗脊背、底门等车体钢结构的压力计算，国内外都有相关研究［8-13］。而漏斗承受动压力的计算通常采用离散单元法建立散粒体仿真模型求解，但过于复杂且计算成本高。为简化计算，本研究根据GB 5007-2003计算底门单位面积上的法向压力。漏斗车内煤炭密度γ=13 kN/m3，内摩擦角α=53°，摩擦系数0.35，漏斗底部距车顶高度s=3.5 m，动态放大系数γq=1.3，则底门受到法向压力计算公式为式（16）：

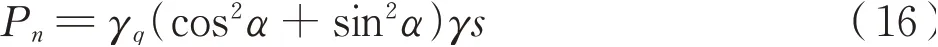
底门长度2.8 m，宽度0.8 m，可计算出底门销作用在锁体上的力P1、P2。

3.1 运动轨迹

设定驱动杆La的初始角度α=80°，下部传动轴双杠杆初始角度γ=8°，则下曲拐Lc的角度β、左锁体Lf转动角度θ、左锁体Li转动角度Φ随上曲柄La角度α的变化曲线如图7所示。底门完全打开 过 程 中，α从80°增 加 到241°；β角 从122°增 加 到262°，γ角从8°增加到148°，θ角从48°增加到160°，Φ角从132°变化到28°。由于下曲柄和双联杠杆在连接在下部传动轴上，因此β角和γ角的变化趋势相同，且变化量是一样的。左侧锁体θ角增加的同时右侧锁体Φ角减小，直到底门完全打开。

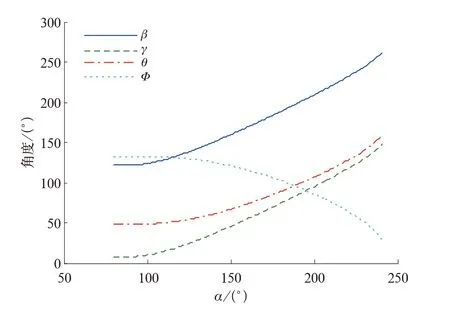
图7 机构部件角度变化曲线

3.2 受力分析

底门开闭机构在缓慢开启过程中，机构的输入扭矩与阻力矩随上曲拐角度变化如图8所示。当角度小于87°时，由于机构的自锁功能，需要初始启动力矩才能转动曲柄。随着角度增大，所需的启动力矩逐渐减小。当上曲拐La角度α大于86°后，所需扭矩小于零，表示整个机构不再需要外力矩即可完成底门打开运动。可以看出，只需要转动上曲拐7°，即可克服该机构锁死状态时刻的阻力矩，打开车体的底门。还可以看出，漏斗车满载工况下底门承受阻力矩很大，但打开底门所需的驱动力矩比阻力矩要小的多。

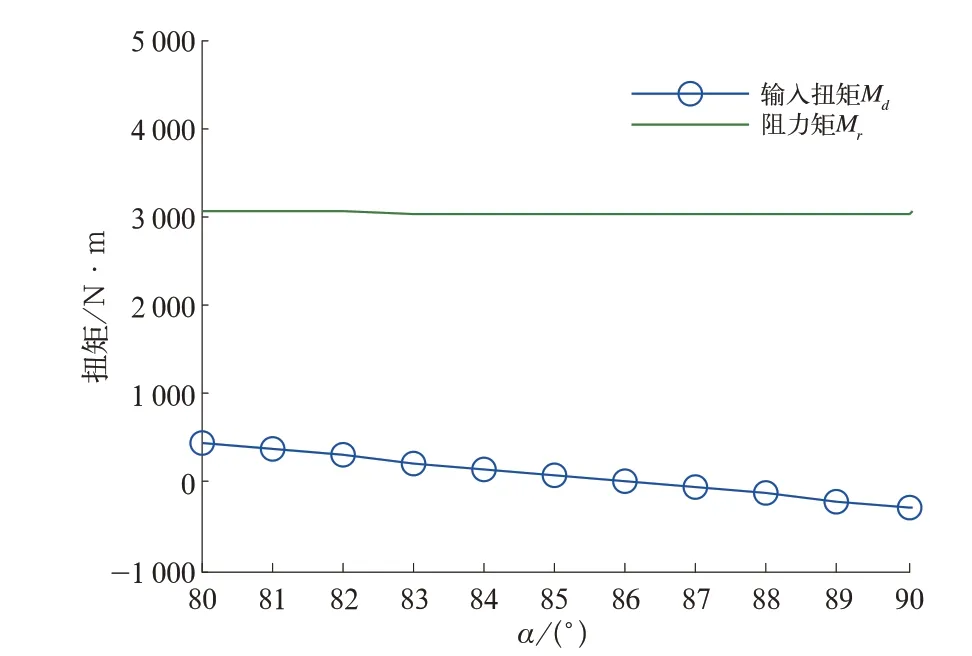
图8 机构阻力矩与驱动力矩曲线

典型的机构构件受力绝对值随上曲拐角度变化曲线如图9所示。上曲拐La、顶杆Le和顶杆Lh受力随角度α增加而增大，上曲拐受力甚至大于下部的左右两侧的顶杆。

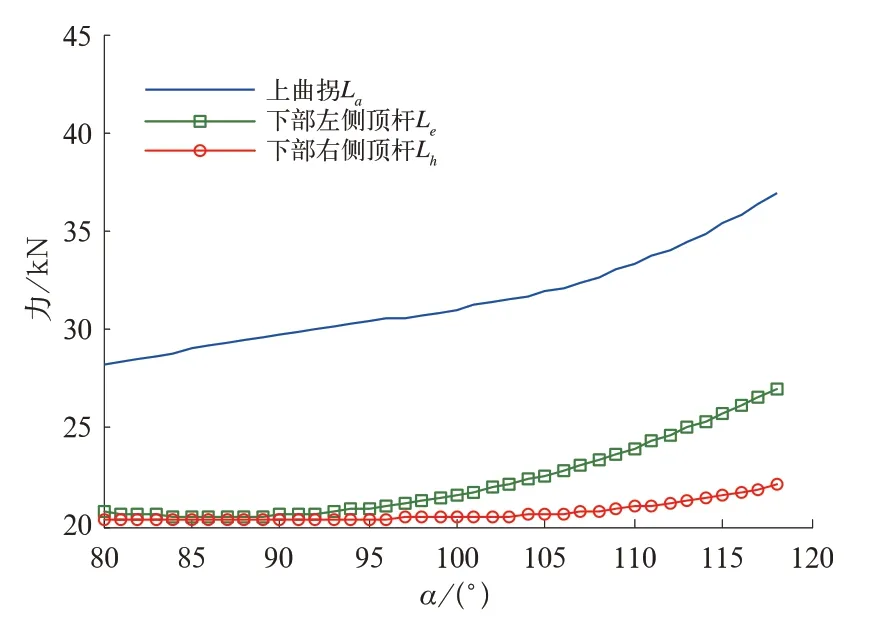
图9 机构部件受力变化曲线

3.3 结构强度分析

常用的机构强度分析方法有2种：一是在有限元软件里面建立完整的机构模型；二是在刚体动力学软件中建立刚柔耦合动力学模型［14-15］。第一种方法对计算机硬件要求较高，如果机构复杂，模型网格数量非常巨大。第二种方法只对关心的部件建立有限元模型，其他部件假定为刚体，能大幅降低计算成本。本研究采用另外一种更为简便的方法：建立单个零部件的有限元模型，从力学方程组得到机构铰接点的支反力（矩），根据作用力与反作用力原理，将该支反力（矩）作为载荷条件输入模型。计算结果与前2种方法一致。典型的应力计算结果如图10所示，在初始最大扭矩作用下，下曲拐Lc最大应力83.8 MPa，位置在曲拐根部。

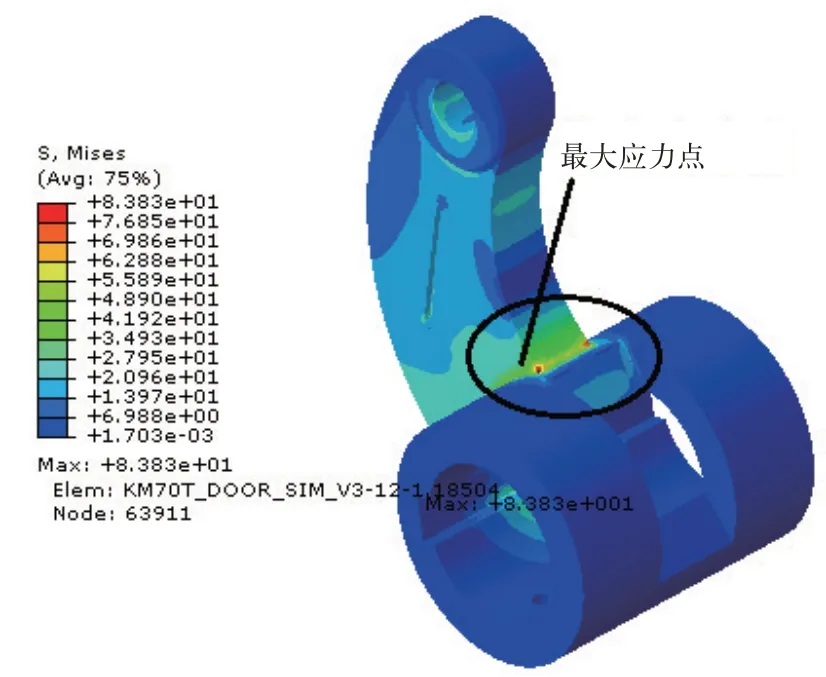
图10 下曲拐Lc应力云图

整个机构各个部件的应力和安全系数见表1，可以看出曲拐连杆Lb和下部左侧顶杆Le应力超过180 MPa，安全系数低，分别为1.2、1.3，是整个机构的薄弱环节。

表1 机构部件应力及安全系数

4 结论

本研究对铁路漏斗车顶锁式底门开闭机构各部件的空间几何关系进行分析，建立关键铰接点运动轨迹函数方程组；求解方程组，获得曲拐、双联杠杆、底部传动轴、锁体等关键部件的转动角度、铰点运动轨迹。根据理论力学的受力平衡和力矩平衡原理，列出下部左侧、右侧传动机构和上部传动机构的力学方程组。首先求解下部左、右两侧机构力学方程矩阵，得到双联杠杆受力（矩），然后带入上部传动机构力学方程矩阵，得到输入扭矩及各个铰接点的受力随转动角度变化情况。建立关键零部件的有限元模型，根据作用力与反作用力原理，将从力学方程组得到的铰接点支反力（矩）作为载荷条件，计算得到关键部件的应力、应变及安全系数。通过对典型算例分析，得到如下结论：

（1）给出的计算方法能有效地对底门开闭机构进行运动学、力学分析，可用于指导顶锁式底门开闭机构的设计。

（2）曲拐连杆和下部顶杆是顶锁式底门开闭机构的强度薄弱点，结构设计需重点关注，可有针对性地对该机构薄弱点进行结构优化和改进。