基于半监督学习网络的雷达有源干扰识别

高泽鋆，曹 菲，何 川，冯晓伟，许剑锋，秦建强

(火箭军工程大学，陕西 西安 710025)

0 引言

雷达利用目标回波感知目标的距离、速度和方位等信息[1]。目标回波不仅携带目标信息，而且包含各类杂波以及人为制造的干扰。其中，欺骗式干扰和转发式干扰因具有与目标回波较为相似的时域和频域特征，在接收端形成大量假目标，对雷达回波信号识别造成严重干扰[2]，尤其是基于数字射频存储器(digital radio frequency memory，DRFM)技术产生的间歇采样转发式干扰可在目标上实现搭载，其形成的多点源主瓣干扰，对现代雷达构成严重威胁[3]。雷达抗干扰的基本思路是“辨识-剔除”[4]，其中，“辨识”是抗干扰的前提和关键。目前，国内外学者和机构针对雷达干扰信号智能识别进行了广泛深入研究，主要基于有监督学习网络对信号进行特征提取和特征融合，在此基础上实现信号调制类型识别[5-8]。但在电子对抗中，雷达有源干扰信号样本难以获得且标签成本昂贵，导致基于有监督学习网络的雷达有源干扰识别技术应用受到极大限制。

近年来，半监督学习(semi-superuised learning, SSL)由于可利用未标记的数据提高模型性能而得到广泛关注和研究[9]。MixMatch算法使用模型的预测为未标记示例生成一个标签“猜测”，并使用MixUp混合标记和未标记的数据，在许多数据集和不同标记数量的情况下获得了良好的效果[10]。无监督数据增强方法(unpupervised data augmentation, UDA)通过使用先进的数据增强方法(如RandAugment和back translation)代替简单的去噪操作，在相同的一致性训练框架下对6种语言和3种视觉任务进行了实质性的改进[11]。ReMixMatch通过引入分布对齐和增强锚定两种新技术，改进了MixMatch半监督学习算法[12]。FixMatch算法通过对所有类使用一个预定义的常量阈值来选择对训练有贡献的未标记数据，在各种标准的半监督学习基准中实现了最先进的性能[13]。FlexMatch算法提出了课程伪标注(curriculum pseudo labeling， CPL)方法，其核心是在每个时间步中灵活地调整不同类的阈值，以便传递信息丰富的未标记数据及其伪标记，将CPL应用于FixMatch后的算法称为FlexMatch，在各种SSL基准上实现了最先进的性能[14]。然而，在雷达有源干扰识别中，SSL的应用研究鲜有报道。

针对上述问题，为提升具有少量标签的雷达有源干扰识别性能，提出一种基于SSL网络的雷达有源干扰识别方法。

1 雷达有源干扰信号建模与时频分析

按照干扰信号的产生特点，有源干扰可分为噪声类的主动压制性干扰、模拟回波的欺骗式干扰和基于DRFM技术的转发式干扰三种类型[15]。本节基于伪随机码体制雷达，进行目标回波和有源干扰信号建模，为后续干扰信号识别提供理论依据。

1.1 雷达回波和有源干扰信号模型与时频分析方法

1.1.1雷达回波信号[16]

假设射频振荡源的输出信号为

Scw(t)=Acwcos(ω0t)，

(1)

式(1)中，ω0为载波角频率，Acw表示射频信号的幅值。

脉冲调相器输出信号为

(2)

式(2)中，

(3)

式(3)中，Ap为射频信号经调相后的幅值；P(t)赋值0或1，与伪随机码的状态0和1一一对应；TR为调制脉冲周期；τA为调制脉冲宽度。

发射信号为

(4)

式(4)中，As为发射信号幅值，其值为Ap经过发射机增益后的值。

目标反射的部分回波信号Sr(t)到达接收天线，被接收到的目标回波为

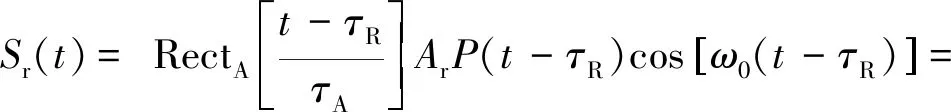
(5)

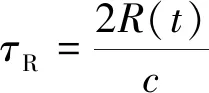
1.1.2压制性干扰

压制性干扰使用噪声或类似噪声的干扰信号遮盖有用信号，通过降低雷达接收机信噪比使其难以发现目标。按照干扰产生方式不同，压制性干扰可分为射频噪声干扰、噪声调幅干扰、噪声调频干扰和噪声调相干扰等，本节主要讨论噪声调幅干扰和噪声调频干扰。

1)噪声调幅干扰

噪声调幅干扰利用噪声对射频信号幅值进行调制，其表达式为[17]

JA(t)=[A0+n(t)]cosωjt，

(6)

式(6)中，A0为载波振幅；ωj为载波角频率；n(t)为均值为0，方差为σ2的广义平稳噪声。

2)噪声调频干扰

噪声调频干扰利用噪声对射频信号频率进行调制，可表示为[17]

(7)

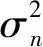
1.1.3欺骗式干扰

欺骗式干扰作用于接收机的处理过程，干扰方通过发送模拟目标回波，在雷达的接收端和信号处理系统中产生假目标，诱导其检测和跟踪过程偏离真实目标。干扰方通过改变距离时延可实现距离欺骗干扰，或者调整多普勒频移可实现速度欺骗干扰[17]。

1)距离欺骗干扰

假设发射信号如式(4)所示为Ss(t)，干扰机接收到发射信号后，首先对其特征参数进行解调提取，然后模拟产生与目标回波相同或者相似的干扰信号为Sj(t)[16-17]，则Sj(t)表达式为

(8)

式(8)中，Aj为接收机接收的干扰信号幅度，τj为干扰总延迟(包含干扰机固有延时和干扰方设置的干扰延迟)，P(t)为与目标信号相同的伪随机码信号。

2)速度欺骗干扰

雷达发射信号跟踪移动目标时，干扰机转发的模拟回波与目标回波的多普勒频率ωd之间相差一个或多个干扰信号频移，诱导雷达系统检测和跟踪过程偏离目标。模拟目标回波信号可表示为[16, 18]

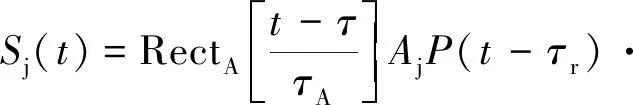
(9)

式(9)中，ωdj为干扰信号产生的频移。

1.1.4间歇采样转发式干扰

基于DRFM技术的间歇采样转发式干扰通过对接收的射频信号进行采样、存储、处理、重构和转发，能够与雷达发射信号保持部分相参性，因此干扰信号经过脉冲压缩后，能够获得一定的处理增益。典型间歇采样转发式干扰有直接、重复和循环转发三种方式，本节以直接和重复转发两种方式为例展开讨论。

1)间歇采样直接转发式干扰

间歇采样直接转发式干扰可表示为[3, 19-20]

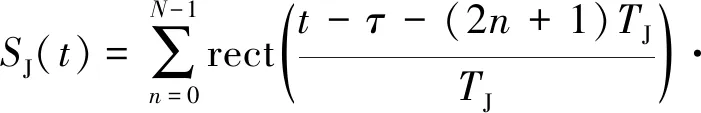
(10)

式(10)中，rect(·)波形门函数，N为干扰切片个数，TJ为干扰切片宽度，Kr为发射信号调频率，τ为干扰机到雷达距离引入的延时。

2)间歇采样重复转发式干扰

间歇采样重复转发式干扰可表示为[3, 19-20]

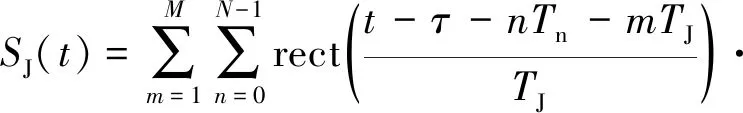
(11)

式(11)中，M为每个切片被转发的次数，Tn=(M+1)·TJ为干扰机截获信号的时间间隔。

1.1.5时频分析方法

时频分析基于变换域对信号进行预处理，其提取的高维特征能够较好地表征不同调制类型信号[21-22]。针对非线性、非平稳的雷达信号，魏格纳分布(Wigner-ville distribution，WVD)是对其进行时频域分析的有效方法。

设混合信号u(t)满足

u(t)=au1(t)+bu2(t)，

(12)

式(12)中，u(t)、u1(t)和u2(t)的时频形式分别为P(t,f)、P1(t,f)和P2(t,f)。其线性时频关系满足

P(t,f)=aP1(t,f)+bP2(t,f)。

(13)

对应其非线性时频关系可以表示为[21]

P(t,f)=a|P1(t,f)|2+b|P2(t,f)|2+
2Re[ab|P12(t,f)|2]，

(14)

式(14)中，P12(t,f)代表混合信号u(t)的交叉项。

常用的时频分布有伪魏格纳分布(pseudo Wigner-ville distribution, PWVD)、平滑伪魏格纳分布(smoothed pseudo Wigner-ville distribution, SPWVD)以及Choi-Williams分布(Choi-Williams distribution, CWD)等[22]。其中，PWVD的时频聚集性较强且交叉项抑制效果较好，同时其计算也较为简便，故本课题采用该分布进行雷达有源干扰信号特征提取。

1.2 参数设置与仿真

本节基于Matlab仿真，得到经混频处理后的中频干扰信号时域波形图、频谱图和时频分布图，并给出对应相关器[23]的输出结果。

1.2.1伪随机码脉冲多普勒雷达回波仿真

参数设置：设伪随机码码元宽度Tc=50 ns，码长P=31，故脉冲宽度T=1 μs，脉冲重复周期TR=5 μs，载波频率f0=220 MHz，弹目距离Rt=60 m，信噪比为10 dB。在不存在干扰信号时，目标回波信号处理后得到中频信号，与本振信号在相关后输出，并计算此时的目标多普勒频率fd=656 Hz。

目标回波仿真如图1、图2所示。

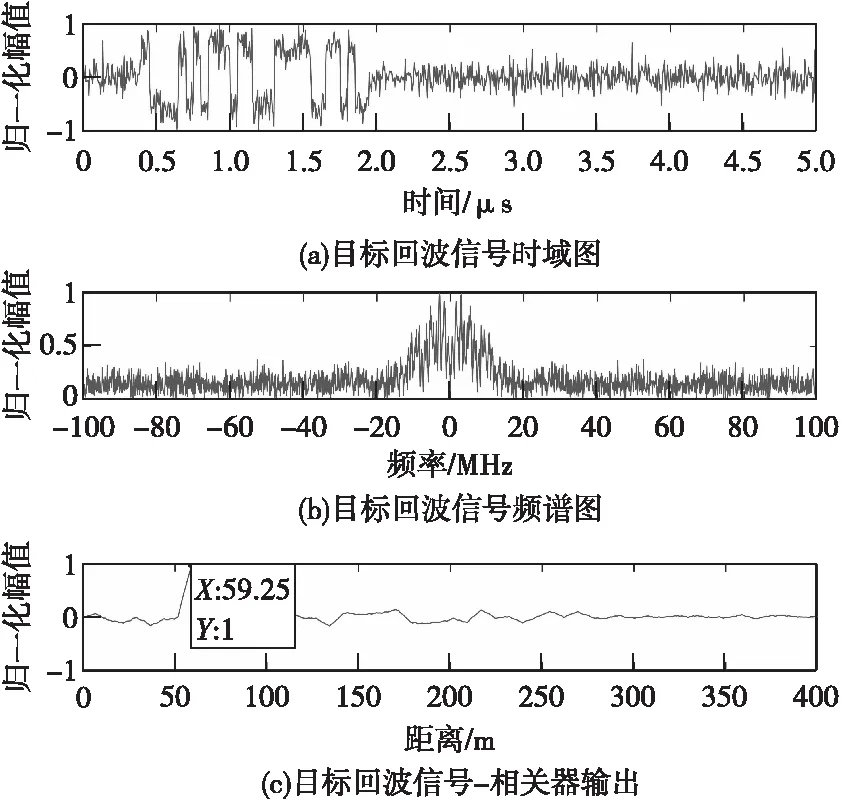
图 1 目标回波信号时域图、频谱图和相关器输出Fig.1 Time domain plot, spectrogram and correlator output

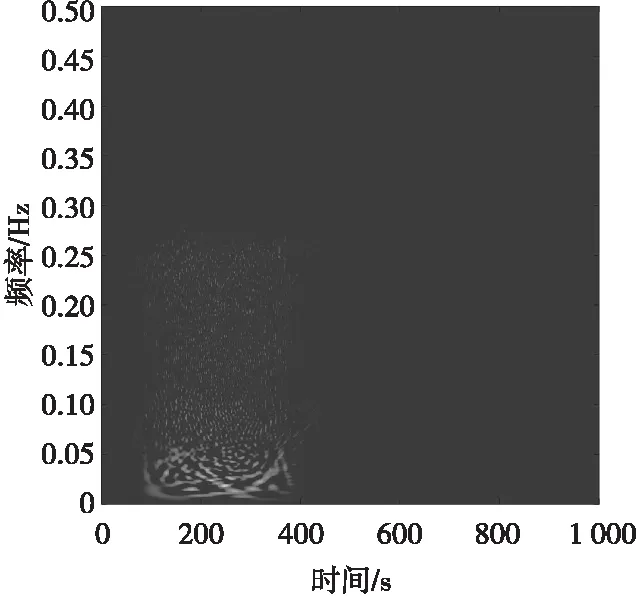
图2 目标回波信号时频分布图Fig.2 Time-frequency distribution diagram

从图1(c)可以看出，在不存在任何干扰的情况，通过相关器波形可以精确地判断出此时的弹目距离。

1.2.2雷达有源干扰仿真

1)压制性干扰仿真

参数设置：设干信比为10 dB，调频斜率106，调相斜率为3，其余参数与1.2.1节所示保持不变，信号带宽为20 MHz，为实现压制式干扰，压制信号带宽为80 MHz。

噪声调幅干扰仿真如图3、图4所示。

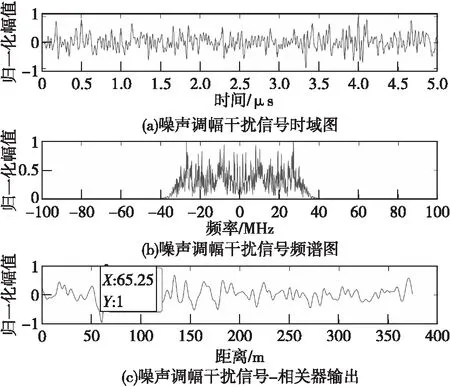
图3 噪声调幅干扰信号时域图、频谱图和相关器输出Fig.3 Time domain plot, spectrogram and correlator output

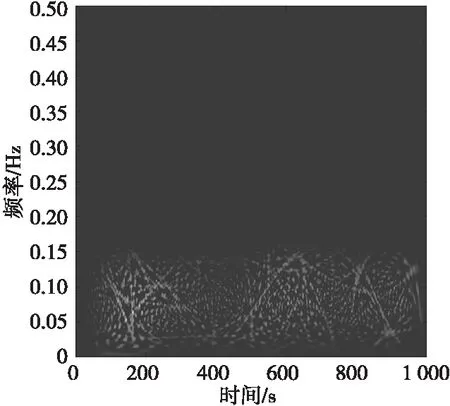
图4 噪声调幅干扰信号时频分布图Fig.4 Time-frequency distribution diagram

噪声调频干扰仿真如图5、图6所示。

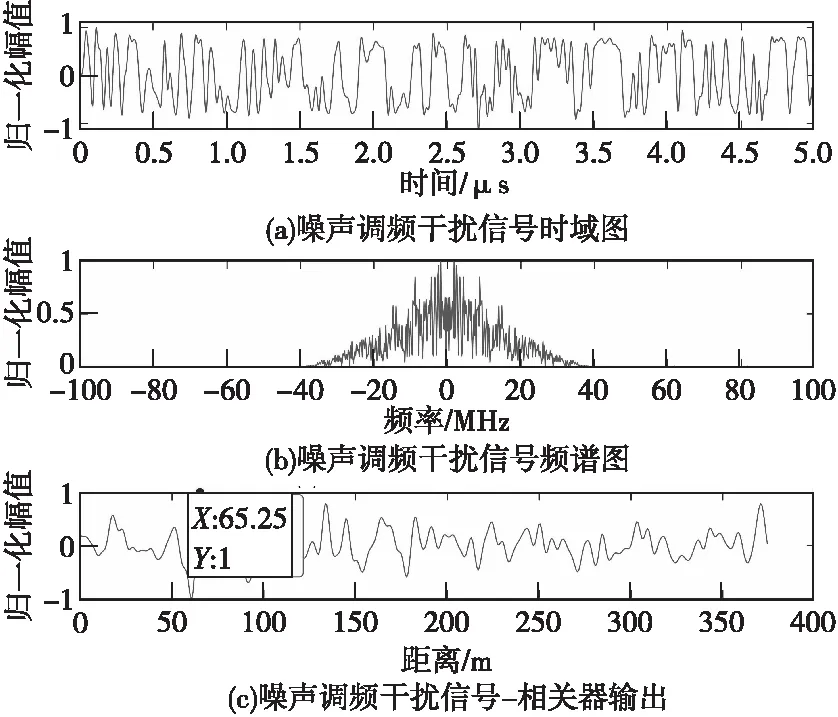
图5 噪声调频干扰信号时域图、频谱图和相关器输出Fig.5 Time domain plot, spectrogram and correlator output

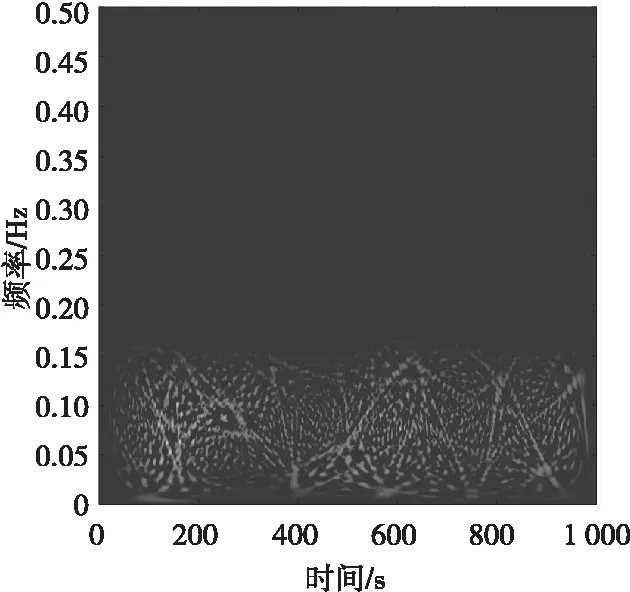
图6 噪声调频干扰信号时频分布图Fig.6 Time-frequency distribution diagram

压制性干扰需要较大的功率。从图3(c)和图5(c)可以看出，随着干信比的增大，干扰信号成功实现了对目标信号的干扰压制。两者与目标回波在时域的特征相似度较高，在频域的特征差异较为明显，而其时频分布特征存在一定的相似性。

2)欺骗式干扰仿真

参数设置：干信比为5 dB，欺骗距离Rj=20 m，其余参数如1.2.1节所示保持不变。对于速度欺骗干扰，可通过相位调制达到干扰效果。

距离欺骗干扰仿真如图7、图8所示。

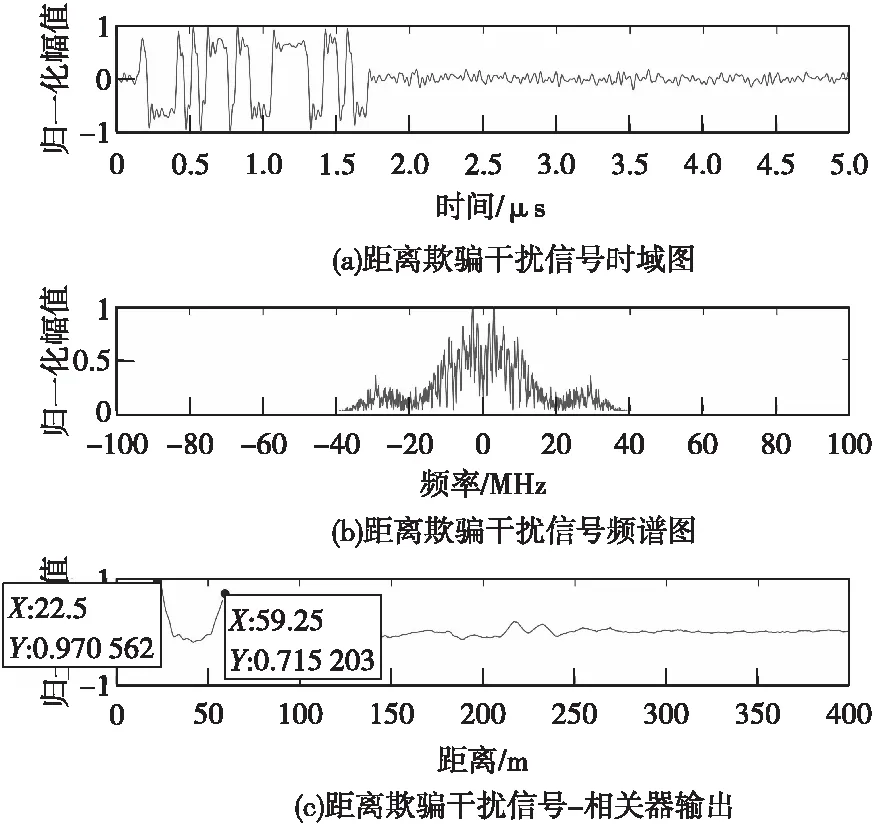
图7 距离欺骗干扰信号时域图、频谱图和相关器输出Fig.7 Time domain plot, spectrogramand correlator output

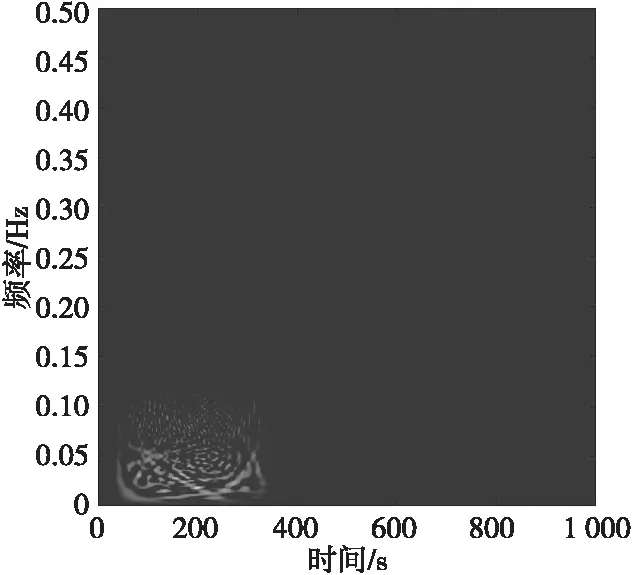
图8 距离欺骗干扰信号时频分布图Fig.8 Time-frequency distribution diagram

速度欺骗干扰仿真如图9、图10所示。

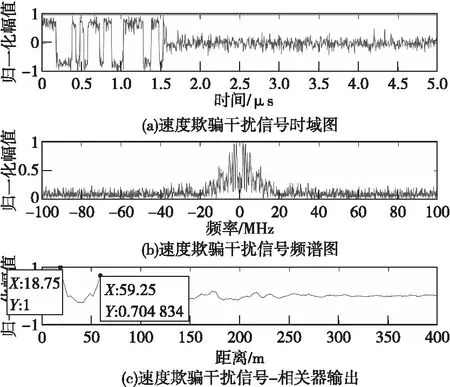
图9 速度欺骗干扰信号时域图、频谱图和相关器输出Fig.9 Time-domain plots, spectrograms, and correlator outputs

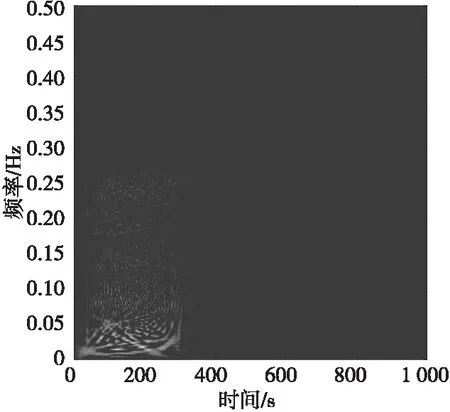
图10 速度欺骗干扰信号时频分布图Fig.10 Time-frequency distribution

可见欺骗式干扰能够在较小干扰功率条件下达到良好的干扰效果，且在时域和频域上都与目标具有相似的特征。但是，两者之间及其与目标回波的时频分布特征差异较为明显。

3)间歇采样转发式干扰仿真

参数设置：干信比为13 dB，欺骗距离Rj=20 m，其余参数与1.2.1节所示保持不变。

间歇采样直接转发式干扰仿真如图11、图12所示。

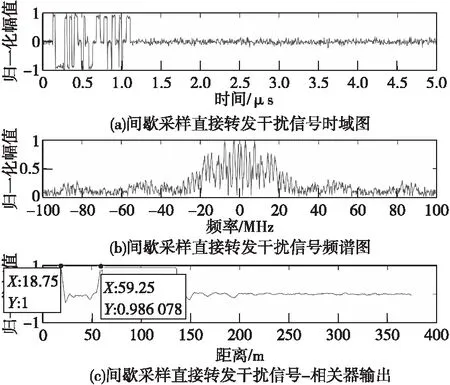
图11 间歇采样直接转发干扰信号时域图、频谱图和相关器输出Fig.11 Time-domain plot, spectrogram and correlator output

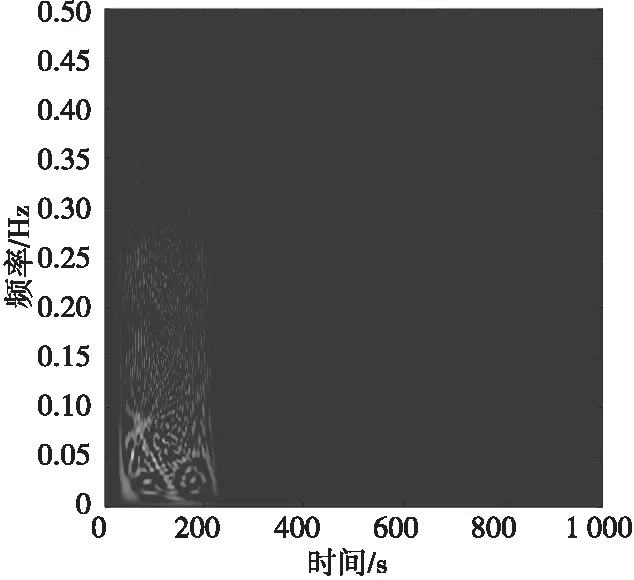
图12 间歇采样直接转发干扰信号时频分布图Fig.12 Time-frequency distribution

间歇采样重复转发式干扰仿真如图13、图14所示。

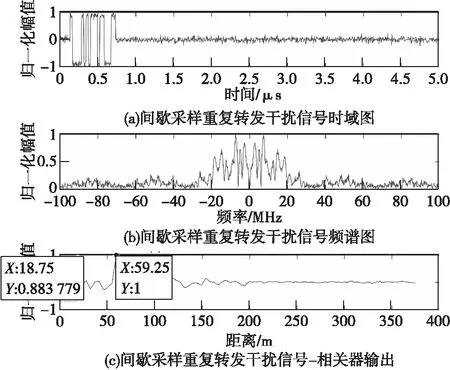
图13 间歇采样重复转发干扰信号时域图、频谱图和相关器输出Fig.13 Time-domain plot, spectrogram and correlator output

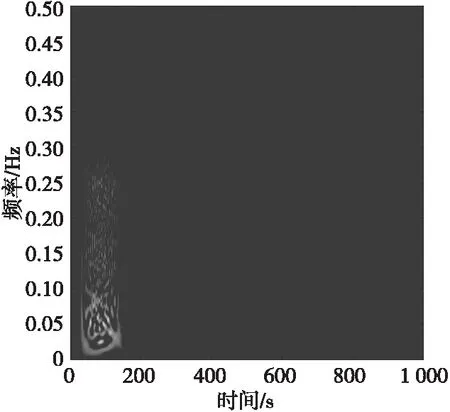
图14 间歇采样重复转发干扰信号时频分布图Fig.14 Time-frequency distribution

可见间歇采样转发式干扰能够以较小的干扰功率达到良好的干扰效果。两种转发式干扰与目标回波的时域和频域特征相似度较高，但三者时频分布特征差异较为明显。

2 基于半监督学习网络的雷达有源干扰识别

2.1 数据集构建

根据上述仿真分析和不同调制类型干扰在时频域的差异性特征，采用时频分布作为干扰信号特征提取的主要方法。本节运用Matlab仿真生成雷达回波和干扰信号数据后，基于PWVD变换提取信号高维特征，然后运用Python按照CIFAR-10数据集的结构构建雷达有源干扰数据集。该数据集中包含7种信号，每一类型包含6 000个样本，具体结构如表1所示。

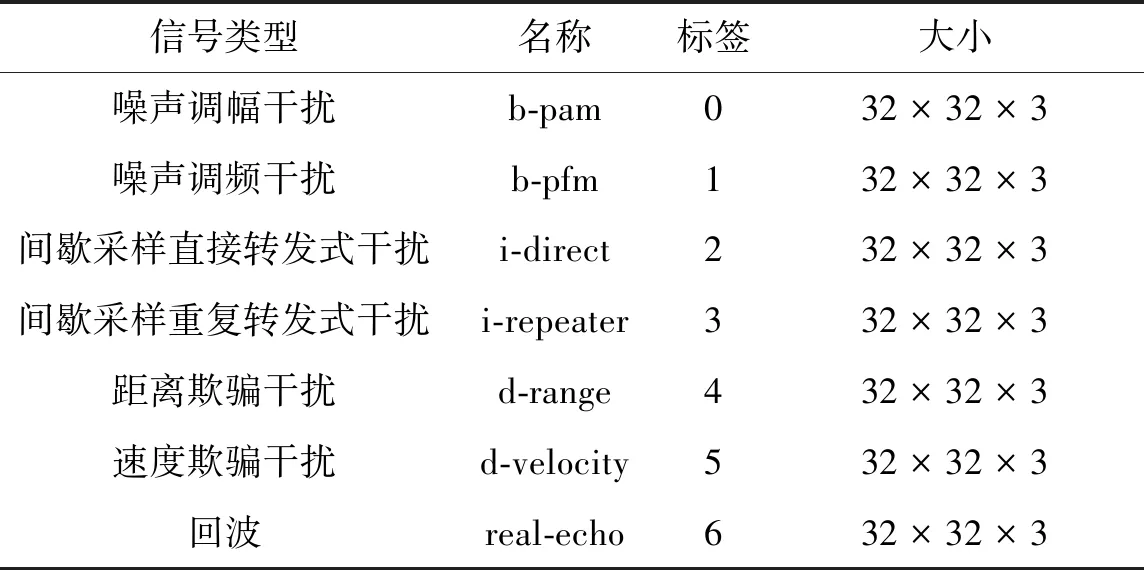
表1 雷达有源干扰信号数据集Tab.1 Radar active jamming signal dataset

2.2 FixMatch算法[13]

作为SSL的重要组成之一，一致性正则化利用了无标签数据，它依赖于这样一个假设：当输入相同图像的扰动版本时，模型应该输出类似的预测。其中模型通过标准监督分类损失进行训练，并通过损失函数对未标记数据进行训练[13]：

(15)

式(15)中，α和pm都是随机函数，所以式中的两项会有不同的值。

基于上述思想，伪标签利用模型本身为未标签数据获取人工标签。设qb=pm(y|ub)，伪标签使用以下损失函数[13]：

(16)

FixMatch的损失函数包含两个交叉熵损失项：应用于标记数据的有监督损失ls和无监督损失lu。具体来说，ls只是弱增强标记示例上的标准交叉熵损失[13]：

(17)

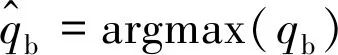
(18)

式(18)中，τ是一个标量超参数，表示保留伪标签的阈值。用FixMatch最小化的损失为ls+λulu，其中λu是一个固定标量超参数，表示未标记损失的相对权重。

2.3 基于FixMatch算法的雷达有源干扰识别方法

在上述理论和仿真分析的基础上，提出基于FixMatch算法的雷达有源干扰识别方法，如图15所示。

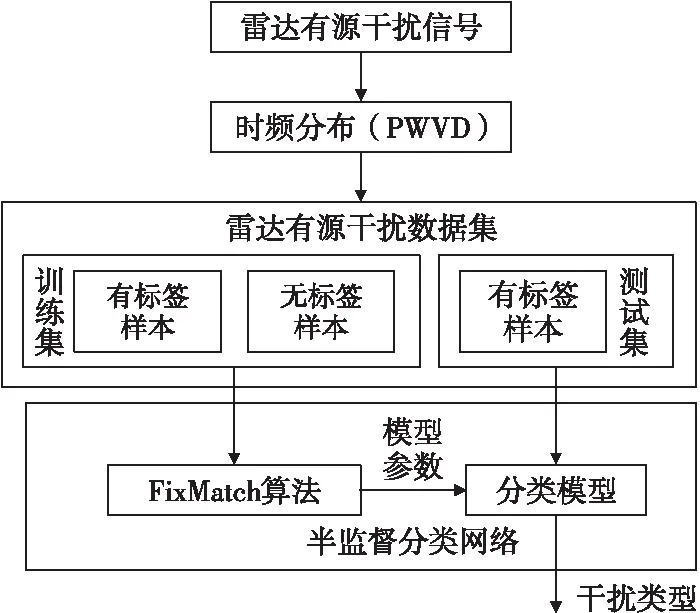
图15 基于FixMatch的雷达有源干扰识别方法Fig.15 Radar active jamming identification method based on FixMatch

具体步骤如下：

1) 生成雷达有源干扰信号样本；

2) 利用时频分析方法提取信号高维特征；

3) 构建雷达有源干扰信号数据集，数据集包含训练集和测试集两个部分，其中，训练集中仅部分样本有标签，而测试集中的样本都具有标签；

4) 使用训练集对半监督分类网络进行训练，保存模型参数；

5) 导入模型参数，利用测试集对分类模型进行测试。

3 仿真结果与分析

仿真实验主要考察样本标签数量对模型性能的影响。实验根据标签数量区分为3种情况：1) 每一类样本有4个标签，共计28个标签，训练次数为128轮；2) 每一类样本有25个标签，共计175个标签，训练次数为25轮；3) 每一类样本有400个标签，共计2 800个标签，训练次数为112轮。其中，训练次数设置按照训练时间大致相当的原则。关于模型的性能优劣，主要通过识别准确率和混淆矩阵对其进行评估[24-25]。

3.1 仿真结果

3.1.1具有28个标签时的模型性能

1) 准确率

经过128轮训练，用时约728 min，模型的识别准确率为87.6%。

2) 混淆矩阵

为了分析具有28个标签时模型对于有源干扰信号的识别性能，绘制模型分类后的混淆矩阵，如图16所示，横轴代表真实标签，纵轴代表预测标签，横轴与纵轴交叉的部分便是混淆矩阵。测试集中每个干扰类型包含1 000个样本，从图中可以看出，回波、噪声调幅干扰、欺骗式干扰、间歇采样转发式干扰等信号识别准确率均大于95.6%，同时，75.1%的噪声调频干扰被误分类为噪声调幅干扰。

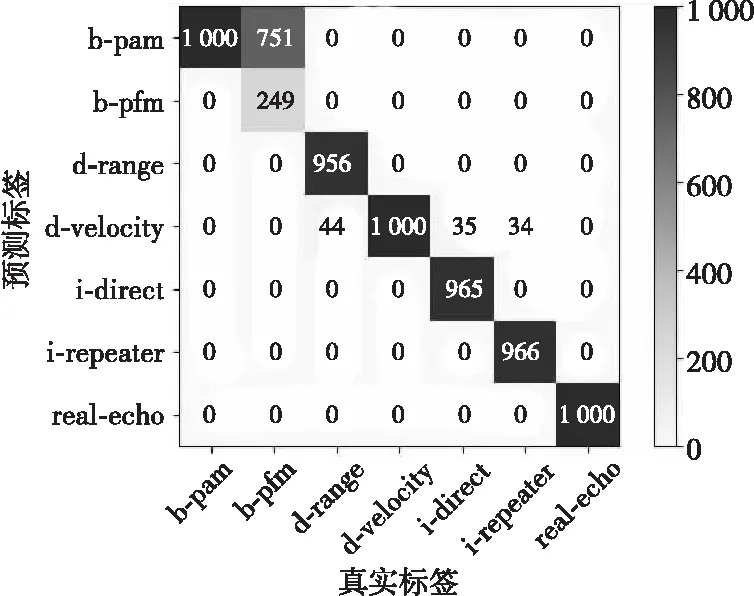
图16 混淆矩阵1Fig.16 Confusion matrix 1

3.1.2具有175个标签时的模型性能

1) 准确率

经过25轮训练，用时约738 min，模型的识别准确率为92.8%。

2) 混淆矩阵

为了分析具有175个标签时的模型对于有源干扰信号的识别性能，绘制模型分类后的混淆矩阵，如图17所示。

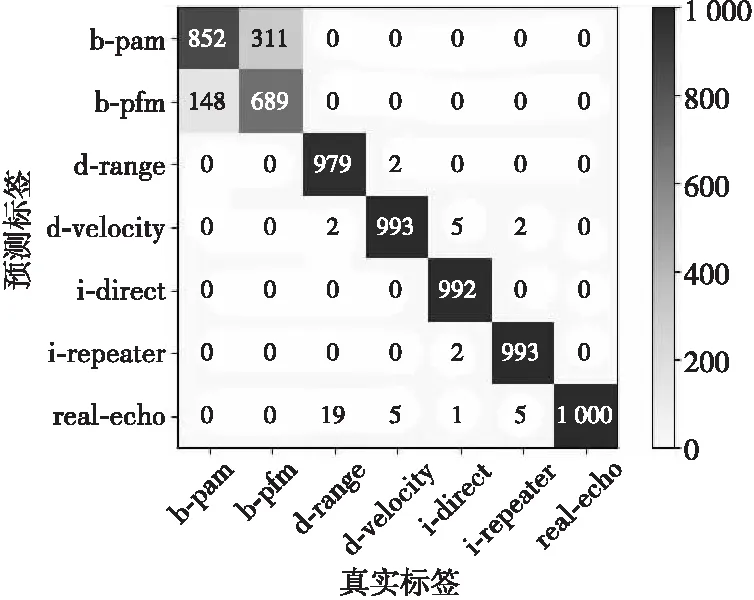
图17 混淆矩阵2Fig.17 Confusion matrix 2

从图17中可以看出，欺骗式干扰、间歇采样转发式干扰和真实回波信号的识别准确率均大于97.9%，而噪声调幅干扰与噪声调频干扰之间存在轻微混淆。

3.1.3具有2 800个标签时的模型性能

1) 准确率

经过112轮训练，用时约733 min，模型的识别准确率为94.7%。

2) 混淆矩阵

为了分析具有2 800个标签时的模型对于有源干扰信号的识别性能，绘制模型分类后的混淆矩阵，如图18所示。

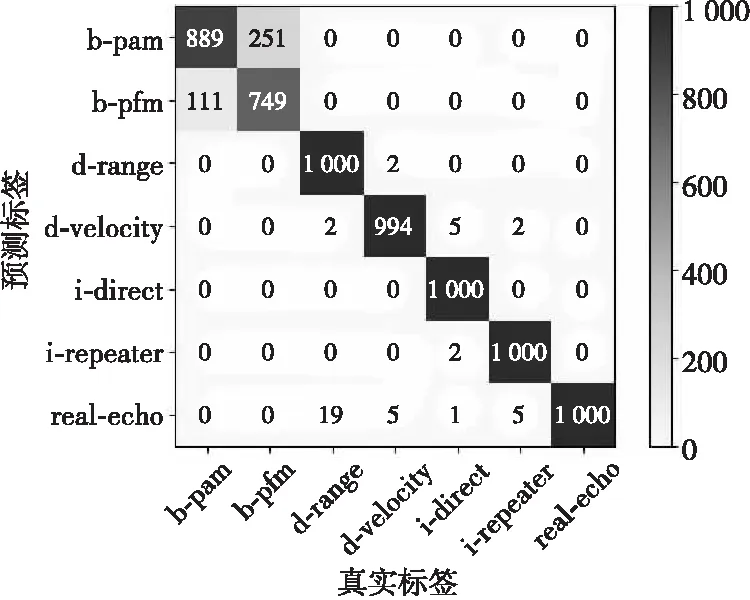
图18 混淆矩阵3Fig.18 Confusion matrix 3

从图18中可以看出，欺骗式干扰、间歇采样转发式干扰和真实回波信号的识别准确率均大于99.4%，而噪声调幅干扰与噪声调频干扰之间混淆程度较3.1.2节得到一定程度的改善。

3.2 结果分析

根据上述仿真结果，分析如下：

1) 由准确率的变化可知，样本标签数量是影响模型性能的重要因素之一。

2) 从图16—图18中可以看出，噪声调幅干扰与噪声调频干扰之间存在混淆，通过标签数量的增加，两者之间的混淆程度得到改善。

4 结论

本文提出一种基于SSL网络的雷达有源干扰识别方法，用于提升具有少量标签的雷达有源干扰信号识别性能。首先，仿真生成有源干扰信号样本，然后利用时频分析方法提取信号高维特征，并运用Python生成雷达有源干扰信号数据集，最后，开展了基于FixMatch算法的雷达有源干扰识别仿真实验。实验结果表明，在数据集具有28个标签时模型精度为87.6%，具有175个标签时模型精度为92.8%，具有2 800个标签时模型精度为94.7%。验证了SSL网络在具有少量标签的雷达有源干扰识别应用中有重大研究价值。下一步工作主要从SSL网络的轻量化方面展开，为其在机载或弹载情况下的应用提供技术支撑。