PSO-SVR 优化模型在基坑变形监测预测中的应用

晏晓红，宋 丽，荣延祥

（1. 深圳市地质局，广东 深圳 518023；2. 长江科学院，湖北 武汉 430014）

近年来随着机器学习的兴起，基于机器学习算法如神经网络、支持向量机等预测模型越来越受到关注和应用，BP神经网络可以通过调整网络自身的权值和阈值来逼近监测数据的非线性映射关系[1-3]。支持向量机在面对非线性、小样本问题时能得到较好的预测结果，在过度拟合、陷入局部最优等问题上相对于其他机器算法有显著优势[4-5]。然而，在预测研究中发现，支持向量机的预测效果对模型参数的选择较为敏感[6]，支持向量机预测精度与惩罚系数C 和核参数σ密切相关。

针对支持向量机模型在预测变形过程中对模型参数选取敏感的问题，本文提出采用粒子群优化算法（PSO）的快速全局寻优功能，优选支持向量机回归模型的参数，利用PSO-SVR 组合模型实现对基坑水平位移监测数据进行预测，并将其与BP 神经网络预测结果与实测值进行对比，验证基于粒子群优化支持向量机回归模型对基坑变形监测预测的有效性。

1 支持向量机回归和粒子群优化算法

1.1 支持向量机回归模型

支持向量机是Vapnik[7]在1995 年首先提出的一种模式识别算法。它通过非线性变换将输入的变量映射到一个更高维的线性空间里，用原空间的核函数取代高维空间中的点积运算，通过有限样本数据的学习训练，获取最优解[8]。支持向量机回归（SVR）是支持向量机（SVM）中的一个重要的应用分支，是一种基于统计学习理论和结构风险最小化原则建立起来的智能算法，对小样本和非线性回归预测等问题具有明显优势[9]。SVR 回归与SVM 分类的区别在于，SVR 的样本点最终只有一类，它所寻求的最优超平面不是SVM那样使两类或多类样本点分的“最开”，而是使所有的样本点离超平面的总偏差最小。

SVR在SVM的基础上，通过引入不敏感函数ε作为损失函数，以容忍高维空间中线性决策函数的边界误差。对于线性回归来说，所寻找的函数为线性函数。

为了达到结构风险的极小化，并考虑可能超过精度的回归误差，引入松弛因子ξ(*)。线性回归可转化为求解如下带约束的优化问题：

式中，惩罚因子C（C>0）为常数，用来控制对超出误差ε样本的惩罚程度。通过引入拉格朗日乘子，将输入空间X中的输入量x经非线性变化映射到另一高维特征空间F中去，将非线性回归问题转化为高维超平面F中的线性回归问题，求其最优线性回归面。回归函数为：

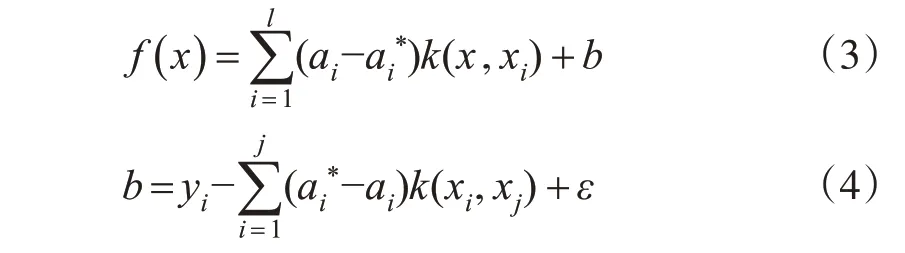
式中，k(x,xi) 为核函数，本文采取径向基核函数RBF，该函数有较强的非线性映射能力，模型选择简单以及回归预测精度高等优点。

式中，σ为径向基函数的核参数。

影响SVR 模型的参数为3 个，即惩罚系数C、径向基函数的核参数σ，以及不敏感损失系数ε。支持向量机的预测效果对模型参数的选择较为敏感，因此，寻找支持向量机回归模型的最优参数极为关键。SVR 预测能力的大小几乎不受参数ε局部变化的影响，训练误差随着ε增大基本保持不变[10]，ε为常用值0.1。故进行迭代寻优的参数为惩罚系数C 和核参数σ，PSO算法的快速全局寻优功能可以优化SVR模型的惩罚因子C和核参数σ。

1.2 粒子群优化算法（PSO）

由Eberhart[11]提出的粒子群优化算法（PSO）是一种进化计算技术，源于对鸟群捕食的行为模拟。将问题的搜索空间类比于鸟类的飞行空间，每个优化问题的解都是搜索空间的一只鸟，即所谓的粒子。粒子群算法属于群智能进化算法，由粒子间相互协作表现出的智能行为控制寻优过程，具有搜索速度快、结构简单、易于实现的特点[12]。PSO 算法具有概念易理解、调整参数少、编程易实现等优点，在神经网络训练和函数优化等领域得到了广泛的应用[13-14]。

PSO 的基本原理是将系统初始化一群随机粒子，每个粒子都是一个可行解，通过迭代搜寻最优值。在每一次迭代中，粒子通过速度更新当前位置，并通过适应度函数计算出其适应值，以判别粒子是否在寻优解范围内。每次迭代都会找出本次迭代中最接近最优解的粒子，其余粒子会跟随该粒子的运动方向逐一搜索，直到所有粒子都在最优解附近。粒子通过跟踪两个极值来更新，第一个就是粒子本身所找到的最优解，这个解称为个体极值；另一个极值是整个种群目前找到的最优解，这个极值是全局极值。粒子群算法是根据以下的公式，更新粒子的当前速度和位置：

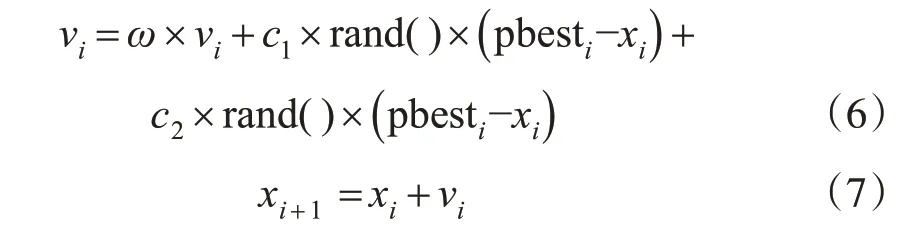
式中，vi为粒子的速度；rand() 为介于（0,1）之间的随机数；xi为粒子的当前位置；c1和c2为学习因子，通常c1=c2=2；vi的最大值为vmax（大于0），如果vi大于vmax，则vi=vmax,ω为惯性因子，其值为非负；pbesti为粒子群的最佳位置。

1.3 评价指标

回归模型预测通常采用标准均方根误差（RMSE）、平均绝对误差（MAE）、平均绝对值百分比误差（MAPE）、平均均方误差（MSE）作为评价指标对预测结果进行评价，取值越小，模型预测的准确度越高。

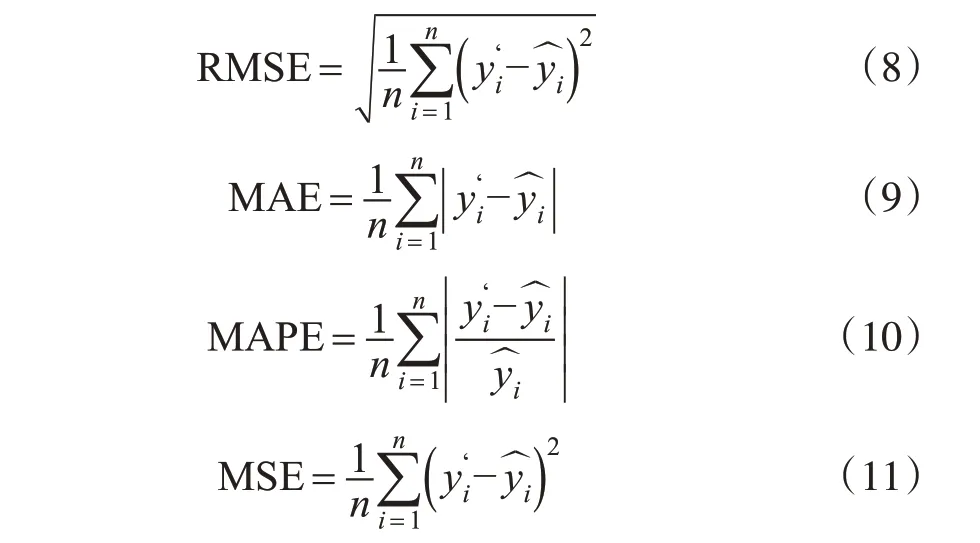
式中，为预测模型输出值；为真实值。

2 实例分析

深圳市国速世纪大厦基坑支护工程第三方监测项目位于深圳市罗湖区桂园街道蔡屋围片区宝安南路与红桂路交汇处西北侧，基坑周边10 m范围内有道路及多栋已建成的高层建筑。国速世纪大厦为商住小区及附属商业裙楼，全通地下室，拟建建筑物设计±0.00标高为9.40 m，设4 层地下室，基坑底绝对标高为-7.00 m，基坑开挖深度为16.40 m。基坑总周长约3 25 m，面积约5 880 m2，基坑支护根据周边环境及地质条件综合考虑安全等级定为一级。

本文采用支护桩顶水平位移测点S4 从2016-09-18～2017-08-28 133 期监测成果以及测点S4 附近支护桩深层水平位移监测CX2#测斜监测孔0.5 m 深度130 期监测成果共两组数据作为实验数据，建立预测模型并进行分析。

2.1 PSO-SVR优化模型预测

为增加训练数据集，引入自回归阶数来丰富数据，自回归阶数定义为5，用前5 期数据预测第6 期数据，依次类推。S4 支护桩顶水平位移监测数据共131期，选取117组训练数据，9组预测。CX2#测斜监测支护桩体深部水平位移数据共130 期，除去自回归5 期，还剩125 期数据，我们选取110 组数据训练，15组预测（表1）。模型训练过程中会随机划分，选取80%数据进行训练，20%数据进行验证。

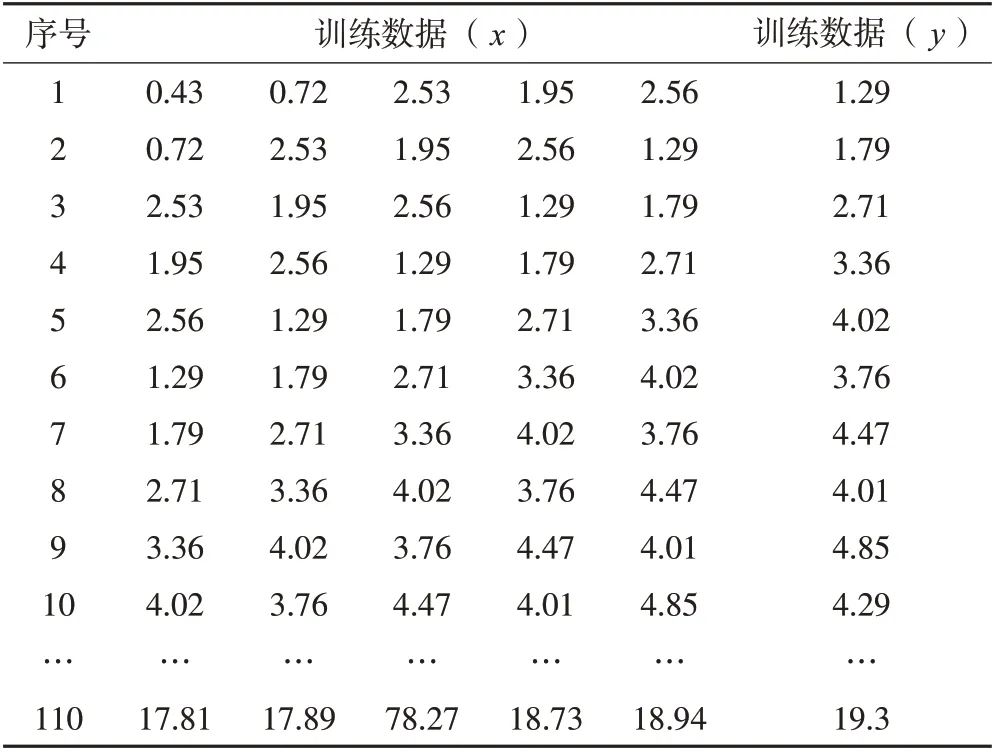
表1 支护桩体深部水平位移数据训练数据集/mm

以支护桩深部水平位移数据为例，设定SVR模型的惩罚因子C 和核参数σ搜索空间为（0，200），PSO 粒子群个数为50，最大迭代次数为100，c1和c2学习因子均为2，惯性因子ω为0.6，最大飞行速度vmax为5，粒子群只为搜索损失最小，RMSE均方根误差可作为粒子群的适应度函数。在MATLAB中得到适应度函数曲线图如图1所示。

由图1 可知，进化迭代20 次后，RMSE 适应度下降不再明显，得到最优的适应度值，此时对应的参数即为PSO-SVR 的最优参数组合，提取对应的C 为98.1346，径向基函数的核参数σ为0.000 2。将C和σ代入SVR模型，即可得到预测结果。训练数据和检验数据的预测值、原始实测数据值对比见图2。

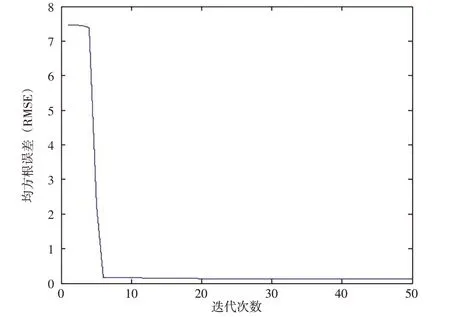
图1 粒子群适应度函数曲线图

图2 PSO-SVR模型预测结果图

2.2 不同模型预测结果对比分析

为了验证本模型实验结果的准确性，以相同的两组数据，采用BP 神经网络模型对实验数据进行预测。定义3层网络，第一层20个节点，第二层40个节点，第三层输出定义1 个节点，每一层都选择Tansig函数，采用梯度下降，学习率为0.01。PSO-SVR模型和BP 神经网络模型预测值与实测值误差对比见表2，检验数据集中2 种模型预测值与实测值的对比图以及预测值残差对比图如图3、4。

通过这2种预测模型的计算结果和数据对比可知：

1）图3 直观地反映出了PSO-SVR、BP 神经网络模型的预测结果与深部水平位移、桩顶水平位移实测值的对比，可以看出PSO-SVR 模型和BP 神经网络预测的变化趋势均与实测值变化趋势基本相同，通过图形对比分析，PSO-SVR 模型预测值与实测值的最接近，更能反映变形监测的位移变化趋势。

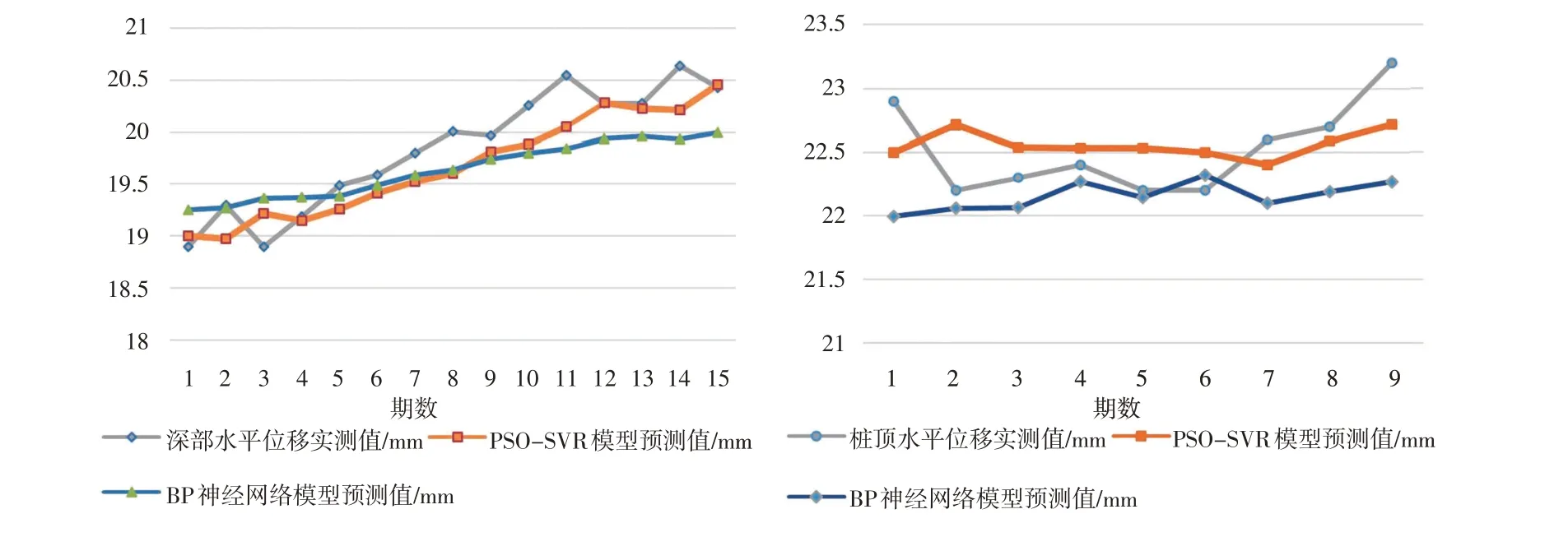
图3 PSO-SVR、BP神经网络模型预测值与实测值对比图

2）表2和图4显示了PSO-SVR、BP神经网络模型的预测值和相对误差，分别计算两组实验数据不同预测模型的标准均方根误差（RMSE）、平均绝对误差（MAE）、平均绝对值百分比误差（MAPE）和平均均方误差（MSE）4个评价指标值，结果见表3和表4。

表3 深部水平位移数据不同模型预测结果的评价指标值

表4 桩顶水平位移数据不同模型预测结果的评价指标值

图4 PSO-SVR、BP神经网络模型预测值残差对比图

表2 不同预测模型检验数据集预测值与实测值误差一览表/mm

从预测结果的评价指标RMSE、MAE、MAPE 和MSE来看，两组数据PSO-SVR模型预测结果的四项评价指标均比BP神经网络预测更小，反映出其预测结果准确度更高，PSO-SVR模型对本次变形监测数据具有理想的预测结果，能满足变形监测数据预测的需要。

此外，PSO-SVR 模型在全局寻优方面更出色，多次运行后RMSE 更小，运行效率也较BP 神经网络更高。

3 结 语

本文采用PSO-SVR 优化组合模型进行基坑桩顶水平位移和深部水平位移监测数据的分析与预测，通过粒子群（PSO）优化算法选取SVR 中核函数的参数惩罚因子C和核参数σ这两个关键参数。实验结果表明，PSO-SVR优化组合模型对样本训练后得到的预测值与实测值的均方根误差最小，同BP 神经网络相比，对基坑变形监测预测的准确度更高，预测值与实测值最贴近，更能反映变形监测的位移变化趋势，是基坑变形监测预测的有效方法。此外，本文仅选取径向基核函数RBF作为SVR模型的核函数，可进一步研究如何确定有效的核函数使SVR模型的精度更高，以及对SVR参数优化算法，都需要进一步深入研究。