基于云分形的自然景物模拟研究

张盼盼，秦 昆，郭培煌

（1. 北京华为数字技术有限公司，北京100095；2. 武汉大学遥感信息工程学院，湖北 武汉430072；3. 北京地平线信息技术有限公司，北京100094）

云模型实际上是一种概率模型，通过生成符合一定分布的云滴，对事物的随机性进行描述。简而言之，每一个云滴都是定性概念的一次随机估值及该估值对定性概念的隶属度的组合。通过建立事物的云模型，实现了随机性与模糊性的统一描述。将这种模型和分形相结合，形成云分形思想，可以将复杂事物自相似性中的随机性，通过云模型来表征，体现出不确定性的多样性，而扩展云中的期望值则反映出不确定性现象中所蕴含的规律性。

1 分形算法

分形模拟的方法主要有递归算法、LS 法、IFS法、分形插值方法、DLA 模型法、BSP 模型、L-系统等[1]。

之前在对植物进化和形态的相关研究中提出过L-系统的分形算法，它在植物拓扑层面的模拟上相对有效。该算法在树木拓扑结构模拟上具有简明、高结构化和易实现等特性，因此成为了主流的树木个体拓扑模拟方法[2]。

L-系统是一类独特的迭代过程，其核心概念是重写，即用一个重写规则迭代地置换初始对象的各个部分来确定一个复杂的对象。

以树的例子来说明，常用的符号包含：“ L ” ,“+”,“-”,“ [”,“ ]”这5 种符号，分别表示的意义如下：

1）L：在当前所处位置朝向上前进一步，并画线；

2）+：逆时针旋转一定角度；

3）-：顺时针旋转一定角度；

4）[：将当前信息压栈，即进入到某一个分支；

5）]：将“[”时刻的信息出栈，即退回到主线上。

L-系统算法在实现上分成两个过程，分别是：

1）根据规则生成用于模拟树木的完整字符串。①定义并设置公理（即初始字符）和产生规则（即字符替换规则）；②定义并设置生成树木的起始点、初始角度、迭代步长和迭代上限等控制参数；③根据产生规则用替换字符串替换当前完整的字符串，不断循环迭代，直至得到最大的迭代次数为止。

2）在生成完整字符串之后，开始读取逐个字符并依据规则画图。①读取完整字符串中的每个字符；②根据读取到的字符（“L”,“+”,“-”,“[”,“ ]”）采取相应动作。

上述方法在绘制分形树时，符号“L”代表树干和旁枝，符号“+”和“-”代表树枝的生长方向，符号“[”代表绘制时需要分枝，将当前已经绘制的树枝状态缓存下来，开始绘制分支方向，并将符号后面的字符在分支方向开始绘制，直到遇见符号“]”，符号“]”代表退出当前分支方向的绘制，回到符号“[”开始的主方向上，如图1所示。

图1 LS分形树

L-系统反映的是植物结构当中“单平面”的形态，是一个二维图形，不能体现植物形态的丰富层次，更无法在具体实现中对植物中每一个器官及每一个层面的特征进行细节约束和绘制。BSP 是一种新型的空间剖分技术，于1980年首次由Fuchs提出并在平面对空间的剖分中得到应用，建立起空间二叉树结构，如图2 所示。BSP 空间剖分技术是以递归方法为基础，将平面空间分割成两个半空间，依次进行不断的细分，直到不可再分割为止。这样就可以对每一个空间中的对象进行更加细致的描述，从而更多关注对象的结构和行为。因此在大自然树木模拟过程中，需要充分发挥空间剖分技术所带来的优势，使得植物形态结构特征的模拟更加出色和逼真。

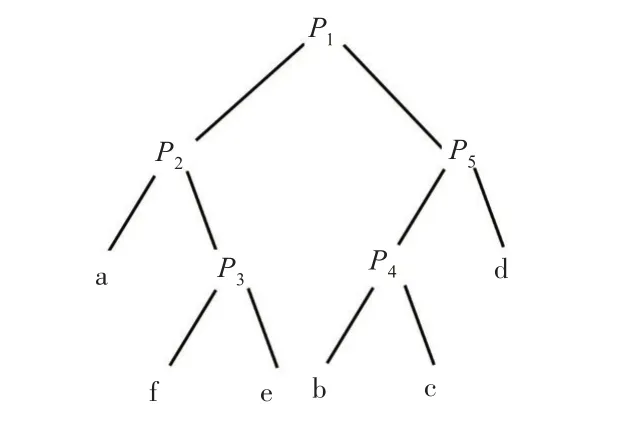
图2 BSP形成的空间二叉树

在具体植物模拟过程中，为了更好地对植物的枝干和树叶进行更为细节的描述，在L-系统的基础上引入BSP方法，递归方式剖分空间平面，可以控制植物主干上左子树、右子树的绘制顺序，控制分枝的长短和分枝在结点上的旋转角度，同时也能控制树叶的偏转方向。结合各个细节方面的控制，以此来逼近植物的真实形态，并争取能够模拟植物在特殊情况下的形态，使得模拟出来的植物形态更加生动、逼真。

下面以树木模拟过程来描述BSP方法的运用。通常情况，递归深度、偏转角和步长是影响树木生长形态的主要参数。具体数目绘制过程如下：

1）递归深度（iter）：反映树木的整体形态，比如树木的高低、粗细等外观特征，这是最主要的参数，树木的枝干会随着递归深度的递减而逐渐变细。

2）偏转角（angle）：反映分枝的树木茂盛和集中程度，偏转角过大或过小则剪枝。在实际的植物模拟过程中，偏转角不能一成不变，它需要有一定的随机幅度。当递归深度较大时，意味着当前处于较为底层的绘制状态，即分支和树叶的绘制层级，可适当减小分枝偏转角的随机幅度，使树木看起来长势更为集中。同时考虑到树木生长过程中的顶端优势，当分枝和最初主干之间的夹角较小时，需要在分枝上绘制两个子树，使分枝看起来更长。

3）步长（step）：反映叶子的长度。根据实际情况，需要控制叶子的长度。

4）根结点的坐标：反映植物生长的具体位置。

迭代函数系统（iterated function system，IFS），1981 年由Hutchcison 首次提出用压缩映射方法来产生分形，1985 年由美国佐治亚理工学院数学教授Barns⁃ley M 发明了迭代函数系统，后来Stephen[4]等人进行了公式化，引入到图像合成领域中，其理论方法是分形自然景物和分形图像压缩理论的基础。

IFS 的优势性在许多物体的建模问题中得到体现，尤其是对自然物的计算机模拟的优势更为明显。例如：IFS 可以用来产生各种形态的植物、丛林、山川、云烟等[3]。用IFS可以很容易地对这些自然景物进行描述，关键是仿射变换参数的选取。

在上述思想的牵引下，IFS 被证明集合对象的全貌和其局部特征在仿射变换下具有自相似性[5]，如果通过定义全局对象集合以及若干个仿射变换参数，可以实现将整体形态变换到其局部形态上，并且通过反复迭代，可以产生满意图形。

通过相似变换可以实现物体对象的自相似，通过仿射变换也可以实现自仿射。实际上，物体对象的自仿射性也是自相似特性的一种扩展方式。相似变换被看作是从局部到整体的等比例变换，而仿射变换则是局部到整体的不等比例变换[4]。

IFS 生成的迭代算法有两种：一种是确定性迭代算法，另一种是随机迭代算法。通常IFS 生成采用的是后者。

根据仿射变换的数学表达式：

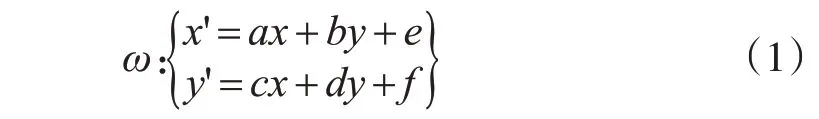
式中，ω为仿射变换；x和y为变换前的图形坐标值；x′ 和y′ 为变换后的图形坐标值；a，b，c，d，e，f为仿射变换系数。

对于一个复杂的图形，需要多个不同的仿射变换来实现。在随机迭代算法中由带有概率的IFS 仿射变换集{W1，W1，W1，…，WN}和一个概率集{P1，P2，P3，…，PN}组成，可表示为：

式中，a、b、c、d，e、f、P这7 个参数被称为IFS码，仿射变换集控制着图形的结构和形状，每个仿射变换对应一个调用概率P。通常情况下，IFS 码的组数决定了分形图形的复杂程度；各组IFS 码的取值决定了图形的细节问题。

IFS算法步骤如下：

1）系统生成随机数R，使R落在0～1之间。

2）给仿射变换组分配概率空间，判断随机数落入的概率空间范围。

3）系统调用相应空间的IFS码，获取仿射变换参数。

4）由仿射变换计算新的x，y。

5）在（x，y）处画一个点。

6）将上一次的x，y作为下一次的初始x，y重复步骤（1～5），直到满足条件为止。

2 云模型优化分形算法

云模型是用自然语言值表示的某个定性概念与其定量表示之间的不确定性转换模型，采用云的3 个数字特征（Ex，En，He）表示定性概念，体现了模糊性、随机性以及二者之间的关联性。自然科学和社会科学中大量的随机现象基本上都是服从正态分布的，在后续的研究过程中，李德毅院士等人构造了正态云模型，证明了正态云模型具有的普适性。目前，云模型已经成为处理定性概念与定量描述的不确定转换模型，从提出开始，已成功地应用到自然语言处理、数据挖掘、决策分析、智能控制和图像处理等诸多领域。

云模型是通过期望Ex、熵En、超熵He3 个数字特征来表现的，如图3 所示。这3 个数字特征反映定性概念的整体特征，表示概念的不确定性。通过特定的云发生器算法来实现定性概念和定量表示的不确定转换，同时揭示了模糊性和随机性之间的关联性。

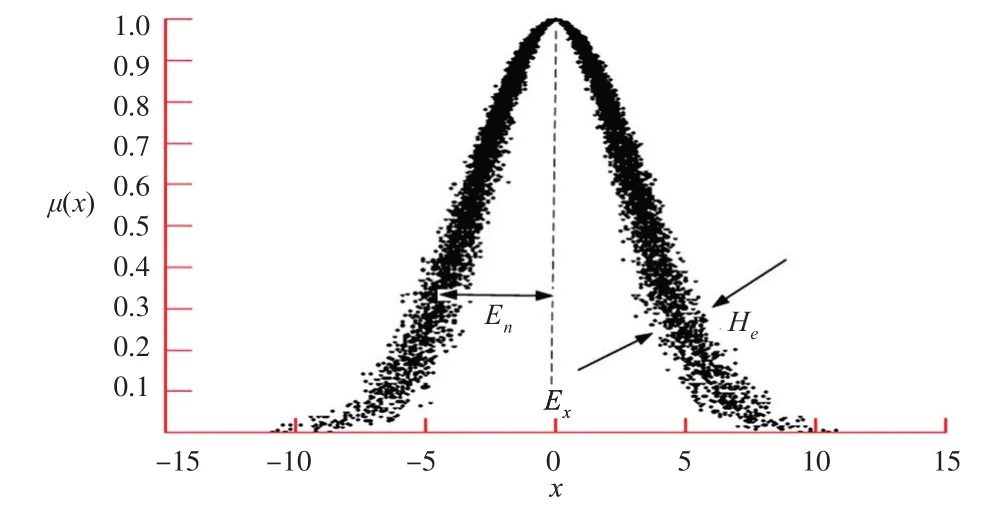
图3 云模型的数字特征示意图

期望Ex：云滴在论域空间分布的期望，是最能够代表定性概念的点，是这个概念量化的最典型样本，反映了这个概念的云滴群的云重心。

熵En：定性概念的可度量力粒度，熵越大，通常概念越宏观，也是定性概念不确定性的度量，由概念的随机性和模糊性共同决定。这种不确定性主要表现在以下三点[6]：

1）熵是定性概念随机性的度量，反映了能够代表这个定性概念的云滴的离散程度。

2）熵又是定性概念亦此亦彼性的度量，反映了论域空间中可被概念接受的云滴的取值范围。用同一个数字特征来反映随机性和模糊性，也必然反映它们之间的关联性。

超熵He：熵的不确定性的度量，即熵的熵，由熵的随机性和模糊性共同决定。反映了每个数值隶属于这个语言值程度的凝聚性。超熵的大小间接地表示了云的离散程度和厚度[7]。超熵越大，云滴的离散度越大，隶属度的随机性越大，云的厚度也越大。

云模型不再强调精确的函数表示，而是利用3个数字特征来表示反映概念的整体特征，仅用3 个参数就能勾画出由成千上万的云滴构成的整个云来，把定性概念中包含的模糊性和随机性完全集成到一起。

正态分布广泛存在于自然现象、社会现象、科学技术以及生产活动中，在实际中遇到许多随机现象都服从或者近似服从正态分布，而中心极限定理也从理论上阐述了正态分布的普适性[8]。

正态云模型是最基本的云模型，是表征语言原子的有力工具之一。考虑到许多随机现象并不能用正态分布来描述，李德毅等将正态分布扩展为泛正态分布，为正态云提供了一个弱化形成正态分布条件的独立参数（超熵），来衡量偏离正态分布的程度。

通过给定云的3 个数字特征，可以运用计算机来计算生成一系列的云滴，这些云滴共同组成的一个云模型的3个数字特征就是事先给定的值。

设U是一个用精确数值表示的定量论域，C是U上的定性概念，若定量值x∊U，且x是定性概念C的一次随机实现，若x满足x～N(Ex,En′2) ，其中，En′～N(Ex,He2)，且x对C的确定度满足

则x在论域U上的分布称为正态云。正向正态云发生器如图4所示。

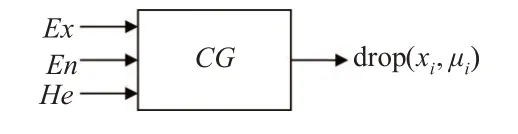
图4 正向正态云发生器

正向正态云发生器输入的是云的3 个数字特征（Ex，En，He）和需要生成的云滴的个数（n）[12]；输出的是要求的n个云滴x及其确定度u。

云分形的思想是通过云发生器，结合函数迭代，将分形算法与云模型理论结合起来，形成云分形的算法。云模型与分形相结合，可以更好地模拟出千姿百态的自然景物，同时发挥两者的长处。更重要的是，可以把自然景物自相似性中包含的随机性，通过云模型进一步显示出来，可以体现不确定的多样性，同时又能用云模型的期望值来反映不确定现象中蕴含的规律性。

3 实验方法及结果分析

3.1 BSP+L系统+云模型的云分形方法在植物模拟中的研究

本文以树木为模拟对象来研究BSP 和L 系统方法结合的运用。一般情况下，影响树木生长形态的主要参数，及其画树过程中的细节如下：

1）递归深度（iter）：递归深度决定树木的高矮、粗细等整体形态。树木的枝干会随着iter 的递减而逐渐变细。本实验在递归过程画分枝时，采用云模型随机的选择植物枝干上左子树、右子树的绘制顺序，当iter小于1时，画叶子。

2）偏转角（angle）：为了让植物模拟更逼真，分枝的偏转角需要有一定的随机幅度，用于决定树木茂盛和集中程度。本实验采用云模型来控制偏转角，输入不同的期望值Ex 来控制偏转角以达到不同的效果。

3）步长（step）：控制叶子的长度。根据实际情况，要控制叶子的长度。

4）根结点的坐标：给出植物绘制的初始位置。

如图5所示的树木模拟，首先采用BSP+L系统这种方式来模拟树木生成效果，同时引入云模型的云分形方法在初始化参数下模拟树木生成，图中是一次随机实现对照图。其中，层数（递归深度）为6，步长为250，随机决定分枝方向的云模型参数为（0.5，0.166 667，0.01），侧枝偏转角的云模型为（0，5，0.1）。

图5 云分形优化前后效果图

需要说明的是，递归深度反映的是树木的高矮粗细，步长反映的是叶子长度，本文考虑到执行效率和美观程度，设定层数为6，步长为250，而决定分支方向设为0.5 是考虑到生成左侧和右侧分支的公平性，在0～1 之间选择折中数值，侧枝偏转角的设定不宜过大，在10°范围内波动，更好的展现出树木的真实性，以上参数设定为其他数值不影响本文的结论。保持这些参数不变，进行更多次实现，可以产生更多形态各异的分形树，如图6所示。

图6 相同参数下云分形方法模拟的树木效果

上述实验发现，云模型的引入，在控制树木的高矮粗细和茂密程度方案不仅表现出巨大的优势，同时在树木模拟多样性方面，也相当出众，能很好的体现出大自然的多样化。

3.2 改进的IFS云分形方法在植物模拟中的研究

传统IFS 方法的要点是如何根据概率集来确定每一次迭代时所选取的仿射变换，即如何使仿射变换参数的被选中率与概率集相同。选择云模型来产生随机数，其作用不仅仅是像rand函数那样产生随机数便作罢，另外一个更重要的作用是在一幅待产生的图像中，针对其中不同的拼贴对象，可通过调整云模型的期望值，使得产生的随机数更大概率地落入我们期望的范围，这样便能够有针对性的来选择某一组或几组仿射变换，这样选择的效果便使该拼贴对象部分产生的图像包含点数更多，图像内容更丰富饱满。

本次实验采用正态云发生器产生随机数，对比分析传统的rand 随机数方法。实验选定的IFS 码如表1所示。

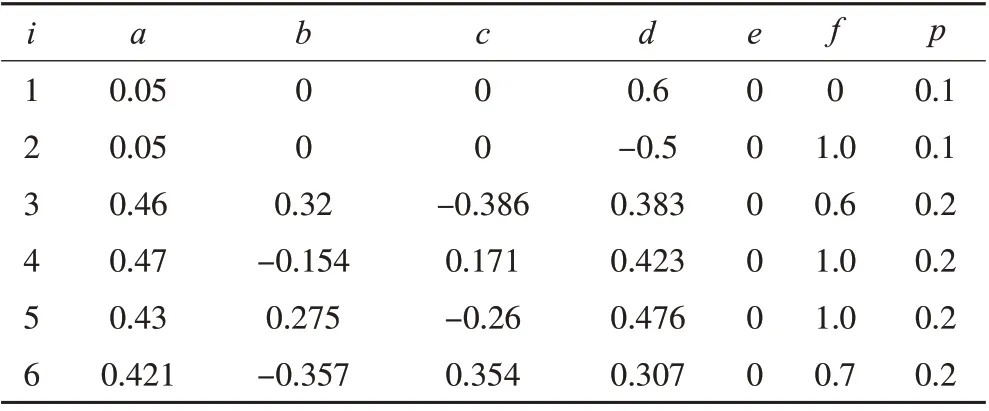
表1 生成IFS树的IFS码

用正态云发生器产生的云滴作为随机数，为了更进一步突出树梢末端的茂密程度，需要将产生的IFS码控制在表1 所示的i=2～5，即概率分布在0.2～0.8之间，因此本文设定云滴期望为0.5，墒为0.3，参数也可以存在一些微小的调整，如图7为引入云模型优化IFS算法的前后对照图。

图7 IFS树及云IFS树

上述实验发现，采用正态云发生器来取代传统的随机函数Rand，可以更好地控制树木生成的局部特征，使得系统可以按照期望的方式来绘制树木。更为直观的是，云IFS 树的生成让植模拟更加生动饱满。

3.3 实验结果分析

在模拟树木时，传统的传统递归算法和确定性L-系统算法中，其树枝长度和旋转角度在每次迭代时都不会发生变化。本文在编程设计绘图函数时用由云模型中的正态云发生器产生的云滴作为随机因子，使树枝长和旋转角度都乘以一个范围可控的随机数，这样使得在迭代过程中的树枝长度略有差异，且画线时旋转的角度有一定的随机幅度，模拟出来的树木不会僵硬死板。同时，可根据不同情况适当修改云模型的参数（期望、熵、超熵），以此来模拟同一类植物的不同形态，使模拟的植物形态更加自然逼真。

针对传统的IFS（迭代函数系统），对由自然景物图形提取分形几何对象信息的原理进行了深入的探讨和研究。一方面采用交互式传统方法提取和输入IFS码，另一方面，在待产生的图像中，针对其中不同的拼贴对象，通过调整云模型的期望值，使云发生器随机数更大概率地落入我们期望的范围，使我们能够有针对性的选择某一组或几组仿射变换，这样选择的效果便使该拼贴对象部分产生的图像包含点数更多，图像内容更加丰富饱满。

4 总结与讨论

分形理论被广泛应用于模拟自然景物的表达，存在各种各样的算法，但由于自然界的物体又不是严格自相似的，它们的自相似性只在统计上成立，且自相似的“层次”结构是有限的。本文主要利用云模型理论来优化传统的分形算法，研究云分形在自然景物模拟表达上的逼真度和可行性。

虽然云模型的引入，在自然景物的模拟方面开展了一定的工作，但仍然需要持续对云分形方法进行探讨和应用，在本文的基础上，今后可以从以下两个大方面重点展开研究：

1）在自然景物模拟方面：①在三维环境中进行多种自然景物的模拟，使模拟的自然景物更具有立体的真实感；②对自然景物的细节进行描绘，如树干的纹理，植物的果实、花朵等；③对植物在不同环境条件的生长进行定性定量的研究，确定其生长比例系数，实现接近真实植物生长的动态模拟控制。如：不同土壤环境生长下的树、不同气候环境下生长的树等。

2）在云分形的不确定性分析方面：目前云分形方法已经在分形模拟、拓扑网络模拟等方面有了成功的应用。扩展云的期望在不同的应用背景下，具有不同的意义，反映了不确定现象中蕴含的规律性。如何将云分形方法用于更多的领域，如种群变异、地貌变迁等，还需要进一步研究。