基于四元组度量损失的多模态变分自编码模型
陈亚瑞,杨剑宁,吴世伟,刘 垚,王晓捷
(天津科技大学人工智能学院,天津 300457)
多模态数据处理广泛存在于自然科学、工程技术等领域,不同模态的数据往往是对同一事物不同形式的表示,又各自具有独特的性质[1-3].在医疗健康研究领域,智能手术室中的多模态数据包括场景 RGB图像、深度图像、红外图像、音频等,不同模态数据包含的信息既相互冗余又相互补充[1].在机器人等智能设备工程技术领域中,设备的深度摄像头会同时采集深度图像与 RGB图像,当受光线等外部因素影响某模态图像成像质量时,可利用另外的模态图像进行辅助去噪[1-4].
采用概率生成模型处理多模态数据是一个重要的研究领域,早期基于能量的玻尔兹曼机与自编码器模型在处理多模态数据中已经取得了较好的效果.随着传感器技术的发展,人类对数据的获取无论从粒度上还是量级上都有了很大的飞跃,获取的数据本身往往具有高维度、海量性等特点,给多模态数据研究带来了更大的难度与挑战.早期的模型不能有效地处理大规模数据场景下的模型训练与推理问题,而变分自编码(variational auto-encoder,VAE)[5-6]的提出很好地解决了该问题.研究基于 VAE框架通过建模数据的条件生成过程,实现模态之间的数据交叉与转换生成,但这些工作未从生成角度进行多模态数据建模,限制了模型的表示能力[7-11].对多模态联合数据分布的建模包括联合多模态变分自编码器(joint multimodal variational auto-encoder,JMVAE)模型[12]、多模态变分自编码器(multimodal variational autoencoder,MVAE)模型[13]和专家混合多模态变分自编码器(mixture-of-experts multimodal variational autoencoder,MMVAE)模型[14]等.这些模型通过建模多模态数据联合概率分布实现多模态数据的表示、条件生成,比分别建模不同方向上条件概率分布的训练开销更低,数据表示更有效.但是,这些模型没有对数据进行解耦表示.文献[15]提出了解耦的多模态变分自编码器(disentangling multimodal variational autoencoder,DMVAE)模型,该模型通过将模态共享信息与私有信息分开表示,并最小化隐向量的互信息进行解耦表示,通过噪声对抗估计损失在隐空间对齐共享隐向量,效果较好,但该模型仍然存在数据生成质量不清晰与共享私有信息抽取不准确的问题.
已有的研究工作对不同模态数据之间的共享信息没有显式的约束,这使多模态数据的共享信息与私有信息不能被高效地解耦表示,进而导致信息抽取不准确、生成数据模糊.本文提出基于四元组度量损失的多模态变分自编码(quadruplet metric loss based multimodal variational auto-encoder,Q-MVAE)模型,在分开建模共享信息与私有信息的基础上,建模不同模态的联合概率分布与单模态边缘概率分布,并且引入了四元组度量损失约束共享隐向量在隐空间对齐,使模型获取更好的数据生成与表示能力.模型可以分别有效推理多模态数据的共享表示和私有表示,这些表示不仅能够进行准确的、高质量的多模态数据交叉生成与转换生成,而且能够用于多模态数据分类等下游任务.相关的定性与定量实验证实了本文模型拥有更好的数据表示能力与生成能力,同时表明模型对私有信息生成因子展现了一定程度的解耦表示能力.
1 相关工作
1.1 多模态概率生成模型
早期基于能量的玻尔兹曼机与自动编码器模型的生成模型[8-10]在视频、音频等多模态数据下的语音识别任务中取得了较好的识别准确率.这些模型往往采用马尔可夫链蒙特卡罗方法训练模型,难以处理高维大数据的场景.研究人员[5-6]提出了 VAE框架,通过引入变分推理与重参数化技巧,使生成模型可以在大数据场景下进行有效训练.这使以 VAE为框架的多模态概率生成模型成了多模态数据处理领域的重要研究方向.Kingma等[7]和 Sohn等[8]在 VAE框架的基础上提出了条件变分自编码器(conditional variational auto-encoder,CVAE),通过最大化条件似然,可以基于标签等信息进行有条件的数据生成.基于 CVAE的改进模型[9-10]可以学习模态间的条件关系,但是条件关系是单方向的,模型的推理表示能力有限.Wang等[11]提出了双向变分典型相关性分析模型 (bidirectional variational canonical,correlation analysis,BiVCCA),基于典型相关性分析思想,设计学习两模态数据私有信息的编码器,实现了数据交叉生成,但是其条件关系也是单向的,模型训练开销较大,难以扩展到两模态以上场景.
Suzuki等[12]提出了JMVAE模型,该模型直接建模多模态数据的联合分布,这使其比建模条件分布的模型具有更低的训练开销,也可以有效地从联合分布中推导条件分布,然而该模型也存在计算开销会随着模态数目的扩展呈指数级增长的问题.Wu等[13]提出了MVAE模型,Shi等[14]提出了MMVAE模型,这些模型都直接建模多模态数据的联合分布,并利用边缘后验分布拟合联合后验分布.其中,MVAE模型通过引入专家积函数[16](product of experts,PoE)对边缘后验分布进行几何平均运算,MMVAE通过引入专家和函数(mixture of experts,MoE)对边缘后验分布进行算术平均运算,都较好地解决了多模态下的计算开销问题,也一定程度解决了缺失模态下的推理表示问题.Sutter等[17]提出了专家混合积函数变分自编码(mixture,of products of experts variational autoencoder,MoPoE-VAE)模型,该模型提出了一个更泛化的多模态生成模型的下界,整合了 MVAE与MMVAE模型的特点,并在其理论框架内将这两个模型视为其模型的特殊情况.但是,上述工作都未考虑多模态数据共享信息与私有信息的解耦表示.Daunhawer等[15]提出了DMVAE模型,该模型对每个模态的共享信息与私有信息都进行了解耦表示,并引入噪声对抗估计损失在隐空间对齐共享隐向量,有效地提高了模型的数据表示能力与生成能力,但该模型没有显式地约束共享隐向量,导致该模型存在信息抽取不准确以及生成的数据质量模糊的问题.
1.2 度量学习
利用样本之间的相对距离关系学习数据表示的度量学习与对比学习在模式识别、表示学习领域取得了出色的效果[18-21].Schroff等[18]提出了三元组损失并应用于人脸识别中,其作为一种度量学习方法通过约束样本标签,使相同的人脸图像在编码空间的距离小于不同样本标签来学习人脸的向量表示.Chen等[22]提出了四元组损失并将其应用于行人重识别任务中,四元组损失能够约束模型在特征空间更好地识别不同摄像头视角下的行人.Ishfaq等[23]将三元组损失引入 VAE模型,利用不同标签的三元组正负样本进行对比训练,数据表示效果较好,同时在隐空间编码了更多的相似语义结构信息.Shi等[24]提出利用样本之间的相关性关系进行对比学习,有效提升了MVAE、MMVAE等多模态生成模型的训练效率.
本文受到上述工作的启发,在将共享信息、私有信息分开推理表示的基础上,将四元组度量损失引入概率生成模型中,以显式约束模型编码网络学习到不同模态的共享信息,在模型训练时同时考虑数据完整与模态数据缺失的情况,以使模型具备在模态数据缺失情况下的推理表示能力与生成能力.
2 背景知识
本文模型基于 VAE[5-6]概率生成模型框架,该框架使模型可以在高维大规模数据场景下,使用随机梯度下降方法进行有效训练.
VAE框架假设给定观测数据x,以及对应的隐变量 z,其 生 成 过 程 为 x ~ pθ(x|z ),其 中 z ~ p(z)=N ( 0,I),θ是生成器网络p的参数.VAE的目标是最大化式(1).
但是,式(1)是不可计算的,VAE转而计算其证据下界(evidence lower bound,ELBO),即
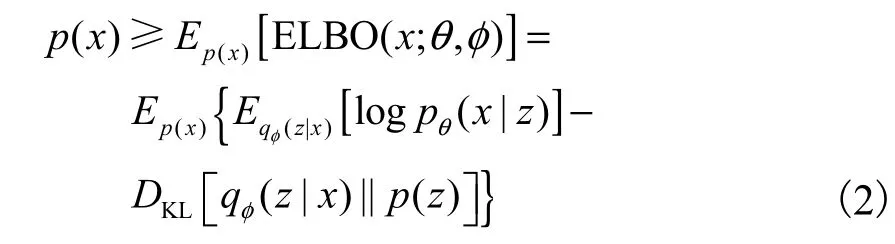
式 中 : Eqφ(z|x)[l o g pθ(x|z)]为 负 重 构 误 差 ,DKL[[qφ(z|x) ||p(z) ]]为正则化项;pθ(x|z)为生成器网络,参数为 θ;qφ(z|x)为编码器网络,参数为φ.VAE的目标是利用参数 θ和φ最大化式(2).为了使其能够在神经网络上进行训练,提出了对隐变量z进行重参数化,即假设qφ(z|x)为高斯分布 N (z;μ, d iag(σ2) ),φ={μ,σ2} ,将 z ~ qφ(z|x)重参数化为z =μ+σ⊙ε,其中ε~ N(0,I).以 VAE为框架的模型训练完成后,就可以得到 1个编码网络和 1个生成网络.编码网络对数据进行表示推理,生成网络随机生成、重构数据[5, 25-26].
3 本文模型
3.1 模型架构
针对多模态数据的表示与生成问题,本文提出Q-MVAE模型,模型假设多模态数据生成过程由共享隐向量与私有隐向量共同决定,该假设已经在最新的一些研究工作中展现了其优越性[15].Q-MVAE模型通过共享隐向量与私有隐向量的组合生成特定模态数据,在推理过程中,模型也分别推理每个模态数据的共享隐向量与私有隐向量.对于多模态数据共享信息抽取与训练,本文提出了四元组度量损失,用于在隐空间对齐共享隐向量,显式地约束编码网络学习不同模态数据的共享信息,模型架构如图1所示.
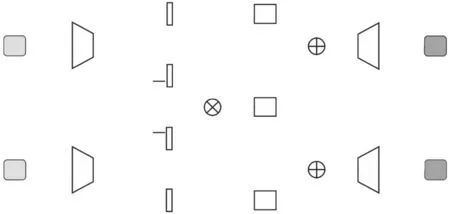
图1 Q-MVAE模型架构图Fig.1 Architecture of Q-MVAE model
3.2 模型生成与推理过程
Q-MVAE模型可以处理两模态及以上模态数量的多模态数据,本文以两模态数据(x,y)为例进行推导,假设不同模态数据样本包含相同的共享信息与不同的私有信息,令生成数据(x,y)的共享隐向量为 z,私有隐向量分别为hx与hy.模型对数据的联合概率分布建模为

其中:p ( z) 、 p ( hx)、 p (hy)分别为隐向量 z、hx与hy的先验分布,均服从各向同性的高斯分布;pθx( x |z,hx)和 pθy( y|z,hy)分别为 x和 y的生成器,参数为θ={θx,θy}.对于两模态数据集,模型的目标是最大化数据联合概率分布与边缘概率分布的对数似然函数,以得到模型参数.
为了符号表示简便,下文以单观测样本的多模态数据对(x,y)为例进行推导,单观测数据对的边缘概率分布为
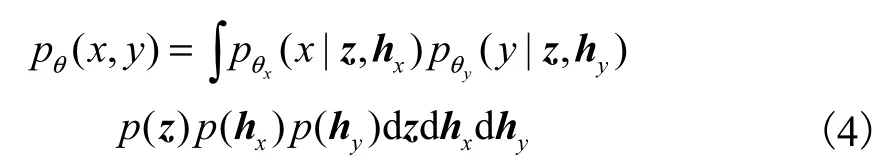
但是,式(4)中的积分是难解的,本文采用变分推理的方法进行近似求解,引入变分分布 q ( z,hx,hy|x,y)作为真实后验分布的近似,对似然函数进行变换

对变分分布进行分解
其中:qφhx(hx|x)与 qφhy(hy|y)为Q-MVAE模型的私有信息编码器,参数分别为
将式(3)与式(6)代入式(5)中,可得到lnpθ(x,y)的变分下界
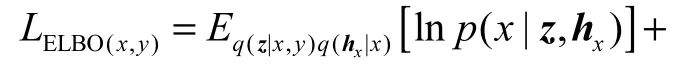
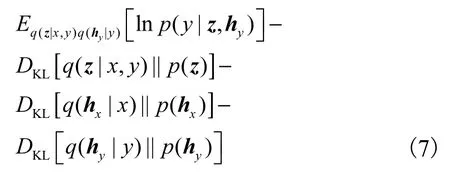
其中:q(z|x,y)是x和y的共享隐向量近似后验概率分布.当x和y同时存在时,模型在训练时采用专家积函数(PoE)[13,16]的方法将不同模态的边缘后验分别整合为联合后验

其中:p(z)为先验分布,服从标准高斯分布;qφzx(z | x)与(z | y)为 Q-MVAE模型的共享信息编码器,参数分别为、,服从各向同性的高斯分布.
模型同时、同步针对数据缺失情况下进行训练,以使模型拥有数据缺失情况下的数据推理与生成能力.式(9)与式(10)为模态数据缺失下的概率分布.

对应的边缘概率分布分别为

相应地引入变分分布 q (z,hx|x)与 q (z,hy|y),对式(11)与式(12)进行变换
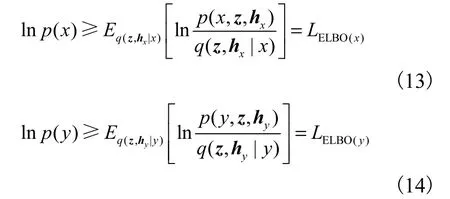
对变分分布进行分解
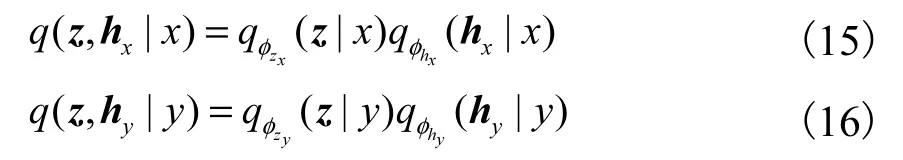
将式(15)与式(16)分别代入式(13)与式(14)中,可分别得到lnpθ( x)、lnpθ(y)的变分下界
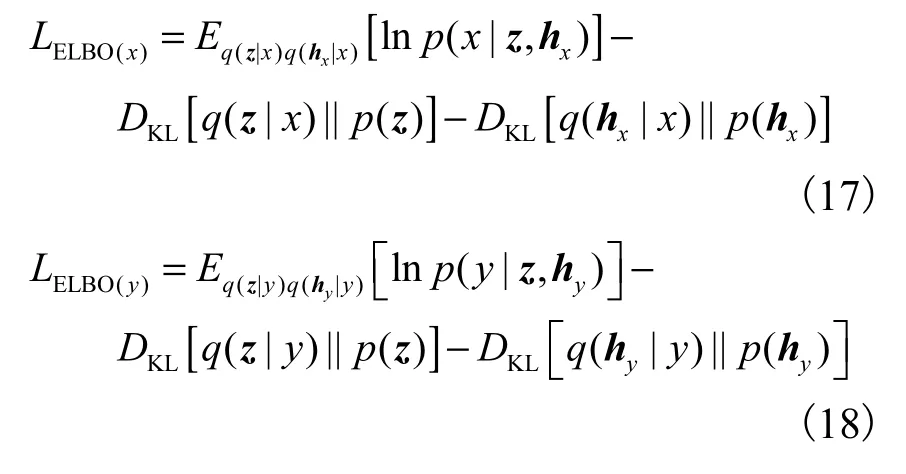
3.3 四元组度量损失
在 VAE框架下,直接最大化式(8)、式(17)、式(18)即可进行模型训练,由于本文提出的 Q-MVAE模型对每个模态数据的共享信息与私有信息进行分开推理表示,因此不同模态的共享隐向量需要在隐空间进行对齐.基于该问题,本文引入四元组度量损失,通过显式地约束不同模态数据样本在隐空间的度量对比关系,使蕴含相同共享信息特征的隐向量之间的度量尽可能小,使蕴含不同共享信息特征的隐向量之间的度量尽可能大.四元组的定义为(x,y,x-, y-),其中x和y表示描述同一对象的两种模态数据样本,蕴含相同的共享信息,x-和y-表示对应的负样本,与对应的正样本x和y蕴含不同的共享信息.以图2为例,图中为两种模态的数字图像,分别是 MNIST[27]手写数字图像与 SVHN[28]街景门牌号数字图像,定义数字类别特征为共享信息,一个四元组可由图中的样本组成,x和 y分别为数字类别为“2”的 MNIST与 SVHN 图像,x-为数字类别为“5”的 MNIST图像,y-为数字类别为“8”的 SVHN 图像,x-和y-也可以是“2”以外的任何数字类别的图像,x-与y-的数字类别关系没有要求,可相同也可不同.

图2 四元组样本示例Fig.2 Samples of quadruplet
四元组度量损失的约束目标为
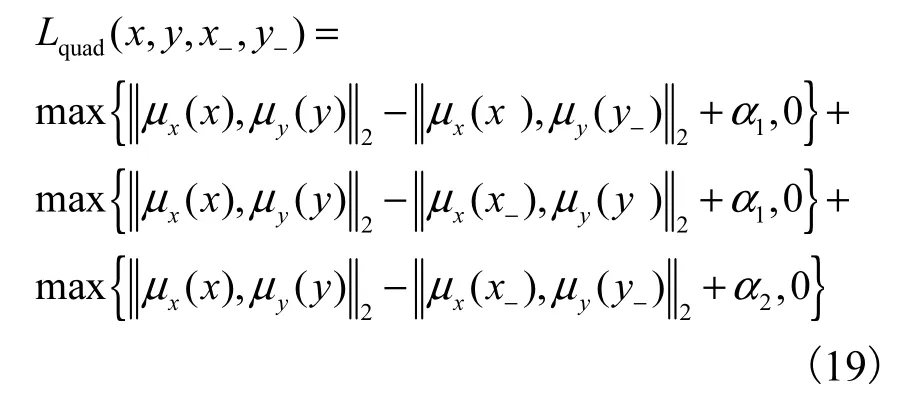
其中μx(x)与μy( y )分别表示取 qφzx(z | x)与 qφzy(z |y )输出结果均值 μ的部分.式(19)右侧的第一项与第二项分别约束正样本对 x和 y之间的度量小于正样本与负样本x-和y-之间的度量,α1为对应超参数;第三项约束正样本对 x和 y之间的度量小于任意两个不同模态数据负样本之间的度量,α2为对应超参数.
3.4 模型最终的目标函数与训练
联合式(8)、式(17)—式(19)可以得到 Q-MVAE模型最终的目标函数为
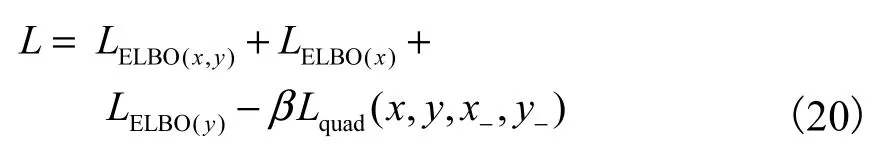
其中β为超参数.模型同时考虑模态数据完整与部分缺失情况下的训练.在模态数据完整情况下,模型对不同模态数据的共享隐变量 z通过PoE进行积函数混合,由于编码网络均为高斯分布,所以混合后仍为高斯分布,其均值与方差的计算具有解析解[13,16],可直接用于模型训练.在模态数据缺失情况下,模型直接使用编码网络 qφzx(z | x)与 qφzy(z | y)的输出结果 z作为共享隐变量 z.对于 Lquad(x,y,x-, y-)部分的训练,需要为正样本对 x和 y选择相应的负样本x-和y-.本文先从数据集中随机选取样本作为负样本,然后利用训练中的模型筛选负样本进行模型训练,最后将模型最终的目标函数整体取负,就可以使用梯度下降方法进行模型训练与优化.
4 实 验
4.1 数据集与实验设置
实验采用多模态数据集 MNIST-SVHN[14]评估Q-MVAE模型的性能.数据集包含 MNIST[27]手写数字图像(分辨率为 1×28×28)、SVHN[28]街道门牌号数字图像(分辨率为 3×32×32)两种模态的数字图像,文献[14]将上述两种模态的每张数字图像与另一种模态相同数字类别的20张图像分别组成拥有相同数字类别的图像对,形成了 MNIST-SVHN数据集,包括1682040对训练样本,300000对测试样本.
在该数据集下,实验训练迭代次数为 10,批大小为 128,隐空间维度为 20,训练中的超参数取值为{α1,α2,β} = { 2 ,0.8,1500},使用 Adam[29]进行训练优化,学习率为 0.0001.对于 MNIST模态图像数据采用全连接神经网络,对于 SVHN模态图像数据采用卷积神经网络,其中卷积核大小为 3×3,卷积步长为2,填充值为 1.
4.2 数据生成
数据交叉生成与转换生成是多模态生成模型的核心能力.由于 Q-MVAE模型将数据的共享信息与私有信息分开推理表示,通过已知的条件模态数据样本输入相应的共享信息编码网络,得到样本的共享隐向量,将其与从目标模态数据的私有隐向量先验分布中采样结合,再输入目标模态数据解码网络,完成数据交叉生成.数据转换生成与交叉生成类似,不同之处在于通过将已知的参考样本输入相应私有信息编码网络,得到私有隐向量,将其与之前获得的共享隐向量结合输入目标模态数据解码网络,完成数据转换生成.
4.2.1 数据交叉生成
数据交叉生成实验包括定性与定量实验,分别对比 MVAE[13]、MMVAE[14]、DMVAE[15]模型,其中DMVAE模型为目前MNIST-SVHN数据集[14]的数据交叉生成与转换生成效果最好的模型之一.定性实验验证对比各模型的数据生成质量与多样性(图3),定量实验验证对比各模型数据交叉生成的准确性(表1).定量评估方法以测试集所有数据为条件样本分别做MNIST到SVHN以及反方向的数据交叉生成,然后将交叉生成的图像送入对应模态数据的图像分类器中进行分类,计算分类结果与条件样本标签匹配的准确率.其中,图像分类器指预先训练好的MNIST与 SVHN图像分类器.为了确保公平性,本文实验采用文献[14]公开的图像分类器.

图3 交叉生成实验效果Fig.3 Cross generative results
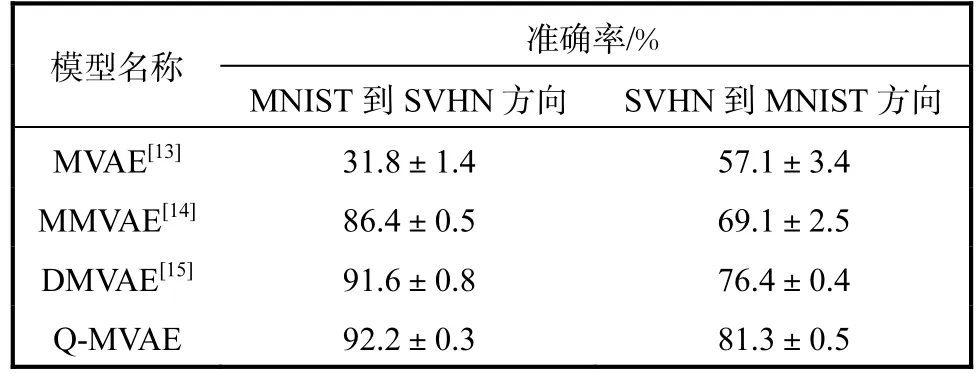
表1 数据交叉生成准确率实验结果Tab.1 Experiment results of data cross generative accuracy
图3的生成效果图中,每张第1行为已知的条件模态样本,其余行表示生成的缺失模态样本,具有随机的私有信息,每一行的共享隐向量从对应条件模态样本中抽取且与私有隐向量相同.图3(a)—图3(d)为从条件 SVHN模态数据生成 MNIST模态数据的生成结果,结果表明:本文的Q-MVAE模型可以生成具有随机风格,且与已知样本相同数字类别的清晰图像.其中图3(a)中第 1行生成数据具备较粗字体的风格,第 4行生成数据具备较为纤细字体的风格,第7行与第10行生成数据分别具备字体前倾和后倾角度的风格,并且每张生成图像与对应条件样本的数字条件均相同.各对比模型中,DMVAE模型也可以较为准确地生成具备随机风格的图像,如字体粗细与字体角度,但是其生成的图像中部分图像数字难以辨认类别,如图3(b)的第 3列与第 9列的部分生成图像.MMVAE模型和 MVAE模型的生成图像中仅有部分与条件样本数字类别相同,生成的图像也较为模糊,甚至不完整.图3(e)—图3(h)表示从条件MNIST模态数据生成SVHN模态数据的实验效果,结果表明:本文的 Q-MVAE模型可以生成统一字体与背景风格的图像.图3(e)中的第 3行与第 6行的图像背景左侧嵌入了白色的粘连阴影,第8行的数字图像有蓝色和白色的背景.这些较为复杂的背景正是SVHN数据集的图像风格特征,DMVAE模型也可以将相应的风格特征嵌入生成图像中,MMVAE模型与 MVAE模型不仅生成的数字模糊,而且没有很好地抽取生成SVHN的风格特征.
表1展示了 Q-MVAE的数据交叉生成准确率,实验均在不同随机种子下进行了 5次独立实验.由表1可知:本文模型在两模态不同方向上的交叉生成准确率均超过了其他模型,其中从 SVHN到 MNIST方向的交叉生成准确率比目前效果最好的 DMVAE模型提升了 4.9%,这与图3的定性生成效果相吻合.根据已知的条件样本,Q-MVAE可以很好地抽取其共享信息,并且能够准确地生成拥有该共享信息的其他模态数据.
4.2.2 数据转换生成
数据转换生成实验为定性实验,对比模型为DMVAE模型[15],转换生成实验效果如图4所示.图4中每张效果图的第一行为已知的条件样本,提供共享信息(本实验为数字类别信息),第一列为已知的参考样本,提供私有信息(本实验为字体与背景等风格信息).从图4中可以看出,Q-MVAE模型可以准确抽取图像的公有与私有信息,并且可以进行相应的转换生成,生成质量更为清晰.

图4 转换生成实验效果Fig.4 Translation generative experimental results
图4(a)为MNIST到SVHN方向的转换生成,生成的图像均准确地从条件样本中抽取了数字类别信息,同时准确地抽取了参考样本的字体风格与颜色背景信息.值得注意的是:图4(a)第3行参考样本中数字右侧背景有粘连的白色背景特征被模型准确地抽取到且成功嵌入生成图像;第4行参考样本原始图像比较模糊,模型将该图像的模糊当作了私有信息进行抽取并成功生成了相似风格的图像.DMVAE模型也基本可以进行准确的共享私有信息抽取与生成,但是图4(b)第 3行生成效果中并没有准确抽取参考样本的私有信息,而生成的是具有不同风格的特征且较为模糊的图像.图4(c)为 SVHN到 MNIST方向的转换生成.图4(c)第 2行与第 4行成功抽取到参考样本的相对粗壮字体风格信息,第3行、第7行与第10行成功抽取到参考样本的数字角度信息,并且都嵌入生成图像中,整体生成质量清晰准确.图4(d)的DMVAE模型生成质量较为模糊,第8列生成图像没有准确抽取共享信息,其将条件样本的数字类别“6”错误地转换生成为数字类别“9”.
4.3 多模态数据分类
概率生成模型对数据的表示隐向量可被用于数据分类等下游任务[2].为了验证 Q-MVAE模型在下游任务中的性能,在 MNIST-SVHN多模态数据集上进行了对比实验,比较模型的多模态数据分类能力.将训练集所有样本输入模型的共享信息编码网络,经过专家积函数混合之后得到共享隐向量,与训练集样本对应的数字标签训练一个线性分类器,然后将测试集所有样本分别输入共享信息编码网络,得到测试集数据样本的共享隐向量,使用上述训练好的单个线性分类器可以同时对不同模态数据进行分类.多模态数据分类准确率实验结果见表2.线性分类器是一个单层神经网络,其参数与文献[14]的公开代码一致,输入维度为20,输出维度为10.

表2 多模态数据分类准确率Tab.2 Experiments of multimodal data classification accuracy
从表2可以看出,Q-MVAE模型的分类准确率均高于各对比模型.Q-MVAE模型仅通过单模态数据就可以进行高准确率分类,在两模态数据同时提供的情况下,模型分类准确率较仅提供 SVHN模态数据有明显提升,但略低于仅提供 MNIST模态数据.这表明模型从两个模态数据中抽取了比单模态数据更多用于分类的信息.同时,MNIST模态数据的共享信息特征相较于 SVHN模态数据更易被抽取,从两个模态抽取的共享信息进行融合之后,可以较大程度提高 SVHN的分类准确率,但是从 SVHN数据中抽取的误差信息也会微弱地影响从MNIST数据中抽取相对准确的信息.因此,Q-MVAE模型可以很好地抽取表示不同模态数据的共享信息,使用单个线性分类器同时对不同模态数据分类均取得高的准确率,也表明本文提出的四元组度量损失对不同模态的共享隐向量在隐空间进行了很好的对齐.
4.4 解耦表示生成
通过设计对私有信息的解耦表示与生成实验,验证模型对私有信息的抽取与表示性能.基于 MNISTSVHN数据集下的交叉生成实验,设计将私有隐向量除某维度之外的所有维度值不变的前提下,对该维度的值进行线性微量变化,观察图像生成效果.图5为在两个方向上的交叉生成,其中对私有隐向量中的10个维度进行逐维度线性微调数据生成.

图5 有解耦特性的交叉生成实验效果Fig.5 Experiments of cross generative with decoupling feature
以图5(a)中的第 1行生成图像为例,该行图像为固定私有隐向量除第1维度以外所有维度的值,并将第 1维度的值在-5~5之间等间距取 20个值分别生成第 1行的20张图像,即生成每一行图像的私有隐向量只有第1维度的值有微小差别,以下各行为依次改变其他单一维度的值生成的图像,以此观察对隐向量生成因子的解耦表示与生成.从图5(a)中可以看出:第1行生成的数字大小随着私有隐向量第1维度值的微量增大而变大,可以认为私有隐向量第 1维度解耦地学习到字体大小的生成因子;第5行的数字角度随着私有隐向量第 5维度的改变由数字角度后倾慢慢变为数字角度前倾,可以认为第5维度学习到控制数字角度的生成因子;第 10行可以被认为学习到背景明暗的生成因子.从图5(b)中看出:第1行对应隐向量学习到数字角度的生成因子,第3行对应隐向量学习到数字字体粗细的生成因子,以下各行则学习到字体胖瘦与不同字体风格的生成因子.
通过上述实验可以看出,对多模态数据进行共享信息与私有信息解耦表示,并显式地约束共享信息进行对齐,可以使模型在多模态交叉生成、转换生成与数据分类等下游任务中取得更好的效果.此外,解耦表示生成实验还使模型展现了对图像风格信息等更细致生成因子推理的潜力.
5 结 语
针对多模态数据生成问题,提出了一个基于四元组度量损失的多模态变分自编码模型 Q-MVAE.该模型在对多模态数据的共享信息与私有信息解耦表示的架构下,引入了四元组度量损失,显式地约束模型训练时在隐空间对共享隐向量进行对齐,有效提高了模型的数据表示与生成能力.相关对比实验证明了 Q-MVAE模型可以有效学习、抽取与表示多模态数据的共享信息与私有信息,并能利用这些表示隐向量进行数据生成与重构,也能进行多模态数据分类等下游任务.Q-MVAE模型通过逐维度操控私有隐向量进行风格渐变的数据生成展现了对数据的解耦表示潜力.在保证模型数据生成质量与多样性的前提下,如何更好地对多模态共享信息与私有信息生成因子进行解耦表示与生成是下一步的研究重点.

