基于STM32微控制器的电容式微位移测量系统的设计

刘玉良，叶扬扬，孙维一，王勇斌，陈建梁，杨伟明

(天津科技大学电子信息与自动化学院，天津 300222)

现代精密测量技术一直是现代工业发展的基础，已经成为衡量各国科技发展水平与工业化发展程度的重要标志.微位移测量技术作为精密测量技术的一个重要分支，也越来越受到人们的重视.无论是航空、航天、大飞机、高铁等尖端产业的生产制造，还是芯片、通信光纤、高端医疗设备等民生产品的加工制造，都依赖于位移测量的精度，测量精度的高低在优化生产流程、提高产品质量的过程中发挥了至关重要的作用[1].

微位移传感器是微位移测量系统中的核心器件，根据传感原理不同可以分为激光式、电感式、电涡流式和电容式等类型[2].与激光式、电感式等微位移传感器相比，电容式微位移传感器具有结构简单、成本低、抗干扰能力强、分辨率高、动态特性好等优点，在精密测量与控制领域得到长足的发展，并且呈现出高精度、智能化、便携化和模块化的发展趋势[3–4].

电容式传感器按照其传感特性分为3类：变面积型传感器、变介电常数型传感器与变极距型传感器.变极距型传感器非线性误差较大，不适合较大量程直线位移的测量，而变电介质型传感器常用于特定参数的测量.变面积型电容传感器的实际输出特性在较大量程范围内是线性的，且传感器灵敏度是常数，多用于测量直线位移、角位移、尺寸等参量[5–6].然而，主流的电容式位移传感器的量程普遍偏小，这类传感器中具有代表性的产品为德国 ME公司的NCDT6100型单板式电容位移传感器，它的最大量程为 2mm；国内基于电容式传感器的微位移测量系统的精度能够达到10μm，最大量程为2mm.由于这类传感器探头部分采用板级结构，实际输出特性的线性度较差，传感器连接的寄生电容很容易与传感器本身电容同级，甚至更高[7–8]，从而导致量程较小.

为增大传感器的量程，从传感器的探头设计和转换电路出发，结合嵌入式平台，设计了一种基于嵌入式的电容式微位移测量系统.通过探头设计改善量程偏小的问题，并采用双层屏蔽线和数据处理减小寄生电容的影响.为进一步提高测量精度，对测量的数据进行线性拟合，得出更精确的数学模型.

1 系统整体设计

1.1 系统框架

系统以STM32F103ZET6微控制器为主控，该芯片具有处理速度快、功耗低、性能优秀等优点，并且它的可扩展能力强，能够满足不同领域的多种测控系统的需求.其通过IIC总线控制电容测量和转换电路中电容数字转换器AD7747的工作模式，并接收测量数据，将经过数据处理后的数据在液晶显示屏上显示出来.电容测量和转换电路是整个系统的核心部分，其电容数字转换器的CIN(＋)引脚连接电容传感器探头的电极，接收电容传感器的电容梯度信号.系统的整体框架如图1所示.

图1 系统框架图Fig.1 Diagram of system framework

电容测量和转换电路以电容数字转换器为核心进行设计，电容数字转换器中二阶 Σ–Δ型 ADC(模拟数字转化器)分辨率高达 24位，具有转换速率快、精度高的优点.同时，该 ADC降低对信号滤波的要求，取消了信号调理.ADC与三阶数字滤波器组成高精度转换器，将转换后的数字信号写入数据寄存器，最终通过 IIC总线发送到主控芯片.除了转换器之外，电容数字转换器还集成了多路复用器、激励源、CAPDAC(可编程片上数字–电容转换器)、温度传感器、基准电压接口、完整的时钟发生器、控制逻辑校准接口以及IIC兼容串行接口，能够进一步提高基于电容传感器测量系统的精度.电容测量系统的原理如图2所示.

图2 电容测量和转换电路图Fig.2 Diagram of capacitance measurement and conversion circuit

由于电容梯度信号属于微小信号，所以在获取目标信号的过程中非常容易受到外界环境(如磁场、温度、湿度)以及机械运动的影响，从而导致连接传感器的寄生电容的变化，这些变化被视为转换结果中的漂移，严重影响系统的精度[9].数据采集电路测量CIN(＋)引脚和大地之间的电容，其中在CIN(＋)引脚和传感器之间的信号路径上，对地的任何电容都包含在电容数字转换器的转换结果中.为降低大地到CIN(＋)引脚信号路径上的杂散电容，利用电容数字转化器的 SHLD引脚进行有源交流屏蔽，将 SHLD引脚连接到屏蔽电缆的屏蔽层，使屏蔽层达到与CIN(＋)引脚激励相同的信号波形，减少杂散电容的影响.引脚信号波形如图3所示.

图3 CIN引脚输出波形Fig.3 CIN pin outputs waveform

增加一个温湿度传感器模块 DHT11，记录实际测量时环境的温度和湿度.尽管电容数字转换器使用了片上晶体管来测量封装芯片内部的温度，但由于芯片自身存在功耗产生自热，所以不能将内部温度传感器作为系统温度传感器.其中，片上温度传感器经Σ–Δ 型 ADC转换为数字信号，输出数值与温度成正比，见式(1).

式中：T为温度转换结果，单位为℃；N为数据寄存器的数值.

1.2 圆筒式电容传感器原理

基于圆筒式电容的测量原理如图4所示，内圆柱接 CIN(＋)引脚，外圆筒接地，这样，内圆柱和外圆筒之间就会存在电势差U.

图4 测量原理示意图Fig.4 Schematic diagram of measuring principle

电容梯度理论模型为

式中：C为电容，ε为空气的介电常数，S为内圆柱和外圆筒的相对面积，d为内圆柱和外圆筒的间距.

根据电容梯度理论模型，将位移量转换为相对面积变化量，得到圆筒式电容梯度理论模型.假设内圆柱和外圆筒之间相对初始重叠长度为 h0，外圆筒内半径为R，内圆柱外半径为r，初始电容为C0，则电容Cx和位移x的关系式为

通过式(3)可以得出圆筒变面积型电容传感器探头的理论特性，但是由于环境(比如温度、湿度)因素、边缘效应以及寄生电容的影响，传感器的实际特性和理论特性往往存在偏差，如图5所示.由图5可以看出，实际输出曲线在一定范围内线性度较好，可以通过改进探头结构以及屏蔽寄生电容来改善系统量程[10].

图5 探头输出特性曲线Fig.5 Probe output characteristic curve

1.3 电容传感器设计

电容传感器的传感部分由外圆筒和内圆柱组成，结构如图6所示.外圆筒接地，最外层包裹一层绝缘材料，防止电磁干扰；内圆柱作为电容信号的输入端，连接电容测量和转换电路[11].

图6 探头示意图Fig.6 Diagram of probe

内圆柱相对于外圆筒进行同轴的上下直线运动，产生与外圆筒的相对重叠面积呈线性关系的电容梯度信号(即电压信号)，经过电压测量电路和转换后得出具体电容梯度.

电容数字转换器最大电容测量值为 8.192pF，根据式(2)可以计算传感器探头所需的最大有效面积.

在 d＝0.5mm、C＝8.192pF时，通过计算可知传感器探头所需的最大有效面积Smax＝462.8mm2.

根据电容梯度仿真和计算结果，设定外圆筒的内半径 R＝8.6mm、内圆柱的外半径 r＝8.1mm、内圆柱高 h＝15mm，根据这些数据可计算出本文所设计的装置所能提供的最大有效面积S′max.

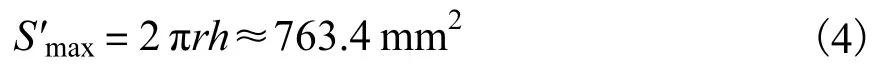
该探头的设计能够满足系统满量程时对电容测量的要求，使其电容值与位移成正比.

1.4 软件设计

整个系统的软件设计核心是主控系统对电容数字转换器的控制和数据接收.电容数字转换器支持IIC串行接口，SCL(时钟线)和 SDA(数据线)通过总线将所有的寻址、控制和数据信息一次一比特传送到微处理器 STM32F103.微处理器向电容数字转换器发送起始字节，0x90和0x91分别表示对电容数字转换器进行写和读的操作，紧接着发送需要写的寄存器地址[12]，具体流程图如图7所示.

图7 软件流程图Fig.7 Flow chart of software

当在起始字节中选择写时，起始字节后面的字节总是寄存器地址指针字节，它指向电容数字转换器上的一个内部寄存器.地址指针字节自动加载到地址指针寄存器中，由电容数字转换器确认.在地址指针字节确认后，停止条件、重复启动条件或另一个数据字节可以从主站跟进.停止条件的定义是 SDA上的低电平到高电平的转换，而 SCL保持高电平.如果电容数字转换器遇到了停止条件，它将返回到空闲状态，地址指针被重置为0x00.

当选择读时，当前由地址指针寻址寄存器的数据将传送到 SDA线上.然后由主设备将其时钟输出，电容数字转换器等待主设备的确认.如果收到主设备的确认，地址自动增量器会自动增量地址指针寄存器，并将下一个寻址寄存器内容输出到 SDA线上，传送给主站.如果没有收到确认，则电容数字转换器返回空闲状态，地址指针不增.

2 实 验

2.1 实验平台搭建

使用分辨率为1μm的螺旋测微仪进行系统的微位移标定.根据探头和螺旋测微仪的形状和大小设计专用的测试平台.整个测试平台由 1个电容传感器、3个3D打印部件、1个螺旋测微仪及若干铜柱组成.3D 打印部件用 SOLIDWORKS软件设计[13]，部件图如图8所示，测试平台实物图如图9所示.

图8 测试平台3D打印部件图Fig.8 3D printing part drawings of test platform

图9 测试平台实物图Fig.9 Physical picture of test platform

部件 a用来固定探头外圆筒，位于测试平台上层.部件 b用来固定螺旋测微仪，位于测试平台的下层.部件a和部件b上都有4个条形固定孔，并且保持垂直，可以保证 a、b两个部件只能进行二维运动，进而在调整内圆柱和外圆筒的相对位置时，电容传感器的内外圆形电极同轴.部件c用于嵌合电容传感器内电极和螺旋测微仪的测微螺杆，使内电极随着螺旋测微仪与外电极做相对运动来改变电容传感器梯度.

2.2 电容梯度测量及数据处理

为研究电容传感器内外电极的相对位移和电容梯度变化的关系，需要进行二维标定实验.电容式位移传感器的内电极和螺旋测微仪螺杆连接在一起，旋转螺旋测微仪即可改变电容式位移传感器的内电极在外电极中的位移 x，进而使电容传感器的电容发生改变，电容数据经过数据采集电路在嵌入式系统中显示出来[14].

本文设计的电容传感器的电容值满量程是8.192pF，考虑到传感器和周围器件存在较大的寄生电容，这会导致最终测量的结果会大于其量程，所以使用电容数字转换器的片上可编程CAPDAC平衡寄生电容.CAPDAC可以理解为连接到CIN(＋)引脚内部的负电容，电容输入和输出之间的关系为

式中：C′为平衡过后的电容， ′′C为可编程平衡寄生电容.

首先进行精度实验，实验选择两个不同测量区间进行，具体实验步骤为：调整内外电极至不同测量区间初始位置，并通过可编程 CAPDAC平衡寄生电容；转动螺旋测微仪，每次转动10μm，在连续一段时间内记录 10组电容数据信号；不断重复上一步骤，在每个测量区间内共测得 200组数据.最终测量得到的数据见表1和表2.

表1 精度实验前置区间的部分数据Tab.1 Partial data of pre-interval of precision experiment

表2 精度实验后置区间的部分数据Tab.2 Partial data of post-interval of precision experiment

使用MATLAB软件对位移和电容数据进行最小二乘多项式拟合[15]，x表示各测量区间增量为 10μm的位移，y表示测量的电容，所得拟合曲线如图10所示.

图10 精度实验的拟合曲线Fig.10 Fitting curve of precision experiment

使用决定系数 R2对拟合后的曲线进行评价，决定系数用来表征拟合结果的好坏，其正常取值范围为[0，1]，越接近 1，表明这个模型对数据拟合的效果越好.本文拟合所得方程的决定系数分别是 R2＝0.9998(前置区间)和 R2＝0.9994(后置区间)，决定系数均大于 0.9，表明该测量系统在 10μm 精度上，自变量与因变量具有很高的相关性.

在完成精度实验后，进行电容–位移标定实验，具体实验步骤为：调整内外电极至初始位置 0mm，并通过可编程 CAPDAC平衡寄生电容；转动螺旋测微仪，每次转动 0.1mm，在连续一段时间内记录 10组电容信号数据；不断重复上一步骤，实验共测得 47组有效数据.最终测量得到的部分数据见表3.

使用MATLAB对位移和电容数据进行最小二乘多项式拟合，x表示位移，y表示测量的电容，最终拟合曲线如图11所示.

图11 电容-位移拟合曲线Fig.11 Capacitance-displacement fitting curve

使用决定系数 R2对拟合后的曲线进行评价.拟合后得到决定系数 R2＝0.99867，决定系数大于 0.9，表明该测量系统的量程能够达到 4.6mm，且在此量程内变量与因变量具有很高的相关性.

3 结 语

为提高电容微位移测量系统的量程和精度，从 3个方面进行改进：(1)设计了内圆柱和外圆筒两部分变面积型传感器探头，提高电容梯度与位移增量线性度；(2)改进转换电路设计，降低寄生电容对测量系统的影响，提高系统分辨率；(3)对数据进行拟合处理，建立数学模型，进一步提高测量精度.实验表明，测量系统量程达到 4.6mm，精度为 10μm，扩大了测量范围且提高了精度.