基于改进相移法的煤田地震瑞利波资料处理

李欣欣，李江，刘军，沈鸿雁

(1.西安石油大学 地球科学与工程学院，陕西 西安 710065；2.西安石油大学 陕西省油气成藏地质学重点实验室，陕西 西安 710065；3.中国石化地球物理重点实验室，江苏 南京 211103；4.中煤科工集团西安研究院有限公司，陕西 西安 710077)

0 引言

瑞利波是一类沿地球表面传播的地震波，其质点在竖直平面内振动，在近地表的浅部其质点振动的轨迹为“逆进”的椭圆[1,2]。瑞利波的能量衰减较穿透地球内部的体波更慢，在垂向地震记录中有较强的振幅和较高的信噪比，因此利用其进行地下结构探测具有高效便捷和抗干扰能力强的优势[3]。早期的瑞利波探测方法利用两道检波器采集信号，然后通过计算两道之间不同频率瑞利波的相位差获得频散曲线，并反演下方地层的速度结构[4]。这类方法由于仅有两道数据，若记录中含有较强的反射波、折射波以及噪声信号时，计算的相位差会包含很大的误差，导致最终的探测结果不准确。因此研究人员发展了多道面波分析(multichannel analysis of surface waves)方法[5]，该方法利用多个检波器采集瑞利波信号并进行处理，相比于两道面波方法极大地提高了频散曲线计算的准确性和稳定性，且能够同时获得基阶和高阶模式的频散曲线，为后续反演处理提供了更多的约束，提高了勘探的质量，因此多道瑞利波方法在煤层采空区探测[6,7]、工程勘察[8,9]、油气地震资料静校正[10,11]等不同领域的地下结构探测中获得广泛的应用。近年来快速发展全波形面波成像方法能够直接从时间域多道面波(瑞利波或勒夫波)波形记录反演地下结构，虽然在理论上可以免去频散曲线的计算，但是在实际应用中成像的质量高度依赖于反演的初始模型，需要借助频散曲线建立较为合理的初始模型[12-14]，并将频散曲线作为约束因子引入全波形反演计算，以提高反演过程的稳定性与收敛性[15]。因此不论对于常规的多道面波分析方法还是全波形面波反演方法而言，获得准确的频散曲线都是瑞利波勘探中的关键所在[16-19]。

针对多道面波频散曲线计算这一个关键问题，目前已有诸如F-K变换[20]、相移法[21]、τ-p变换[22]、倾斜叠加[23]、高分辨率线性拉东变换[24]等各类方法，其中相移法由于对占主导的基阶模式瑞利波的频散能量成像效果较好[25]，在实践中得到广泛的应用。然而当采集数据中波场较复杂或有效信号信噪比较低时，相移法生成的瑞利波频散能量会受到影响，导致提取频散曲线的精度降低，因此本文提出一种改进的相移法对数据进行处理。

1 方法原理

相移法通过傅里叶变换生成频散能量谱，使得多道记录中不同频率成分的瑞利波相互分开。频散能量谱包含相位谱和振幅谱两部分，瑞利波的走时信息包含在相位谱中，振幅衰减、球面扩散等信息则包含在振幅谱中。通过对相位谱和振幅谱进行处理，就可以获得瑞利波的频散曲线，本文对该方法进行改进，现将原理介绍如下。

1.1 相移法

多道地震记录可视为空间-时间域的二维信号d(x,t)，其中x表示偏移距，t表示记录时间，对该信号沿时间轴做傅里叶变换可得：

，

(1)

上式计算得到的频谱D(x,f)可以表示为振幅谱和相位谱的乘积：

D(x,f)=ph(x,f)A(x,f)

，

(2)

式中ph(x,f)表示信号的相位谱，A(x,f)表示信号的振幅谱。若将相位谱利用e-iΦx表示，则上式可写为：

D(x,f)=e-iΦxA(x,f)

，

(3)

式中Φ=2πf/v(f)，v(f)为随频率变化的相速度。若将某一频率的瑞利波经过φ相位移动并进行振幅归一化，然后沿着偏移距方向叠加，则可由式(3)得：

，

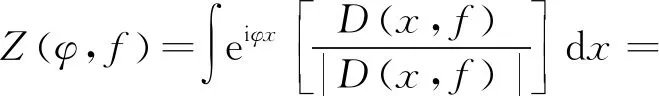
(4)

由式(4)可知，对于给定频率f，如果满足：

，

(5)

则Z(φ,f)将会有一个极大值，那么根据Z(φ,f)谱上的极大值点就可以确定该极大值点对应的φ值。因此，在计算得到Z(φ,f)后，可利用式(5)将f-φ域的Z(φ,f)能量图的每一个能量点所对应的φ值换算为v值[25,26]，即可获得Z(v,f)，再将Z(v,f)绘制在f-v域坐标系中，即可得到f-v域的频散能量图，进而提取频散曲线。

1.2 改进的相移法

实际中采集的数据由于包含噪声和各类型波场，利用相移法计算得到频率谱后，其中的瑞利波能量受其他信号能量干扰，不易区分识别，且频散能量条带的收敛性和聚焦性较差，使得提取的频散曲线准确性降低，甚至在部分频段，瑞利波的频散能量受到压制导致无法获取频散信息。因此本文提出一种改进的相移法对瑞利波频散曲线进行提取，由于瑞利波频散信息包含于相位谱中，而振幅谱表示的是不同成分信号的能量强度，因此我们对相移法生成的频散能量谱中的振幅分量进行改造，同时保持相位谱不变，就可以达到改善瑞利波频散能量收敛性和聚焦性的目的，实现对频散曲线的准确提取。

根据上文所述我们将相移法计算得到的频散能量谱记为Z(v,f)，对Z(v,f)谱上每个能量点的振幅数值进行幂次方运算，且幂值n为大于1的整数，则有：

Zn(v,f)=[Z(v,f)]n,n>1

，

(6)

其中Zn(v,f)为幂运算后得到新频散能量谱，由于经过幂运算，Zn(v,f)中每一点的振幅相对于Z(v,f)都获得了增大，但是并未改变利用式(4)计算Z(v,f)的φ值，因此求幂只针对振幅谱，不会改变Z(v,f)中的相位信息。与此同时，由于经过n(n>1)次幂运算，Z(v,f)中不同点之间的振幅值差异得到扩大，那么在求得的Zn(v,f)中，瑞利波的频谱振幅得到相对增强，并且频散能量条带的收敛性和聚焦性得到改善，进而使频散曲线的提取更加精确。

我们以图1为例具体说明求幂运算的作用，首先提取频散能量谱上某个频率截面上的振动曲线，如图1a为某实际数据的频散能量谱上15 Hz频率处的振幅谱曲线，由图中可见该频率处频谱能量有多个峰值，且不同峰值之间差异较小，其中在约300 m/s处最大振幅为0.459，其右侧的次级振幅为0.276，主次振幅值之比为1.66；图1b为经过n次幂(n=4)计算后的曲线，由图可见约300 m/s处的曲线峰值得到相对加强，其他峰值相对减弱，使得主峰值更加突出，处理后的最大振幅值0.045，次级振幅为0.0058，主次振幅值之比为7.76。

a—原始多峰振幅曲线；b—经过4次方幂运算处理后的曲线

2 模拟数据分析

我们模拟一组地层的理论数据，采用高阶交错网格有限差分和PML吸收边界的方法[27]对理论模型的弹性波场进行数值模拟计算，模型地层参数由横波速度vs、纵波速度vp、密度ρ和层厚度h组成。具体模型参数见表1，模型大小设置为80 m×50 m，震源为主频25 Hz的雷克子波，震源与检波器最小偏移距为5 m，设置51道检波器接收，道间距1 m，采样间隔0.5 ms，采样长度0.5 s。在模拟数据中加入随机噪声，此外数据中也包含反射波、折射波等干扰波场。

表1 理论模型地层参数

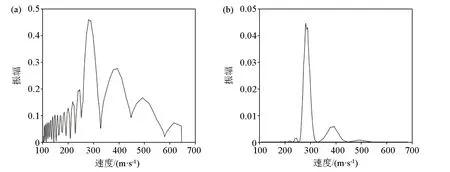
图2a为加入白噪声的模拟数据结果，利用相移法和改进的相移法分别对这组数据进行处理，从炮集记录中可以看到较强的噪声信号以及初至波同相轴，图2b为常规相移法计算生成的频散能量，图中可见清晰的面波频散能量条带，在面波能量条带两侧也显示出噪声及其他类型波场的能量团，根据给定模型计算出的理论相速度频散曲线(图2b中的点状曲线)，我们可以识别出频带范围较窄的部分高阶模式面波的频散能量，由于煤田地震资料中的面波以能量较强的基阶模式为主，因此本文主要针对面波基阶模式频散曲线的提取技术进行研究。

图2c为利用改进的相移法对模拟数据进行处理后生成的频散能量图，与图2b对比可以看出基阶模式面波能量更加收敛，频散谱宽度变窄，在实际数据处理中，能够更加准确地从频散谱的峰值提取频散曲线；与此同时，噪声及其他类型波场(初至波、高阶面波等)在能量谱中受到了较好的压制，使得基阶面波能量更易识别。

a—模拟地震数据；b—常规相移法生成的频散能量；c—改进的相移法生成的频散能量

3 应用实例

以鄂尔多斯盆地南部黄土塬某研究区的煤田地震勘探资料为例，利用改进相移法对其进行处理。研究区表层发育巨厚、干燥、疏松的黄土层，地震激发和接收条件较差，导致地震资料干扰波发育、静校正问题突出、高频吸收衰减严重、资料分辨率及信噪比较低。一般情况下，黄土层的纵波速度为400～1 800 m/s，横波速度为200～700 m/s，且速度、密度随深度增加连续变化，常规的反射、折射等勘探方法难以对巨厚黄土层的内部结构进行有效探测，为煤田地震勘探资料的后续处理带来较大的困难。

本例中的地震数据通过布设396道垂向检波器组成的接收排列采集，检波器的自然频率为10 Hz，道间距10 m，每道采样点数为2 001个，采样间隔为1 ms。激发采用中间放炮的方式，炮点在排列中不同位置处激发，本研究利用资料中连续采集的41炮记录，其中首炮位于184道检波器位置处，然后炮点向排列增大方向移动，炮间距30 m(由于研究区地表条件限制，部分相邻炮间距为20 m或40 m)。

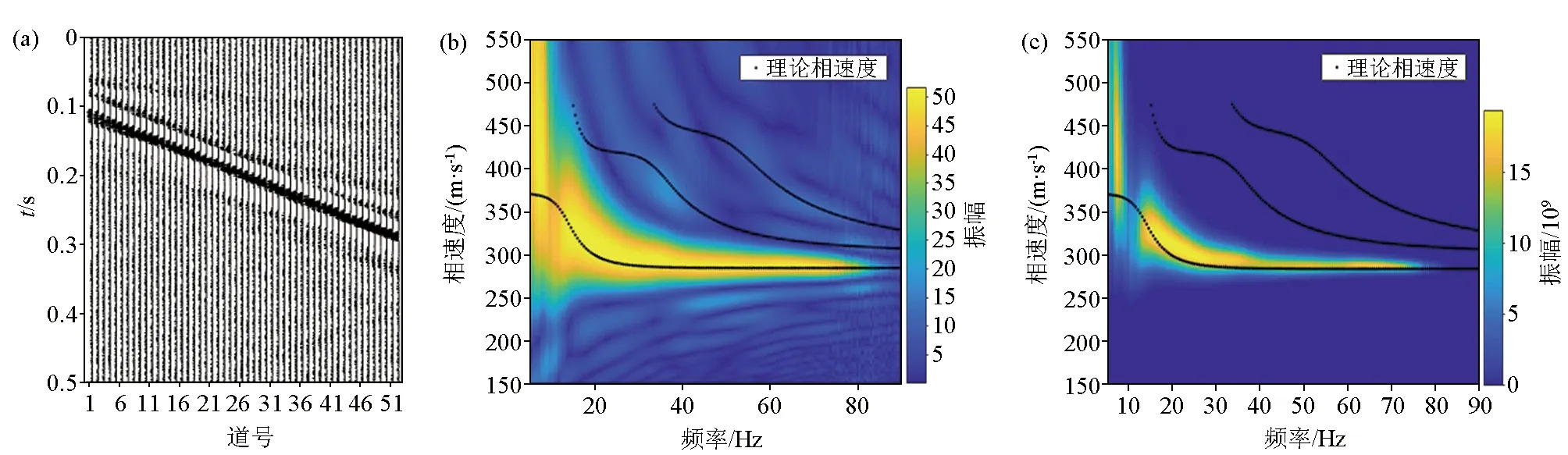
图3a为采集的第1炮数据的160～360道地震记录，炮点位于184道位置处，从记录上能够看到清晰的面波、反射波、直达波以及折射波信号。我们从中抽取炮点右侧25道(186～210道)瑞利波记录较完整的采集道(图3b)，对其进行处理。

a—第1炮160～360道记录；b—第1炮186～210道记录

3.1 频散测量

图4a为利用常规相移法的生成的能量谱，谱中可见两个较强的能量团，图4b为利用改进的相移法生成的能量谱，谱中仅有一个明显的能量条带，即为瑞利波频散能量，相比于常规相移法生成的结果，改进相移法生成的能量谱中其他类型波场及噪声能量谱均得到了压制，且瑞利波的能量条带更加收敛，峰值得到增强，在提取频散曲线时，能够提高各频点对应的相速度的识别精度，我们对该能量条带上不同频率处峰值点的横纵坐标进行提取，就得到了各个频率对应的面波相速度值。

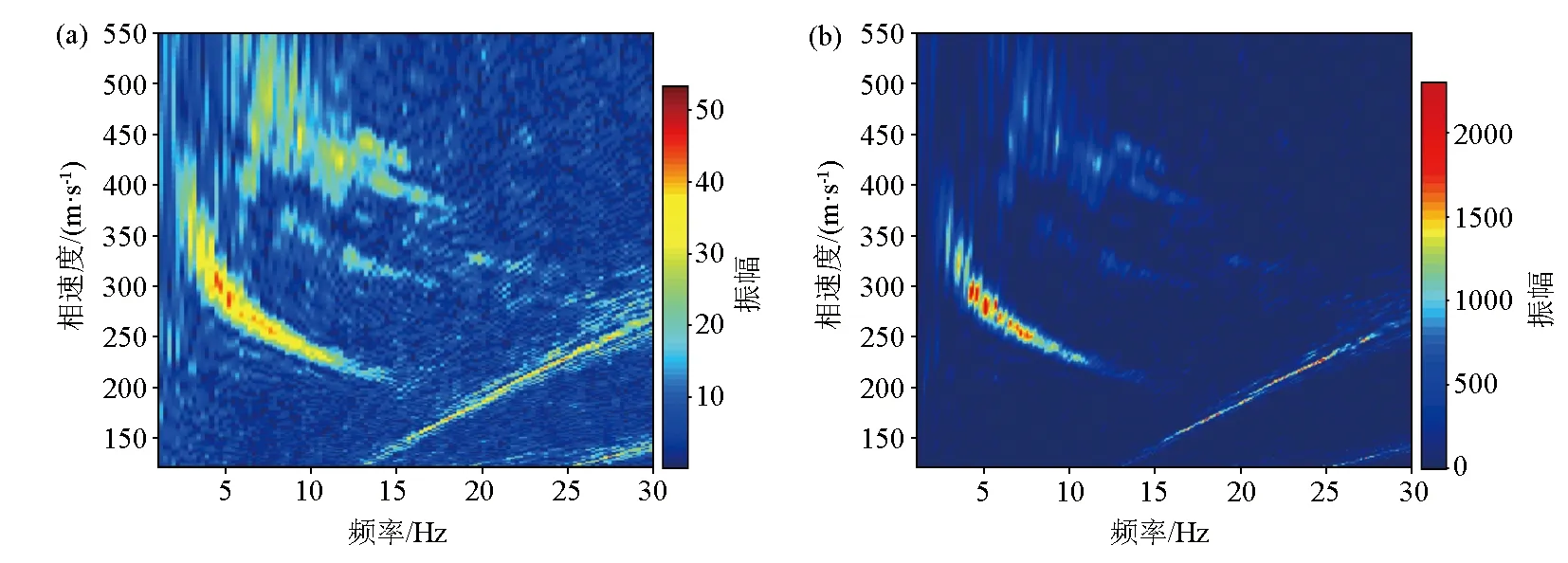
图4 常规相移法(a)和改进的相移法(b)生成的频散能量谱

3.2 横波速度反演

利用改进的相移法对41炮数据分别进行处理，提取了不同测点位置处的频散曲线，然后对频散曲线进行反演，获得不同测点下方地层的横波速度结构。图5为第17炮数据的处理结果，包括从该数据中提取的频散曲线(图5a中蓝色虚线)，以及对该频散曲线进行反演获得的测点下方的横波速度结构(图5b中红色折线)。本研究采用阻尼最小二乘方法进行反演，反演的初始模型由频散曲线估计得到，初始模型见图5b中的蓝色折线所示，最终反演模型对应的频散曲线见图5a中红色实线所示，其与观测频散曲线吻合良好。

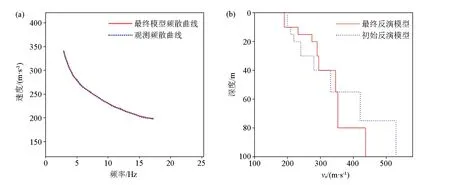
图5 第1炮记录的频散曲线(a)及第1炮测点下方的地层横波速度结构(b)

3.3 2D剖面

经过频散测量和反演处理后，得到各测点的横波速度结构，然后通过插值将所有测点的横波速度结构联合，生成了研究区内一条1.2 km长的横波速度剖面(图6)。剖面图显示了测线下方80 m深度范围内的地层横波速度变化情况，地层横波速度值总体在150～550 m/s范围内，其中0～15 m深度范围横波速度低于250 m/s，主要为松散的土壤沉积物，在大约15～50 m深度范围，横波速度为250～350 m/s，在大于50～70 m深度范围，横波速度为350～500 m/s，主要成分为经过压实的较坚硬黄土，在大于70 m深度，地层的横波速度大于500 m/s，推测为较密实的碎石土沉积。

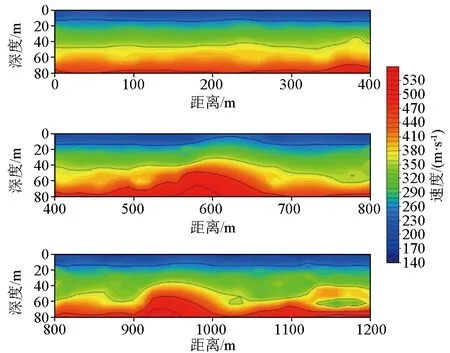
图6 研究区2D横波速度结构剖面

4 结论

1)本文基于改进的相移法对煤田地震中的瑞利波资料进行处理，在求取频散能量谱时引入求幂运算，对谱上各数据点的振幅进行二次处理，使得瑞利波的能量得到增强，其他类型波场及噪声的能量受到压制。经过处理，瑞利波的频散能量条带的收敛性和聚焦性显著改善，有效地提高了提取频散曲线的精度。

2)利用改进相移法对某研究区煤田地震资料中的瑞利波进行了处理，获得研究区的二维横波速度剖面，建立了覆盖层模型，结果表明该方法能为复杂波场条件下的瑞利波频散测量提供技术支持，在黄土覆盖区表层速度建模及近地表成像领域具有良好的应用前景。