基于时差定位法的管道多点泄漏定位研究
韩文翔, 章兰珠
(华东理工大学 机械与动力工程学院,上海 200237)
管道作为运输介质的载体,具有经济、安全、不间断性、运输量大等多重优势。在提供便利的同时,由于腐蚀、老化和人为破坏等因素的影响,一旦发生泄漏事故,后果颇为严重,损坏国民经济甚至威胁生命安全[1]。针对管道泄漏的检测已经有示踪法、负压波法、声学检测法等较成熟的检测方法。其中声发射(acoustic emission,AE)技术作为一种具有在线动态监测特点的新型检测技术,可以及时发现管道的早期缺陷,提高检测效率,具有良好的工程实际应用价值[2]。
目前在管道泄漏领域的研究较多集中在单点泄漏场景,利用时差定位法、神经网络等方法可有效解决管道泄漏的定位问题。而真实工况下往往会发生多点泄漏的现象,多点泄漏由于泄漏信号之间的相互干扰给研究带来了一定的难度,目前还没有形成成熟的管道多点泄漏定位方法。高华[3-4]等提出一种改进差分进化算法的管道泄漏定位方法,将采集到的信号经过小波消噪后并根据信号幅值建立改进差分进化算法的目标优化函数,通过对其求解获得泄漏源位置,但是该方法未考虑弯管、变径等工况对信号幅值的干扰。而声发射信号可以避免复杂工况对信号特性的影响,管道在发生泄漏时由于内外压差导致内部介质与外部环境之间的摩擦从而形成高频应力波[5],这种机械波组成的声发射信号与语音信号同为非平稳信号,可借鉴语音信号处理中的盲辨识法应用于管道多点泄漏的检测。盲辨识问题实质上是盲源分离中混合矩阵的估计问题,根据信号源数量与传感器数量之间的关系可分为超定、适定和欠定3种类型[6]。目前该领域的研究热点主要在欠定盲源分离,而超定和适定两种情况下的盲源分离技术相对成熟,本文的研究重点在于利用信号处理技术提取有效的泄漏特征信号并结合盲源分离算法实现管道的多点泄漏源定位,因此选用基于快速独立成分分析(fast independent component analysis,Fast ICA)的适定盲源分离算法。
在盲源分离的应用中,往往将噪声分量当做独立成分分离,考虑到去噪效果和盲源分离后排序未知等问题的限制,本文先对采集信号进行去噪预处理。通过对变分模态分解(variational mode decomposition,VMD)分解后有效模态选取依据的研究提出一种结合互谱的信号去噪算法,并通过试验验证了该去噪方法的有效性和多点泄漏应用的可靠性。
1 基于声发射技术的时差定位原理
声发射技术是近年来得到快速发展的一种动态无损检测新技术,该技术可以在不破坏被检结构的情况下对构件进行全天在线监控,并能对结构中出现的疲劳及失效做出早期预警,具有实时监测、动态监测、覆盖面广等优点[7]。管道发生泄漏时,释放的气体与管道裂口通过摩擦所产生的能量以应力波的形式释放,此过程称为声发射现象,通过传感器对声发射信号的采集和分析可实现管道泄漏的检测。但是由于声发射信号的本身特性及环境因素的影响,需要对采集信号进行适当的分析和处理才能进一步精确确定泄漏点的位置。
在泄漏源定位方面,常采用时差定位法[8],其原理如下
(1)
式中:x为被检测管道泄漏点的位置,即泄漏点到上游传感器距离,m;Δt为泄漏信号到达两个传感器的时间差,s;v为泄漏信号在管道中的传播速度,m/s。
由于两传感器之间的距离是已知的,因此只需知道Δt便可得出泄漏源的位置。互相关函数是计算两个信号相关性的常用方法,根据互相关时域分析图中最大相关峰值进而计算得到上,下游有效泄漏信号到达两个传感器的时差Δt。
2 泄漏特征信号提取
管道运行过程中环境噪声的干扰会对定位结果造成显著影响,因此有必要先对采集到的信号进行去噪处理,目前信号去噪领域已具很多成熟的算法,例如小波分解、小波包分解等信号处理算法。虽然小波分解在工业中的应用已经有了长远的发展和进步,但是小波基函数的选择和分解层数的确定始终是摆在分析人员面前的问题[9]。为此Huang等[10]提出一种完全基于数据驱动的自适应分解方法——经验模态分解(empirical mode decomposition,EMD),它将信号分解成有限个从高频到低频的固有模态函数(intrinsic mode function,IMF) 和残余分量之和, 能够很好地分析处理非线性、非平稳信号。由于信号中存在间断信号和脉冲干扰等异常事件的干扰,使得EMD 存在模态混叠的问题,这会降低EMD 的降噪效果。基于此,研究人员又陆续发明了集合经验模态分解(ensemble empirical mode decomposition,EEMD),VMD等信号处理算法[11]。
2.1 互谱分析原理
互谱可由互相关函数经傅里叶变换求得从而在频域内描述两信号s1(k)和s2(k)之间的相关性[12]。对s1(k)和s2(k)的相关函数作傅里叶变换得互谱公式如下
Ss1s2(f)=αSss(f)ej2πfτ=αSss(f)ejθs1s2(f)
(2)
式中,Sss(f)为采集信号的自谱。由式(2)可得时间延迟为τ,则相位差为
θs1s2(f)=2πfτ
(3)
在采集信号的频带内,θs1s2(f)与频率成线性关系,斜率为2πτ。互谱的计算公式如下
(4)
式中:S1(f)和S2(f)分别为s1(k)和s2(k)的离散傅里叶变换系数;*为复共轭。
互谱估计常采用Welch平均周期图法表示为
Gs1s2(f)=Gs1s2(f)+jQs1s2(f)
(5)
式中,Gs1s2和Qs1s2(f)分别为共谱密度和正交谱,可得相位谱如下
(6)
将s1(k)和s2(k)的互谱相位谱作差可得互谱相位差谱,差谱值越接近水平表明频率相关性越高。
利用Welch平均周期图法可得S1(f)和S2(f)的自谱Gx1x2(f)和Gx2x2(f),则s1(k)和s2(k)的幅值平方相干函数为
(7)
相干函数可从频域的角度反应两段信号的相关程度,频带的相干函数值越大表明该频段的信噪比越高,因此可根据互谱相位差谱和相干函数估计泄漏特征频带。
试验采用北京软岛科技研发的声发射仪器和实验室搭建的管道装置,在泄漏源上下游两端各放置一个声发射传感器,选用2.5 M的采样率,计算两段信号的互谱相位差谱和相关函数如图1所示。
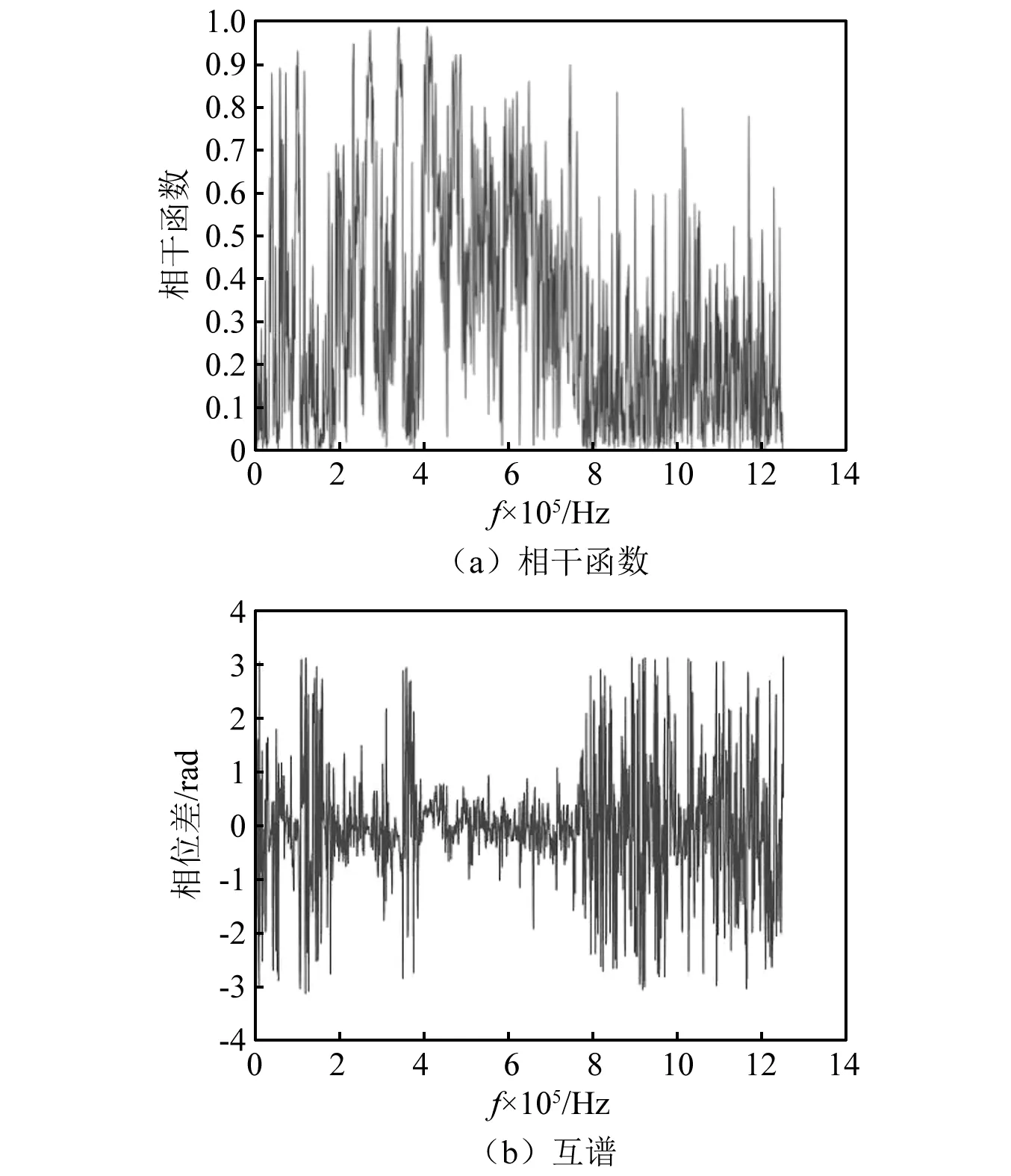
图1 s1(t)和s2(t)的相干函数及互谱相位差谱Fig.1 Coherence function and cross-spectral phase difference spectrum of s1(t) and s2(t)
由图1(a)可知,相关性较高的频段主要分布在0~500 kHz;由图1(b)可0~500 kHz内未发现明显水平差谱频段,分析其原因可能是泄漏特征信号与噪声信号相互重叠从而影响了互谱效果。为此提出一种互谱结合变分模态分解的去噪算法。
2.2 结合互谱的变分模态分解去噪算法
VMD通过迭代搜寻变分模型最优解来确定每个分量的频率中心及带宽,相比于EMD,VMD具有坚实的理论基础,有效地弥补了 EMD和EEMD等不足[13]。采集信号经过VMD后得到若干个IMF(FIM)分量和残余分量,公式如下
(8)
式中:k为VMD分解后的IMF分量个数;γ(t)为分解后的残余分量。
2.2.1 分解层数的确定
相比于EMD自适应分解信号的特点,VMD的分解层数K由人为输入,如果K过小,低频段将被划分为高频段,给模式函数的求解带来了困难。但是如果K值过大,会导致过度分解,计算时间过长。因此,分解层数的确定是VMD在应用过程中必须考虑的问题[14]。
由于采样率选用2.5 MHz,选用经验值K=10将采集信号进行VMD分解后肘频图,如图2所示。

图2 VMD分解结果时频图Fig.2 Time-frequency diagram of VMD decomposition result
由图2(b)可知,采集信号从低频到高频依次分解,并且只要分解层数选取适当可有效避免模态混叠等问题。由于高频部分的分解毫无意义,不仅消耗算力并且容易造成过度分解。因此可以通过互谱大致定位有效频段并结合滤波实现信号的去噪预处理,通过巴特沃斯滤波器滤出其中的高相似度信号,再对滤波后的信号进行VMD分解。
将信号进行互谱分析并设计低通滤波器滤出0~500 kHz的频域图,如图3所示。
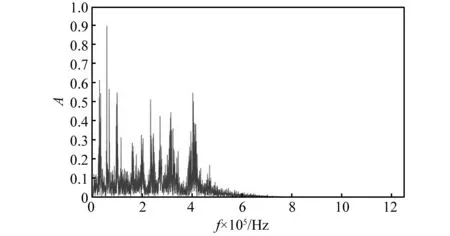
图3 滤波后频域图Fig.3 Frequency domain graph after filtering
可通过是否发生过度分解为界限确定分解层数,对滤波后的信号进行4层分解和5层分解,得出的频谱图如图4所示。

图4 VMD分解4层和5层频域图Fig.4 Result diagram of VMD decomposition layer 4 and layer 5
由图4可知,当分解至5层时第4个IMF和第5个IMF出现了过度分解现象,因此将分解层数定位4层。
2.2.2 有效模态选取
基于时差定位的管道泄漏定位试验中,主要的泄漏特征信号往往包含在VMD分解后的一个或多个模态中,因此针对有效模态的选取进行了深入研究。
目前已有的研究中,往往通过相关系数、能量值和信息熵[15]等熵值判断有效模态的选取,而以上方法都有一定的局限性。由于高频噪声的干扰,通过相关系数和能量值选取有效模态往往导致结果误差较大。而后者依据的理论是声发射作为一种动态检测方法,泄漏特征成分越多,对应信号的随机性越强,从而信息熵、样本熵等熵值较大,该方法具有一定的适用性,但是在泄漏率低的情况下仍然无法辨识出有效模态。
将采集信号经过VMD分解成10个模态后,分别计算每个模态的能量值,相关系数和信息熵结果如图5所示。
由图5可知,能量值最高的模态为IMF1,信息熵最大的模态是IMF6,相关系数最大的模态是IMF4。可见基于信息熵和相关系数选择的的IMF频段并不是泄漏特征信号所在的主要频段。为保证该试验的科学性,选取0.1 L/min(小泄漏),0.5 L/min(中泄漏),1 L/min(大泄漏)3种泄漏率下各10组试验,按经验值将信号分解至10层后,分别计算各个模态的能量值,相关系数和信息熵,记录每个模态得到最大值的次数,得到的结果如图6~图8所示

图6 0.1 L/min 泄漏率下各指标对应模态选取系数Fig.6 Modal selection coefficient of each index under 0.1 L/min leakage rate
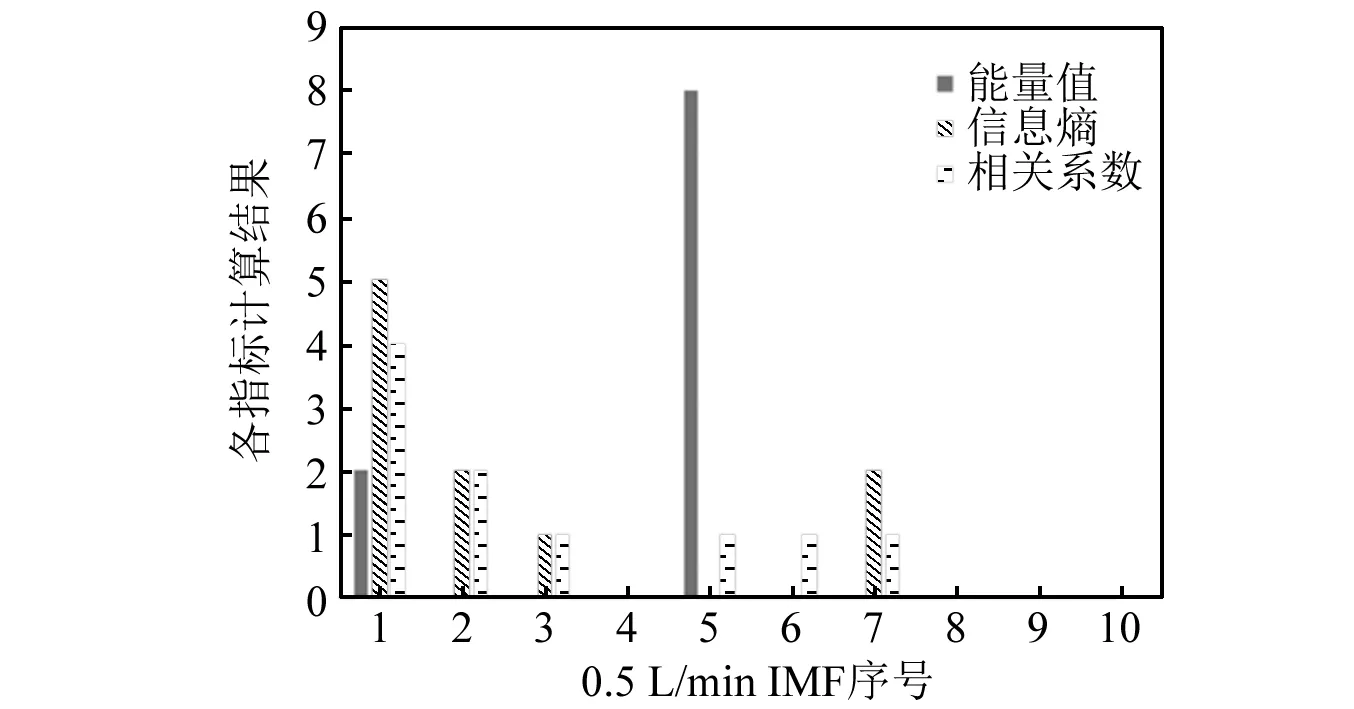
图7 0.5 L/min 泄漏率下各指标对应模态选取系数Fig.7 Modal selection coefficient of each index under 0.5 L/min leakage rate

图8 1.0 L/min 泄漏率下各指标对应模态选取次数Fig.8 Number of modal selection corresponding to each index under 1.0 L/min leakage rate
由图6~图8可知,基于单一指标的情况下容易出现高频模态被选用的情况从而导致定位结果存在较大的误差。为此提出一种结合相关系数、信息熵和能量值的综合指标,其中相关系数的选用为避免噪声的干扰采用基于互谱滤波后的信号与分解后的IMF进行互相关计算。将3个指标分别归一化后相加,取值最大的IMF为包含最多泄漏特征信号的IMF。
设能量值为a,信息熵为b,相关系数为c,将每个指标对应的数值进行归一化后再将不同指标的数值相加即得到综合指标xzonghe如下
(9)
信号经过VMD并通过综合指标选取IMF的结果分布如图9所示。

图9 不同泄漏率下综合指标选取次数Fig.9 Selection times of comprehensive indicators under different leakage rates
由图9可知,采用综合指标后选取的模态基本上集中在低频模态,结果与理论泄漏特征信号所在频段相符合,所以采用综合指标选取有效的IMF比单一指标具有更高的可靠性。
通过以上信号处理方式保证了去噪后的信号包含了尽可能多的泄漏特征信号,进而在此基础上通过FastICA算法将不同泄漏源产生的泄漏信号分离出来。
3 基于FastICA的盲源分离应用
FastICA其目标就是计算矩阵A的逆矩阵B,使其作用在观测信号x(t)上,从而可以分离解耦出具有非高斯性的接近原始信号s(t)的源信号[16],基本原理如图10所示。

图10 ICA模型Fig.10 ICA model
FastICA算法有基于峭度、基于似然最大、基于负熵最大等形式,这里采用基于负熵最大的FastICA算法,该算法以负熵最大作为一个搜寻方向,可以实现顺序地提取独立源,可以有效地将不动点迭代所带来的优良算法特性与负熵所带来的更好统计特性结合起来,使得收敛更加快速、稳健。
综合以上分析,本文提出一种互谱结合VMD的信号处理方法,并选用综合指标最大值作为选取有效IMF的依据,在管道同一侧对去噪后的信号进行盲源分离计算得到两个包含不同泄漏源特征的信号,再根据相关系数匹配出管道两侧由同一泄漏源产生的信号,最后根据时差定位得到定位结果,完整的泄漏定位方法如图11所示。
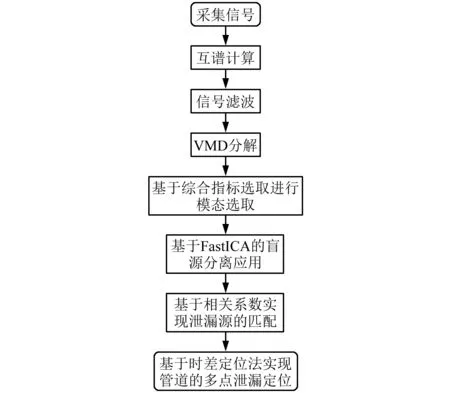
图11 多点泄漏定位算法Fig.11 Multi-point leak location algorithm
4 多点泄漏定位试验
为证明所提出方法的有效性,研究以两泄漏点为例,利用北京软岛科技公司研发的声发射采集设备对实验室搭建的管道泄漏模型展开研究,在管道上、下游分别放置两个声发射传感器,通过转动泄漏阀模拟泄漏源,设置两端传感器距离为1 300 mm,以左端传感器为基准,两泄漏源位置分别为300 mm和1 000 mm,泄漏率大小分别为1 L/min和0.5 L/min,设置管道内压为0. 3 MPa。试验方案如图12所示。
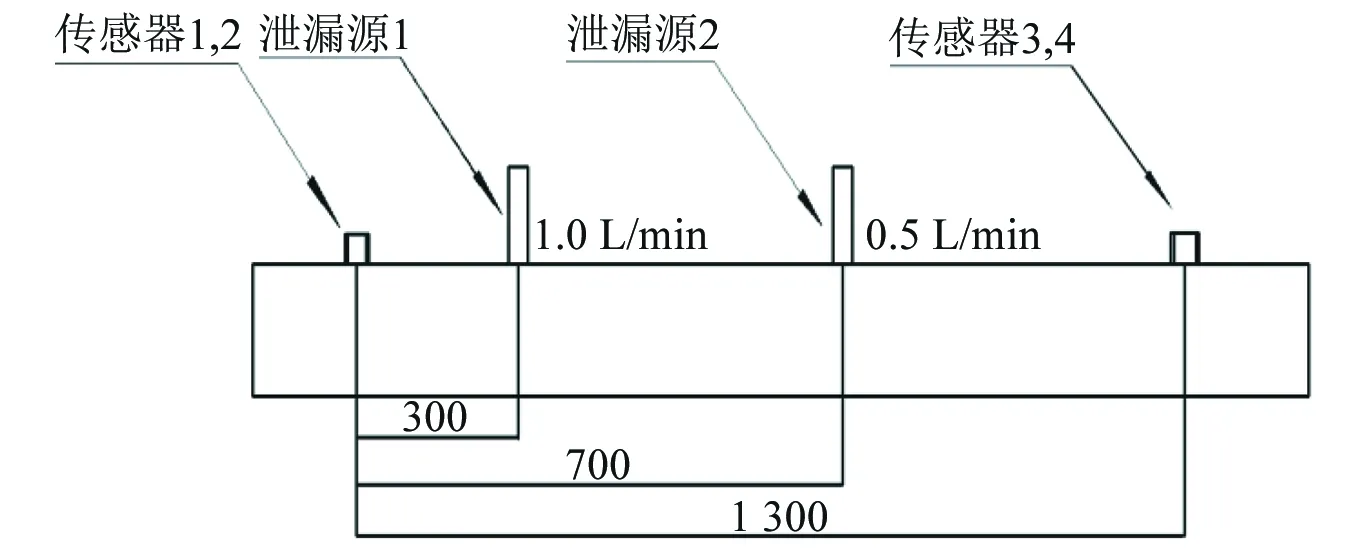
图12 多点泄漏定位试验方案(mm)Fig.12 Experimental scheme of multi-point leak location(mm)
试验装置如图13所示。

图13 管道泄漏模型Fig.13 Pipeline leakage model
以上游的两个传感器为例,两传感器采集的混合信号s1和s2频域图如下图14、图15所示。

图14 混合信号s1频域图Fig.14 Frequency domain diagram of mixed signal s1
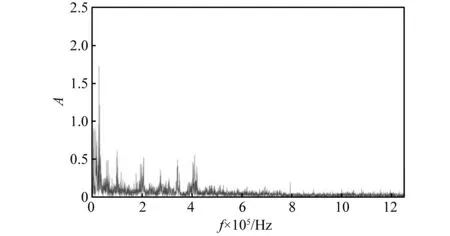
图15 混合信号s2频域图Fig.15 Frequency domain diagram of mixed signal s2
将信号进行互谱结合VMD去噪并根据综合指标选取的IMFs1和IMFs2频域图如图16、图17所示。

图16 去噪信号IMFs1频域图Fig.16 IMFs1 frequency domain diagram of denoising signal
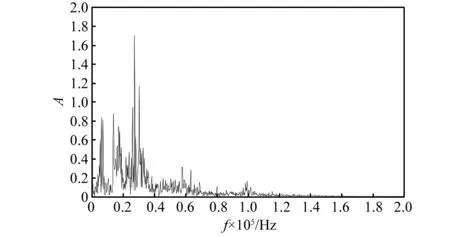
图17 去噪信号IMFs2频域图Fig.17 IMFs2 frequency domain diagram of denoising signal
对IMF1和IMF2进行FastICA计算后得到两个独立的信号源q1和q2如图18、图19所示。

图18 信号源q1频域图Fig.18 Frequency domain diagram of signal source q1

图19 信号源q2频域图Fig.19 Frequency domain diagram of signal source q2
同理计算管道下游采集的两路信号s3和s4,经过去噪处理和FastICA计算后得到信号源q3和q4,对q1,q2和q3,q4两两计算相关系数值如表1所示。

表1 信号源相关系数计算
由表1可知,(q1,q3)和(q2,q4)的相关系数较高,分别计算其相关延迟时间并得到最终的定位结果。在该工况下进行10组试验得到的试验结果如图20、图21所示。

图20 泄漏源位置为300 mm的定位结果Fig.20 Locate the leakage source at 300 mm
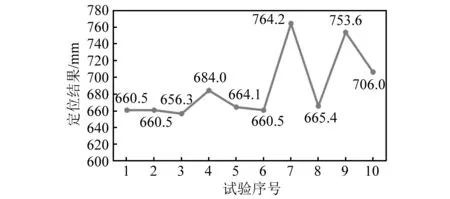
图21 泄漏源位置为700 mm的定位结果Fig.21 Locate the leakage source at 700 mm
为衡量该方法的可靠性,对试验结果进行数据分析,箱形图可以用来观察数据整体的分布情况,利用中位数,25%分位数,75%分位数,上边界,下边界等统计量来描述数据的整体分布情况。基于试验结果绘制箱型如图22、图23所示。
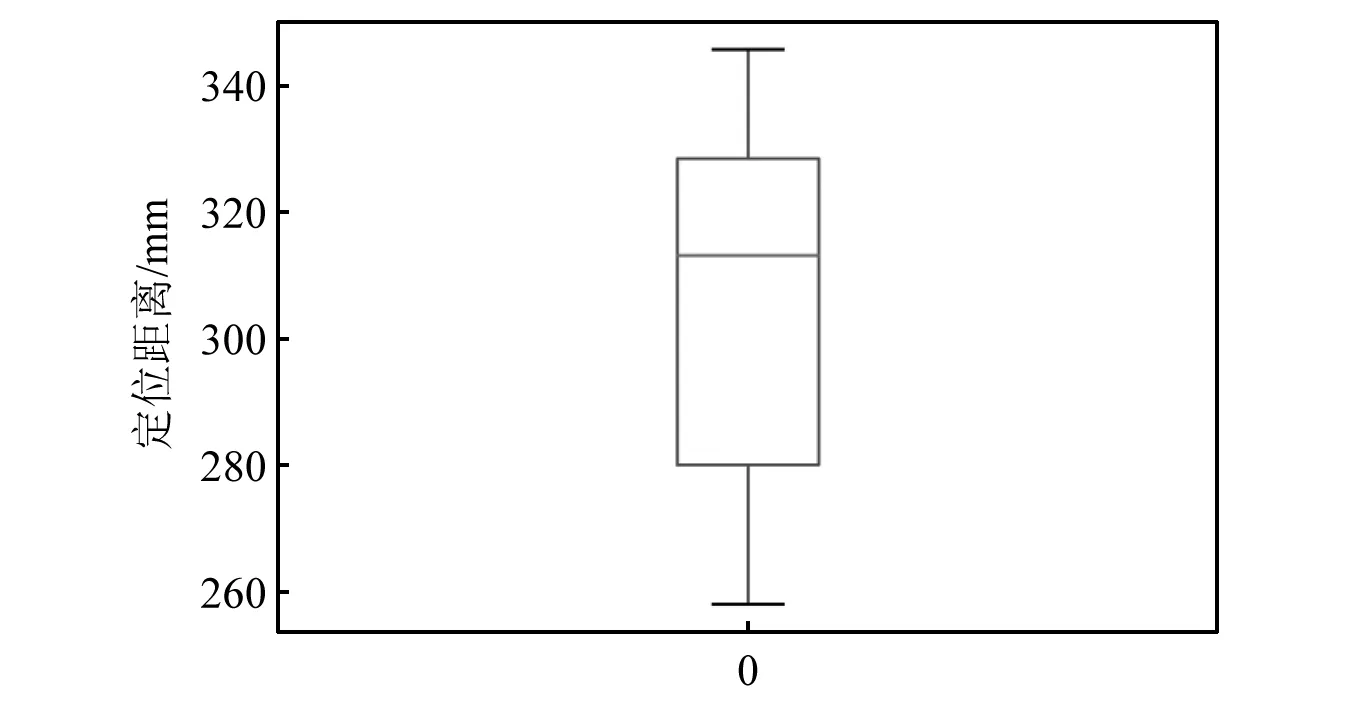
图22 泄漏源位置为300 mm的定位统计结果Fig.22 Locate the leakage source at 300 mm
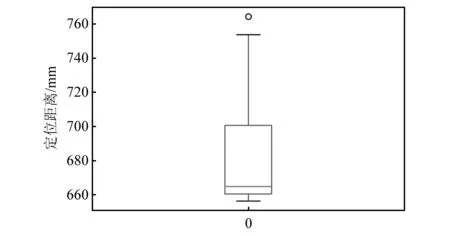
图23 泄漏源位置为700 mm的定位统计结果Fig.23 Location statistics for leak source 700 mm
由图22、图23可知,泄漏源为300 mm的定位结果较为密集得分布在300 mm左右,误差率在2%~15%,泄漏源为700 mm的定位结果存在一个偏离分布的异常值,可将其舍弃,总体误差率在1%~10%。基于以上结果分析可得,该多点泄漏定位方法具有较高的可靠性和有效性。
5 结 论
本文通过对信号进行变分模态分解后模态选取方法的研究,提出一种结合多指标的模态选取方法,并根据互谱和变分模态分解各自的局限性将两种算法结合应用,利用该算法对采集信号进行去噪预处理,将去噪后的信号通过FastICA实现源信号的分离,进而通过时差定位实现管道的多点泄漏定位。
最后,通过实验室的管道泄漏模型开展了多点泄漏定位试验,通过试验结果的分析验证了该方法的有效性,为工业实况提供了一种管道多点泄漏的理论思路。

