钢筋混凝土黏结滑移效应计算方法与应用

阮 升， 郑山锁， 张艺欣， 董立国， 王卓涵

(1.西安建筑科技大学 土木工程学院， 西安 710055； 2.西安建筑科技大学 结构工程与抗震教育部重点实验室， 西安 710055；3.华侨大学 土木工程学院， 福建 厦门 361021； 4.华南理工大学 亚热带建筑科学国家重点实验室， 广州 510640)

地震作用下，钢筋混凝土(reinforced concrete,RC)结构主要在塑性铰区域发生塑性变形[1-2]，在该过程中，构件端部锚固区的受拉钢筋通常会产生相对于混凝土的滑移，导致构件发生端部转动，从而引起构件顶端出现附加水平位移[3-8]，如图1所示。黏结滑移效应是造成地震作用下RC结构破坏的常见原因之一[9]。Sezen[10]通过RC框架柱的低周往复加载试验发现，由钢筋滑移引起的柱顶附加水平位移通常占总位移的30%以上，Murray等[11]指出当锚固条件较差时，钢筋滑移变形引起的位移甚至可达到总位移的50%，Ding等[12]通过对既有试验模拟分析也得出相似结论。Kawashima等[13-14]的研究表明柱脚处受拉钢筋的滑移会降低柱的刚度、延性和耗能能力等力学性能。Schoettler[15]等通过振动台试验指出，锚固滑移对墩顶总位移有较大贡献，能显著影响桥墩的地震反应。因此，为更加准确地模拟RC结构的地震响应，在数值分析时，钢筋与混凝土之间的黏结滑移效应不能忽略。

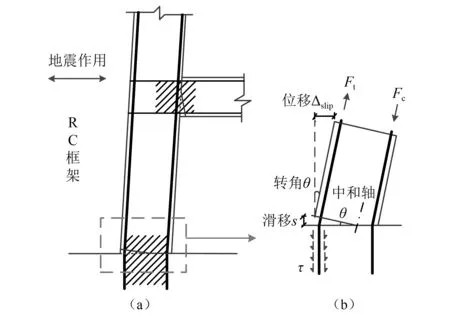
图1 构件端部钢筋滑移Fig.1 Reinforcement slip at member ends

在抗震分析中，兼顾计算效率和精度的宏观数值模型应用广泛，其可通过底部附加零长度截面单元并使用钢筋应力-滑移本构考虑钢筋黏结滑移效应。目前钢筋应力-滑移计算方法可分为细观方法与宏观方法两类[16-18]。细观方法利用黏结应力-滑移本构关系进行迭代求解获取钢筋滑移响应[19]，而宏观方法通过假设沿钢筋锚固区域的黏结应力分布函数实现对钢筋滑移的直接计算。虽然细观方法可取得较为满意的精度，但存在不足之处：需要划分一定的单元数量以保证精度，以及迭代求解黏结应力的过程需要引入大量计算等，增大了计算成本。因此，实际抗震分析中国内外学者如：Sezen等[18-23]普遍采用了假定黏结应力分布的宏观模型。但需要指出的是，现有宏观模型的假设简化了黏结应力分布，与实际黏结应力分布有较大偏差[24]，从而导致钢筋的滑移预测出现难以避免的误差。

鉴于此，为规避细观方法大量迭代以及宏观模型黏结应力分布简化造成的潜在误差，本文从物理机制出发，基于细观黏结滑移本构方程，推导了钢筋应力-滑移本构关系的理论解析模型，结合有限元模型与既有试验进行对比验证，以校准该解析模型的准确性并讨论其适用范围。

1 钢筋应力-滑移模型

钢筋局部应力与局部黏结应力平衡、局部变形与局部滑移相容是钢筋黏结滑移行为的基本关系，因此，推导钢筋应力-滑移本构模型，需选取合适的局部黏结-滑移本构模型，并建立变形相容关系进行变量代换与积分求解。

1.1 黏结-滑移本构模型

Wu等[25]考虑混凝土强度、保护层厚度、箍筋约束等因素对钢筋混凝土界面黏结应力与黏结破坏模式的影响，提出了适用于劈裂、拔出、钢筋断裂破坏的一致黏结滑移本构模型，如图2所示。该模型采用连续一致的本构方程，较好地模拟了界面黏结滑移行为。故选用该模型作为本文钢筋应力-滑移模型的推导基础。一致黏结滑移本构模型为

(1)

各模型参数计算如下

(2)

K=Kco+33Kst

(3)

Kco=c/d

(4)

Kst=Ast/(nSstd)

(5)

(6)

(7)

式中：Kco为混凝土保护层影响参数(≤3)；Kst为箍筋约束效应参数；K为混凝土保护层和箍筋的组合影响参数；fc为混凝土轴心抗压强度；c为混凝土保护层厚度；d为纵筋直径；Ast为箍筋各肢的全部截面面积；n为纵筋数量；Sst为箍筋间距；s为纵筋滑移量；τ为混凝土与钢筋在滑移s下的界面黏结应力。

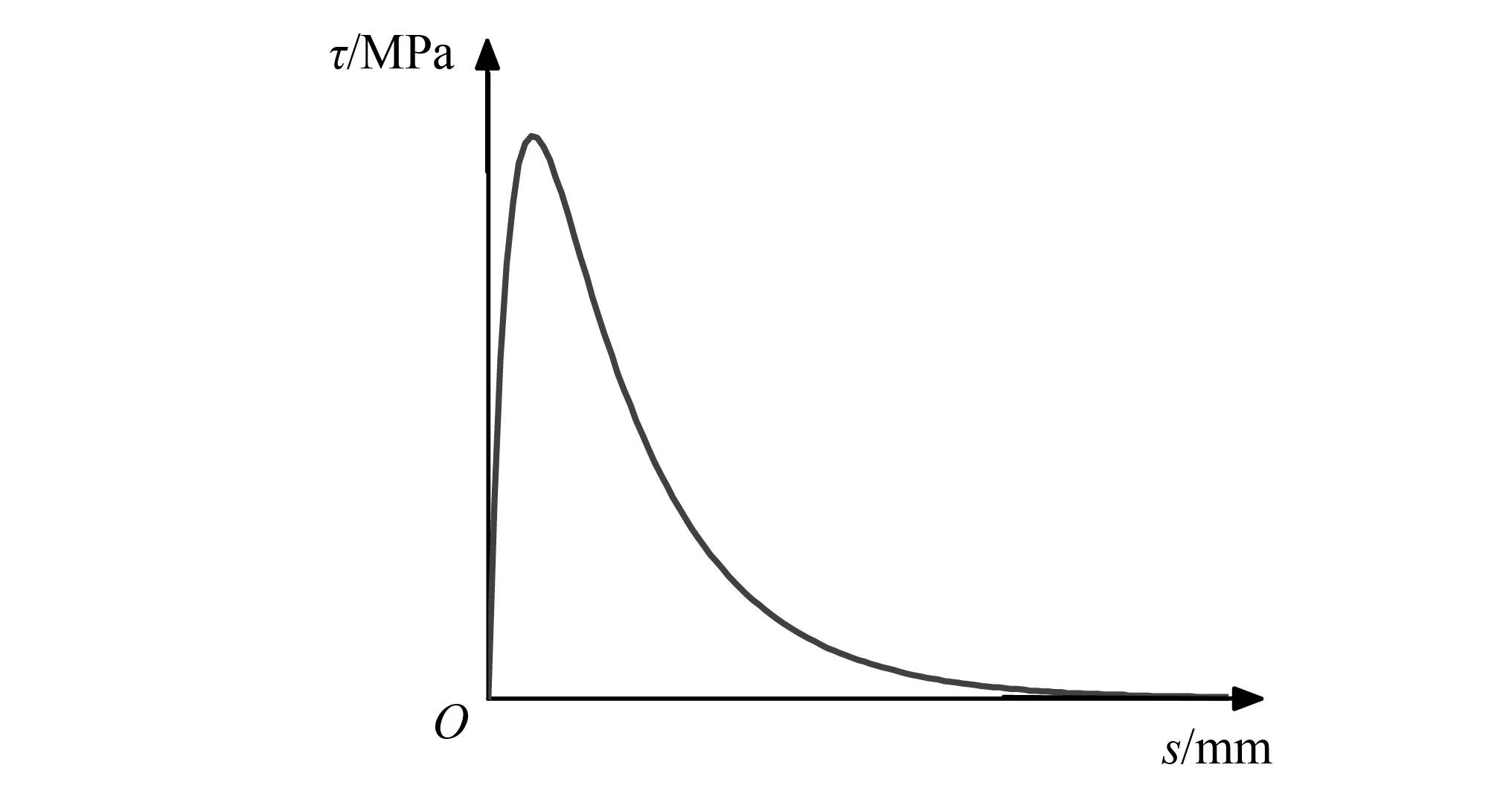
图2 一致黏结滑移模型Fig.2 Unified bond stress-slip model

1.2 钢筋应力-滑移模型推导

如图3(a)所示，在锚固区域取长度为dx的微元隔离体进行分析，其中A为钢筋截面面积，fs为钢筋应力。微元体应满足平衡方程和相容方程

(8)

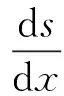
(9)

式中：d为钢筋截面直径；dfs为钢筋应力增量；ds为滑移增量；εs为钢筋应变；εc为混凝土应变，其远小于钢筋应变，故可忽略不计。

随后，将锚固长度划分成若干长度为dx的单元，由于按现行规范设计的混凝土结构，其钢筋锚固长度满足加载端发生屈服而不被拔出所需的最小锚固长度，且考虑了一定的安全系数，故在进行滑移量计算时，均认为钢筋锚固长度充分，大于黏结应力分布范围，同时，黏结应力在锚固长度内连续变化，故钢筋应力传递结束点的边界条件为

τ=0,fs=0,s=0,εs=0

(10)

将黏结应力τ=0处称为锚固点，以此为公式推导起点建立x坐标轴，如图3所示。公式中采用Menegotto[26]提出的Giuffre-Menegotto-Pinto双折线钢筋本构，故分为钢筋屈服前与屈服后两阶段分别进行推导。

1.2.1 钢筋屈服前

在弹性阶段，钢筋的本构关系为

(11)

式中，Es为钢筋的弹性模量。

对式(9)求导可得

(12)

将式(11)代入可得

(13)

将式(1)和式(8)代入式(13)，可得到关于滑移s的二阶微分方程

(14)

(15)

式中，α可根据材料和构件参数求得，在微分方程中为一常数。

进一步对式(12)进行变换，得到式(16)

(16)

εsdεs=α(eBs-eWs)ds

(17)

随后等式(17)两边同时积分，则有：

(18)

再代入式(6)及前述边界条件(s=0，fs=0)，可得式(14)的一阶解，即钢筋应力-滑移本构模型

(19)

(20)

当钢筋应力fs达到其屈服强度fy时对应的滑移量记为sy。

1.2.2 钢筋屈服后

钢筋屈服后的应力-滑移本构模型的推导方法与钢筋屈服前的相似。钢筋屈服后的本构关系为

(21)

式中，bs为钢筋硬化率。

钢筋屈服后，微元体仍然满足平衡方程和相容方程，即满足式(8)与式(9)，对式(9)求导，并代入式(21)，常数项求导为零，可得

(22)

再将式(1)、式(8)代入式(22)可得

1)MOR方案和MY方案的模拟的结果在雨带的走势上与实况十分吻合,都成功模拟出东北—西南走势的雨带,但在雨带的位置上,MOR方案模拟的效果要更接近实际情况;对于最大累积降水量的模拟,MOR方案和MY方案的最大累积降水量都超过实际情况,但相比于MOR方案,在最大累积降水量的模拟上,MY方案效果与实际更为接近。

(23)

(24)

式中，α′ 为钢筋屈服后，可根据材料与构件参数计算的一个常数。

随后，将式(16)与式(23)联立，进行变量分离后对等式两边同时积分可得

(25)

将式(21)代入式(25)，同时，由于钢筋应力-应变本构与黏结-滑移本构均为连续函数，则本文钢筋应力-滑移本构在钢筋屈服点也连续，故再根据式(19)、式(20)得到边界条件(s=sy，fs=fy)，代入式(25)可得

(26)

(27)

综上，式(19)、式(20)和式(26)、式(27)分别表征了钢筋屈服前后的应力-滑移关系，即建立了完整的钢筋应力-滑移本构模型，其计算示意如图3所示，其中钢筋锚固区域某一点的滑移量，为该点到锚固点钢筋应变的积分。图3(b)、图3(c)、图3(d)、图3(e)分别为黏结应力、钢筋应力、钢筋应变和滑移沿钢筋的分布，可通过微元平衡方程相互推导得出。

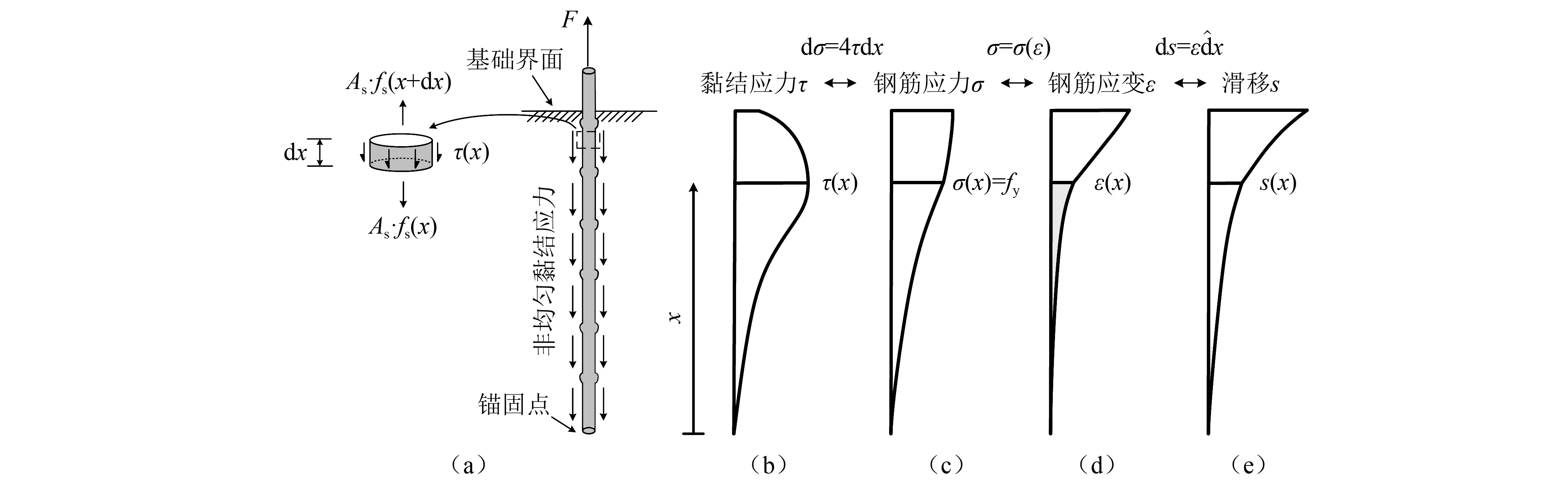
图3 钢筋滑移计算模型Fig.3 Calculation model of reinforced slip

2 模型验证及对比分析

将本文提出的钢筋应力-滑移本构模型与收集的钢筋混凝土拉拔试验数据进行对比，验证所提出本构模型的准确性和适用性。

2.1 试验概况

本文模型满足边界条件式(10)，故在此选择RC拉拔试件中钢筋锚固长度大于最小锚固长度的试验资料进行验证，以保证钢筋的自由端不发生滑移，满足模型推导条件。模型中使用的黏结滑移本构考虑了混凝土强度、保护层厚度等多个参数，为验证不同参数下本文解析模型的准确性和适用性，选择了文献[27]和文献[28]的拉拔试验试件进行计算验证，各试件主要设计参数如表1所示。

表1 拉拔构件设计参数

2.2 模型准确性验证与分析

本文模型计算的钢筋应力-滑移曲线与试验数据的对比，如图4所示。由图4可知，在弹性阶段，本文模型与试验结果吻合较好。试件SD50，S61和S107在钢筋屈服后仍然与试验结果有较高的吻合精度，但对于试件B103和S64，在非弹性阶段初期，本文模型预计的滑移量略小于试验值，这可能是由于试验中钢筋屈服强度的离散性导致，故在模型中输入的钢筋屈服强度无法完全与试验中钢筋的屈服强度相同，从而造成本文模型的转折点滞后于试验，造成滑移预计值偏小。在非弹性阶段后期，本文模型与试验结果亦可较好地吻合。总体而言，本文模型能较客观地反映钢筋在弹性与非弹性阶段的滑移行为。

图4 拉拔试验结果与本文模型对比Fig.4 Comparison of pull-out test results and proposed model

3 数值模拟应用

纤维模型可较好地模拟RC受弯构件的受力性能，但该模型的几何关系遵循了严格的平截面假定，因而无法准确模拟钢筋的黏结滑移效应。为改善这一不足，Zhao等[16]提出在构件端部附加一个零长度纤维截面单元，采用与上部纤维梁柱单元相同的截面划分形式，并将其中的钢筋本构关系替换为钢筋应力-滑移本构，将钢筋的黏结滑移效应以端部附加转角的形式叠加到构件变形中。根据该思路，本文基于OpenSEES[29]平台，通过在端部附加零长度截面单元，将本文所提出的钢筋应力-滑移解析模型嵌套其中，建立零长度纤维模型(本文模型)对已有试验进行模拟对比，同时，将零长度纤维模型中零长度截面单元所嵌套的钢筋应力-滑移解析本构，替换为基于Sezen等的研究中平均黏结应力分布假设得到的钢筋应力-滑移本构，建立数值模型(既有模型)，与本文模型进行对比，以验证本文模型在RC构件层面的准确性。

3.1 数值建模方法

采用OpenSEES中基于刚度法的非线性纤维梁柱单元dispBeamColumn与零长度截面单元zeroLengthSection串联，建立考虑黏结滑移效应的数值模型，其中，非线性梁柱单元选用3个积分点计算。保护层混凝土的本构关系采用Concrete 01单轴混凝土本构[30]，即不考虑保护层混凝土抗拉强度；核心区混凝土采用Mander模型[31]计算箍筋对混凝土的增强效应，对混凝土强度和应变进行修正，并采用Concrete 04材料进行模拟。梁柱单元中钢筋本构关系采用可以考虑钢筋各向同性应变硬化和包辛格效应的Steel 02材料模拟。

零长度截面单元中的钢筋本构采用Hysteretic材料模拟，其骨架参数根据本文及Sezen等的研究提出的钢筋应力-滑移本构关系计算标定，其滞回规则控制参数参见Zhao等的研究。模型示意如图5所示。

图5 零长度纤维模型Fig.5 Zero-length fiber model

3.2 试验验证

本文选择缩尺程度较小、截面尺寸大、以弯曲破坏为主的构件试验进行验证。文献[13-14] 和文献[32-33]分别对钢筋混凝土框架柱和桥墩构件进行了拟静力加载试验，在模拟文献[33]试验时，取模型悬臂计算高度为1 473 mm，即框架柱构件反弯点至基础的距离，模拟文献[13]、文献[14]和文献[32]的试验时，取构件水平荷载加载点至基础的距离为模型悬臂计算高度，分别取为1 350 mm，2 440 mm，1 000 mm。构件设计参数如表2所示，构件高度、截面尺寸和配筋形式，如图6所示。

表2 试验框架柱和桥墩设计参数

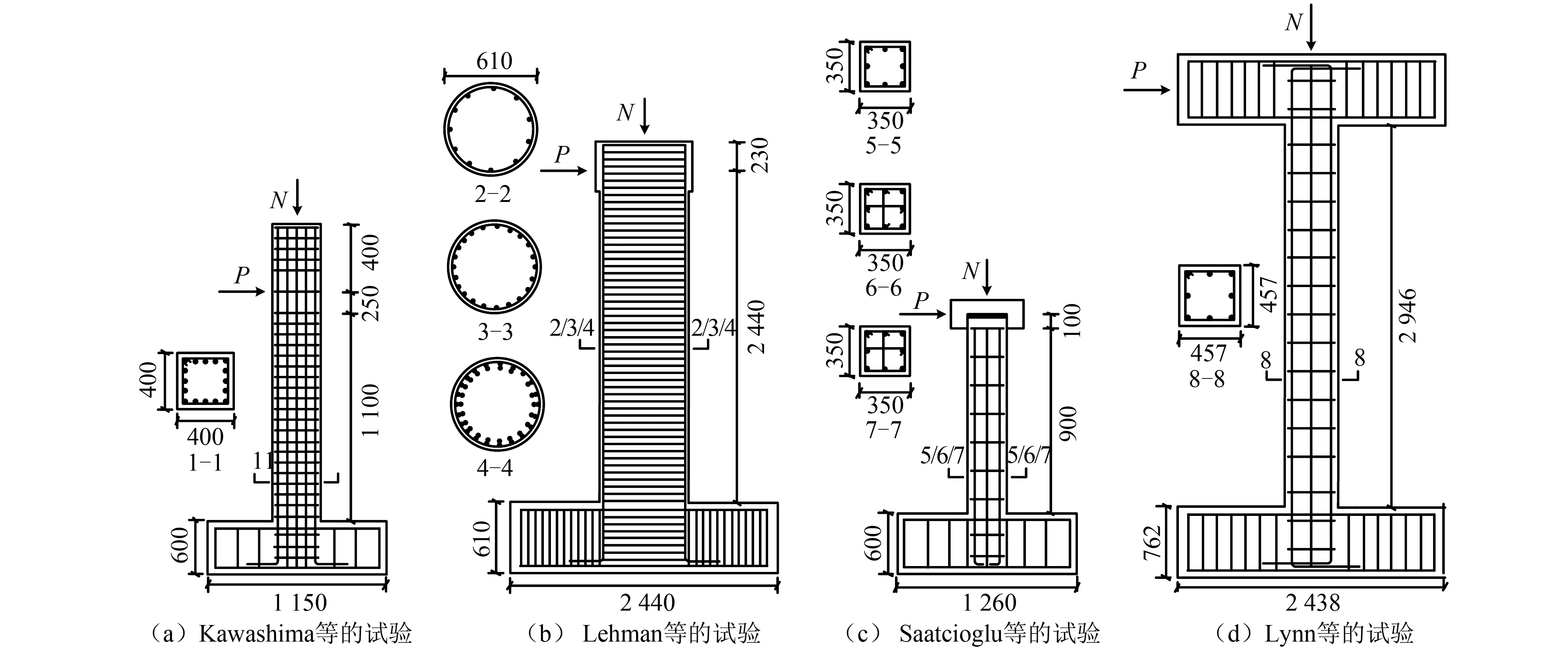
图6 试验框架柱和桥墩构造(mm)Fig.6 Details of test frame column and bridge column (mm)

3.3 荷载-位移反应

所选取的8个试件滞回曲线的试验结果与不同模型计算结果的对比，如图7所示。从图7可以看出，与既有模型相比，本文模型计算滞回曲线与试验滞回曲线吻合较好。本文模型在初始循环加载时，各试件的承载力、初始刚度与变形的计算结果与试验结果吻合度较高；在多次循环加载后，部分试件承载力出现一定程度的偏差，但总体强度退化趋势与程度仍与试验结果接近，各试件的卸载刚度和刚度退化与试验结果均较为相符，本文所建立纤维模型中，增加了零长度截面单元，可以在一定程度上反应由于钢筋滑移导致的捏缩效应[34-35]，故模拟滞回曲线均出现一定程度的捏缩，而试验滞回曲线相对于模拟结果，出现不同程度的较大捏缩，这可能是由于试验中的剪切变形影响了构件的耗能能力。对比图7(a)、图7(b)、图7(c)可以看出，相比于试件U4，试件U6和U7的模拟滞回曲线捏缩效应与试验滞回曲线捏缩效应的误差更小，这是由于试件U6和U7的配箍率大于U4，从而剪切承载力退化更小，剪切变形减小，捏缩效应误差减小，这说明剪切变形的确是导致模型与试验产生一定误差的原因。

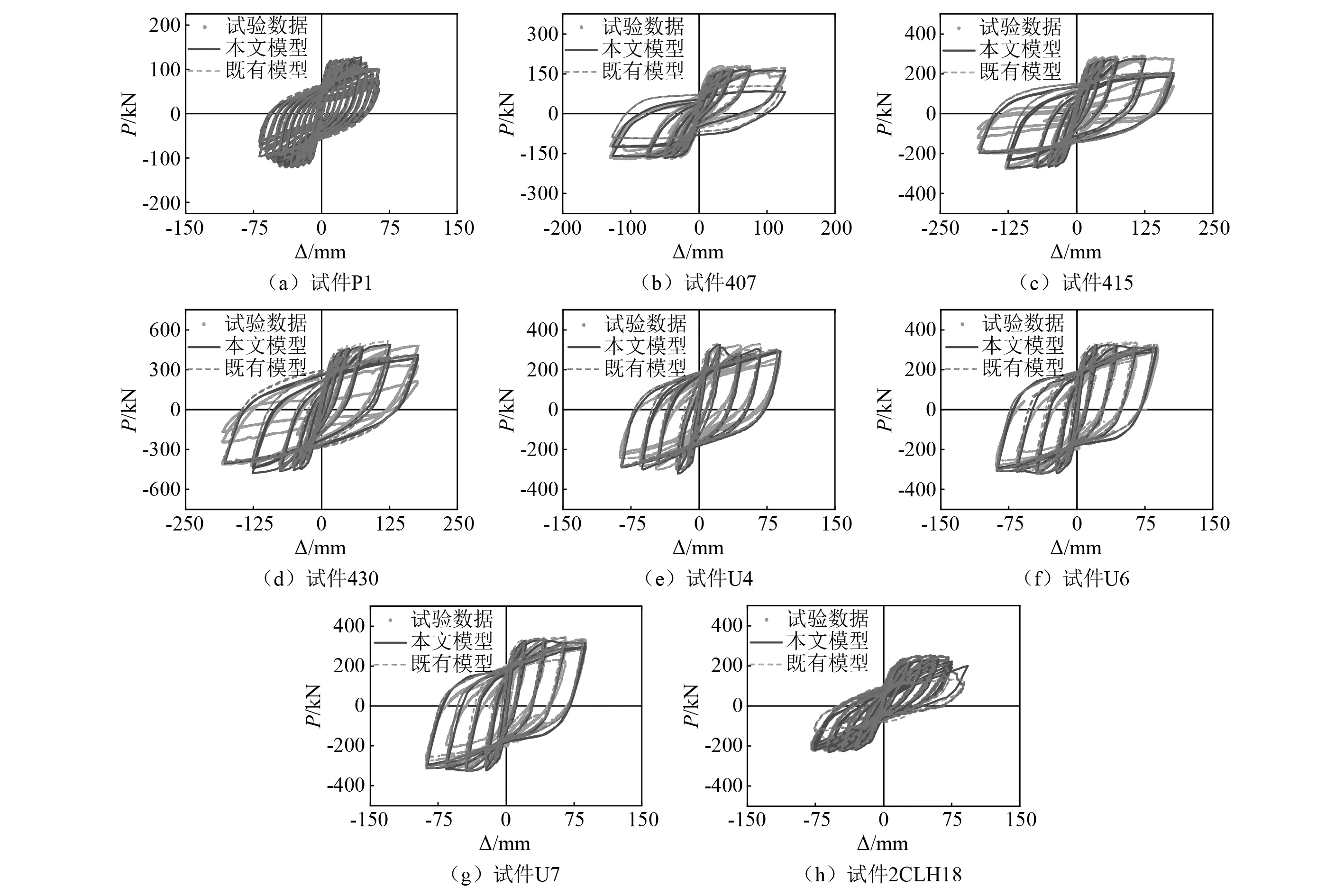
图7 模拟结果与试验结果对比Fig.7 Comparison of simulation and test results

而从图7可以看出，既有模型计算所得结果存在初始刚度偏大、强度退化过早的问题，这是由于既有模型对于钢筋的黏结滑移效应估计不足，使得在相同位移下，钢筋滑移产生的柱顶附加位移较小，进而模型梁柱单元中混凝土纤维需产生更大的弯曲变形以满足位移需求，造成试件的初始刚度偏大，同时，在后续加载中，导致更多的混凝土纤维单元破坏失效，试件强度退化提前。

基于上述不同模型计算结果及与试验结果的对比分析，总体而言，基于本文提出的钢筋应力-滑移本构，结合零长度截面单元建立的有限元模型，可较好地模拟以弯曲破坏为主的RC构件的变形、承载力和滞回过程。

3.4 柱顶附加水平位移

钢筋滑移导致构件端部出现附加转角，从而使构件顶端产生附加水平位移(Δslip)。本文通过在有限元模型中提取零长度截面单元中钢筋纤维的应力-滑移关系和梁柱单元中钢筋与混凝土纤维的应力-应变关系，根据式(28)计算柱顶附加水平位移

(28)

式中：h为截面高度；hc为柱的受压区高度。

图8所示为不同纵筋配筋率试件407，415，430加载过程中，由钢筋滑移产生的柱顶附加水平位移在柱顶总水平位移中的占比。对比本文模型、既有模型与试验结果可以看出，本文模型计算结果与试验数据误差较小，相比于既有模型更为接近试验，而既有模型低估了钢筋的滑移量，造成柱顶附加水平位移偏小，且既有模型难以反映构件纵筋数量变化产生的影响，随着构件纵筋数量的增加，模型对钢筋黏结滑移效应的低估愈发明显，这也与滞回曲线中分析结果相一致。

通过上述不同模型计算结果与试验结果的比较，可以看出，基于本文提出的钢筋应力-滑移本构建立的零长度纤维模型，较好表征了整个加载过程中钢筋的黏结滑移行为，证明了本文提出的钢筋应力-滑移本构能很好的与零长度截面单元嵌套，具有较强的适用性。此外，从滑移占比结果也可看出，在构件受力过程中，滑移占比较大，在模拟分析中不能忽略。

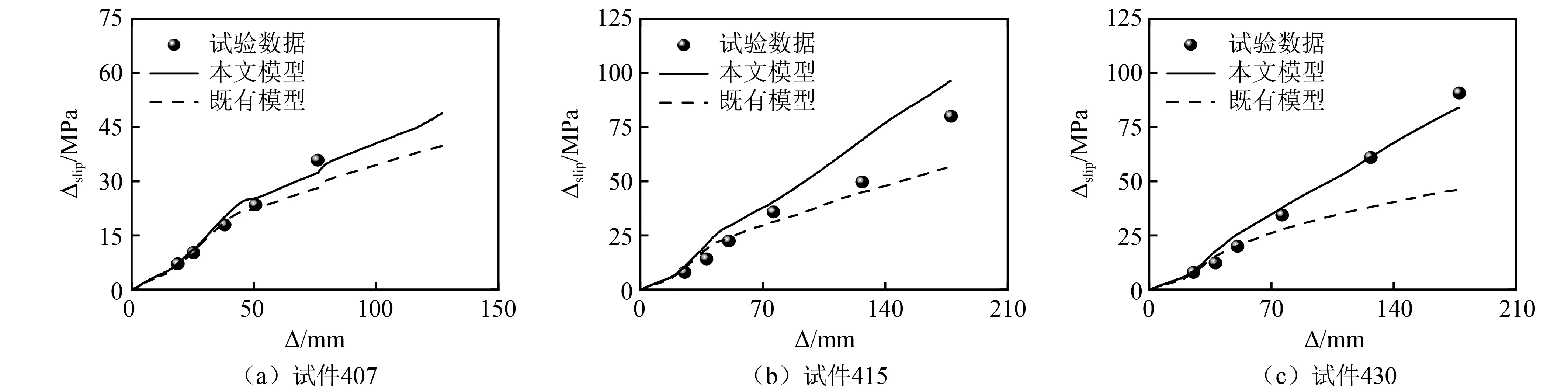
图8 柱顶附加水平位移占比结果与试验数据的比较Fig.8 Comparison of proportion results of column additional displacement and test data

4 结 论

(1)本文基于一致黏结滑移本构模型，通过微元方程求导后再积分的方法，避免了宏观模型假设黏结力分布产生的误差和细观模型的迭代计算，推导出可直接应用于有限元计算的钢筋应力-滑移理论解析模型。

(2)通过与钢筋拉拔试验对比分析，验证了本文所提出的钢筋应力-滑移模型能较好地反映长锚固钢筋受拉时的滑移行为。

(3)采用本文提出的钢筋应力-滑移模型，模拟得到的滞回曲线与试验滞回曲线吻合良好，能合理的表征RC构件的承载力、刚度及其退化程度，客观地反映了以弯曲破坏为主的RC构件抗震性能，而既有模型对于其刚度与强度退化的预测结果不够理想。

(4)本文提出的钢筋应力-滑移模型能客观地反映钢筋混凝土黏结滑移效应在构件整个受力过程中的变化，而既有模型难以准确捕捉构件加载过程中的钢筋滑移行为。