变摩擦自复位支撑钢框架的抗震性能影响因素研究

王永玮， 周 臻， 赵坤松

(东南大学 混凝土及预应力混凝土结构教育部重点实验室，南京 210096)

传统抗弯框架(moment-resisting frame, MRF)通常通过梁柱节点的塑性变形耗散地震能量，因此在地震作用后，结构通常会产生不可修复的残余变形，增加维修费用。作为下一代基于性能设计的核心思想，未来抗震设计的重点从“抗倒塌设计”转为“可恢复设计”[1]。

自复位耗能(self-centering energy dissipation, SCED)支撑由于不需要改变原有结构体系、破坏梁柱节点的完整性，已得到学者的广泛关注。SCED通常由提供恢复力的自复位系统和提供耗能的阻尼器组成，通过两者的有效连接，形成稳定的旗帜形滞回特性[2-3]。Zhou等[4-5]通过对多种自复位支撑的试验，验证了双套管自复位支撑良好的工作性能。然而自复位支撑框架由于屈服后刚度较低，在大震下通常表现为顶层加速度、位移角过大等现象，对结构震后可修复提出了挑战[6-8]。

为控制结构高阶模态带来的不利影响，Qiu等[9]研究得出支撑屈服后刚度及耗能能力的提升均有效缓解框架结构的高阶模态效应。尽管增加结构抗侧刚度，如重力框架[10]、填充墙[11]等均可有效改善结构沿层高分布的位移角，但结构形式的改变将增加施工过程的难度和费用，难以在实际生活中推广应用。

变摩擦、变刚度阻尼器可根据变形大小自动改变自身的摩擦力或刚度，以提供更大的耗能需求。相比Xu等[12]提出的磁流变自复位支撑，基于坡面摩擦板构造设计的被动式变摩擦耗能器，具有构造简便、性能稳定等优点，得到了广泛应用[13]。因此，Hashemi等[14-15]提出了一种无需传统预应力筋的变摩擦阻尼器。摩擦材料通过坡面摩擦板及弹簧，提供自复位恢复力。但该类型阻尼器由于缺少自复位系统的初始预拉力，使其启动荷载较低，小震下即产生变形与我国抗震规范不符。

本文结合基于坡面摩擦板设计的变摩擦耗能器(variable friction damper, VFD)[16]及玄武岩纤维筋(basalt fiber-reinforced polymer, BFRP)，提出了一种变摩擦自复位支撑(variable friction damper-self-centering brace, VFD-SCB)。首先介绍了VFD-SCB的工作机理和力学性能，然后基于OpenSees对滞回模型进行二次开发，并将计算结果与理论模型和试验结果进行对比。在此基础上建立了传统抗弯框架与VFD-SCB框架，研究了支撑关键参数对钢框架抗震性能的影响。

1 VFD-SCB力学分析

1.1 工作机理

VFD-SCB主要由提供恢复力的预应力BFRP筋及耗散地震能量的VFD组成，如图1所示。

图1 VFD-SCB基本构造Fig.1 The concept of VFD-SCB

无论支撑受拉或受压，内、外套管及端板组成的自复位体系使BFRP始终处于伸长状态，为支撑提供稳定的自复位恢复力；变摩擦耗能体系通过多组碟簧提供正压力，两块Q345坡面板、不锈钢与非石棉有机摩擦材料(non-asbestos organic, NAO)两个滑动面提供摩擦力，有效耗散地震能量。通过设置连续高低起伏的平面和坡面，阻尼器分为平面滑动段(Lf)及坡面滑动段(Ls)。当支撑变形超过平面滑动段长度时，阻尼器进入坡面滑动段，两坡面板产生间隙，外坡面板压缩碟簧，增大摩擦面的法向正压力及摩擦力。相比支撑在平面滑动段，支撑在坡面滑动段将提供更大的摩擦力及刚度，这种现象称为“变摩擦”。

1.2 平面滑动段

与传统摩擦耗能型自复位支撑相似，VFD-SCB支撑在平面滑动段的正压力及摩擦力恒定，因此自复位体系的启动力Fa与启动位移La，可以表示为

Fa=Fp+Fμ=Fp+2nP(μg+μn)

(1)

La=Fa/ksc

(2)

式中：Fμ为VFD在平面段的摩擦力；Fp为自复位体系的初始预应力；n为螺栓数量；P为碟簧初始预压力；μg与μn分别为钢板与钢板、不锈钢板与NAO接触面的滑动摩擦因数；ksc为自复位体系的第一刚度。

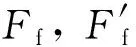
Ff=Fa+kbf(Δ-La)

(3)

(4)

式中，kbf为BFRP的刚度。因此，在平面滑动阶段，与传统自复位支撑相同，VFD-SCB的刚度仅由自复位体系，即BFRP提供。

1.3 坡面滑动段

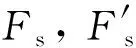
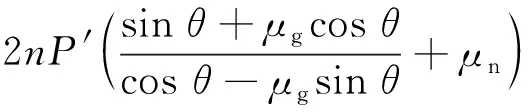
(5)

(6)

式中：θ为VFD坡面角度；P′为VFD上坡以后碟簧提供的正压力，可以表示为

P′=P+kdtanθ(Δ-Lf)

(7)

式中，kd为VFD中碟簧组刚度。

因此，在VFD上坡以后，支撑刚度由VFD构造参数及BFRP共同提供，大于平面摩擦段支撑刚度及摩擦力，表现为“变摩擦”现象。

在理想状态下，内外套管长度应完全相同(见图1)，但考虑到实际存在的加工及装配误差，内外套管的长度差异使支撑变形时无法完全协同工作，因此支撑的第一刚度小于理论值，参考Xie等[17]提出考虑套管长度误差的第一刚度修正系数ρSC1

(8)

式中：ΔL为套管长度误差；kin及kout分别为支撑内、外套管刚度。假设当内外套管长度误差为1 mm时，第一刚度修正系数为0.028。

基于式(1)～式(8)，确定VFD-SCB的新型变刚度滞回曲线，如图2所示。

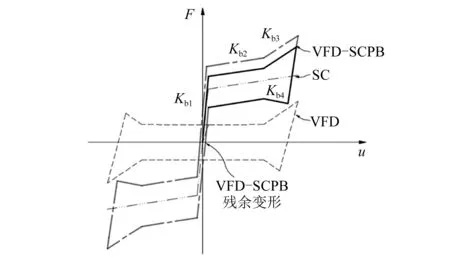
图2 VFD-SCB理论滞回曲线Fig.2 The hysteretic curve of VFD-SCB

2 支撑滞回模型二次开发

由于VFD-SCB的特殊构造机理和滞回曲线与传统SCED存在较大区别，因此根据VFD-SCB位移及轴力的计算公式，借助开源有限元软件 OpenSees及编程语言C++，对VFD-SCB滞回模型进行二次开发。计算考虑第一刚度修正系数的理论分析及有限元模型，并与文献[18]的试验结果对比如图3所示。

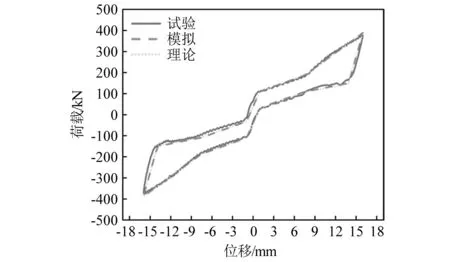
图3 VFD-SCB滞回曲线对比Fig.3 The comparison between test and simulation results

由图3可知，在考虑第一刚度修正后，理论模型、有限元分析结果与试验结果表现出较好的一致性。在达到坡面启动位移后，VFD-SCB均表现出“二次启动”及“变刚度”，呈现明显的新型旗帜型滞回曲线。同时支撑残余位移较小，说明支撑在实现两阶段三刚度后，仍表现处良好的自复位性能。因此，本文开发的VFD-SCB滞回模型在OpenSees中能有效模拟支撑的滞回特性。

3 支撑框架有限元建模

3.1 钢框架基本信息

基于Tremblay等的研究中8层铰接支撑钢框架，建立对应的OpenSees有限元模型，并将文献中SCED支撑框架替换为VFD-SCB支撑。由于结构平面布置较为规则，在忽略结构的扭转后，将模型简化为二维框架进行建模，自复位支撑框架结构布置如图4所示。其中支撑为结构唯一的抗侧力构件，代表y方向框架最外侧的两榀支撑框架(见图4(a))。其余部分为重力式框架，仅承受结构的重力荷载不提供抗侧刚度。因此，将三榀框架等效为重力柱，采用上下铰接的方式用于模拟重力式框架的P-Δ效应。

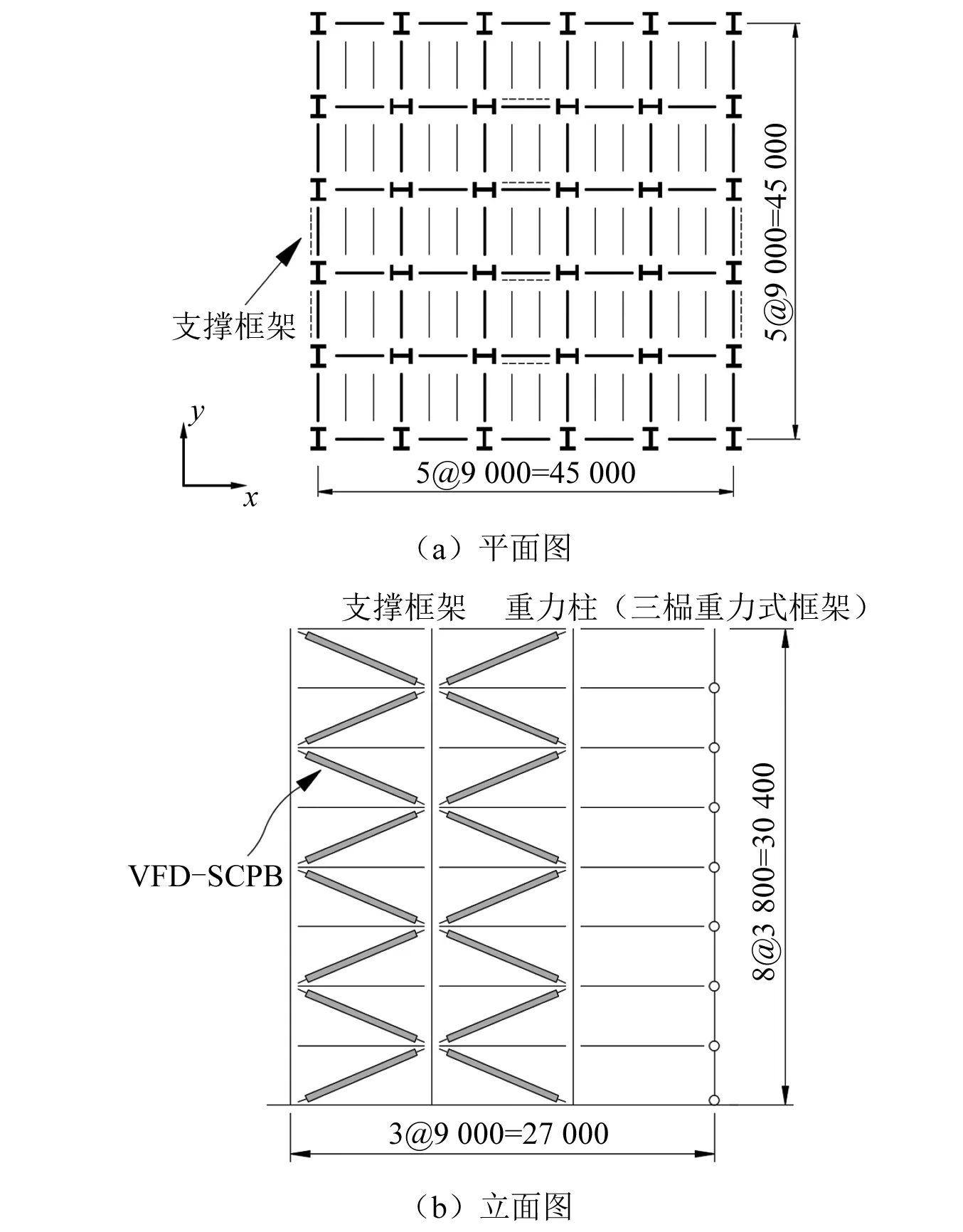
图4 自复位支撑框架结构布置图Fig.4 The schematic of braced frame

基于ASCE 7-10等效静力法确定VFD-SCB框架的设计地震荷载及各楼层的水平地震力后，计算得到各楼层支撑的设计轴力和启动荷载。为保证地震作用下框架沿层高具有较均匀位移角，满足结构在设防地震水平(design based earthquake, DBE)和罕遇地震水平(maximum considered earthquake, MCE)的抗震目标，由于在小震和中震下，传统的平面自复位支撑已经可以满足结构抗震需求，可以同时控制结构峰值位移角及减小结构残余变形。然而，大震下由于自复位支撑较低的耗能能力，使结构峰值位移角增大，影响结构的可恢复性能。因此，为避免小震和中震下支撑轴力给梁柱节点带来过大的荷载，VFD-SCB设计为在2.0%位移角内处于平面滑动段，大于2.0%后支撑进入坡面滑动段。VFD-SCB框架的重要设计参数如表1所示。

表1 VFD-SCB框架参数Tab.1 The parameters of VFD-SCB frame

3.2 地震波选取

参考Somerville[19]的研究，考虑地震动频谱特性、强度和持时的差异后，选取40条地震波，分为DBE(LA01-LA20)和MCE(LA21-LA40)，并在每条地震波后增加40 s的零加速度，计算结构的残余位移。地震波的反应谱，如图5所示。

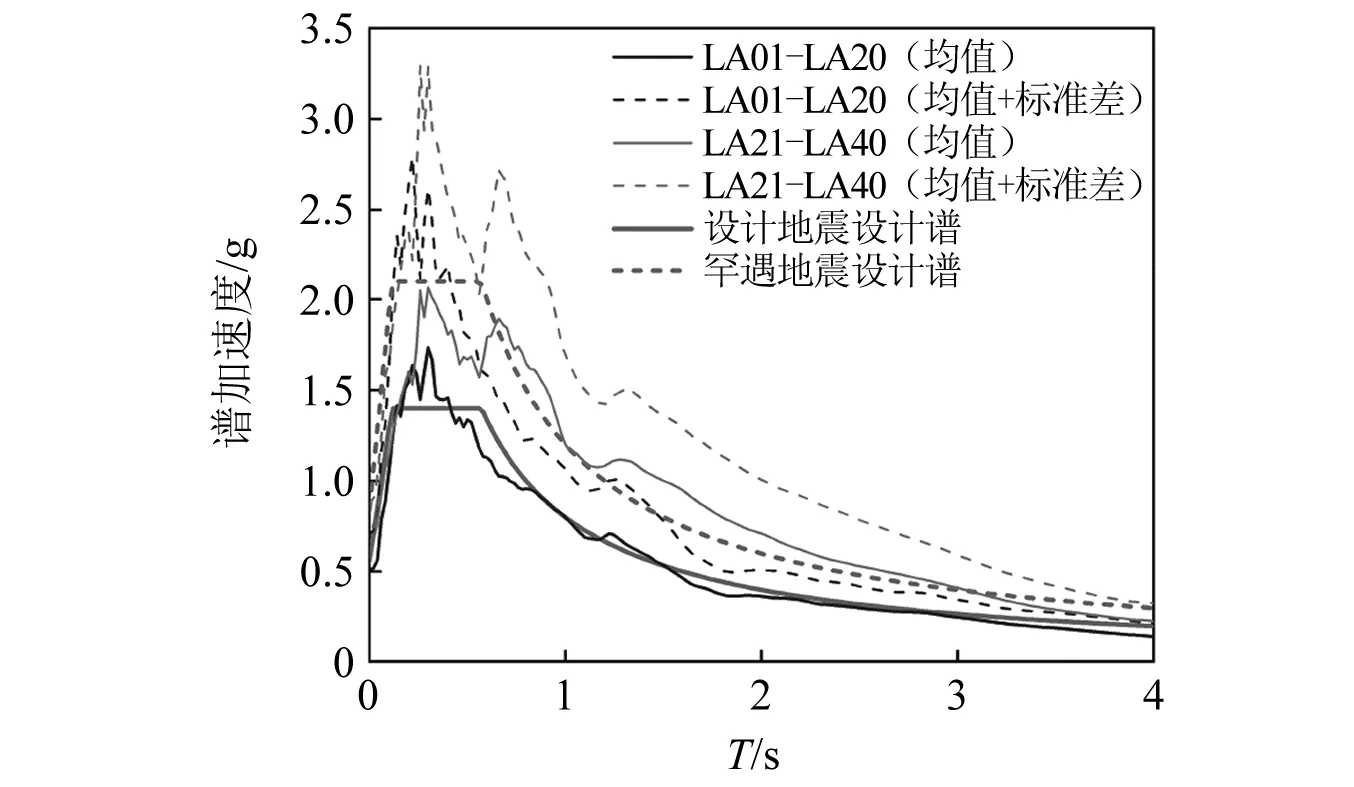
图5 地震动反应谱及设计谱Fig.5 Elastic response spectra of ground motions

3.3 VFD-SCB工作性能

为验证VFD-SCB在框架中的工作性能，分别提取最大层间位移角为1.92%的LA16地震波作用下的DBE，最大层间位移角为3.04%的LA28地震波作用下的MCE及最大层间位移角为4.71%的LA36地震波作用下的DBE支撑变形及轴力的计算结果，如图6所示。

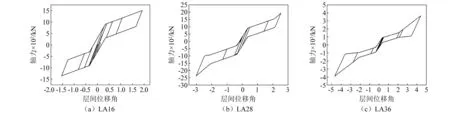
图6 不同地震波下VFB-SCB滞回曲线Fig.6 Hysteretic responses of VFD-SCB under different ground motions

在LA16作用下，支撑位移角未超过2%的限制，说明支撑及变摩擦阻尼器仅在平面段滑动，未进入上坡段(见图6(a))。此时支撑滞回曲线与传统SCED相似，表现出传统的旗帜形滞回及恒定的启动后刚度。同时支撑满足设计要求，在DBE作用下未进入坡面滑动段，在有效减小结构的残余位移、提高结构可恢复性能的同时，并未给梁柱节点带来过大的荷载。

在LA28及LA36的作用下，支撑位移角大于2%限值。此时，支撑及VFD进入坡面滑动段，坡面摩擦段压缩碟簧，碟簧提供更大的正压力，因此支撑摩擦力增大(见图6(b)和图6(c))。同时可以看出支撑表现出明显的二次启动和第三刚度，滞回曲线更加饱满，因此可以耗散更多地震能量。由于受加工误差的影响，VFD-SCB在考虑支撑第一刚度修正系数ρSC1后，表现出一定的残余位移，但残余位移角小于0.2%，未影响其自复位性能。因此，本文开发的DSC-VFD可以有效模拟支撑在地震下的工作性能。

4 框架抗震性能参数化分析

4.1 VFD-SCB地震响应

建立具有相同地震力及基本周期的抗弯框架，计算结构地震响应并与VFD-SCB框架对比，如图7所示。结果中，50th为结构响应平均值，表示其超越概率为50%；84th为结构的平均值与标准差之和，表示其超越概率为16%，用来评价地震响应的离散性。

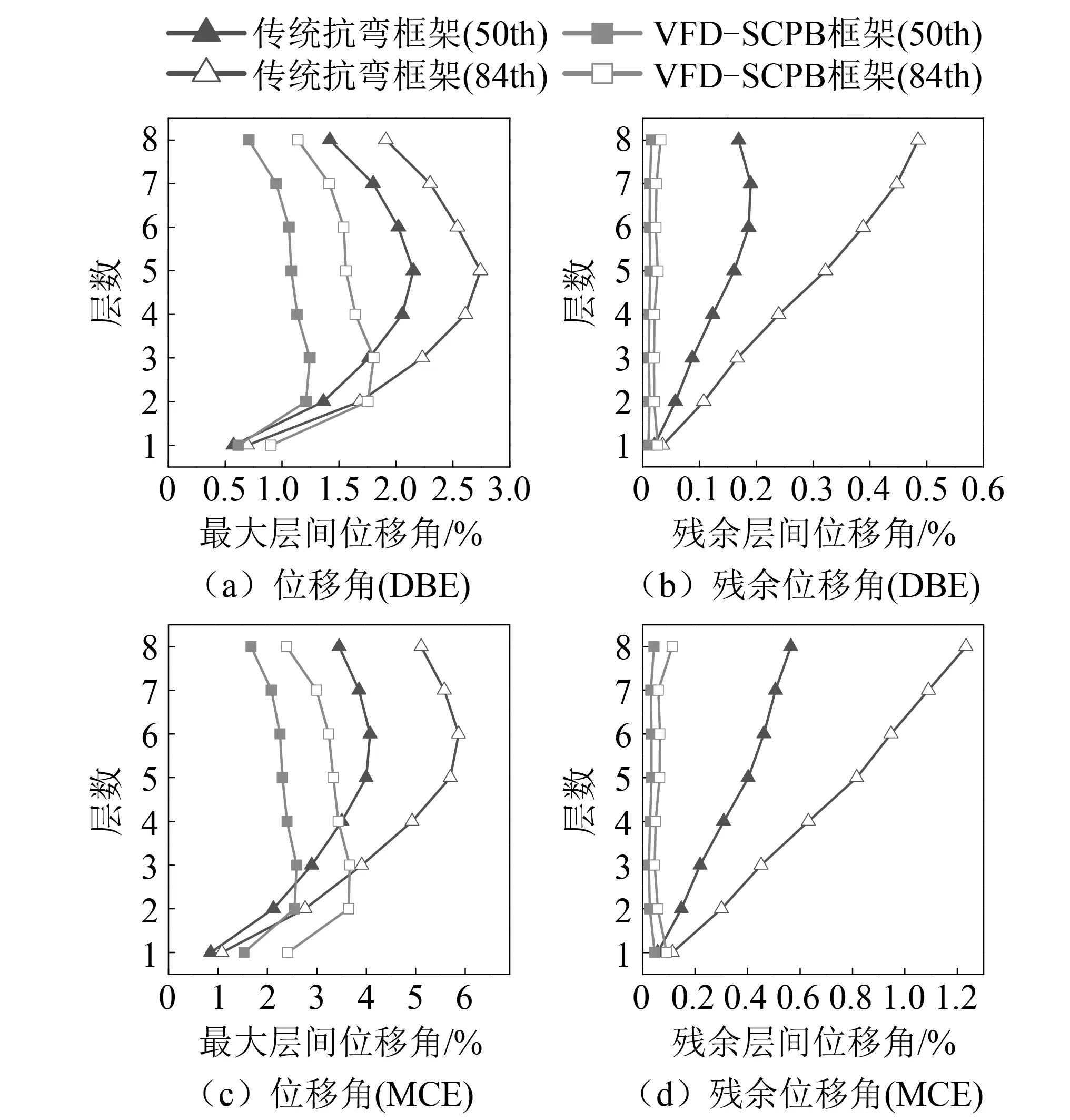
图7 抗弯框架与VFD-SCB框架Fig.7 Seismic responses of traditional MRF and VFD-SCB frame

在DBE及MCE作用下，与传统抗弯钢框架结构最大层间位移角出现在中部不同，VFD-SCB框架的最大位移角出现在结构底部，同时位移角沿层高分布更加均匀。VFD-SCB框架在DBE下最大位移角小于2.0%，在MCE下最大位移角小于3.0%，说明VFD-SCB框架各楼层的位移角均得到有效改善，表现出良好的抗震性能。

在地震作用后，VFD-SCB框架的残余位移角小于0.1%，表现出良好的自复位性能。而传统抗弯钢框架的残余位移角沿层高呈现增长趋势，在MCE下，传统框架的最大残余位移角已经达到0.56%，超过重建费用的位移角限值0.5%。因此VFD-SCB不仅减小结构的最大变形，同时能有效控制结构残余位移，提高结构震后可修复能力，满足韧性城市的需求。

为探索VFD-SCB在地震作用下关键参数的合理取值范围，基于上述VFD-SCB框架为基准模型(fundamental benchmark, FB)，研究关键参数对框架抗震性能的影响。由于采用VFD-SCB支撑均有效减小了结构残余位移，因此仅对框架的最大位移角进行研究。

4.2 支撑第一刚度的影响

在设计时VFD-SCB框架的第一刚度与传统框架应保持一致，但由于制造误差等因素影响往往难以达到设计第一刚度。因此，相对于FB，控制VFD-SCB框架中支撑的第一刚度(K1)分别为FB的0.7倍和1.3倍，记作FB-0.7K1，FB-1.3K1，计算支撑第一刚度对框架抗震性能的影响如图8所示。

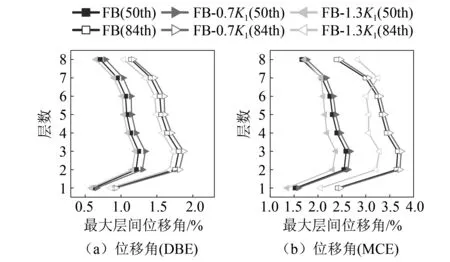
图8 VFD-SCB框架地震响应(K1)Fig.8 Seismic responses under different parameters (K1)

在DBE 作用下，随第一刚度的增大，结构各层的最大层间位移角减小，结构层间位移角小于2%，沿层高呈现均匀分布。在MCE作用下，随第一刚度的增大，结构位移角响应的减小幅度大于DBE作用下。结构此时的平均位移角大于2%，说明VFD-SCB已经进入坡面滑动段，结构仍表现出沿层高均匀分布的位移角，VFD-SCB具有良好的耗能性能。因此应提高加工精度以增大第一刚度，使结构层间位移角分布更加均匀。

4.3 支撑第三刚度的影响

与传统SCED不同，VFD-SCB在进入坡面后将呈现第三刚度，第三刚度主要由VFD的坡面角度和碟簧刚度确定，但过大的第三刚度对结构设计及成本提出更高的要求。相比于FB，对第三刚度分别降低和提升30%，记为FB-0.7K3，FB-1.3K3，分析支撑第三刚度对框架抗震性能的影响，如图9所示。

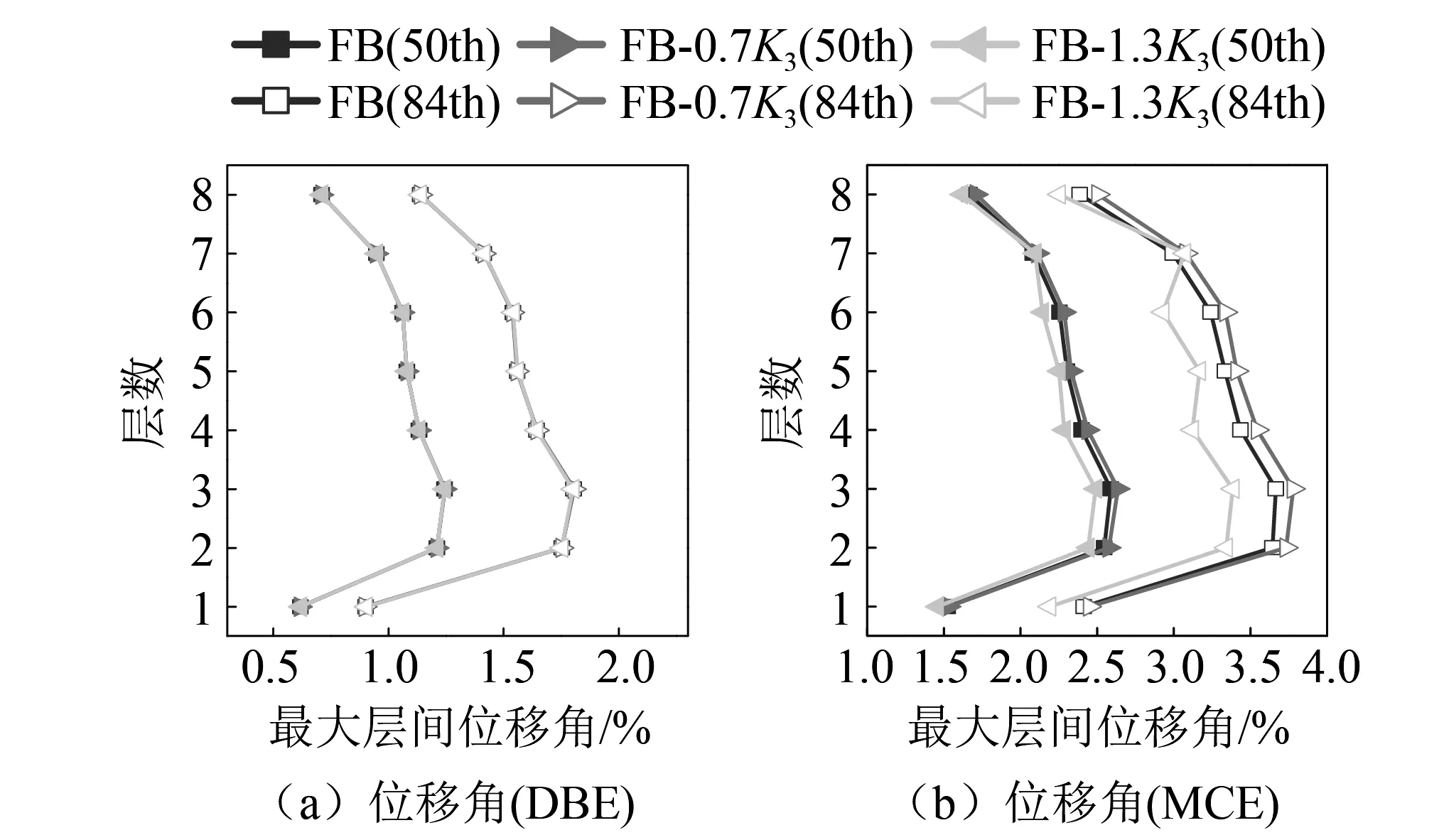
图9 VFD-SCB框架地震响应(K3)Fig.9 Seismic responses under different parameters (K3)

随着支撑第三刚度K3的增加，DBE下的层间位移角变化较小，因为支撑中的耗能器在DBE作用下位移角小于二次启动对应的2%位移角，支撑仅在平面段滑动，因此受第三刚度的影响极小。而在MCE下，框架中支撑二次启动，耗能器进入坡面滑动段。此时随支撑第三刚度的增加，结构的最大层间位移角减小。同时支撑第三刚度对底部楼层的层间位移角影响更为显著，第三刚度的增大使结构沿层高分布的位移角更加均匀。因此将第三刚度设置为基准模型的1.3倍以提升框架在大震下的耗能能力。

4.4 二次启动位移影响

在VFD-SCB中，耗能器坡面段滑动段的启动是实现多阶段抗震目标的关键。如果耗能器平面滑动段设计过大，可能导致结构在大震下支撑仍然处于平面滑动段，其效果与传统SCED相同。如果平面滑动段设计较小，坡面滑动段过早启动，造成支撑设计过于保守，过早进入坡面也给梁柱节点带来过大负担，对经济性要求更高。相对于FB，调整VFD-SCB框架中支撑的耗能器平面段长度使支撑的耗能器坡面滑动段开始于1.5%层间位移角和2.5%层间位移角处，记为FB-1.5θ，FB-2.5θ，分析支撑二次启动对框架抗震性能的影响，如图10所示。

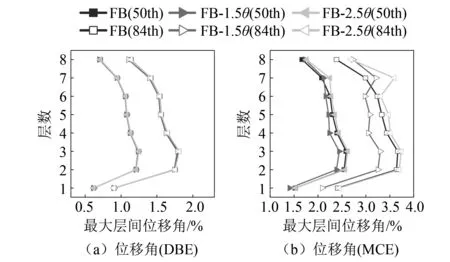
图10 VFD-SCB框架地震响应(θ)Fig.10 Seismic responses under different parameters (θ)

在DBE作用下，由于大部分结构位移角小于1.5%，因此结构各楼层50th位移角响应受二次启动的影响较小。由于支撑的提前启动使少数支撑在2.0%之前进入坡面滑动段，耗能能力增大，因此84th位移角响应随二次启动的提前而减小。在MCE作用下，FB-1.5θ和FB-2.5θ在7层的位移角均大于FB(基准模型)，这是由于当变摩擦在中震下启动时(FB-1.5θ)，会给节点带来过大负担，使梁柱节点产生破坏，加剧了结构上部楼层位移角；当变摩擦启动过晚时(FB-2.5θ)，VFD-SCB表现为传统自复位支撑，由于支撑耗能能力不足，使变形集中于结构中上部。因此二次启动位移设置为2%层间位移角即可满足结构的在地震下的变形需求。

4.5 碟簧预紧力影响

增大初始预紧力Np会增加耗能器平面段和坡面段的摩擦力，从而提高支撑整体耗能能力。但过大的Np对BFRP的初始预应力、碟簧的变形能力以及梁柱节点提出更高的要求。相比于FB，对Np分别降低和提升30%，记为FB-0.7Np，FB-1.3Np。由于调整碟簧预紧力会改变阻尼器的启动力，在BFRP筋的预应力不变时，会对支撑的自复位性能产生影响，因此支撑碟簧预紧力对框架位移角与残余位移角的影响，如图11所示。

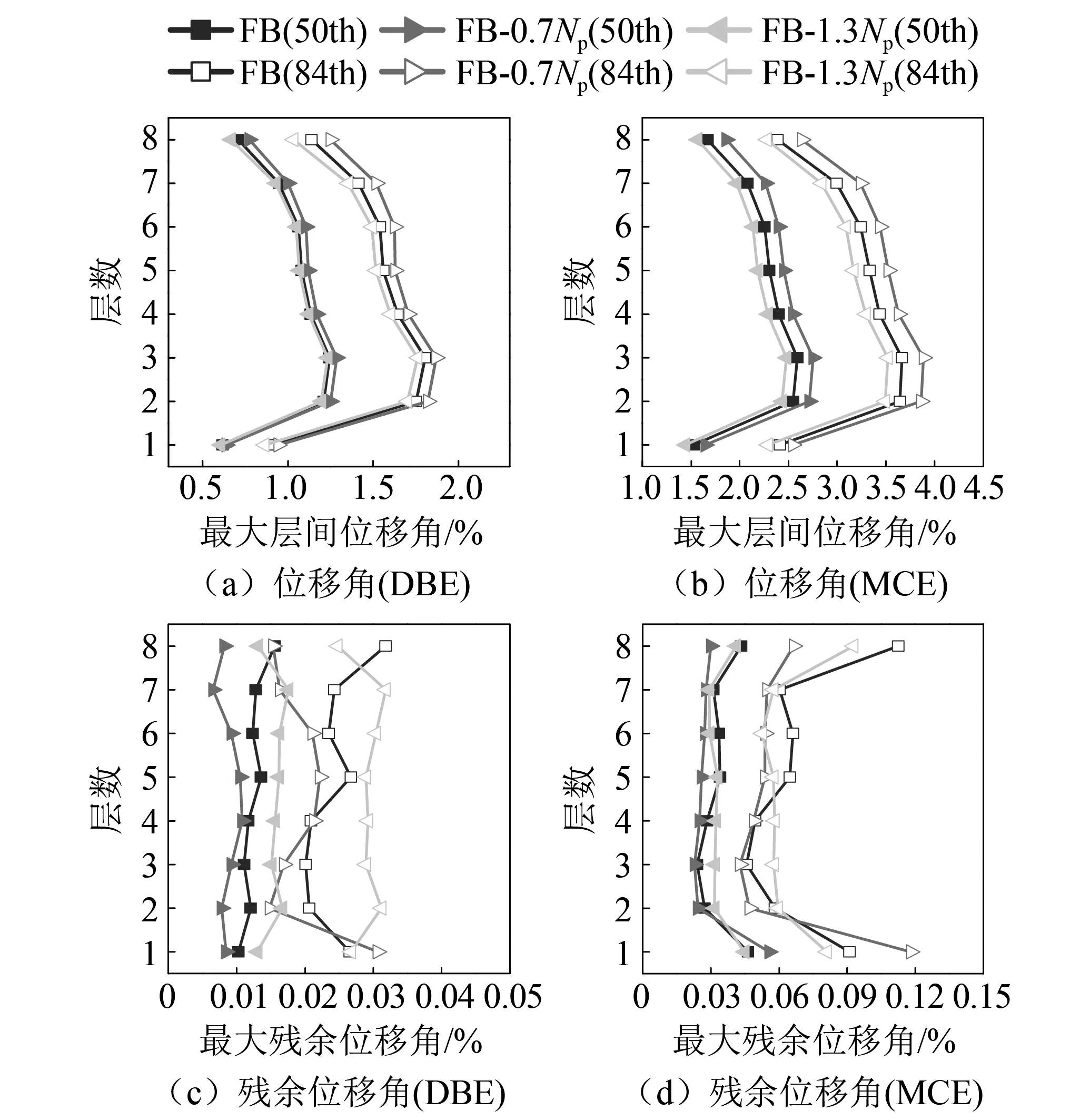
图11 VFD-SCB框架地震响应(Np)Fig.11 Seismic responses under different parameters (Np)

在DBE及MCE作用下，随着碟簧初始预紧力的增大，结构各层的最大层间位移角几乎成比例的减小，说明随着VFD-SCB耗能能力的提升，结构层间位移角减小。

由结构残余位移角可知，在DBE作用下，支撑表现出传统的旗帜形滞回，随着碟簧预紧力的增大，结构的残余位移角呈现略微增大趋势，但最大残余位移角仍小于0.04%。在MCE作用下，相比其余框架，FB-1.3Np具有较好耗能能力，因此其最大残余位移角小于其余两工况，同时残余位移角沿层高的分布更加均匀。因此在满足BFRP的初始预应力、碟簧的变形能力以及梁柱节点的前提下，建议增大碟簧预紧力为基准模型的1.3倍以提升结构的耗能能力。

5 结 论

为提升支撑钢框架在大震下的抗震性能，本文提出了具有二次启动的VFD-SCB。通过碟簧和坡面摩擦板的组合，实现了支撑变摩擦、变刚度的目标。利用有限元软件OpenSees对其滞回模型二次开发的基础上，研究了关键设计参数对VFD-SCB钢框架抗震性能的影响规律。本文的主要结论如下：

(1) 提出了一种随加载位移实现二次启动的VFD-SCB。通过VFD-SCB的工作机理，分析了其在平面及坡面摩擦段的力学性能，验证了支撑的变摩擦、变刚度的工作性能。

(2) 基于OpenSees软件，建立了考虑第一刚度修正的VFD-SCB滞回模型，通过与理论和试验结果的对比，验证了本文二次开发模型的有效性。

(3) 相比传统抗弯钢框架，VFD-SCB框架有效减小结构的位移角及残余位移角，使结构位移角沿层高分布更加均匀。

(4) 随VFD-SCB第一刚度、第三刚度、碟簧预紧力的增大、二次启动位移的减小，结构的层间位移角均减小。框架设计中需综合考虑支撑BFRP的初始预应力、碟簧的变形能力以及框架梁柱节点承载力以提升结构的抗震性能。