立体交叉隧道爆破振动影响因素正交试验研究

戴 轶， 刘家明， 张俊儒， 王智勇

(西南交通大学土木工程学院交通隧道工程教育部重点实验室，四川成都 610031)

随着我国国民经济的发展，交通设施需求日益增加，新建隧道数量逐年增多。随着众多交通隧道复线工程的修建，由于地质条件、既有建(构)筑物的限制以及地下空间综合开发的需求，不可避免地会出现许多近接或者交叉的现象。

立体交叉隧道作为近接隧道的一种，其围岩及衬砌的变形、应力变化都有着自身的规律特点[1]。目前，国内外学者在这方面已有了广泛的研究，同时也取得了一定的研究成果。龚伦等[2]结合新建隧道下穿既有隧道工程实例，采用数值模拟的方法，对既有铁路隧道受下穿引水隧洞施工的影响和铁路隧道结构的安全对策进行了研究。游步上等[3]利用FLAC3D程序分析隧道交叉段的变形行为，探讨不同应力场与不同岩石强度等参数对隧道交叉段应力变化情况。赵东平等[4]借助FLAC3D模拟计算了小净距空间交叉隧道的爆破振动，并结合GB 6722-86《爆破安全规程》中的安全控制振速，划分了新建隧道爆破开挖的影响范围。刘镇等[5]采用三维弹塑性有限元方法对上下交叉隧道盾构施工进行了分析，针对围岩条件及间距，探究新建正交盾构隧道下穿施工对既有隧道沉降的影响。王明乐等[6]以新建铁路隧道为背景，采用三维弹塑性有限元方法，对交叠隧道进行数值模拟，从而进行施工方案优化。靳晓光等[7]通过三维弹塑性有限元方法，结合实际工程，分析了横通道不同施工方案和动态施工过程对主隧道围岩与初期支护结构力学行为的影响。王海龙等[8]以新建京张高铁草帽山隧道下穿既有唐呼重载铁路北草帽山隧道交叉工程为背景，结合爆破振速的现场实测和经验公式理论分析，提出爆破施工方案。上述研究多是针对交叉隧道的静力影响因素，而立体交叉隧道工程中新建隧道对既有隧道爆破振动的动力学的影响因素方面的研究相对较少。

然而当立体交叉隧道净距较小时，新建隧道开挖产生的爆破振动难免会给予周边既有隧道的支护结构、内部设施以及所承担的交通营运造成一定程度的影响，甚至威胁到安全性。如日本的荻津公路隧道以及意大利的 LocooColio 公路隧道，国内的西康线响水沟隧道、流潭隧道等，都出现过由于新旧隧道净距较小而导致既有隧道衬砌结构开裂、剥落等危及行车安全等现象[9]。因此，研究立体交叉隧道不同爆破振动因素对既有线的不利影响，探究其内在联系，显得尤为重要。

在相关文献调查中，发现立体交叉隧道爆破施工存在多方面的影响因素：净距、围岩级别、埋置深度、交叉角度、开挖方法和支护方式等[10-12]。基于以上研究背景，本文基于数理统计学和正交性试验原理，设计多种正交试验工况，探究新建隧道对既有隧道爆破振动动力影响。通过试验，对既有线隧道正交段衬砌不同位置的振动速度进行极差分析，拟得到不同影响因素下新建隧道爆破振动对既有隧道的动力影响结果，可为立体交叉隧道设计施工提供一定理论依据。

1 试验方案设计

根据对立体交叉隧道爆破振动影响因素的文献调查发现，对既有隧道产生爆破振动影响的因素众多，其中部分影响因素相较而言敏感性较低。为此，本文主要针对4种重要影响因素进行研究，即：净距、围岩级别、埋深和交叉角度，主要影响因素及水平如表1所示。

从表1可以得到：立体交叉隧道对既有隧道的爆破振动影响为4个非支护因素，每种因素存在4个水平因子。则可将其视作一个的44正交试验，选取L16(45)的正交试验表，共设计了16种数值模拟试验工况，将最后一列设置为空列得到正交试验工况，如表2所示。

表1 主要影响因素及水平

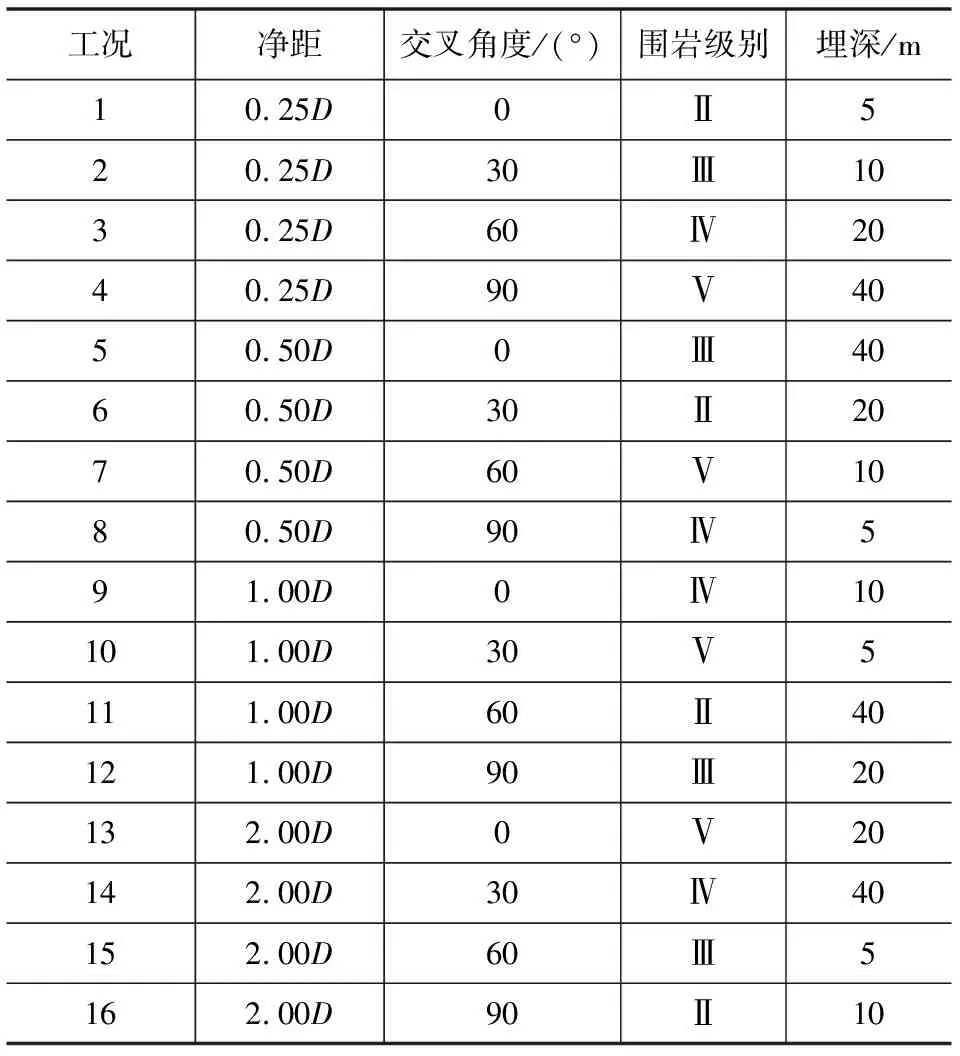
表2 正交试验工况设计

2 数值模拟计算

2.1 计算假定

采用有限差分数值计算方法进行3D计算，考虑交叉隧道相互影响长度[13]，16种试验工况数值模型长度取80 m，宽度取50 m，深度根据计算工况以及圣维南原理，并满足几点假定：

(1)围岩为弹塑性材料，服从Mohr-Coulomb屈服准则；初支、二衬为弹性材料。

(2)16种计算工况均为新建隧道下穿既有隧道。

(3)16种计算工况均采用上下台阶法进行静力计算，计算至交叉断面时进行动力计算，监测断面取既有隧道与新建隧道的交叉断面，监测点均设置在既有隧道内。

(4)模型两侧及底部均限制法向位移，地表为自由面。

(5)由于隧道下台阶爆破时临空面较大，爆破振动对既有线的影响远远小于上台阶爆破时的影响[14]。因此，数值计算只分析上台阶爆破振动影响。

2.2 爆破荷载

新建隧道开挖爆破荷载利用圣维南原理，采用等效荷载施加方式，将爆破柱状荷载建模方法等效成面荷载，即将作用在炮孔壁上的孔状爆破荷载等效成面荷载，这种等效方法不仅不需对掌子面炮孔建模，且计算容易收敛，提高计算效率。

将爆破荷载简化为由升压段和降压段组成的三角型脉冲荷载，荷载峰值应力Pmax[15]由式(1)进行求解。

(1)

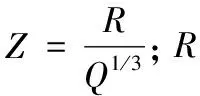
爆破荷载的升压段时间t0取10 ms，降压段时间t1取90 ms，总爆破时间为100 ms[16]。三角型脉冲荷载时程曲线如图1所示。

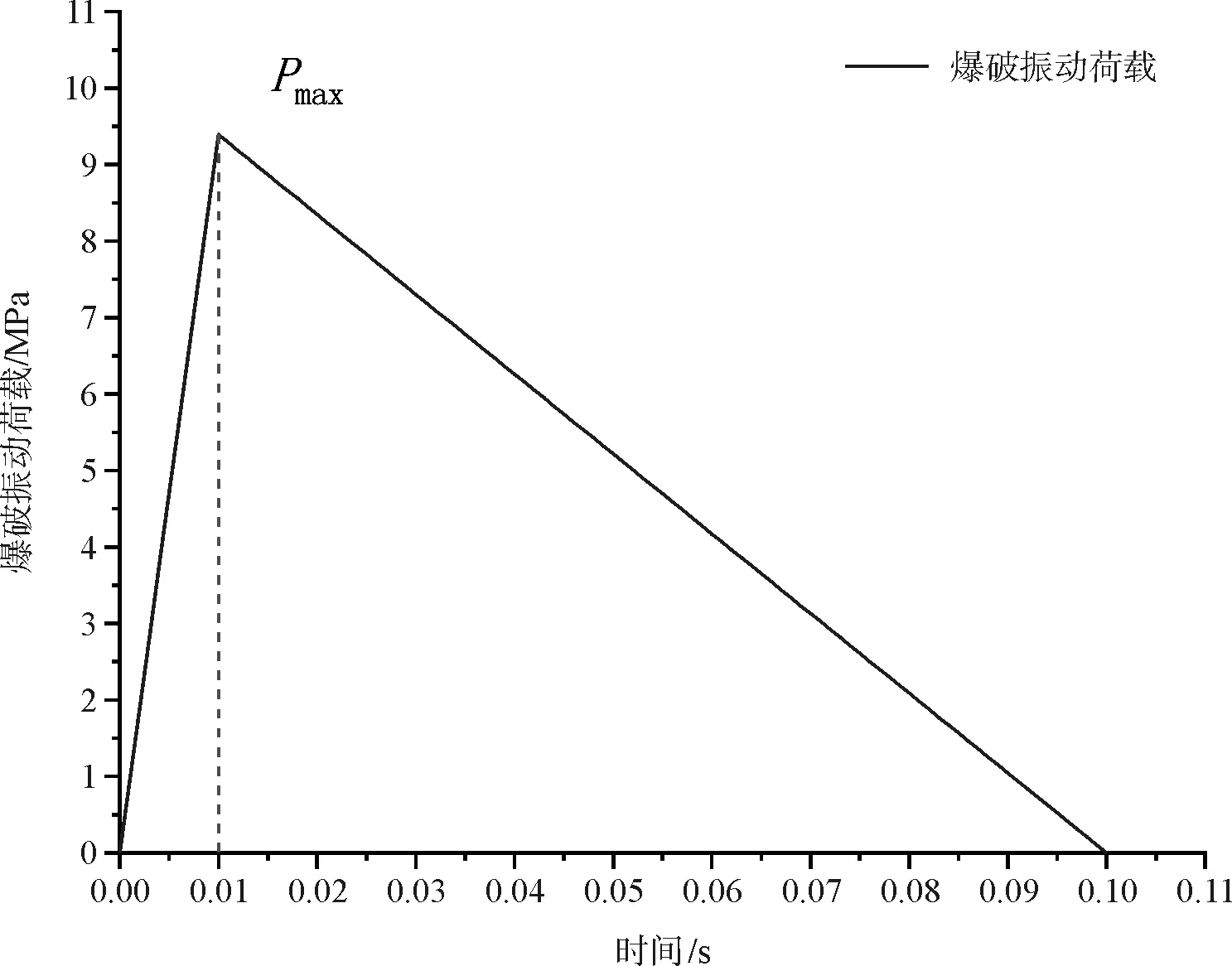
图1 三角型脉冲荷载时程曲线

2.3 材料参数

开始进行动力分析时，一般将围岩的参数进行一定的修正，围岩的变形模量按照Ed=8.7577ES0.5882修正[17]，泊松比按照νd=0.8νs修正[18]。主要材料参数参照相关手册选取[19]，如表3所示。图2和图3分别为部分计算工况模型和既有隧道监测点布置。

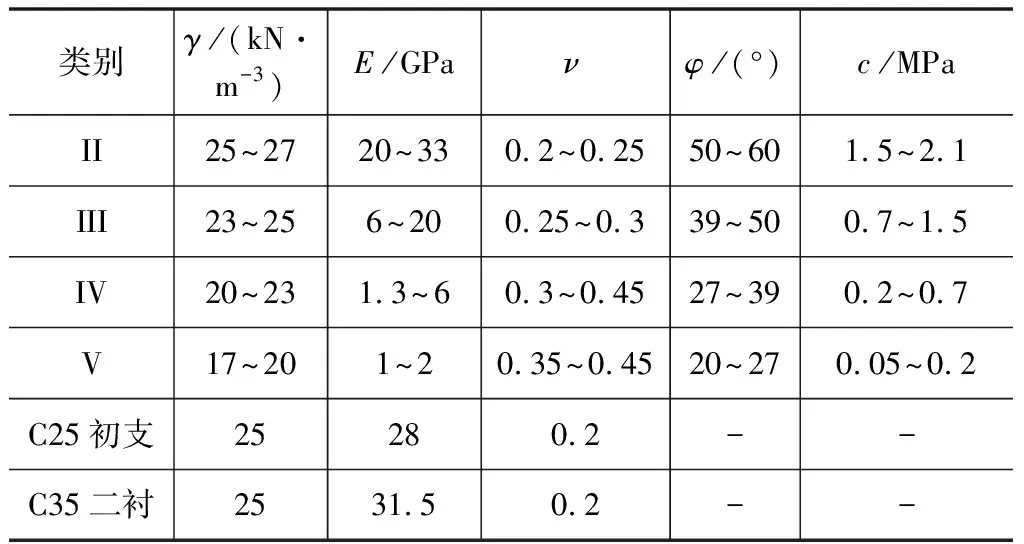
表3 围岩及支护材料物理力学参数

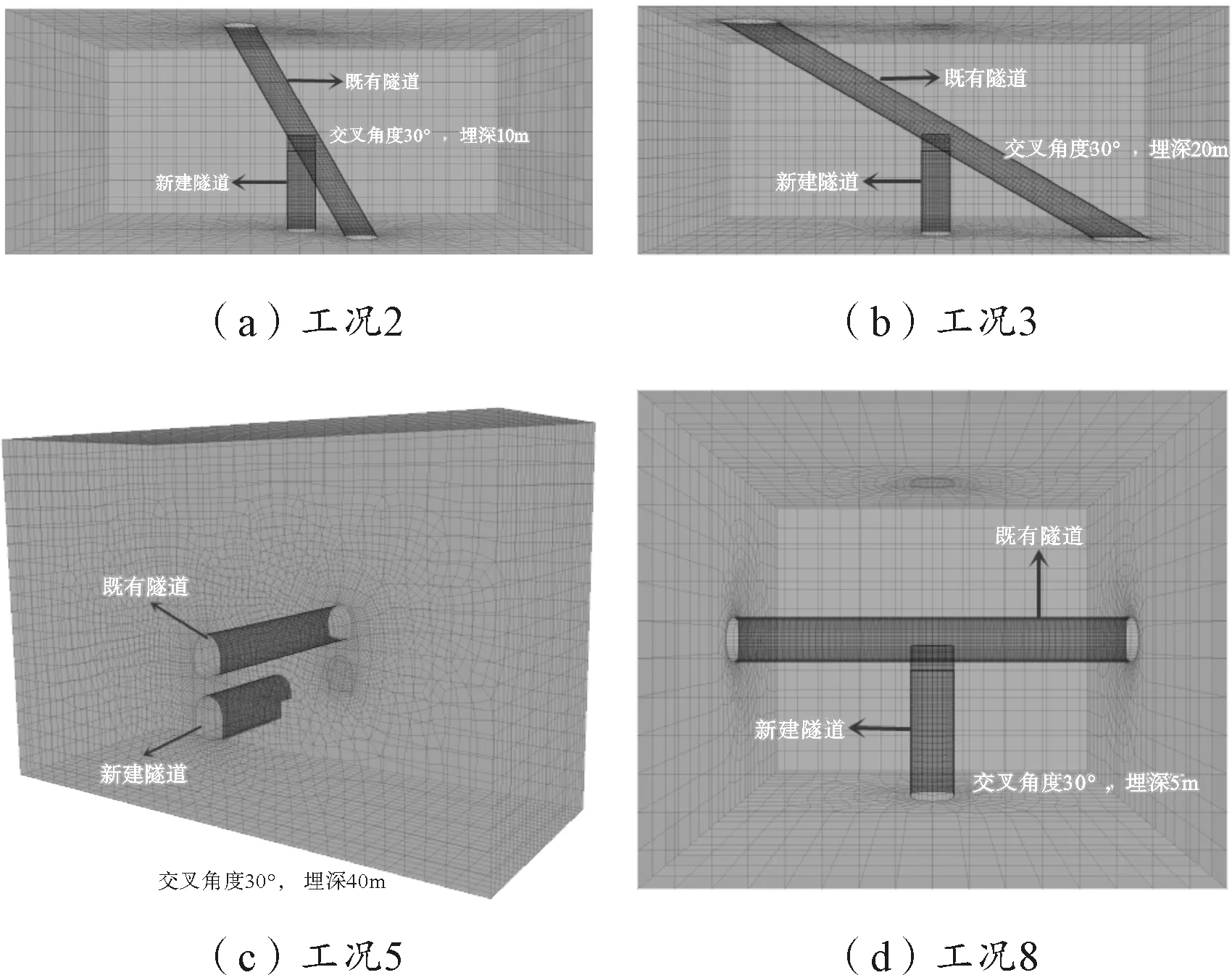
图2 部分计算工况模型

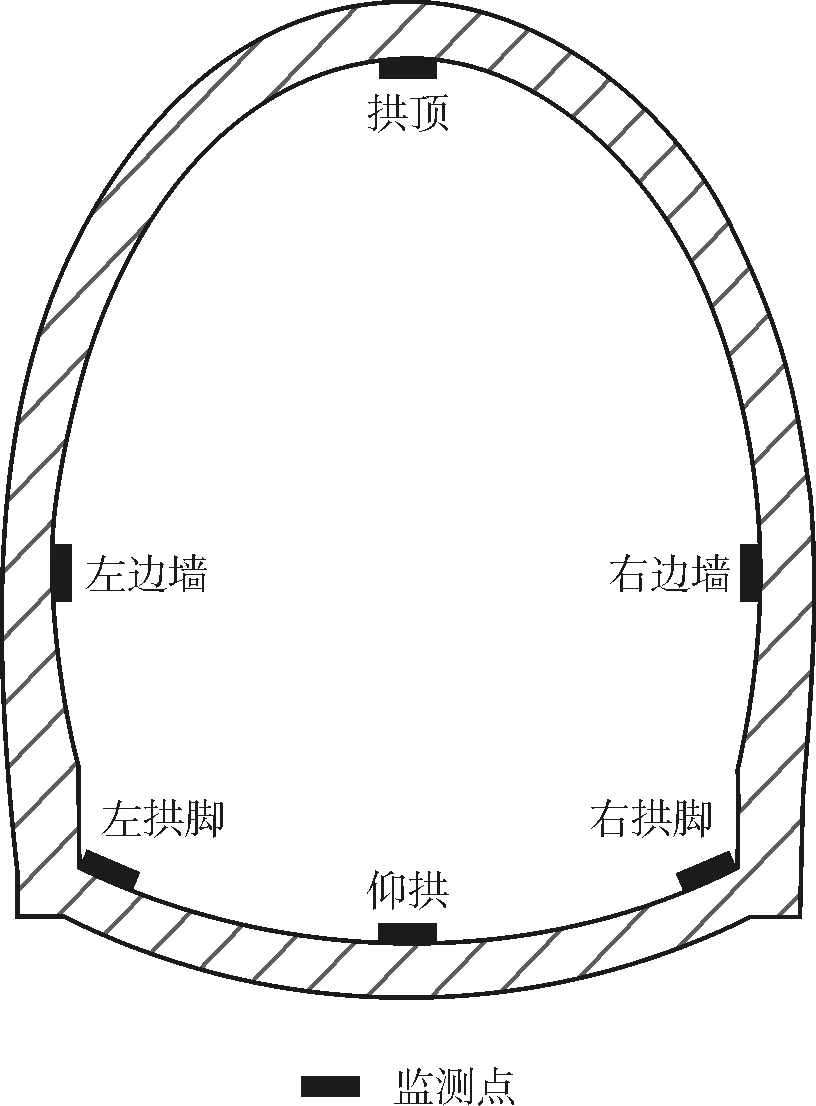
图3 既有隧道监测点布置

3 试验结果分析

3.1 计算结果

表4为各试验工况下，数值模拟动力计算阶段过程中，既有线隧道距离新建隧道爆破面最近的监测断面的拱顶、边墙、拱脚以及仰拱的最大振动速度。

爆破对既有结构的破坏因素众多，但目前已有的研究结果表明：建筑结构破坏程度受结构关键点振动速度的影响较大，以质点的峰值振速作为爆破振动安全的评定标准既准确又相对简单[20]。因而，计算结果分析仅对监测断面关键部位爆破振速进行(表4)。

表4 振速数值计算结果 单位：cm/s

3.2 结果分析

目前，对于正交试验结果分析方法，一是极差分析法；另一种方法是方差分析法。其中，极差分析法又称为直观分析法，具有直观形象、通俗易通的特点，是正交试验结果分析最常用的方法之一。因此，本文遂采用极差分析法，根据各计算工况下极差Ri的大小，判断各因素对试验结果的影响大小。判断原则：极差愈大，所对应的因素愈重要；由此可以确定出主、次要因素的排序。试验分析结果见表5和表6。

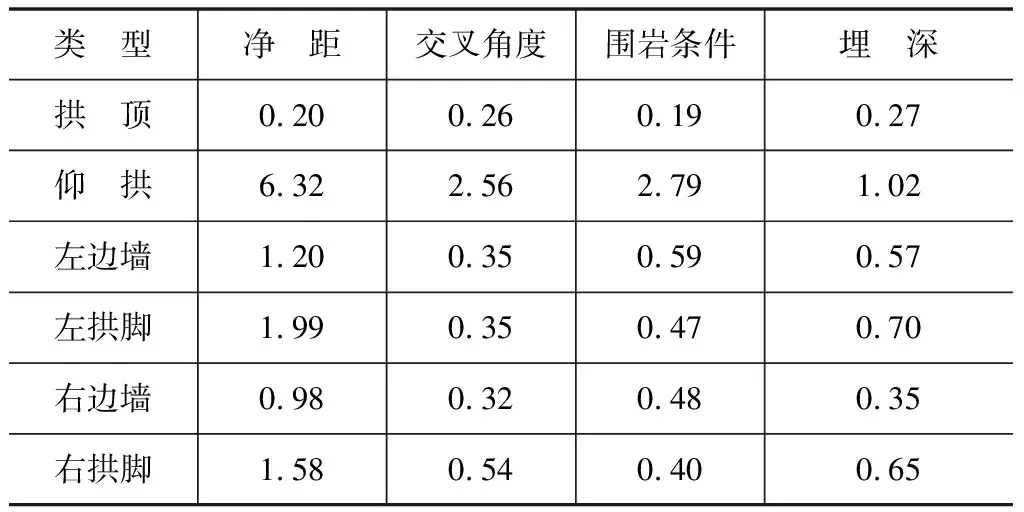
表5 各特征位置在各因素下的振速极差Ri 单位：cm/s

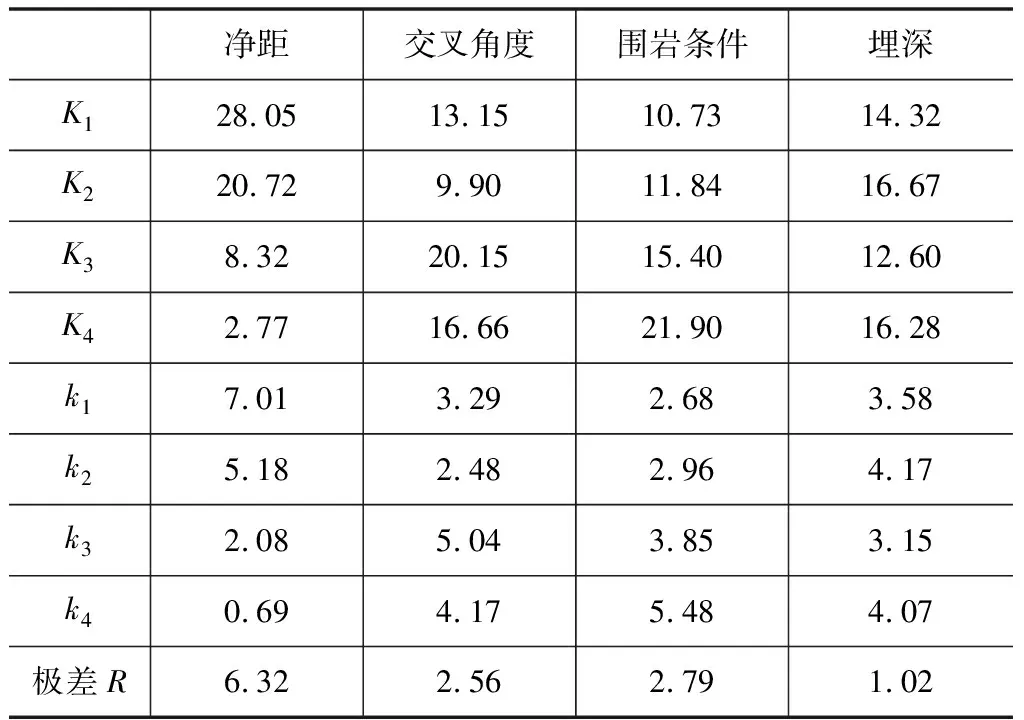
表6 仰拱极差分析 单位：cm/s

图4绘制了既有隧道各测点振速极差与各影响因素曲线图。由图可知，各影响因子对立体交叉处既有线监测断面仰拱振速极差敏感性排序为：净距(6.32 cm/s)、围岩条件(2.79 cm/s)、交叉角度(2.56 cm/s)、埋深(1.02 cm/s)，其中净距为重要影响因素，交叉角度和围岩条件为次要影响因素，埋深为一般因素。各影响因子对立体交叉处既有线监测断面拱顶振速极差敏感性排序为：埋深(0.27 cm/s)、交叉角度(0.26 cm/s)、净距(0.2 cm/s)、围岩条件(0.19 cm/s)，此时埋深和交叉角度为重要影响因素，净距和围岩条件为次要影响因素。由此可知，在既有隧道迎爆侧，净距为最主要影响因素。

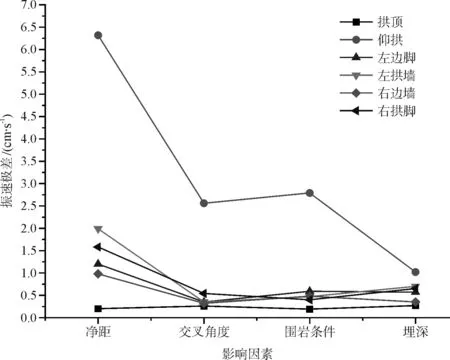
图4 振速极差与影响因素曲线

同时结合立体交叉处既有线监测断面两侧边墙和拱脚的振速极差进行分析，绘制振速极差与监测点位曲线，如图5所示。可以得到：既有线监测点距离爆源愈远，净距影响因素下各测点的振速极差越小。结合图4的分析结果可得：随着距离的增大，净距这一影响因子对既有隧道爆破振速的影响将显著减小。

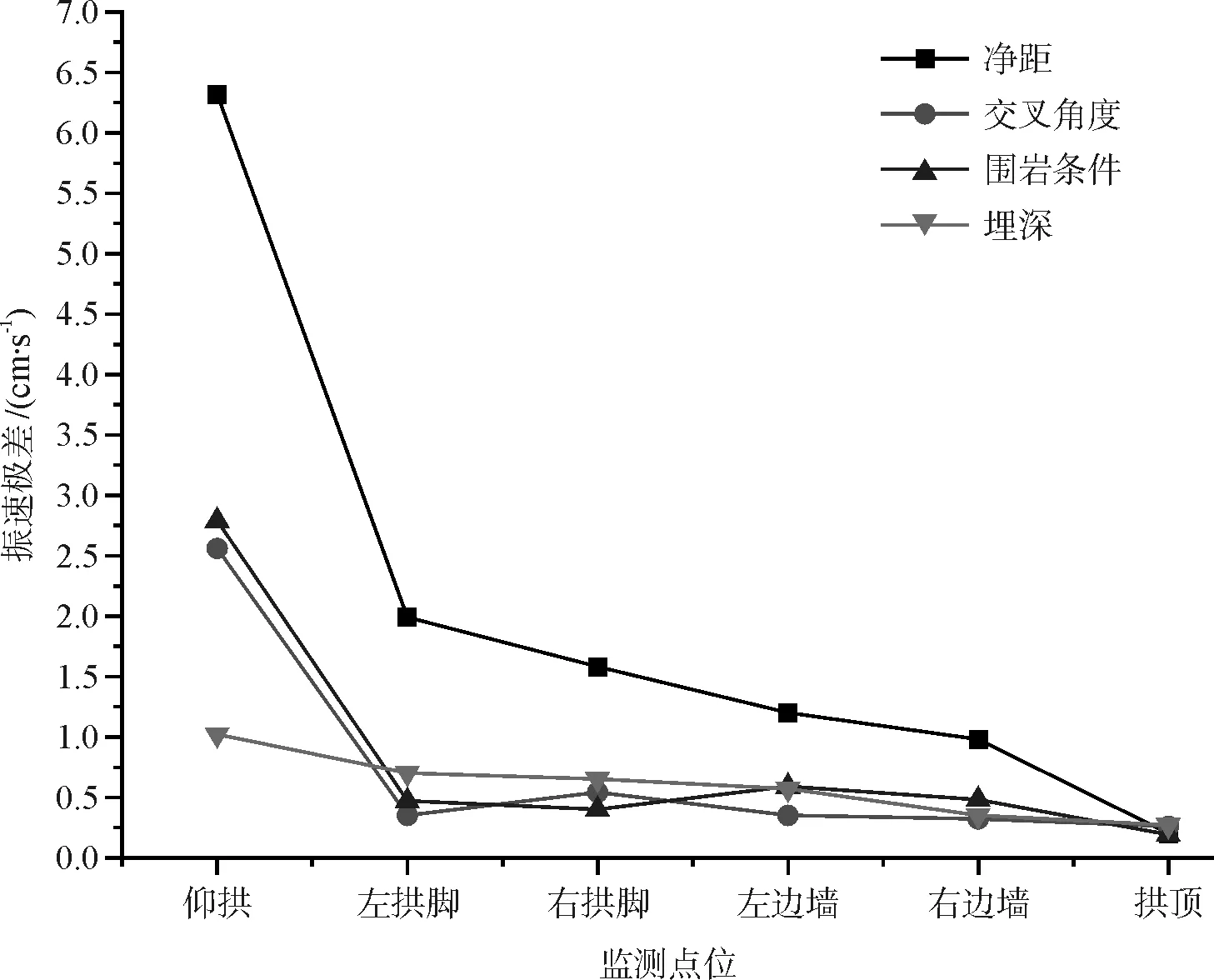
图5 振速极差与监测点位曲线

在既有隧道无损伤时，工程中往往仅关注迎爆侧振速的大小，因此针对立体交叉段既有线监测断面仰拱的振速极差计算过程进行分析(表6)。根据正交试验计算原理，在进行振速极差计算时，ki值越大，说明该因素下该水平对于试验结果的影响程度越大。

由表6可知，对于迎爆侧振速而言，净距越大，影响程度越小。交叉角度由0°变化到30°时，影响程度逐渐减小；由30°变化到60°时，影响程度逐渐增大；由60°变化到90°时，影响程度又逐渐减小。即随着角度的变化，影响程度呈现先减小再增大再减小的变化规律；围岩条件越差，影响程度越大；埋深的影响不是很显著。

4 结论

(1)在立体交叉隧道接近段，根据既有线隧道各部位的爆破振速情况下，在净距、交叉角度、围岩条件以及埋深4种影响因素中，净距为最主要影响因素，其他因素相较而言影响较小，而随着测点距爆源距离的增大，净距对各测点爆破振速的影响将显著减小。

(2)根据既有隧道迎爆侧振速，隧道净距越大，影响程度越小；随着交叉角度由0°变化至90°，影响程度先减小再增大再减小；围岩条件越差，影响程度越大；埋深的影响相对不显著。

(3)立体交叉段的既有线隧道仰拱处爆破振速，相较于其他部位测点数值较大，因此，在新建隧道施工过程中应重点监测，在既有线衬砌加固时可优先考虑；而拱顶的爆破振速测点数值最小，即受本文所述4种因素的影响有限，相比于其他部位更为安全。