5—10 µm 波段超导单光子探测器设计与研制*

陈奇 戴越 李飞燕 张彪 李昊辰 谭静柔 汪潇涵 何广龙 费越 王昊 张蜡宝 康琳 陈健 吴培亨

(南京大学电子科学与工程学院,超导电子学研究所,南京 210023)

高性能的中长波单光子探测器在红外天文和军事国防领域具有重要的研究价值,也是单光子探测技术领域的研究难点.超导纳米线单光子探测器在近红外波段已经展示出优异的性能,但如何进一步提高器件的探测截止波长λc 是一个受到广泛关注的话题.本文探讨了一种通过超导无序调控辅助提高λc 的方法,设计并制备出工作波段为5—10 µm 的超导单光子探测器.理论分析表明,增大衡量无序强度的主要评价因子即薄膜方块电阻Rs,将有利于增大λc,如当纳米线宽保持在30 nm 且Rs >380 Ω/square 时,可使得λc >10 µm.实验测得Rs 约为320 Ω/square 的Mo0.8Si0.2 红外器件在6 µm 波长上可以获得完全饱和的量子效率.此外,当器件工作在0.9ISW (ISW 为纳米线超导转变电流)的偏置电流下时,在10.2 µm 波长上的量子效率达到53%.

1 引言

作为诸多现代化高科技装备的眼睛,先进红外探测器受到了越来越广泛的关注.在极限灵敏探测领域,超导纳米线单光子探测器(superconducting nanowire single-photon detector,SNSPD)已在近红外波段展现了极好的工作性能,如系统探测效率大于98%[1,2]以及时间分辨率小于3 ps[3]等.理论研究表明,SNSPD 的工作波长可进一步覆盖中长波红外光谱,实现高性能中长波红外SNSPD 的研制对许多前沿科学技术领域具有重要的应用价值:喷气推进实验室(JPL)与国家标准与技术研究所(NIST)研究表明采用高性能的中红外SNSPD 可有效提高未来“起源号”太空望远镜上装载的系外行星传输光谱仪的工作稳定性[4];Chen 等[5]基于高时间精度和高光谱分辨率SNSPD 的中红外光谱仪系统揭示了分子科学领域的新规律;美国国防高级研究计划局(DARPA)在其“Invisible Headlights”项目中已联合麻省理工学院将打造一款基于中长波红外SNSPD 的全新无源3D 视觉传感器,来提高其军事装备的隐蔽性[6].然而,随着探测波长的增大,常规SNSPD 的量子效率ηi呈指数形式下降[7],如何有效提高SNSPD 在中长波红外波段上的ηi,成为了其发展方向上的一个关键性难点.

探测截止波长λc是表征SNSPD 量子效率ηi能够达到饱和的最长波长[8].当前研究表明,纳米线的超导能隙Δ和截面尺寸是影响SNSPD 探测截止波长λc的两大因素.一方面,减小Δ可以使相同能量的单光子在超导纳米线上破坏更多的库珀对.目前用于研制中红外SNSPD 的低能隙超导材料主要有WSi[9]和MoSi[10].另一方面,根据二流体模型,减小纳米线宽w可以使纳米线截面区域库珀对的总量减小,从而导致光吸收区域的超导序参量被大幅度抑制.前期研究中,我们将Mo0.8Si0.2超导纳米线的宽度减小到30 nm,在1.55—5.07 µm宽谱上获得了近乎饱和的量子效率[10].

在以上两种技术途径之外,本文研究发现超导薄膜的无序特性也是影响SNSPD 探测截止波长λc的一大因素.超导体的无序特性实际上描述了库珀对的局域化行为[11].一方面,当产生强无序现象时,库珀对之间的长程相干特性被破坏,使超导序参量离散化,超导体内部将变成一个个孤立的超导岛,最终导致超导-绝缘相变的发生[12,13].但另一方面,当无序的强度保持在一定程度内时,孤立的超导岛并不会产生,因此不会引起超导-绝缘相变.在此范围内,随着无序的增强,库珀对之间的库仑斥力增大,相互吸引力减小,使得破坏库珀对形成准粒子所需要的能量减小.此外,无序增强也会使得超导体的常温电阻率(或方块电阻Rs)增大.由Einstein-Smoluchowski 关系可知,超导体费米面上的电子态密度减小,最终导致相应的库珀对密度降低[14].从超导单光子探测的角度来看,超导薄膜无序特性的增强将导致光子激发产生的准粒子云的有效温度更高,从而增大诱导纳米线发生超导相变的概率.

由此,在新的技术途径中,可以考虑通过对超导薄膜无序特性的有效调控来达到增大SNSPD探测截止波长λc和量子效率ηi的目的.超导薄膜的方块电阻Rs是衡量其无序强度的一个主要评价因子,一般认为无序越强则Rs越大[15].因此,本文分析了在具有不同结构尺寸的SNSPD 中,Rs的大小对λc的影响.理论分析表明,在不同的线宽条件下,Rs增大将同步增大λc,这一理论预测在实验中也得到了论证.本文通过增大Mo0.8Si0.2薄膜的Rs进一步将相应SNSPD 的λc从低于5 µm 提高到了6 µm,同时在10.2 µm 波长上测得量子效率ηi达到53%.

2 理论分析

尽管SNSPD 的光探测微观机制仍缺乏完善的理论解释,但研究表明整个光响应过程常伴随着准粒子的倍增和扩散运动.因此,本文在理论分析中主要考虑准粒子的影响,基于唯象准粒子扩散模型可以得到SNSPD 的探测截止波长λc的计算表达式[16]

其中,K为光子在纳米线上的能量利用率(即用以有效破坏库珀对并激发产生准粒子的能量占总光子能量的比例),h为普朗克常数,c为真空中的光速,e为单位电荷量,Rs为超导薄膜的方块电阻,Δ为纳米线的超导能隙,w为纳米线的宽度,D为超导薄膜的电子扩散系数,τth为电子热化时间,IB为探测器的偏置电流,Idep为探测器的破对电流(IB理论上可以达到的最大值).为充分说明无序对λc的影响,本文将建立不同结构尺寸下λc与Rs的定量数学关系:λc=f(Rs,w).

在(1)式中,由于超导能隙Δ同样受到Rs与w的影响,因此在表征λc,Rs以及w三者间关系之前,需要解析三者之间的联系.首先,有研究表明Δ与探测器工作温度T以及纳米线超导相变温度Tc之间存在以下关系[17]:

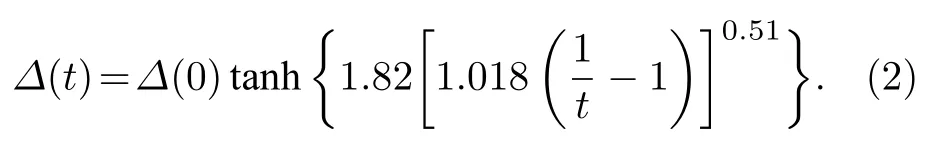
根据BCS 理论有Δ(0)=1.764kBTc,kB为玻尔兹曼常数,t为归一化温度因子,有t=T/Tc.这里假设探测器工作在0.3 K 的温度下,即T=0.3 K.通过分析无序与薄膜超导电性的关系,Ivry 等[18]得到了薄膜的超导相变温度Tc0、薄膜厚度d以及薄膜方块电阻Rs之间的数学关系:

式中,A和B均为常数拟合因子.以Mo0.8Si0.2超导薄膜为例,根据Li 等[19]的研究结果可得A和B拟合因子分别为63752 和1.42.

结合Simonin 模型关于Tc0与d之间关系的描述,有Tc0=(1–dmin/d),其中Tcbulk为体材料超导体的超导相变温度;dmin作为常数拟合因子,表示超导薄膜的最小厚度[20].Mo0.8Si0.2薄膜超导相变温度Tc0与薄膜厚度间的关系如图1 所示,采用Simonin 模型进行拟合可得到和dmin分别为7.8 K 和2.4 nm.此外,当超导薄膜制备成纳米线时,超导邻近效应的存在将导致纳米线的超导相变温度Tc低于Tc0.根据前期的研究成果,可得具有不同宽度w的超导纳米线的Tc与Tc0存在以下关系[21]:

图1 Mo0.8Si0.2 薄膜的超导相变温度Tc0 与厚度倒数1/d的关系,红色直线为Simonin 模型的拟合结果Fig.1.Relationship between the superconducting phase transition critical temperature Tc0 and the reciprocal of the thickness 1/d of the Mo0.8Si0.2 thin film.The red curve shows the fitting results of the Simonin model.

式中,ξ(0)为薄膜在0 K 下的超导相干长度,wn表示纳米线两侧由无序等因素造成的正常态区域总宽度.对于Mo0.8Si0.2超导薄膜而言,ξ(0)=4.5 nm,wn=6.0 nm.最终结合(3)式和(4)式可得到Rs与纳米线宽w对超导纳米线的Tc的影响:

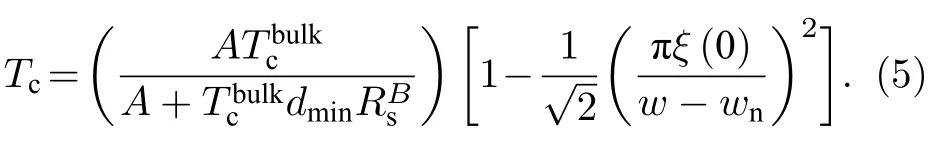
如图2(a)所示,在保持纳米线宽w不变的情况下,超导薄膜方块电阻Rs的增大将导致纳米线的超导相变温度Tc减小.如当w减小到30 nm 且Rs>100 Ω/square 时,Tc<5 K,进一步增大Rs>300 Ω/square 时,Tc将减小到3 K 以下,这对探测器的工作温度提出了更高的要求.将(5)式代入到(2)式中,即可获得Δ,Rs与w之间的关系.此外,当探测器具有较高的超导临界转变电流时容易获得高的信噪比,有利于光响应脉冲的读取.因此本文研究了Rs与w对探测器超导破对电流Idep(即超导临界转变电流的理论最大值)的影响.这里参考Kupriyanov-Lukichev 模型来计算纳米线的破对电流[22]:

其中,pd(t)表示一个与温度相关的修正因子.如图2(b)所示,随着w的减小以及Rs的增加,呈现下降趋势.为便于直观地分析,图2(b)设置了白色和黄色两条刻度线,分别表示为3 µA 和10 µA 的情况,在刻度线上方且越远离刻度线,越小.在保持不变时,随着w的减小,相应的Rs将加速下降.如当≥ 3 µA 时,若w=50 nm,则相应的Rs可持续增大,最大可到500 Ω/square;若w=30 nm,则Rs最高不能超过340 Ω/square.

图2 (a) 超导薄膜方块电阻Rs 与纳米线宽w 对纳米线的超导相变温度Tc 的影响;(b) 超导薄膜方块电阻Rs 与纳米线宽w 对纳米线的破对电流的影响, 随着Rs 的增大以及w 的减小而降低,图中白色和黄色虚线分别表示为3 µA 和10 µA 时的计算结果Fig.2.(a) Effects of the film sheet resistance Rs and the nanowire width w on the superconducting phase transition temperature Tc;(b) effects of Rs and w on the depairing current ,it can be shown that decreases with increasing Rs and decreasing w,and the white and yellow dashed lines represent the calculation results of 3 µA and 10 µA,respectively.

结合前面的分析,为进一步表征超导薄膜方块电阻Rs与纳米线宽w对SNSPD 探测截止波长λc的影响,本文评估了薄膜的电子热化时间τth,根据Zhang 等[23]的研究结果,非晶超导薄膜的电子热化时间τth与薄膜超导相变温度Tc0之间存在关系:τth=αTc0–1.5,其中常数因子α=515.74 ps⋅K1.5.如图3(a)所示,当SNSPD 的最大偏置电流IB可达到时,在不同的线宽条件下,Rs越大可使λc越长.其中绿色、黄色以及白色三条虚线代表λc分别对应2.5,5.0 和10 µm 三个波长的结果,由此可知在w>25 nm 的条件下,当保持λc的增量不变时,w越大将导致相应的Rs所对应的增量越大.由此说明当超导薄膜的方块电阻不易大幅度调控时,较窄的超导纳米线在探测中长波红外光子时更具优势.而对于常规SNSPD (w>50 nm且Rs<400 Ω/square)而言,在避免器件结构等因素压缩超流从而保证较高归一化偏置电流(IB/)的前提下,探测器可在中红外波段(>2.5 µm)上获得饱和的量子效率.此外,当w<25 nm 且保持λc不变时,线宽的微小变化将导致相应的Rs大幅度涨落,如当λc=10 µm 时,w=25 nm 所对应的Rs=280 Ω/square,而当w降低了2 nm 后,对应的Rs将低于150 Ω/square.在不考虑制备工艺的前提下,理论计算表明,当w减小到20 nm 且Rs≥ 450 Ω/square 时,λc将超过150 µm.

为分析探测器在较低偏置电流下的结果,本文将最大偏置电流IB降低到时,得到λc,Rs与w的关系(图3(b)).与高偏置电流相比,低偏置电流下要获得相同的探测截止波长,探测器对Rs以及w的要求更加苛刻,如当Rs<500 Ω/square时,要使得探测器的λc增大到10 µm,所需要的纳米线的宽度将低于25 nm,这对器件制备工艺提出了巨大的挑战.此外,能看到此时对于常规SNSPD而言,λc主要分布在近红外波段,因此常规SNSPD难以在中红外波段上获得饱和的量子效率.

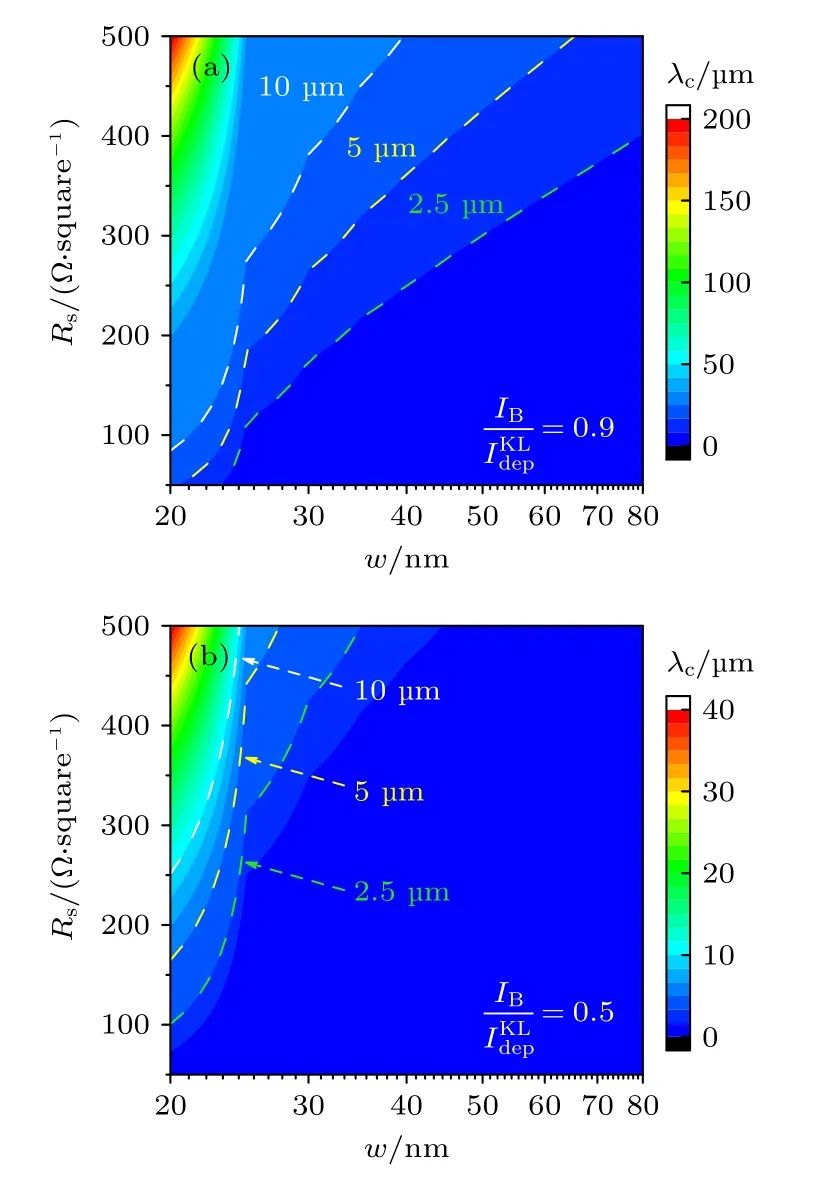
图3 (a) 当SNSPD 的最大偏置电流IB可达到时,超导薄膜方块电阻Rs 与纳米线宽w 对SNSPD 探测截止波长λc 的影响;(b) 当SNSPD 的最大偏置电流IB 降低到 时,Rs 与w 对λc 的影响 (图中绿色、黄色以及白色三条虚线分别表示三个λc 的刻度线,如当(w,Rs)的坐标点处于白色虚线上方时,λc >10 µm)Fig.3.(a) Effects of the film sheet resistance Rs and the nanowire width w on the cutoff wavelength λc when the maximum bias current IB of the SNSPD can reach (b) effects of Rs and w on λc when the maximum IB can only reach (Green,yellow,and white dashed lines represent the scale lines of the three λc values.For example,if the coordinate point of (w,Rs) stays above the white dashed line,λc >10 µm).

总的来说,通过对超导薄膜无序的定量调控(增大Rs),可有效增大λc,在高归一化偏置电流的条件下,可使得SNSPD 的探测截止波长覆盖可见至远红外波段.在λc的温度相关性方面,研究表明当SNSPD 的工作温度T<0.1Tc时,λc可认为是一个与T无关的量.然而,从器件制备与应用的角度上看,持续的增大Rs将带来探测器的超导相变温度Tc以及超导破对电流下降,且这种下降趋势在w较小的情况下尤其明显,这实际上并不利于探测器的正常工作以及信号读出.因此,在保持SNSPD 具有较大λc的前提下,如何提高Tc和对推进SNSPD 在中长波红外波段上的发展具有关键的科学价值和应用价值.目前国内外相关研究单位普遍采用稀释制冷技术以及复杂低温读出电路来解决中长波红外SNSPD 低Tc以及低信噪比的问题,取得了一定的效果.然而,在推进探测器小型化和低成本的道路上,中长波红外SNSPD仍然面临着一段很长的路.

3 实验结果与讨论

3.1 器件制备与测量

前期我们采用Mo0.8Si0.2超导薄膜所制备的SNSPD 在1.55—5.07 µm 的红外波段上测得量子效率超过97%,然而测量得到器件的探测截止波长λc低于5 µm,相应Mo0.8Si0.2薄膜的方块电阻Rs=248.6 Ω/square,纳米线宽度w=30 nm[10].根据第2 节的理论分析,为了进一步提高器件的探测截止波长,我们适当增大Mo0.8Si0.2薄膜的无序强度,即在相同的测量条件下将薄膜的方块电阻Rs进一步增大到320 Ω/square,同时保持线宽w不变.探测器的总体结构如图4(a)所示,为有效降低纳米线上缺陷引入的概率以达到减小超流压缩带来的不利影响,本实验设计器件的核心光探测单元为一条10 µm 长、30 nm 宽的超导纳米线.核心光探测单元动态电感小而使得响应脉冲能量主要集中在高频区域,因此在读出电路中难以对电脉冲进行有效滤波而保证较高的信噪比.为解决这一问题,本实验在核心光探测单元电流输入端增加了一段脉冲信号展宽结构,具体由180 nm 线宽,500 nm周期,30 µm × 30 µm 面积的蜿蜒纳米线组成.

图4 (a) 器件结构图,主要包含用于信号脉冲展宽的蜿蜒纳米线结构和响应红外光子的窄纳米线,这里为避免窄纳米线在制备过程中发生漂移,在窄纳米线上增加了多个“十字”结构;(b) 信号脉冲展宽蜿蜒纳米线的局部SEM 图,纳米线宽为180 nm;(c) 窄纳米线的局部放大图;(d) 窄纳米线的局部SEM 图,测量得到纳米线的宽度为30 nmFig.4.(a) Structure diagram of the detector,which mainly includes the signal pulse-broadened meander nanowire and the narrow nanowire that detects the infrared photons,many cross structures were added to avoid the drift behavior of narrow nanowire during the nanofabrication;(b) SEM image of the signal pulse-broadened meander nanowire,the measured nanowire width is 180 nm;(c) local magnification image of the narrow nanowire;(d) SEM image of the narrow nanowire,the measured nanowire width is 30 nm.

图4(b)为脉冲信号展宽结构的局部扫描电子显微镜(scanning electron microscope,SEM)图,实际制备得到的蜿蜒纳米线宽度与设计值保持一致.从电流偏置方面看,即使光探测单元上的偏置电流达到其临界值,蜿蜒纳米线上的偏置电流仍不超过相应临界值的1/6,因此在实际测量过程中可忽略蜿蜒结构带来的计数.光探测单元与脉冲信号展宽结构的制备在相同厚度的Mo0.8Si0.2薄膜上进行.采用聚氢倍半硅氧烷(hydrogen silsesquioxane,HSQ)负胶进行电子束曝光,在显影过程中,为防止窄纳米线出现漂移现象,本实验在窄纳米线上增加了多个“十字”结构以达到增大窄纳米线与衬底之间黏附力的目的,如图4(c)所示.窄纳米线上的每个“十字”结构之间间距为750 nm,在窄纳米线横向方向上,“十字”的宽度为440 nm.在“十字”中心区域,本文参考保角变换理论设计了优化圆角,从而使得该中心区域处不会出现超流压缩的现象.电子束曝光得到的纳米线结构通过反应离子刻蚀转移到Mo0.8Si0.2薄膜上,采用SF6作为刻蚀气体,标准状况下气压流量为40 mL/min,采用CHF3作为钝化气体,标准状况下气体流量为20 mL/min,在4 Pa 气压、80 W 功率的环境下刻蚀32 s,最终得到目标器件结构.图4(d)为实际制备得到的核心光探测单元的局部SEM 图,与设计结构保持一致,窄纳米线的测量宽度为30 nm.

实验分别测量了SNSPD 在6.0 µm 和10.2 µm两个波长上的量子效率,图5 为实验中采用的红外SNSPD 测量示意图.选择了两种类型的光源,其中采用冷红外黑体源(1500 K 工作温度,氮化硅发光材料,美国海洋光学仪器生产)用于辐射6.0 µm波长的光信号.采用量子级联激光器辐射10.2 µm中心波长的光信号,光源输出光谱宽度小于10 nm,激光发散角为5.5 mrad,工作温度恒定在25 ℃,最大辐射功率可达到毫瓦量级.光源产生的红外信号通过一段长度可调的光学套筒后形成的光斑尺寸增大,可降低器件光耦合的难度.可调中性密度衰减器用于调控出射光功率的衰减倍率,光信号经衰减后通过窄带滤波片(中心波长分别为6.0 µm和10.2 µm)以及ZnSe 光学窗口进入到稀释制冷机内部,再经过一级光密度Od=3 的固定衰减器后,最终到达SNSPD 的光敏面上.实验中,采用一个已串联100 kΩ 电阻的低噪声电压源给SNSPD提供电流偏置,SNSPD 吸收单光子并将其转化为一个电脉冲信号,电脉冲信号通过外部电路中的低噪声常温放大器(型号AU1338,0.3—350.0 MHz工作频带,美国MITEQ 公司生产,增益大于70 dB)进行放大,并由计数器(型号SR400,美国Stanford Research Systems 公司研制)采集读出,从而完成一次光子探测.

图5 红外SNSPD 测量示意图,红外光源输出的信号光通过光学套筒、可调中性密度衰减器、窄带滤波片、稀释制冷机的ZnSe 光学窗口以及制冷机内部的固定衰减器(光密度Od=3),最终覆盖SNSPD 的光敏面.SNSPD 吸收单光子并将其转化为一个电脉冲信号,电脉冲信号通过外部电路进行放大并读出,从而完成一次光子探测Fig.5.In the measurement diagram of the infrared SNSPD,the signal photons are emitted from the light source and finally arrive at the active area of the detector through the optical sleeve,the adjustable neutral density attenuator,the narrow band filter,the ZnSe optical window of the diluted refrigerator,and the fixed attenuator inside the refrigerator (with an optical density Od=3).The SNSPD absorbs one photon and converts it to an electrical pulse,and the pulse is amplified and read through the external circuit;thus,a photon detection event is finished.

3.2 器件测量结果

在50 mK 的温度下,实验首先测量了SNSPD对6.0 µm 波长的光探测结果,如图6 所示.量子效率ηi通常定义为探测器吸收一个光子对应产生一个可探测电脉冲信号的概率,当一个光子对应一个电脉冲信号时,可认为探测器的量子效率达到饱和.在SNSPD 探测技术中,定义ηi=Pc/Ps,其中Pc为探测器的光子计数率,而Ps表示光子计数率达到饱和(不再随偏置电流的变化而变化)状态下的结果.实验中,Pc=CR–Bc,CR为探测系统产生的总的计数率,包含了光子计数率以及背景计数率Bc.

图6 SNSPD 在6.0 µm 波长上的量子效率ηi 以及背景辐射计数Bc 随归一化偏置电流IB/ISW 的变化关系,红色曲线表示Fano 涨落理论对实验结果的拟合,实际测到的最大量子效率可达到完全饱和Fig.6.Normalized bias current-dependent quantum efficiency ηi and background count Bc of the SNSPD at 6.0 µm.The red curve represents the fitting result based on the Fano fluctuation theory.

实验中首先测量了Bc的大小.测量方法如下:关闭光源并将稀释制冷机的窗口做电磁屏蔽,进而扫描得到Bc随偏置电流IB的变化关系.从图6 可以看到,Bc随着偏置电流IB的增大具有一定的饱和趋势,且Bc的最大值不超过103counts/s.由此表明,组成Bc的两大因素中,由温度为300 K 的环境产生的红外背景辐射计数率占据了主要部分,而器件的本征暗计数较少,这是因为受磁涡旋运动的影响,本征暗计数随IB的增加往往呈现出指数上升的趋势[24].当IB接近临界转变电流ISW时,器件的Bc并没有明显的激增,推测可能是因为在mK 量级低温下,磁涡旋的运动受到了抑制.

此外,在量子效率ηi的测量上,随着偏置电流IB的逐渐增大,SNSPD 在6.0 µm 波长上的ηi逐渐增大至完全饱和状态,并呈现出一个明显的“S”形曲线变化形式.由于红外黑体源较大的发散角以及在6.0 µm 波长上较弱的辐射功率,使得单位时间内实际到达SNSPD 光敏面上的光子数较少,因而SNSPD 的饱和光子计数率Ps仅达到103counts/s量级,与背景辐射计数率Bc相当.此外,受Bc以及入射光功率涨落的影响,在不同的偏置电流IB下实际获得的Pc在逐渐达到饱和的过程中也出现了涨落.根据Kozorezov 等[25]的研究结果,Fano涨落现象将导致纳米线上光响应过程中传递给准粒子的能量存在不确定性,因而使得量子效率ηi与归一化偏置电流IB/ISW之间存在以下关系:

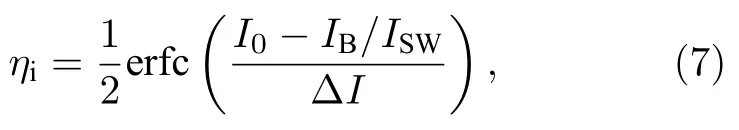
其中,I0=Ic0/ISW,Ic0表示当Pc/Ps=0.5 时所对应的偏置电流;ΔI=ΔIB/ISW,ΔIB=IB1–IB2(对 于IB1,ηi=80%;对于IB2,ηi=20%),表 示ηi在偏置电流上的转变宽度.红色曲线表示Fano涨落理论对实验结果的拟合,根据拟合结果可得到I0=0.81,ΔI=0.1.理论对实验结果的合理解释表明,Fano 涨落机制在中长波红外SNSPD 将光信号转化为电信号的过程中扮演了重要的角色.

当SNSPD 的探测波长增大到10.2 µm 时,再次测量ηi随偏置电流的变化关系.当归一化偏置电流IB/ISW超过0.7 以后,SNSPD 的光子计数率Pc快速增加但未出现饱和,因此难以直接得到Ps的实际值.将(7)式等效变化可得到:Pc=Ps/2 ×erfc[(I0–IB/ISW)/ΔI],增加Ps为拟合因子.经过最佳拟合后可以得到Ps=5300 counts/s,I0=0.9,ΔI=0.1.进一步,基于ηi=Pc/Ps关系可知ηi随归一化偏置电流的变化关系,如图7 所示.

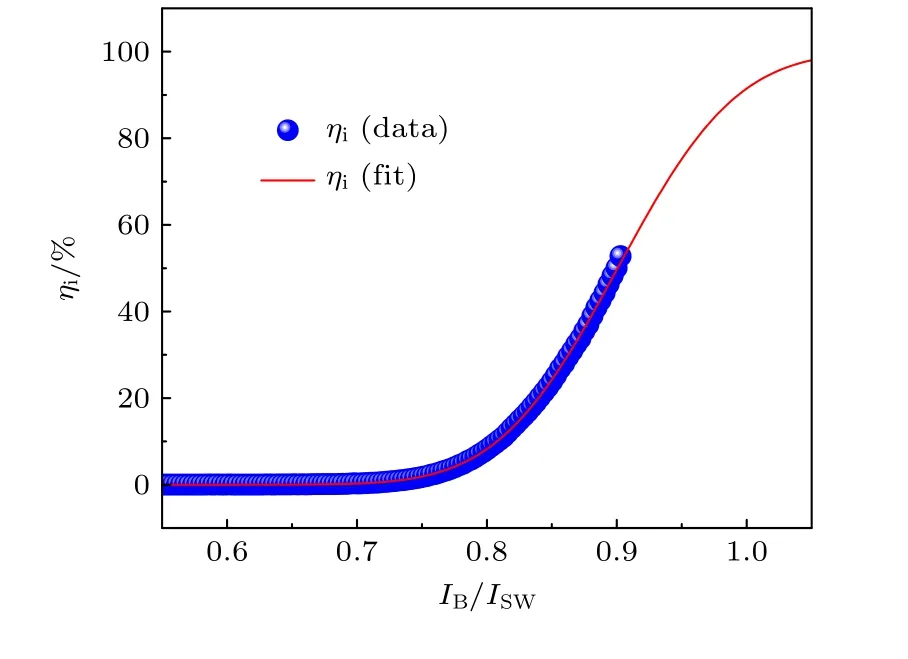
图7 SNSPD 对10.2 µm 波长的量子效率随归一化偏置电流的变化,红色曲线是Fano 涨落理论对实验结果的拟合Fig.7.Normalized bias current-dependent quantum efficiency ηi of the SNSPD at 10.2 µm.The red curve represents the fitting result based on the Fano fluctuation theory.

从实验结果可得当IB/ISW=0.9 时,ηi达到53%.研究发现,在实验中由于电路出现不规律振荡的原因,IB无法正常偏置到0.9ISW以上.通过Fano 涨落理论可以预测,IB/ISW=1 时,ηi可达到92%.因此,在未来的工作中,我们将努力克服读出电路不规律振荡的难题,从而在光响应测量中提高IB的偏置上限.

综上,本文从实验的角度对无序增大SNSPD探测截止波长λc的理论预测进行了论证.通过增大薄膜方块电阻Rs,λc已从前期低于5 µm 的基础上增大到了6 µm,同时在10.2 µm 的波长上也展现了ηi可达92%的探测潜力.由此可预测在超导能隙以及器件结构尺寸调控之外,无序调控将有可能成为研制高性能中长波红外SNSPD 的另一有效技术方案.而对于如何实现无序的可控研究,除了减小薄膜厚度之外,目前其他技术方法包括:纳米多孔研究[26]、层状缺陷引入[27]、薄膜组分比例调控[28]以及离子注入[29]等.如何寻找可行且最优的技术方法,是一个亟待解决的难题.

4 结论

本文从无序出发提出了增大SNSPD 探测截止波长λc的技术方法,并进一步讨论了无序以及尺寸变化对λc的影响.研究表明,超导薄膜方块电阻Rs的增大将同步增大λc,尤其当纳米线宽w较小时,λc的增大速率更快.如在IB/=0.9,w=30 nm 且Rs>380 Ω/square 时,λc>10 µm.在实验方面,本文制备了常温方块电阻Rs,约为320 Ω/square 且线宽w=30 nm 的Mo0.8Si0.2红外SNSPD,将器件工作波段扩展到了5—10 µm.在6.0 µm 波长上SNSPD 可获得完全饱和的量子效率ηi,在10.2 µm 长波红外上ηi达到53%,当排除超流压缩的影响时,ηi理论上最高可达到92%.此外,如何平衡器件工作温度、信噪比二者与λc之间的关系以及探索最优的无序调控技术,是中长波红外SNSPD 未来发展中需要解决的两大难题.