膝区宇宙线广延大气簇射次级成分的特征*
张丰 刘虎 祝凤荣
(西南交通大学物理科学与技术学院,成都 611756)
膝区反映了银河系宇宙射线源加速粒子能力的极限或银河系对宇宙线束缚能力的极限,分成分能谱的测量是理解膝区物理的重要手段,而宇宙线的成分鉴别和能量重建精度是分成分能谱测量的基础.本文通过CORSIKA 软件模拟了不同原初成分的膝区宇宙线的广延大气簇射,对不同次级成分(包括正负电子、伽马射线、缪子、中子和切伦科夫光子)的宇宙线能量重建精度和鉴别能力进行了研究.结果表明: 在膝区能段使用次级粒子中的电磁粒子(电子、伽马射线和切伦科夫光)进行能量重建精度较好,其中对于质子,能量重建精度约为10%—19%;对于铁核,能量重建精度约为4%—8%.对于原初宇宙线的鉴别能力,缪子粒子数密度在低能段(约100 TeV)和高能段(约10 PeV)的鉴别能力均最好,在低能段正负电子和伽马射线横向分布形状的年龄参数的鉴别能力较好,在高能段中子的粒子数密度的鉴别能力较好.本文还对使用EPOS-LHC 和QGSJet-Ⅱ-04 强相互作用模型模拟的不同次级粒子成分的横向分布差异进行了研究.结果表明正负电子、伽马射线和切伦科夫光在距簇射轴垂直距离大于20 m 的区域内,差异在5%以内,缪子的粒子数在距簇射轴垂直距离大于100 m 的区域内,差异在5%以内,而中子成分的粒子数更依赖于强相互作用模型,两种强相互作用模型的差异大于10%.该研究可为地面膝区能段宇宙线实验的能量重建和成分鉴别时次级成分的选取以及探测器类型的选取提供参考.
1 引言
宇宙线是来自宇宙空间的高能粒子,能谱服从幂律谱,且最高能量达到约1021eV.其能谱最主要的特征是在约1015eV 处,幂律谱的谱指数从–2.7转变为–3.1,称为膝区.宇宙线膝区的起源是宇宙线物理中的一个重要课题[1].膝区反映了银河系宇宙射线源加速粒子能力的极限或银河系对宇宙线束缚能力的极限.不同模型预测了单成分宇宙线膝区能谱的拐折能量(谱指数发生改变处的能量)的不同特征.例如,有的模型预测拐折能量正比于原初粒子的电荷Z[2],有的模型预测拐折能量正比于原初粒子的质量数A[3].宇宙线单成分能谱的测量对研究上述转变具有重要意义.
宇宙线的测量目前有直接测量和间接测量这两种方法.直接测量主要是通过高空气球和空间实验对宇宙线进行测量,如CREAM[4],AMS[5],DAMPE[6−8]等,其优点是可以对原初粒子的电荷进行直接测量,它对不同电荷的宇宙线的鉴别能力好,同时可利用加速器实验的束流对探测器进行标定,绝对能标比较好确定.但因载荷限制,有效探测面积较小,对能谱的测量上限只能达到百TeV左右[9].所以对膝区能段宇宙线的测量主要依赖地面实验的间接测量,如KASCADE[10],ARGO-YBJ[11],LHAASO[12],ICECUBE[13],TALE[14],TUNKA[1]
和AS-γ[15]等实验.地面实验通过测量宇宙线在广延大气簇射(extensive air shower,EAS)中产生的次级成分来测量原初宇宙线.相较于直接测量方法,其具有有效探测面积大的优点,可以对膝区的宇宙线的能谱进行测量.但由于不直接测量原初宇宙线粒子,对宇宙线的成分鉴别能力不高,而且能量重建的方法往往依赖于原初粒子的成分和绝对能标不好确定,所以对于地面实验,能量测量和原初宇宙线的成分鉴别能力是进行单成分能谱精确测量的制约因素.
目前大多数实验只对次级粒子中的一种或几种进行测量,例如KASCADE/KASCADE-Grand实验探测能段约为100 TeV—100 PeV,可探测次级粒子中电子、缪子和强子成分[10],通过电磁粒子数和缪子数对膝区宇宙线的质子、氦核、碳、硅和铁元素进行鉴别和能谱测量[16,17];ARGO-YBJ 和LHAASO-WFCTA 样机探测次级粒子中的带电粒子和切伦科夫光子,测量了能量在1 TeV—10 PeV范围内的宇宙线全粒子能谱和轻成分能谱[18].ICETOP/ICECUBE 的测量能段约为250 TeV—1 EeV[19,20],Aartsen 等[20]利用深度学习技术,使用次级粒子在冰中产生的切伦科夫光子对宇宙线能量和成分进行重建,进而实现分成分的能谱测量.这些实验测量不同种类的次级成分,能谱的测量结果也并不相符[16−20].本文将对这些次级成分的能量重建精度和粒子鉴别能力,以及它们的强相互作用模型的依赖进行研究.为理解不同实验测量结果的差别以及如何得到更好的能量重建精度和粒子鉴别能力提供参考.
在EAS 纵向发展达到极大处的海拔高度进行测量,次级粒子的涨落更小,可以得到更好的探测性能,很多实验也在该海拔处对宇宙线进行测量.本文将在膝区能段,对垂直入射的宇宙线在海拔4400 m 处的次级粒子和切伦科夫光子进行研究.第2 节介绍模拟的参数设置,包括探测平面选取,次级粒子和切伦科夫光的参数设置;第3 节研究EAS 中次级成分的横向分布特征和不同强相互作用模型的差异;第4 节研究次级成分对原初宇宙线的能量重建精度;第5 节研究次级成分对原初宇宙线的成分鉴别能力;第6 节是总结.
2 EAS 模拟
本文使用CORSIKA Version-7.7410 版本软件包[21]模拟宇宙线在大气中的EAS,高能强相互作用模型分别采用EPOS-LHC 和QGSJet-Ⅱ-04,具体采用EPOS-LHC 强相互作用模型所得的结果,但将这两种高能强相互作用模型进行了对比(图7 和图8).低能强相互作用模型采用FLUKA,电磁相互作用模型采用EGS4,五种原初成分分别为质子(proton)、氦核(helium)、碳氮氧(CNO)、镁铝硅(MgAlSi)和铁(iron),碳氮氧和镁铝硅的质量数分别为14 和27.原初粒子能量log10(E/GeV)固定为5.1,5.3,5.5,5.7,5.9,6.1,6.5 和6.9.天顶角固定为0°,方位角在0°—360°内均匀投点.为了研究非垂直入射情况下的影响,本文对天顶角固定为45°的事例进行了模拟,并对垂直入射和天顶角45°的结果进行了对比(图17),其余结果均为垂直入射.观测平面选4400 m 的海拔高度,观测平面处地球磁场水平分量为 34.618 μT,垂直分量为36.13 μT.
次级粒子的截断动能设为: 强子0.1 GeV,缪子0.1 GeV,电子1 MeV 和伽马射线1 MeV,选取的截断动能低于CORSIKA 手册中的默认值,以存储更多的次级粒子,同时在选定的截断动能以下的次级粒子对总的横向分布的贡献很小.切伦科夫光的波长设为200—1000 nm,切伦科夫光子的采集区域选取与簇射轴垂直距离分别为r=20,50,100,150,200,300 和400 m 的圆形区域,圆的半径为3 m.真实实验中大气对切伦科夫光有吸收和散射作用,包括瑞利散射、气溶胶散射和臭氧吸收等.但它们依赖于具体的模型,本文主要研究理想状态下的探测性能,所以模拟中暂不考虑这些过程.
3 EAS 中的次级成分横向分布
3.1 次级成分种类
EAS 中产生次级成分包括切伦科夫光子(Cherenkov)、正负电子(electron)、伽马射线(Gamma)、缪子(muon)、中子(neutron)等粒子.图1 是能量log10(E/GeV)=5.1 时,原初粒子为质子(黑色)和铁核(红色)的宇宙线在EAS 过程中产生的次级成分种类和粒子数.其他原初宇宙线在EAS 中产生的次级成分与之类似,在此不再赘述.可以看到,在所设置的观测平面,次级成分中按数量降序排列且较多的次级粒子分别是切伦科夫光子、伽马射线、正负电子、正负缪子和中子.目前大部分实验也是对这些次级粒子进行测量,本文将只对这些次级成分进行研究.

图1 能量为log10(E/GeV)=5.1,原初粒子为质子(黑色)和铁核(红色)在EAS 中次级成分的种类和个数Fig.1.Type and counts of secondary components in the EAS,the primary particles are proton (black) and iron(red).Energy of the primary particle is log10(E/GeV)=5.1.
3.2 次级粒子的横向分布
在EAS 过程中,距离簇射轴的垂直距离记为r,不同r处的次级粒子数密度随r的变化关系,即为次级粒子的横向分布.图2(a)和图2(b)分别是能量log10(E/GeV)=5.1,成分为质子和能量log10(E/GeV)=6.9,成分为铁核的宇宙线,在EAS中产生的次级成分的横向分布.可以看到在相同r处切伦科夫光子数密度是伽马射线光子数密度的几千倍,伽马射线光子数密度是密度最小的中子粒子数密度的100—1000 倍.以r=100 m,能量log10(E/GeV)=6.9,原初粒子以铁核为例,切伦科夫光子数密度约为 4×105m–2,伽马射线密度约为100 m–2,正负电子数密度约为10 m–2,缪子数密度约为0.3 m–2,中子数密度约为0.05 m–2.
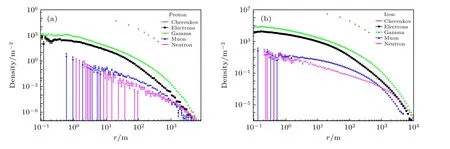
图2 不同原初粒子 在EAS 过程中产生的次级成分的横向分布 (a) 能量log10(E/GeV)=5.1,原初粒子为质子;(b) 能量log10(E/GeV)=6.9,原初粒子为铁核Fig.2.Lateral distribution of secondary components produced by different primary particles during EAS: (a) Primary particle is proton with energy log10(E/GeV)=5.1;(b) primary particle is iron with energy log10(E/GeV)=6.9.
为了方便查看次级粒子在探测平面的分布范围,以芯位作为圆心,以距离芯位的垂直距离r为半径取环带,对环带内的次级成分的数量进行计数,结果如图3 所示.图3(a)和图3(b)分别是能量log10(E/GeV)=5.1,成分为质子的原初粒子以及能量log10(E/GeV)=6.9,成分为铁核的原初粒子,横坐标是对log10(r) 均匀取环带.可以看到对于不同能量和不同成分的原初宇宙线,次级粒子数先随r增加而增大,达到最大值,再随r增加而减小.正负电子主要分布在10—100 m 内;伽马射线和缪子主要分布在离芯位几十至几百米的范围内;中子主要分布在离芯位1 km 附近;而切伦科夫光子主要分布在离芯位百米附近.
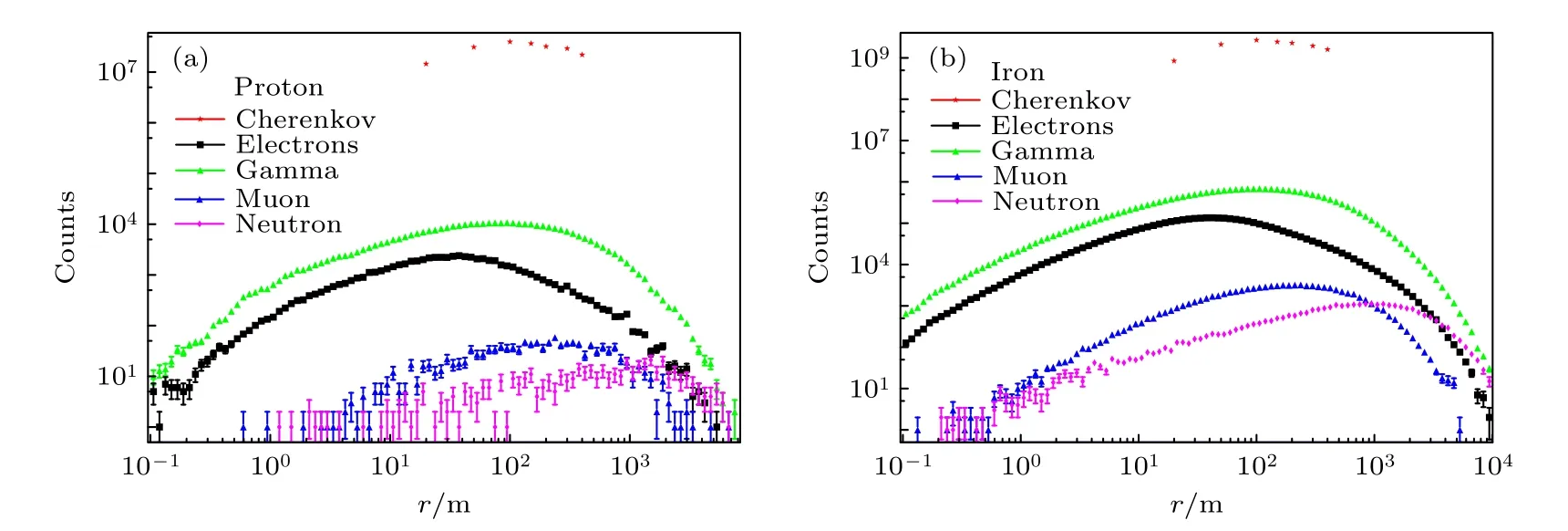
图3 不同原初粒子在EAS 过程中产生的次级成分的数量在探测平面的分布 (a) 能量log10(E/GeV)=5.1,原初粒子为质子;(b) 能量log10(E/GeV)=6.9,原初粒子为铁核Fig.3.Distribution of the number of secondary components produced by different primary particles during EAS in the detection plane: (a) Primary particle is proton with energy log10(E/GeV)=5.1;(b) primary particle is iron with energy log10(E/GeV)=6.9.
对于电磁粒子产生的EAS,通常用Nishimura-Kamata-Greisen (NKG) 函数来描述其次级粒子的横向分布,表达式为

式中,C(s)是关于s的函数,Γ 表示Gamma 函数,r表示距离EAS 簇射轴的垂直距离,ρ1(r)表示r处的粒子数密度,Nsize表示次级粒子总数,RM表示观测平面所在处的摩里尔半径,s表示EAS 发展的年龄[22].
对于原初粒子为质子、氦、氧、硅和铁等粒子的宇宙线,不同地面实验对NKG 函数进行了不同的修正来描述其次级粒子的横向分布.例如,在KASCADE 实验中描述强子在EAS 中产生的次级粒子的横向分布表达式为[23]
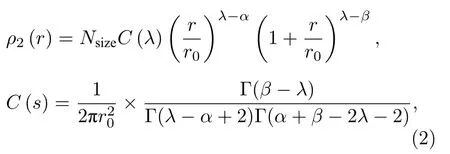
式中,参数λ表示EAS 发展的年龄,是自由参数,而r0,α,β是常数.对于KASCADE 实验,选取α=1.5,β=3.6,r0=40 m.
本文首先尝试使用(2)式对图2 中不同次级成分的横向分布进行拟合.发现对同一横向分布可以存在多组拟合参数,即参数之间存在耦合(例如λ,α,β中只有两个独立).为了减少拟合参数,本文采用一种更为一般的(3)式对次级成分的横向分布进行拟合:

式中,∆是参数.当(3)式中∆=−4.5,r0=RM时,与(1)式一致;当s=λ+0.5,∆=−4.1,r0=40 m时,与(2)式一致.(3)式为双幂律函数,参数具体意义是s表征图3 中粒子数随r增加而增加阶段的幂律指数(或斜率),相当于(1)式中的年龄参数,2s+∆表征图3 中粒子数随r增加而减小阶段的幂律指数(或斜率),r0表征上述两个不同的幂律指数发生改变处的r坐标.

对于次级粒子中的中子,由于次级粒子的数量少,对横向分布函数的限定更弱,每个参数的变化范围更大.参考文献[24]中的(3)式,对本文(3)式某些参数取固定值,并在此基础上对参数进行了优化,发现(7)式可以对中子的横向分布很好地拟合,其中自由参数为和
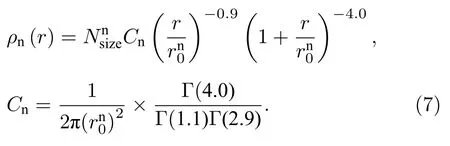
用(3)式和(7)式,对不同成分的宇宙线在EAS 中产生的次级粒子的横向分布进行拟合,如图5 所示.由于模拟中只保存了几个r处的切伦科夫光子,故未对切伦科夫光子的横向分布进行拟合.
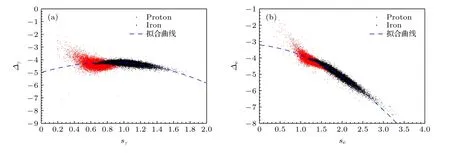
图4 次级粒子中伽马射线(a)和电子(b)的拟合参数 s,∆ 的相关性 (原初粒子为质子和铁核,蓝色虚线为拟合曲线)Fig.4.Dependence between parameters sand ∆ in gamma (a) and electron (b) lateral distribution fitting (Shower is induced by proton and iron respectively,and the blue dotted line is the fitting curve).
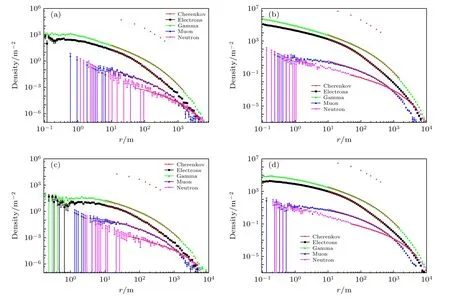
图5 原初粒子在EAS 中产生次级成分的横向分布拟合结果 (a),(b) 原初粒子为质子,能量分别为log10(E/GeV)=5.1 (a),log10(E/GeV)=6.9 (b);(c),(d) 原初粒子为铁核,能量分别为log10(E/GeV)=5.1 (c),log10(E/GeV)=6.9 (d).绿色、黑色、蓝色、粉色点分别表示次级粒子中伽马射线、电子、缪子和中子,最上端的红色五角星表示切伦科夫光,对应颜色的实线为拟合曲线Fig.5.Fitting of lateral distribution of secondary components: (a),(b) Primary particle is proton with log10(E/GeV)=5.1 (a) and log10(E/GeV)=6.9 (b);(c),(d) primary particle is iron with log10(E/GeV)=5.1 (c) and log10(E/GeV)=6.9 (d).The green,black,blue,and pink points represent gamma,electron,muon,and neutron respectively,the red stars at the top represent Cherenkov light.The solid lines with the same color are the fitted function.
为了检验不同次级成分横向分布的拟合质量,不同成分和能量的宇宙线在EAS 中产生的次级粒子个数的统计值N与拟合值Nsize之间的偏差正如图6 所示.当能量log10(E/GeV) >5.5,各种粒子的偏差均在6%以内,之后将用Nsize的涨落来表征能量重建的精度.
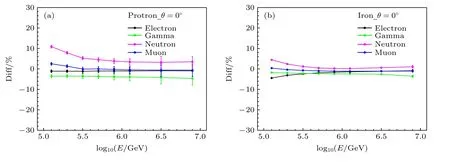
图6 原初粒子分别为质子(a)和铁核(b)在EAS 中产生的不同次级粒子个数的统计值N 与拟合值 Nsize 之间的偏差,Fig.6.Deviation between counted value N and fitted value Nsize for different secondary particles.Shower is induced by proton (a)and iron (b).

图7 EPOS-LHC 强相互作用模型和QGSJet-Ⅱ-04 模型模拟的各种次级粒子横向分布的差异百分比,其中原初粒子为不同能量的质子 (a) log10(E/GeV)=5.1;(b) log10(E/GeV)=6.9Fig.7.Difference in percentage of the lateral distribution of secondary particles between EPOS-LHC and QGSJet-Ⅱ-04 hadronic interaction model,in which the primary particles are protons with different energies: (a) log10(E/GeV)=5.1;(b) log10(E/GeV)=6.9.
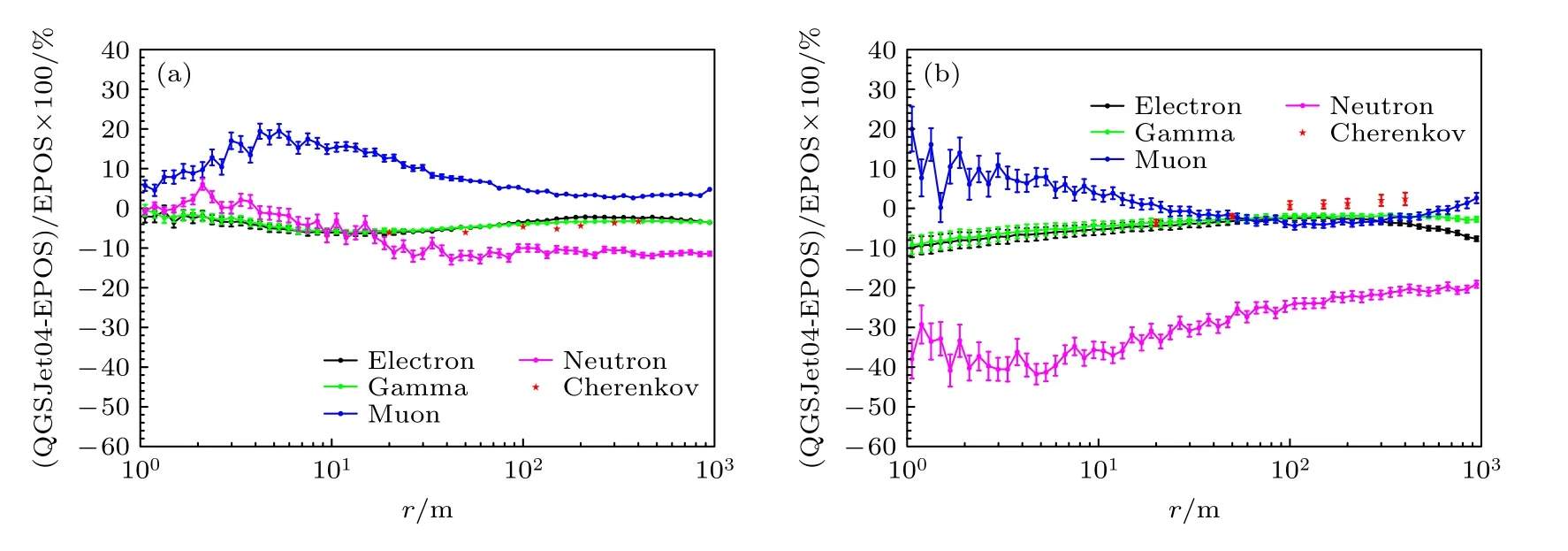
图8 EPOS-LHC 强相互作用模型和QGSJet-Ⅱ-04 模型模拟的各种次级粒子横向分布的差异百分比,其中原初粒子为不同能量的铁核 (a) log10(E/GeV)=5.1;(b) log10(E/GeV)=6.9Fig.8.Difference in percentage of the lateral distribution of secondary particles between EPOS-LHC and QGSJet-Ⅱ-04 hadronic interaction model,in which the primary particles are irons with different energies: (a) log10(E/GeV)=5.1;(b) log10(E/GeV)=6.9.
3.3 不同强相互作用模型的差异
KASCADE 实验中使用不同强相互作用模型测量的膝区质子能谱的流强相差接近一倍[10].本文研究了EPOS-LHC 和QGSJet-Ⅱ-04 两种强相互作用模型横向分布的差异,结果如图7 和图8 所示.可以看到正负电子、伽马射线和切伦科夫光子在两种模型中数量的差异很接近,且最小.在r >20m 时,上述三种粒子的模型差异均在5%以内,所有r范围内差异是在10%以内;当r >100 m时,缪子的模型差异在5%以内,但r <100 m 时,最大差异可以接近20% (对应于原初粒子是铁,能量约10 PeV,r在5 m 附近);中子的差异最大,当r >100m 时差异在10%—20%,当r <100 m 时,最大差异约40% (对应于r <10 m).总体来说,当r >100m 时,缪子和中子的模型差异会显著减小.对于测量缪子和中子的实验,建议探测器尺寸大于100 m,并选取大于100 m 处的粒子来进行重建,以减小模型依赖.缪子和中子是强相互作用过程的产物,EPOS-LHC 模型考虑了其他强相互作用模型中没有考虑到的影响,在EPOS-LHC 多重散射下,计算各自的截面时考虑了单个散射的能量尺度,而在基于Gribov-Regge 理论的QGSJet-Ⅱ-04模型中则不是这样[25].文献[25−27]详细研究了不同强相互作用模型的差异,本文在此不做赘述.
4 能量重建精度
分别对宇宙线EAS 产生的次级粒子的横向分布进行拟合,可以得到每种次级粒子的拟合参数.粒子的数量或在某个半径处的粒子数密度通常被用来进行能量重建,而不同次级粒子数量的比例和横向分布的形状参数通常被用来进行原初粒子的成分鉴别.本文将使用第3 节拟合得到的四种次级粒子的Nsize和统计得到的不同r处的切伦科夫光子数来表征能量重建精度,并比较它们之间的差异.本文只研究固定成分下的能量重建精度,对于能量重建的成分依赖问题,以及真实观测数据结合成分敏感变量构造成分无关的能量重建变量,超出本文研究范围,不做研究.本文的结果会优于考虑成分修正后的结果,所以可认为是使用单一次级粒子进行能量重建的上限.
由于原初粒子的能量正比于次级粒子的数量或粒子数密度,

所以次级粒子数量或粒子数密度的展宽百分比(定义为数量或数密度分布的展宽除以分布的均值)等于重建能量的分辨率,
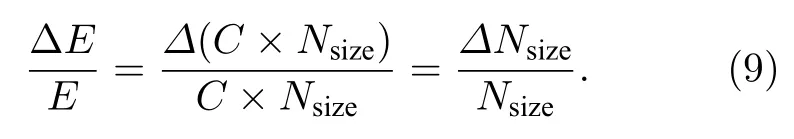
由于模拟过程均在几个离散的固定能量处进行,不涉及到能量范围的宽度对粒子数分布展宽的影响.所以本文将直接使用粒子数量或粒子数密度的分布展宽的百分比来表征能量重建精度,而不进行具体的能量重建,展宽的计算采用高斯函数拟合的σ值.
目前最普遍使用的能量重建方法是用某一固定r处的次级粒子数密度ρ(电子数密度为ρe、伽马射线数密度为ργ、缪子数密度为ρμ、中子数密度为ρn)来重建能量[28].图9 为原初成分为铁时,不同能量的原初粒子产生的次级电子的密度ρe的展宽百分比随位置r的变化曲线,不同颜色的线代表原初粒子的不同能量.可以看到对于次级粒子中的电子数密度,其展宽百分比在100—500 m 范围的ρe展宽较小,且对原初粒子的成分和能量依赖较小.对其他次级粒子有类似的性质,不再赘述.伽马射线 在 300—800 m 范围较好,缪子 在 150—600 m范围较好,中子 在 800—2000 m 范围较好.本文将使用200 m 处的电子数密度、500 m 处的伽马射线密度、250 m 处的缪子密度和1000 m 处的中子密度的展宽百分比来表征用它们来进行能量重建的精度(图11).

图9 原初粒子为不同能量的铁核产生的次级电子的粒子数密度的展宽百分比随离簇射轴垂直距离的变化Fig.9.Resolution in percentage (sigma/mean) of the particle number density of secondary electrons varies with perpendicular distance to the shower axis.The secondary electrons are induced by iron with different energies.
另一种减小粒子数分布的展宽的方法是使用年龄参数s对粒子数进行修正[29].由于在观测平面的次级粒子数受EAS 发展阶段的影响,而年龄参数s表征EAS 在观测平面的发展阶段,使用年龄参数修正Nsize可减小EAS 发展阶段对它的影响.图10(a)是原初粒子能量log10(E/GeV)=5.1,成分为铁时,次级电子的拟合参数Nsize随se的分布,其中 ln()随着se增加而减小,红色实线为直线拟合,将 ln()按红色实线修正到se的均值处,记为 ln() ,能有效地减小Nsize的展宽.图10(b)中红色和蓝色曲线分别表示修正前后的分布,并用高斯函数进行拟合.修正后 ln() 的展宽明显更小,可用它来表征这种方法的能量重建精度,结果如图11 所示.图11 展示了原初粒子为铁时,分别使用年龄修正前后的Nsize,Nsize2和次级粒子数密度ρ进行能量重建的能量重建精度的对比,以及能量重建精度随原初粒子能量的变化关系.可以看到对于次级粒子中的电子和伽马射线,使用年龄参数修正后的粒子数,以及粒子数密度相对于直接使用粒子数能有效地提高能量重建精度,且年龄参数修正的粒子数的能量重建精度略好于粒子数密度得到的能量重建精度,但相差不大.对于次级粒子中的缪子和中子,年龄参数修正的粒子数、粒子数密度和粒子数得到的能量重建精度相差不大.由于年龄参数修正的曲线依赖于原初粒子的能量和种类,而粒子数密度选取的半径为固定值,且它们得到的能量重建精度相差不大,所以将使用次级粒子在固定r处的粒子数密度来表征最优的能量重建精度.这里的结果采用EPOS-LHC 模型,QGSJet-Ⅱ-04模型的能量重建精度的结果也类似.本文研究的是理想情况下的极限探测性能,不涉及到探测器响应等过程,这里暂未考虑两种强相互作用模型的粒子数均值差异导致的能量重建系统误差.
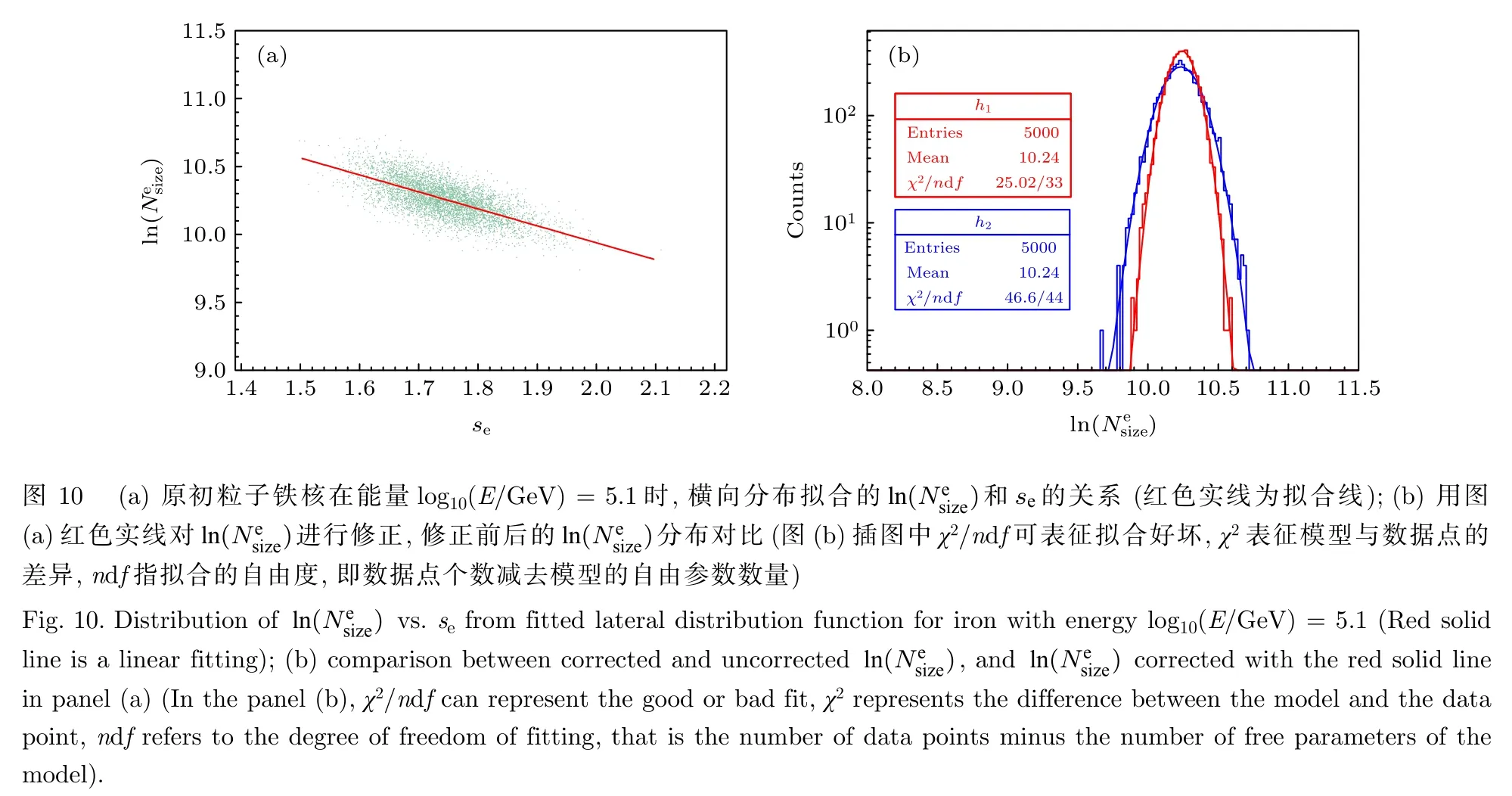

图11 原初成分为铁核,分别用横向分布拟合的 Nsize ,Nsize2和 ρ 进行能量重建的精度.次级粒子分别为电子(a)、伽马(b)、缪子(c)和中子(d); Nsize2表示修正之后的NsizeFig.11.Energy resolution reconstructed by Nsize ,Nsize2 ,and ρ, respectively.Shower is induced by iron.The secondary particles are electron (a),gamma (b),muon (c) and neutron (d),respectively; Nsize2indicates the amended Nsize .
图12 给出了原初粒子为铁时,距离芯位不同垂直距离r处的切伦科夫光子数 (NC)分布的展宽百分比,其中心距簇射轴的垂直距离分别为r=20,50,100,150,200,300 和400 m.可见r=50,150和200 m 处的切伦科夫光子数展宽较小,约为4%—7%.

图12 原初粒子为铁核时,距离芯位不同垂直距离 r 处的切伦科夫光子数 NC 分布的展宽百分比随原初粒子能量的变化关系Fig.12.Resolution in percentage (sigma/mean) of Cherenkov photon number NC varies with the energy of the primary particle at different vertical distance r from the core site.Shower is induced by iron.
不同次级成分得到的能量重建精度如图13 所示,其中图13(a)—(e)的原初粒子分别对应于质子、氦、碳氮氧、镁铝硅和铁.对于质子,次级粒子中电子、伽马射线和50 m 处切伦科夫光子的能量重建精度较好,约为10%—19%;对于铁,次级粒子中伽马射线、150 m 处切伦科夫光子和缪子的能量重建精度较好,约为4%—8%.原初粒子质量数越大,其能量重建精度越高.实验中可以根据不同次级粒子单独能量重建的精度将多种次级粒子结合得到成分依赖更小和精度更高的能量重建变量.上述结果可为能量重建的次级粒子种类的选取,能量重建方法,离芯位距离的选取提供参考意义.

图13 不同次级成分的能量重建精度随原初粒子能量的变化关系,原初粒子分别为质子(a),氦核(b),碳氮氧(c),镁铝硅(d),铁核(e) (彩色线表示不同的次级粒子)Fig.13.Energy resolution from different secondary components vs.primary particle energy.The primary particles are proton (a),helium (b),CNO (c),MgAlSi (d),iron (e) (Colored lines indicate different secondary type).
5 粒子鉴别能力
宇宙线原初粒子的鉴别是宇宙线单成分能谱测量的关键.对EAS 中次级成分的原初粒子敏感性的研究可为成分鉴别变量的选取提供指导.本文将根据第3 节得到的次级粒子横向分布的拟合参数,研究这些参数对原初粒子的鉴别能力.由于切伦科夫光主要根据成像来对原初粒子进行鉴别,超出本文研究范围,不做研究.通过第4 节的研究可以看到粒子数密度相比于粒子总数的涨落更小,用于成分鉴别也会有更好的鉴别能力,这里将使用粒子数密度ρ代替粒子总数Nsize来研究粒子鉴别能力.
本文将在相同能量的条件下来研究各个变量的成分鉴别能力,这可以展示每个变量独立的鉴别能力.对于真实实验数据,可以结合能量重建变量构造和能量无关的成分鉴别变量.比如次级粒子的电磁粒子数和缪子数,它们均和原初粒子能量和种类相关,电磁粒子的涨落更小,缪子数对成分更加敏感,则可以以电磁粒子为基础,使用缪子数对它进行修正得到与成分无关的能量重建变量,以缪子数为基础,使用前面的能量重建变量对它进行修正得到能量无关的成分敏感变量.由于篇幅原因,这里不做赘述.
图14 是次级粒子分别为正负电子、伽马射线、缪子和中子时,研究粒子数密度ρ和年龄参数s对质子和铁核的鉴别能力.图14 不同颜色的点分别表示能量为log10(E/GeV)=5.1,log10(E/GeV)=6.1 和log10(E/GeV)=6.9 的质子和铁核.可以看到,正负电子和伽马射线的年龄参数s,缪子和中子的粒子数密度的成分鉴别能力较好.为了更形象地展示它们的粒子鉴别能力,将相同能量下的质子和铁核的分布分别投射到上述变量的坐标轴上,结果如图15 和图16 所示.可以看到缪子粒子数密度ρμ在低能和高能段的鉴别能量均最好,在低能段(如100 TeV 附近)正负电子和伽马射线横向分布形状的年龄参数se,sΓ的鉴别能力较好,在高能段(如10 PeV 附近)中子的粒子数密度ρn的鉴别能力较好.实验中可以根据不同次级粒子单独进行粒子鉴别的鉴别能力将多种次级粒子结合得到能量依赖更小和鉴别能力更好的成分鉴别变量.这可为不同能量下的成分鉴别变量和探测器类型的选取提供参考.
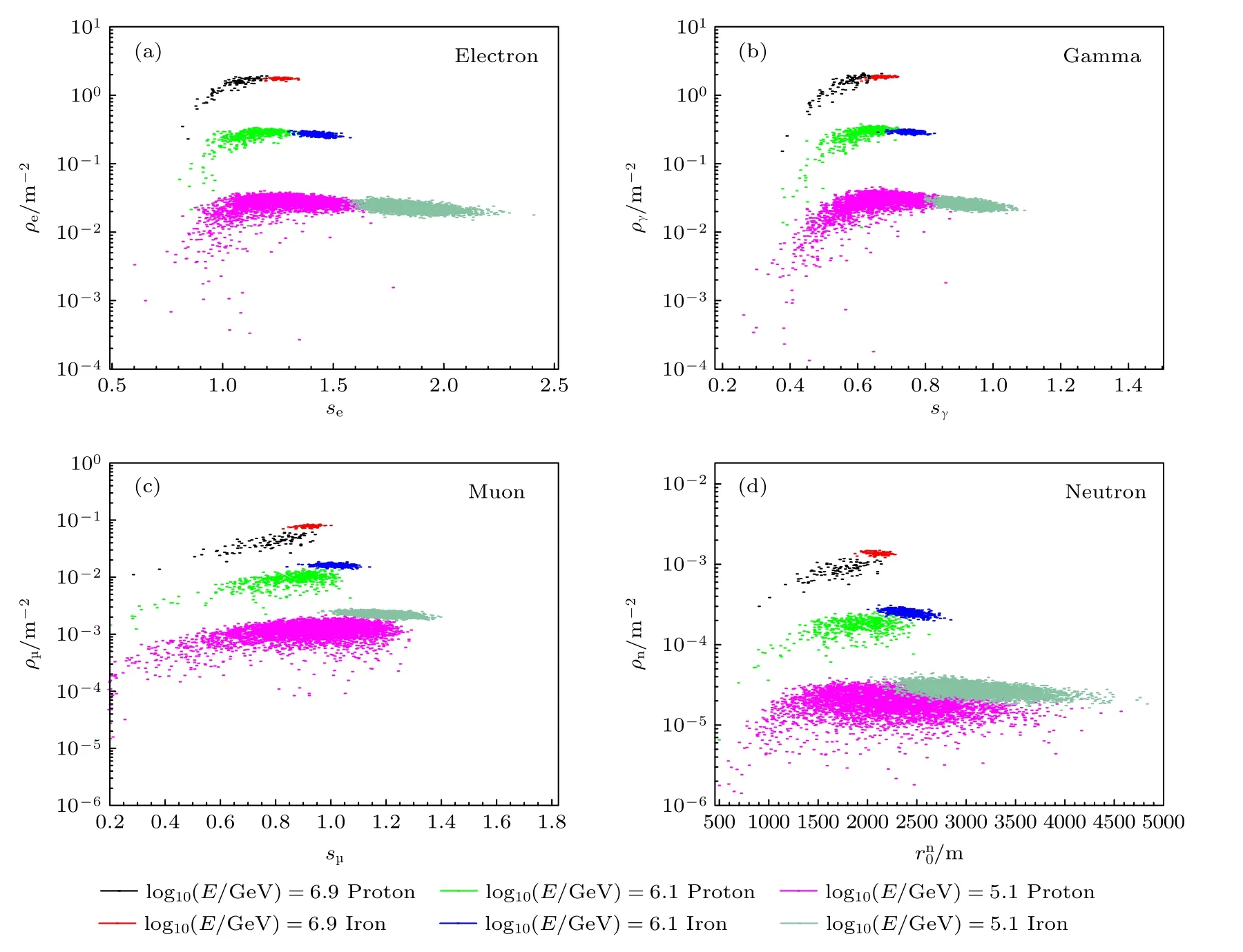
图14 对于不同的能量的原初粒子质子和铁核,ρ 和s 的关系 (a) ρe vs. se;(b) ργ vs. sγ;(c) ρμ vs. sμ;(d)ρn vs. Fig.14.Distribution of ρ vs.s when shower is induced by proton and iron respectively with different energies: (a) ρe vs. se ;(b) ργ vs. sγ;(c) ρμ vs. sμ;(d) ρn vs. .

图15 原初粒子为质子和铁核的参数 (a) se,(b) sγ ,(c) ρμ,(d) ρn 分布的对比(原初粒子能量均为log10(E/GeV)=5.1)Fig.15.Comparison of the distribution of (a) se ,(b) sγ ,(c) ρμ,(d) ρn between proton and iron with log10(E/GeV)=5.1.
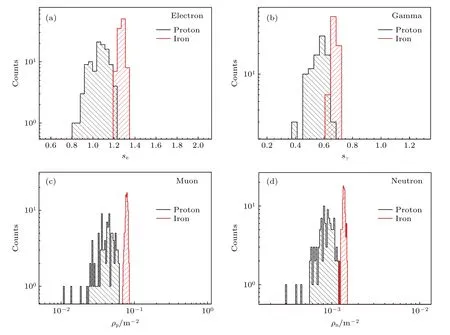
图16 原初粒子为质子和铁核的参数 (a) se,(b) sγ ,(c) ρμ,(d) ρn 分布的对比(原初粒子能量均为log10(E/GeV)=6.9Fig.16.Comparison of the distribution of (a) se,(b) sγ ,(c) ρμ ,(d) ρn between proton and iron with log10(E/GeV)=6.9.
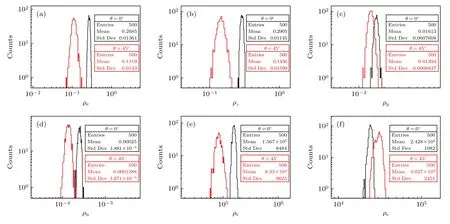
图17 原初粒子铁核能量log10(E/GeV)=6.1 时,垂直入射(θ=0°)和天顶角为45° (θ=45°)时次级成分中 ρe(a),sγ(b),ρμ (c),ρn(d),以及 r=50 m(e),r=150 m (f)处ρC 的分布对比Fig.17.Comparison of the distribution of ρe(a),sγ(b),ρμ(c),ρn(d) and ρCat r=50 m (e),r=150 m (f) for θ=0° and θ=45°.The primary particle is iron with energy log10(E/GeV)=6.1.
本文也研究了天顶角为45°的情况,对比垂直入射情况,将增加大气深度.对于本文研究的能段和选取的海拔高度,天顶角为45°的大气深度将超过簇射发展到极大处所需的大气深度,而垂直入射的大气深度在簇射发展到极大处附近,所以探测到的次级成分的分布将受到影响,进而影响能量重建精度和粒子鉴别能力,不同天顶角的次级成分的分布对比如图17 所示.可以看到,随着天顶角的增加,电子和伽马射线由于已经经过了簇射极大处,粒子数将减少,而且自身的涨落也显著变大.而缪子在传播过程中与大气相互作用少,大气深度的增加对缪子数的影响很小,缪子数的涨落变化也很小.中子由于还继续与大气发生强子簇射过程,相对于缪子衰减更多,中子的涨落随天顶级的增加而增加,幅度处于电磁粒子和缪子之间.望远镜在固定位置处测量切伦科夫光,切伦科夫光的密度ρC随天顶角的变化依赖探测区域距离簇射轴的垂直距离r.如图17 所示,在r=50 m 处,切伦科夫光子数随天顶角的增加而减小,而在r=150 m 处,切伦科夫光子数随天顶角的增加而增加.而且在r=50 m和r=150 m 处切伦科夫光子数的涨落均显著变大,变化幅度和电磁粒子的涨落幅度变化相当.总而言之,当大气深度超过簇射发展极大处的大气深度时,各种次级成分的涨落均增大,缪子的涨落变化最小,电磁粒子的涨落变化最大.
6 总结
宇宙线膝区单成分能谱是理解宇宙线膝区物理起源的重要手段,目前只有地面实验可对这一能段的单成分能谱进行测量.由于地面实验缺乏好的绝对能量定标方法,以及只能对原初粒子在EAS中产生的次级粒子进行测量,不能直接对原初粒子进行测量,地面实验的能量测量和粒子鉴别能力称为单成分能谱测量的限制因素.基于此,本文模拟了垂直入射的不同能量和不同原初粒子成分的宇宙线在EAS 中位于海拔4400 m 观测平面处的次级成分特征,次级成分包括正负电子、伽马射线、缪子、中子和切伦科夫光子.详细研究了各种次级成分的横向分布特征,以及不同次级成分横向分布的强相互作用依赖,还使用具体的函数对横向分布进行了很好地拟合.并用这些拟合参数详细研究了它们用于能量重建的方法和精度,强相互作用模型依赖以及用于宇宙线粒子鉴别的鉴别能力.为各种地面实验的探测器类型选取、能量重建方法、成分鉴别变量的选取提供参考意义.
对于能量重建,使用次级粒子在距离芯位垂直距离r为某一数值处的粒子数密度进行能量重建,相对于次级粒子总数是一个更好的选择.相对于年龄参数修正的粒子总数,它的成分依赖更小.原初粒子为质子时,次级粒子中电子、伽马射线和50 m 处切伦科夫光子的能量重建精度较好,约为10%—19%;原初粒子为铁时,次级粒子中伽马射线、150 m 处切伦科夫光子和缪子的能量重建精度较好,约为4%—8%.原初粒子质量数越大,其能量重建精度越高.实验中可以根据不同次级粒子单独能量重建的精度将多种次级粒子结合得到成分依赖更小和精度更高的能量重建变量.
对于粒子鉴别,缪子粒子数密度ρμ在低能段和高能段的鉴别能量均最好,在低能段 (如100 TeV附近) 正负电子和伽马射线横向分布形状的年龄参数se,sγ的鉴别能力较好,在高能段 (如10 PeV附近) 中子的粒子数密度ρn的鉴别能力较好.实验中可以根据不同次级粒子单独进行粒子鉴别的鉴别能力将多种次级粒子结合得到能量依赖更小和鉴别能力更好的成分鉴别变量,例如多变量分析的方法[30]或深度学习的方法[31].本文所提供的参数可以直接作为训练变量.
对于EPOS-LHC 和QGSJet-Ⅱ-04 两种强相互作用模型导致的次级粒子横向分布的差异,正负电子、伽马射线、切伦科夫光子的数量差异很接近,且比缪子和中子小,在r >20 m 时,均在5%以内,在所有r范围内在10%以内;缪子的数量差异在r >100 m时在5%以内,但在r <100 m 内,最大差异可以接近20% (对应于原初粒子是铁,能量约10 PeV,r在5 m 附近);中子的差异最大,在r >100 m时差异在10%—20%,在r <100 m 时,最大差异约40% (对应于r <10 m).总体来说,在r >100 m 时,缪子和中子的模型差异会显著减小.实验中选取大于100 m 处的次级粒子进行重建.能有效地降低强相互作用模型的依赖.
对于天顶角45°入射情况,相对于垂直入射,电磁粒子数将显著减小,且涨落变大,相应地通过它们得到的能量重建精度和粒子鉴别能力也会变差.而缪子的数量将稍微减小,缪子数的涨落变化不大,探测性能受影响小.中子的数量减小和粒子数涨落的增加介于电磁粒子和缪子之间.切伦科夫光子相对于垂直入射的变化依赖于光子与簇射轴的垂直距离,光子数的涨落相对于垂直入射也会变大,涨落变化的幅度和电磁粒子相当.总而言之,当大气深度超过簇射发展极大处的大气深度时,各种次级成分的涨落均增大,探测性能变差.其中缪子的涨落变化最小,电磁粒子的涨落变化最大.
综上所述,本文在不考虑探测器效应的情况下,研究了各种次级成分进行能量重建时的能量重建精度和对原初粒子成分的鉴别能力,为地面实验的探测器类型选取、能量重建变量和方法、成分鉴别变量的选取提供参考.

