温度对CoCrFeMnNi 高熵合金冲击响应和塑性变形机制影响的分子动力学研究*

闻鹏 陶钢

(南京理工大学能源与动力工程学院,南京 210094)

高熵合金作为一类新兴合金材料,由于其优异的力学性能,在航空、航天、军事等领域具有广阔的应用前景.本文利用分子动力学方法,探讨了温度对CoCrFeMnNi 高熵合金冲击响应和塑性变形机制的影响.研究发现,初始温度的增加使得冲击压力、冲击波传播速度和冲击温升下降.冲击Hugoniot 弹性极限随着温度的上升线性下降.随着冲击强度的增加,CoCrFeMnNi 高熵合金发生了复杂的塑性变形,包括位错滑移、相变、变形孪晶和冲击诱导非晶化.在较高的初始温度下,CoCrFeMnNi 高熵合金内部出现无序团簇,其和由面心立方晶体结构转变而成的体心立方晶体结构以及无序结构是位错成核的重要来源.由于Mn 元素具有相对较大的原子体积和势能,所以在Mn 元素的周围会出现较大的晶格畸变和局部应力,从而为冲击诱导塑性变形提供较大的贡献.在温度较高时,Fe 元素对塑性变形的贡献和Mn 元素一样重要.研究结果有助于深刻理解CoCrFeMnNi 高熵合金的冲击诱导塑性和相关变形机制,为CoCrFeMnNi 高熵合金在不同温度下涉及高应变率冲击过程的应用提供理论支撑.

1 引言

高熵合金(high-entropy alloy,HEA)是由五种或五种以上的元素按照等原子比或接近于等原子比(5%到35%)组成的合金.由于其具有较高的熵值,所以被称作高熵合金[1,2].通过调节元素种类及数量、晶粒尺寸和制备工艺,高熵合金可以兼具高强度、低密度、耐腐蚀、耐磨性、超导性和抗辐照等优异性质[3−6],在航空、航天、军事等领域具有广阔的应用前景.

与一种元素作为主要元素的合金相比,高熵合金中各个元素占据晶格格点位置的概率是一样的.而高熵合金中不同元素的原子半径不同,所以在结构上产生了严重的晶格畸变,使得传统晶体和非晶的塑性变形机制并不完全适用于高熵合金.例如在高熵合金中位错并不能沿着特定的滑移面运动,而是根据原子的排列情况在运动过程中调整滑移面,这使得位错之间的相互作用大大增加,从而为高熵合金提供了更多变形的可能,所以高熵合金具有好的均匀变形能力以及高强度的特性.高熵合金复杂的微观结构导致其内部的位错运动难以预测.尤其是在冲击载荷作用下,高熵合金还要面临高温、高压和高应变率等极端变形环境,原有的晶体材料的位错均匀成核机制不再完全适用于高熵合金.

目前对高熵合金变形机制的研究还处于探索阶段[7−9].Zhang 等[5]认为高熵合金的变形机制介于传统合金和非晶合金之间.传统晶态合金的变形机制包括位错的滑移、攀移和变形孪晶等,非晶合金的变形则是通过剪切转变区、拉伸转变区、自由体积和原子应力模型等进行分析[10].需要进一步研究冲击等高动态条件下高熵合金的变形机制模型.

自Jiao 等[11]和Kumar 等[12]发表了有关高熵合金的动态变形机制以来,相关研究被陆续报道.Qiao 等[13]利用分裂式霍普金森杆(split Hopkinson tensile bar)实验揭示了CrMnFeCoNi 高熵合金在冲击拉伸下孪晶和位错的协同作用机制,这使得CrMnFeCoNi 高熵合金同时具有较高的动态强度和塑性.Jiang 等[14]通过平板冲击实验发现面心立方晶体(face-centered cubic,FCC)结构CrMnFe CoNi 高熵合金和体心立方晶体(body-centered cubic,BCC)结构NiCoFeCrAl 高熵合金表现出相对较高的Hugoniot 弹性极限和高相变阈值应力.Liu 等[15]和Chen 等[16]发现WFeNiMo 高熵合金对钢靶的侵彻深度较钨合金有明显提升,这是由于多相结构特别是微米级µ相析出物促进了非均匀变形,使析出物与FCC 基体之间产生了较大的应变梯度.在侵彻过程中,储存的能量表现为与应变梯度相关的高密度位错,驱动动态再结晶软化,导致剪切带的形成和由此产生的侵彻自锐行为.Zhang等[17]发现动态条件下HfZrTiTa 高熵合金表现出热塑性不稳定性,变形局限于绝热剪切带,并受到应变硬化、应变速率强化和热软化的共同影响.Zhang 等[18]发现在动态加载下,由于位错拖拽机制和位错热激活机制的共同作用,双相BCC 结构AlCoCr1.5Fe1.5NiTi0.5高熵合金的屈服强度随着应变速率的增加而增加.上述试验研究为深刻理解高熵合金在高动态条件下的变形机制提供了基础.

作为研究材料微观结构演化的重要手段,分子动力学(molecular dynamics,MD)方法被广泛应用于材料的冲击响应研究.闻鹏等[19]综述了模拟材料冲击的分子动力学方法,主要包括非平衡分子动力学(non-equilibrium MD)和平衡分子动力学(equilibrium MD)两大类.同时总结了利用分子动力学方法可以研究的相关材料冲击问题,如材料的冲击波结构、Hugoniot 弹性极限(HEL)、冲击Hugoniot 关系、冲击诱导相变、冲击诱导熔化、冲击变形图、破坏等.利用分子动力学方法,Zhao 等[20]研究了BCC 结构TiZrNb 和 NiCoFeTi 高熵合金的冲击响应,发现了具有高稳定性的异常扩展刃型位错结构,其可以促进更快的位错运动,从而阻止变形孪晶的早期成核.Xie 等[21]和Jian 等[22]对CoCrNi 中熵合金进行了冲击压缩研究,发现随着冲击强度的上升,CoCrNi 中熵合金的塑性变形机制从位错滑移和孪晶向固态非晶化(amorphization)转变.同时发现由于晶格畸变阻碍了位错的传播,CoCrNi 中熵合金的HEL 表现出异常的各向异性.Thürmer 与Gunkelmann[23]和Thürmer等[24]研究了纳米结构高熵合金的冲击破坏现象,与单晶高熵合金相比,纳米晶高熵合金的破坏强度明显降低,在冲击压缩和释放(release)的过程中存在大量的堆垛层错、孪晶和位错.Liu 等[25]研究了晶体取向对 CoCrFeMnNi 高熵合金冲击塑性的影响,发现Mn 元素在BCC 结构和无序结构中占比相对较高,在CoCrFeMnNi 高熵合金的冲击塑性中起着重要作用.Sandeep 和Parashar[26]研究了晶格畸变和纳米孔洞对CoCrCuFeNi 高熵合金冲击压缩行为的影响,发现晶格畸变有助于降低冲击波传播速度,在较低的温度和冲击速度下,晶格畸变效应更为显着.

材料的变形往往存在很强的温度敏感性,研究发现温度对CoCrFeMnNi 高熵合金的堆垛层错能[27]、拉伸和压缩塑性变形[28,29]、弹性模量以及热膨胀系数[30−32]都有显著影响.随着温度的升高,堆垛层错能逐渐增大,但堆垛层错能相对于温度的斜率略有减小[27].弹性模量随着温度的上升而下降[30−32].在10 到1373 K 温度范围内,通过对CoCr FeMnNi 高熵合金的拉伸和压缩实验发现屈服应力随着温度的上升而下降[29].

材料的应用往往要经受不同温度的考验,而温度也是材料冲击性能的重要外界影响因素.综上所述,温度对高熵合金的动态力学性能影响很大,但是对冲击作用下温度如何影响高熵合金的冲击响应和变形机制并不清楚.本文利用MD 方法,研究了不同初始温度和冲击压力下CoCrFeMnNi 高熵合金的冲击响应和塑性变形,揭示了温度对CoCr FeMnNi 高熵合金的冲击波参量、冲击Hugoniot关系、缺陷结构和变形机制等的影响.为进一步阐明CoCrFeMnNi 高熵合金在高动态冲击作用下的变形机制提供了微观演化基础,同时为CoCrFeMnNi高熵合金在不同温度下涉及高应变率冲击过程的应用提供理论支撑.

2 模型与方法

CoCrFeMnNi 高熵合金原子之间的相互作用通过Choi 等[33]提出的第二近邻修正嵌入原子(2NN MEAM)势函数进行描述,此势函数适用于Co-Cr-Fe-Mn-Ni 多元合金体系的力学性能研究,已经得到固相的混合焓和晶格常数的验证[33],并成功应用于CoCrFeMnNi 高熵合金的压缩和拉伸[34]、纳米压痕[35]和冲击压缩[23−25]的研究.首先将Co,Cr,Fe,Mn 和Ni 元素等比例随机排布,建立 大小 为7.2 nm×7.2 nm×7.2 nm 的FCC 单 晶CoCrFeMnNi 高熵合金模型,用上述小尺寸模型来研究CoCrFeMnNi 高熵合金的结构特征.可以从图1(a)的CoCrFeMnNi 高熵合金模型看到各元素基本上是均匀分布.图2(a)给出了温度对径向分布函数(radial distribution function,RDF)的影响.从1—1000 K,随着温度的升高,CoCrFeMnNi高熵合金的RDF 峰值逐渐下降,宽度变大,同时RDF 峰值所对应的坐标值逐渐增大,说明高温使得原子间距增大,聚集程度下降.当温度为2500 K时,RDF 的第二峰消失,说明此时高熵合金熔化成为液体.如图2(b)所示,随着温度的升高,各元素原子的Voronoi 元胞体积[36](原子体积)逐渐增大,各元素原子体积从大到小排列为Mn,Fe,Cr,Ni,Co.原子体积越大,其引起的局部晶格畸变越大,即更容易在冲击压缩下导致更大的局部塑性变形.

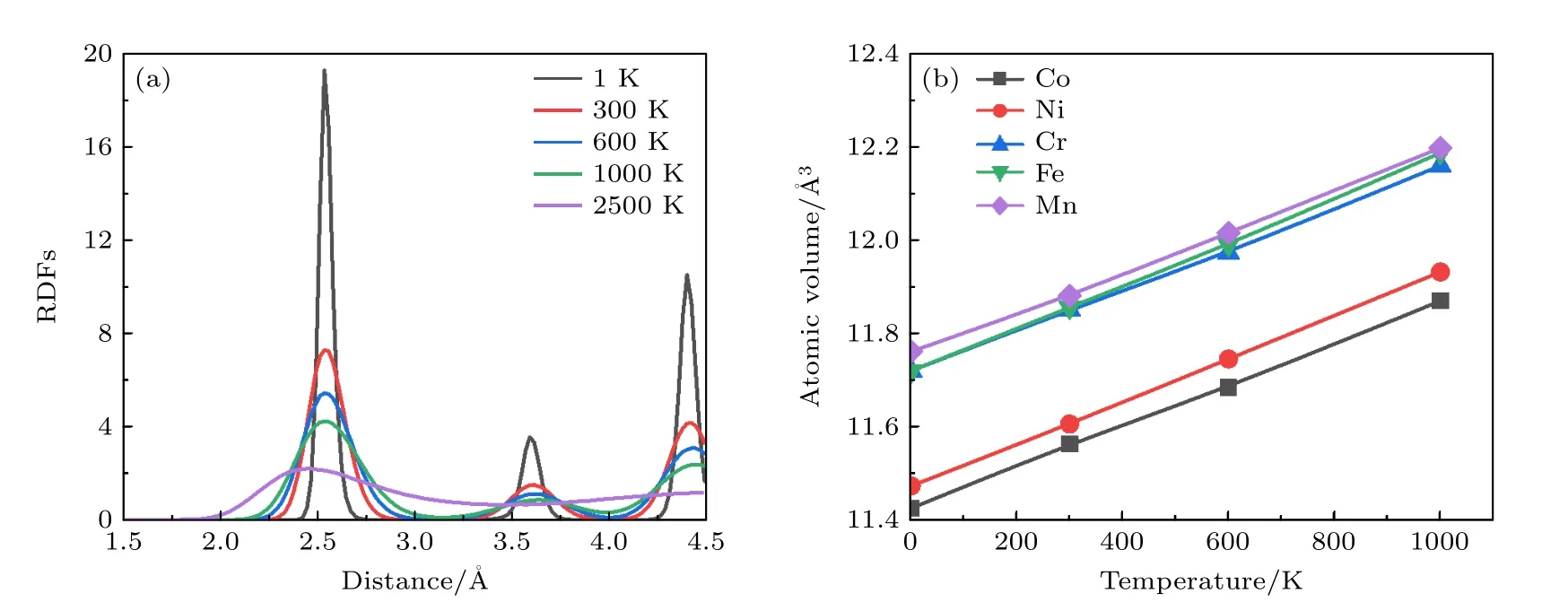
图2 温度对CoCrFeMnNi 高熵合金的影响 (a) 径向分布函数;(b) 原子体积Fig.2.Effect of temperature on (a) RDFs and (b) atomic volume of CoCrFeMnNi HEA.

单晶CoCrFeMnNi 高熵合金的冲击压缩过程见图1(b).初始样品包含1920000 个原子,x,y和z方向的晶体取向分别为[100],[010]和[001].冲击方向(z方向)的长度为108 nm,与其垂直的方向(x和y方向)的长度为14.4 nm.为保证模型内各元素均匀分布,用于冲击的模型包含60 个7.2 nm×7.2 nm×7.2 nm 的小模型,每个小模型都使用不同的随机数随机分配各元素原子.建立模型后,首先对初始单晶CoCrFeMnNi 高熵合金进行平衡处理获得能量最小状态.为了研究初始温度对冲击响应的影响,在等温等压系综(NPT)下分别将模型平衡至1,300,600 和1000 K.使用活塞法[37]在模型中产生冲击波,选择z方向左端面处的薄层(2 nm)作为活塞.初始时刻给定活塞原子沿z方向的速度为Up,同时与其垂直的方向速度为0.冲击波在CoCrFeMnNi 高熵合金内产生后沿z方向向右传播,导致在冲击波前沿后面形成位错等缺陷.活塞速度Up的主要研究范围从0.5 到2 km/s.侧表面施加周期性边界条件,冲击波传播方向设置为自由边界.

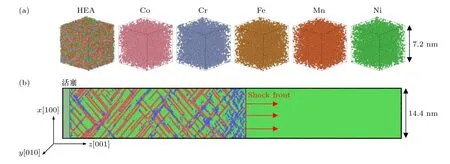
图1 (a) 小尺寸CoCrFeMnNi 高熵合金模型;(b) 大尺寸CoCrFeMnNi 高熵合金冲击压缩过程图Fig.1.CoCrFeMnNi HEA model: (a) Small size;(b) big size for shock compression.

为了分析计算结果,沿冲击波传播方向将样品划分成1 nm 的薄层,每个薄层的输出结果为其中所有原子的平均值.输出信息包括密度ρ、温度T、速度Vz、应力张量Pij和剪切应力Psh.Psh被定义为

温度T通过以下公式计算[38]:

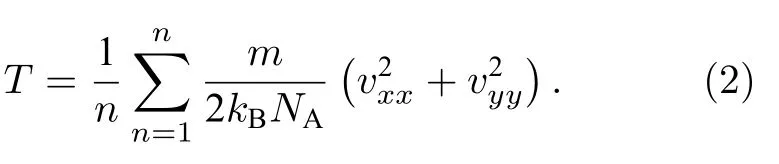
这里没有考虑包含质心平移速度的vzz,m是原子质量,kB是玻尔兹曼常数,NA是阿伏伽德罗数.

MD 模拟使用的是开源程序LAMMPS[39].利用多面体模板匹配(polyhedral template matching,PTM)方法[40]进行结构识别,均方根偏差(root-mean-square deviation)选取为0.1[24].使用OVITO[41]进行后处理及可视化显示.

3 结果与讨论

3.1 温度对冲击参量的影响

首先给出初始温度为1 K、冲击波传播12 ps时,不同冲击强度下冲击压力Pzz和剪切应力Psh在冲击方向上的分布特征,如图3 所示.随着Up的增加,冲击压力Pzz逐渐变大,在相同的时间内冲击波传播了更远的距离.但是压力剖面并未出现明显的弹性波和塑性波分离的现象,所以并不能通过Pzz剖面来确定弹性极限.当Up<1.5 km/s 时,剪切应力Psh随着冲击强度的增加而下降,这是冲击诱导塑性的典型特征.当Up=1.5 km/s时,在冲击波前沿后面Psh下降并出现负值,说明此时Pxx(Pyy) >Pzz,原因是局部发生FCC 到BCC 的结构转变(3.4 节),Thürmer 等[24]也发现了类似的在较强冲击下高熵合金内部剪切应力Psh出现负值的现象.当Up为2.5 和3.0 km/s 时,原子结构发生非晶化(3.4 节),剪切应力转变为正值[22].当Up继续增大到3.5 km/s 时,由于超强的冲击压力(253 GPa),所有原子都呈现流体状态,剪切应力为0.这里把z方向上坐标在40 到 60 nm之间原子的平均剪切应力定义为流动应力Pflow,用以定量分析冲击压缩下的应力状态.

图3 初始温度为1 K 时,不同Up 下沿z 方向上的 (a) Pzz 和(b) PshFig.3.(a) Pzz and (b) Psh along the z-direction for different Up at an initial temperature of 1 K.

图4 给出了Up=1.5 km/s 时,不同初始温度下冲击压力Pzz、剪切应力Psh和温度在z方向上的剖面图.如图4(a)所示,在相同的Up下,初始温度越高,Pzz越小.当初始温度为1 K 时,Pzz=82.2 GPa;而初始温度1000 K 时,Pzz=76.7 GPa,相比于1 K 时下降了6.7%.初始温度越高,冲击波传播的距离越短,即冲击波的速度越小.图4(b)显示随着温度的升高,Psh下降,这是由于较高的初始温度使得高熵合金更容易发生塑性变形,剪切抵抗性下降.当初始温度为1 和300 K 时剪切应力为正值,但是当初始温度上升到600 和1000 K 时,剪切应力已经变为负值.说明随着初始温度的上升,剪切应力出现负值的临界速度也会下降.同时随着初始温度的升高,由冲击引发的温度变化值增加(图4(c)).

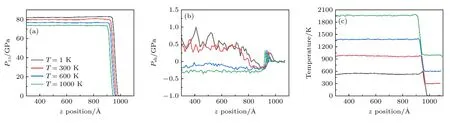
图4 Up=1.5 km/s 时,初始温度对 (a) 冲击压力Pzz、(b) 剪切应力Psh 和 (c) 温度的影响Fig.4.Effects of initial temperature on (a) shock pressure,(b) shear stress and (c) temperature when Up=1.5 km/s.

3.2 温度对冲击Hugoniot 的影响

根据不同时刻冲击波前沿的位置,可计算得到冲击波的传播速度Us.当初始温度为1 K 时,尽管高熵合金模型建立有所不同,但本文得到的Up-Us曲线和Liu 等[25]的计算结果一致,如图5(a)所示.同时,图5(a)也给出了不同初始温度下的Up-Us曲线.和绝大部分的金属材料一样,在塑性阶段,Up和Us存在线性关系,表示为

其中c0和s为拟合参数.通过对塑性区域(0.75 km/s≤Up≤ 2.0 km/s)的Up-Us曲线拟合,得到不同初始温度下的c0和s,见图5(b).随着初始温度的升高,c0逐渐减小.这和其他金属材料的冲击Hugoniot 温度依赖性表现一致[42−45].

当冲击强度大于某一极限时,材料内部会发生塑性变形,这一极限被称为Hugoniot 弹性极限(HEL).由于CoCrFeMnNi 高熵合金沿[001]方向的冲击并未出现明显的弹塑性波分离的现象(图3(a)和图4(a)),所以本文通过流动应力的变化,以及体系内出现位错(3.3 节)为依据确定HEL.图6(a)给出了流动应力Pflow随冲击压力Pzz的变化图.在弹性阶段,Pflow随Pzz的增加有小幅度的上升,随后在HEL 时达到最大值.进入塑性阶段后,Pflow随Pzz的增加迅速下降.图6(b)显示HEL处的Pzz值(PHEL)随着温度的上升而近似线性下降.图7 给出了冲击压缩后体系温度随Pzz的变化,根据HEL 以及不同温度下的冲击压力可以得到弹性和塑性的分界线,在弹性阶段温度上升相对较小,而在塑性阶段体系内会有明显的温度升高,而且初始温度越高,冲击温升越大.

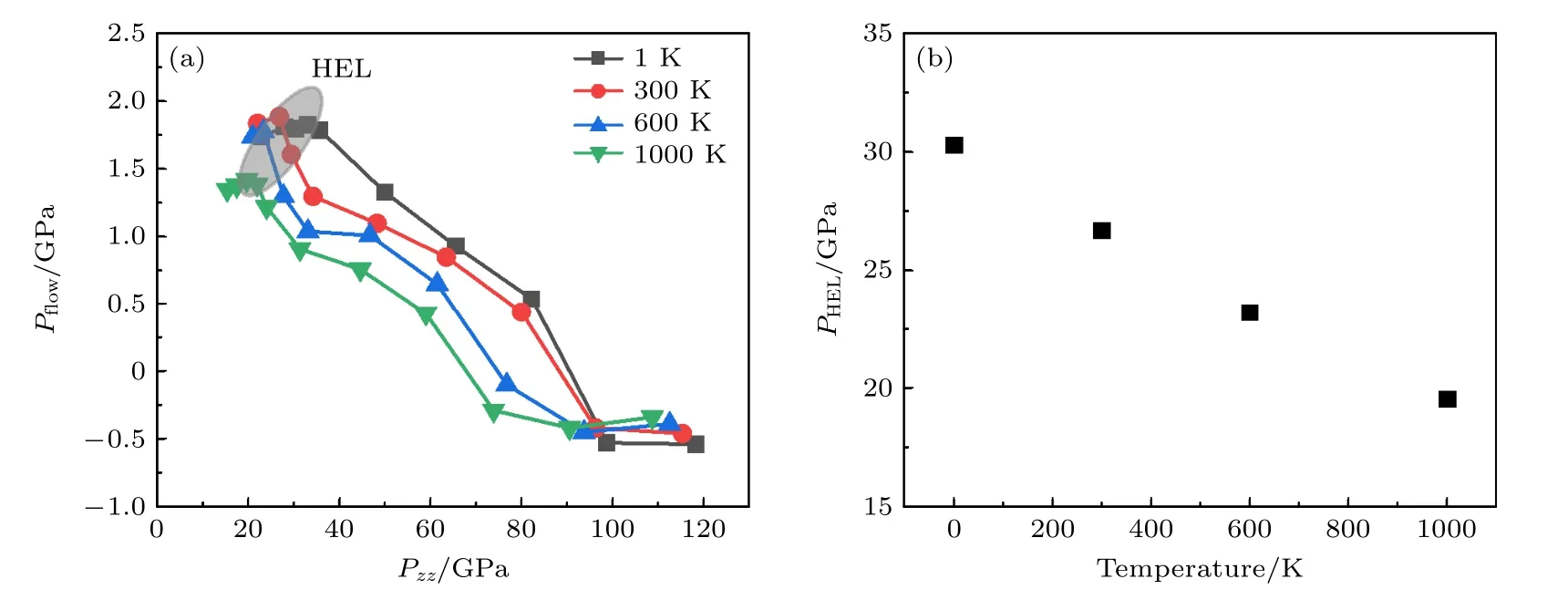
图6 (a) 流动应力Pflow 随冲击压力Pzz 的变化;(b) PHEL 随温度的变化Fig.6.(a) Flow stress Pflow as a function of shock pressure Pzz;(b) PHEL as a function of temperature.

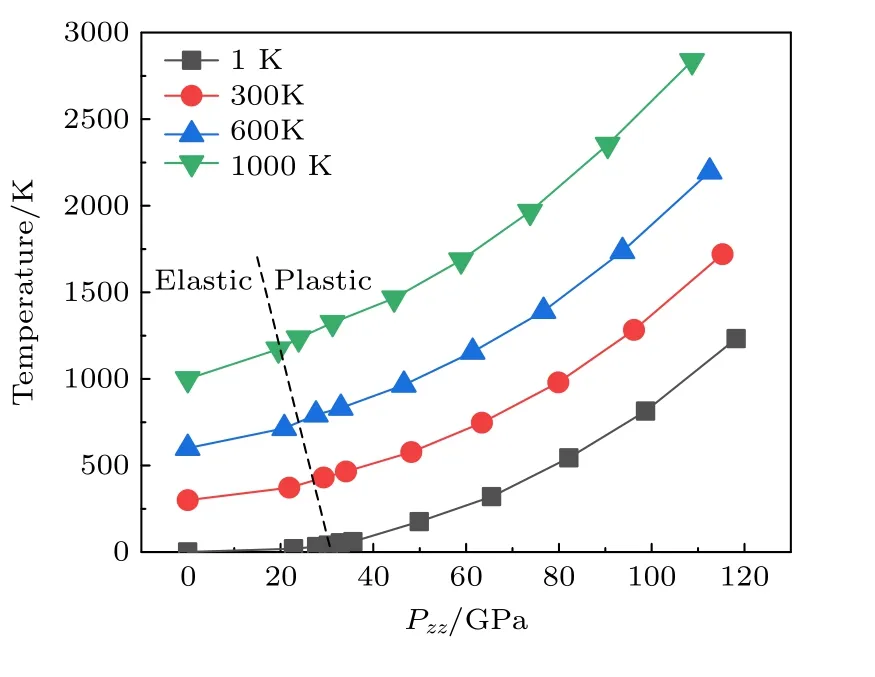
图7 不同初始温度下的冲击温升曲线Fig.7.Shock-induced temperature rise at different initial temperatures.

3.3 温度对CoCrFeMnNi 高熵合金缺陷结构的影响

本节主要对冲击诱导产生的缺陷形态进行分析,具体演化过程和变形机制在3.4 节详细讨论.图8 给出了冲击波传播14 ps,典型Up时不同初始温度下冲击压缩后缺陷结构,不同结构通过PTM 方法[40]进行识别.首先值得注意的是,在未受到冲击压缩的区域,尽管元素的原子大小不同会导致局部的晶格畸变,但是初始温度为1,300 和600 K 的样品仍然是完美的FCC 晶格结构.当初始温度为1000 K 时,样品内部出现了无序结构的白色团簇,这些无序结构里面Mn 原子占比最高,达到25.4%.当Up=0.65 km/s 时,在初始温度为1 K 的样品中只出现少许的BCC 结构团簇,说明此时冲击强度不是很大,样品内部只发生了弹性变形;当初始温度上升到300 K 时,样品内部出现了明显的位错滑移现象,在冲击波经过的地方出现交叉网状结构的堆垛层错(stacking fault,SF),冲击波前沿后面是12 nm 厚的弹性区域,说明此时弹性波传播速度大于塑性波传播速度;随着初始温度上升到600 和1000 K,SF 的密度明显上升.当Up=1.0 km/s 时,缺陷结构还是以SF 为主,相对Up=0.65 km/s 时SF 的密度显著上升,同时弹性区域的厚度也相对减小,说明塑性波在逐渐追赶上弹性波.当Up=1.5 km/s 时,对于初始温度为1 和300 K 的样品,较强的冲击压缩导致冲击波前沿后面区域出现大量FCC 到BCC 的结构转变,这些BCC 结构作为位错成核源导致大量的位错滑移,从而产生SF 和变形孪晶(deformation twinning,DT)(具体演化过程见图13).而当初始温度为600 和1000 K 时,样品内部已经非晶化(3.4 节).

为了定量分析温度对缺陷结构的影响,图9 给出了z方向40—60 nm 区域内(约420 000 个原子)不同结构含量随时间的演化.和图8 相对应,当Up=0.65 km/s 时,初始温度为1 K 的样品内部各结构含量几乎没有变化,只是BCC 结构有1.6%的增加,FCC 结构相应地有1.6%的下降;而对于初始温度为1000 K 的样品,冲击波在6 ps 时达到所选择区域,引起结构含量的剧烈变化,随后在14 ps 时各结构含量趋于稳定,FCC 结构含量从93.7%下降到了58%,相应的HCP 结构和无序结构含量上升到了21.7%和19.4%.当Up=1.0 km/s时,由于冲击压缩的作用,初始温度为1 和1000 K的样品FCC 结构含量分别下降到了53%和35%,相应的HCP 结构和无序结构含量上升.此时较高的温度不仅会带来较多的FCC 到HCP(和无序结构)的转变,同时高温使得局部原子结构非晶化,形成大量的无序结构(图8).当Up=1.5 km/s 时,初始温度为1 K 的样品FCC 结构含量下降到了13.5%,HCP 含量高达77.8%,这对应了图8 中出现的大量DT;而初始温度为1000 K 时FCC 结构含量几乎减小到0,无序结构和BCC 结构的含量分别为67.9%和29.4%.

图8 典型Up 时不同初始温度下的缺陷结构特征Fig.8.Defect structure characteristics at different initial temperatures for typical Up.

图9 典型Up 时不同初始温度下的结构含量随时间的变化 (a) Up=0.65 km/s,T=1 K;(b) Up=1.0 km/s,T=1 K;(c) Up=1.5 km/s,T=1 K;(d) Up=0.65 km/s,T=1000 K;(e) Up=1.0 km/s,T=1000 K;(f) Up=1.5 km/s,T=1000 KFig.9.Atomic fraction of FCC,BCC,HCP and disordered structures as a function of the shocked time at different initial temperatures for typical Up: (a) Up=0.65 km/s,T=1 K;(b) Up=1.0 km/s,T=1 K;(c) Up=1.5 km/s,T=1 K;(d) Up=0.65 km/s,T=1000 K;(e) Up=1.0 km/s,T=1000 K;(f) Up=1.5 km/s,T=1000 K.

高熵合金由多种元素组成,各元素在冲击塑性变形过程中所起到的作用也存在差异,这里通过不同元素在不同结构中所占比例的演化来定量分析各元素对塑性变形的贡献.如图10 所示,初始温度为1 K 时,Mn 元素在BCC 结构和无序结构中的占比最高,而BCC 结构和无序结构是位错成核源,所以Mn 元素对CoCrFeMnNi 高熵合金冲击诱导塑性变形的贡献最大.这和Liu 等[25]的结论一致,Liu 等给出的原因是Mn 元素具有较大的原子半径,导致Mn 元素比其他元素具有更严重的局部晶格畸变,使得Mn 元素周围具有最大的局部应力.本文通过计算发现Mn 元素具有最大的原子体积(图2(b)),从而定量地给出了更为充分的解释.Mn 元素与其他元素之间的结合强度(即原子之间的势能)也存在特异性.图11 给出了原子对之间势能随原子间距离的变化曲线[33].从图11 可以看到,Mn-Mn,Mn-Fe 和Mn-Cr 原子对的势能平衡点所对应的原子距离相对较大,这和上述Mn 元素的原子体积较大相一致.同时它们也具有较高的平衡势能,即Mn-Mn,Mn-Fe 和Mn-Cr 原子对相对不稳定,在受到外界干扰时更容易偏离其平衡状态,所以在冲击压缩时Mn 元素更容易形成BCC结构和无序结构,成为塑性变形时的位错源.初始温度为1000 K 时,Fe 元素在BCC 结构中占比最高,所以除了Mn 元素,Fe 元素也在塑性变形中起着重要的作用,这和图2(b)中各元素的原子体积大小相一致.综上所述,不同元素在塑性变形和结构演化中起着不同的作用,按贡献从大到小排序依次为: Mn,Fe,Cr,Ni,Co;而且在温度较高时,Fe 元素和Mn 元素对塑性变形的作用一样重要.

图10 Up=1.0 km/s 时,初始温度为 (a) 1 和 (b) 1000 K 时不同元素在不同结构中的占比Fig.10.When Up is 1.0 km/s,proportions of Co,Ni,Cr,Fe and Mn with FCC,BCC,HCP and disordered structures as a function of the shocked time at initial temperatures of (a) 1 and (b) 1000 K.

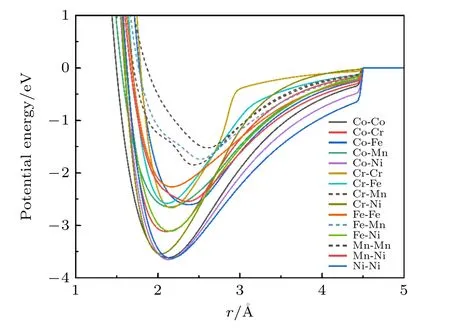
图11 不同原子对之间的势能和原子间距之间的关系[33]Fig.11.Potential energy as a function of interatomic spacing[33].

3.4 冲击压缩下CoCrFeMnNi 高熵合金的变形机制

根据MD 计算结果,图12 给出高熵合金的冲击变形机制,以及温度对变形机制的影响.首先,在冲击强度低于HEL 时,高熵合金内部只发生弹性变形.当冲击强度超过HEL,高熵合金内部发生塑性变形,FCC 结构转变成BCC 结构和无序结构,进而成为位错成核源.元素的异质性也是位错成核的来源,Mn 元素(Fe 元素)由于较大的原子体积和较高的势能,更容易成为位错成核源.位错在冲击波前沿的后面成核,并在〈111〉 平面上滑移扩展,导致HCP 结构的出现,从而在高熵合金内部形成交叉网状的堆垛层错.随着冲击强度的上升,堆垛层错的密度增大,同时在相对较高的冲击压力下出现大量的FCC 到BCC 的相变,同时产生一定数量的变形孪晶.在塑性变形阶段,流动应力会随着冲击强度的增加而下降.当冲击强度足够大时,流动应力下降为0,高熵合金失去剪切抵抗性.

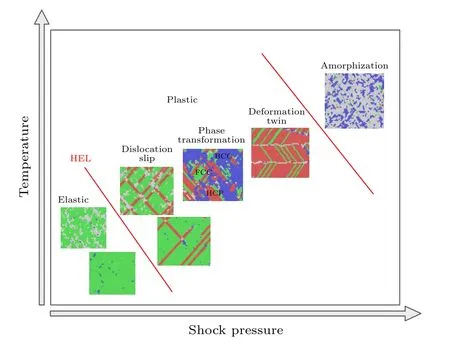
图12 不同冲击压力和温度下,CoCrFeMnNi 高熵合金的变形机制Fig.12.Deformation mechanisms of CoCrFeMnNi HEA under different shock pressures and temperatures.

较高的初始温度使得高熵合金内部存在小尺寸的无序团簇,由于Mn 元素原子体积相对较大,使得Mn 原子周围局部晶格畸变较大,所以无序团簇中Mn 元素占比相对较高,为25.4%.当达到弹性极限时,HEL 随着初始温度的上升而下降,即高温使得高熵合金更容易发生冲击诱导塑性.较高的温度可以降低塑性变形的门槛,在相同的冲击压力下,高温使得高熵合金内部的堆垛层错密度变大,产生更多的相变以及变形孪晶.在温度较高时,高熵合金更容易发生冲击诱导非晶化.

图13 给出不同变形机制的演化过程.图13(a)给出的位错运动是冲击压缩下高熵合金最重要的塑性变形机制.对于单元素单晶体,位错的均匀成核是冲击压缩下的基本变形机制,但对于高熵合金,由于多个元素原子尺寸差异导致的原始晶格畸变,冲击压缩下的位错成核不再均匀分布,而是更容易在原始晶格畸变较大的地方(例如Mn 元素周围)出现.同时在初始高温较高的情况下,位错也容易在局部能量较高的无序团簇处成核.如图13(a)中的9.1 ps,圆圈标识出了一个位错成核源,随后位错在〈111〉 平面上滑移扩展.当存在多个位错源时,多个位错会同时运动,在9.5 ps 时两个位错相遇,从而在高熵合金内部形成交叉网状的堆垛层错.图13(b)给出了冲击诱导下高熵合金发生相变的演化过程.由于较大的冲击压力作用,在冲击波前沿后面,BCC 结构可通过两个FCC 结构所形成的体心正方晶体(body-centered tetragonal,BCT)结构沿着[001]方向压缩,以及沿着[110]方向拉伸得到[25],在其他FCC 金属晶体的冲击压缩中也发现了类似的FCC 到BCC 的相变现象[46].图13(c)是变形孪晶的演化过程,在5 ps 时大量的FCC 结构转变成BCC 结构和HCP 结构,随后在9 ps 时出现多个包含孪晶结构的晶粒,图中标识出了典型的孪晶界(twin Boundary).在演化过程中孪晶界方向发生偏转,在15 ps 时几乎和冲击方向[001]一致.同时不同方向的孪晶也相互作用,合并成为尺寸更大的方向相同的孪晶.而且相对于相变和位错扩展,变形孪晶需要更长的演化时间.图13(d)给出了冲击诱导非晶化的演化过程,在受到强冲击压缩时原子受到强烈挤压从而远离原始位置,使得原有的FCC 结构转变成无序结构.从RDF 可以看到,第二峰并未完全消失,和完全熔化时的RDF特征(图2(a))有着明显区别,所以这里沿用Jian等[22]的描述,采用非晶化来描述此时的结构特征.

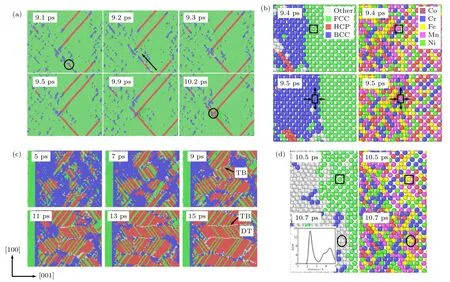
图13 不同变形机制的演化示意图 (a) 位错滑移;(b)相变;(c)变形孪晶;(d)非晶化Fig.13.Schematic diagram of different deformation mechanisms: (a) Dislocation slip;(b) phase transition;(c) deformation twinning;(d) amorphization.

4 结论

本文利用分子动力学方法,研究了温度对CoCr FeMnNi 高熵合金冲击响应和塑性变形机制的影响.分析了沿[001]冲击方向上,不同初始温度和冲击强度下的冲击压力、剪切应力、冲击速度和温度等的剖面图特征,通过冲击参量剖面图随时间的变化计算得到冲击HugoniotUp-Us曲线.以流动应力随冲击压力的变化特征和位错运动为判断依据,确定了CoCrFeMnNi 高熵合金的冲击HEL.利用PTM 方法,得到了不同初始温度和冲击强度下的缺陷结构.根据不同元素在不同结构中的占比、以及不同元素的原子体积,分析了在不同温度下各元素对冲击诱导塑性的贡献.具体结论如下:

1) 在相同的Up下,初始温度的上升使得冲击压力下降.例如当Up=1.5 km/s 时,1000 K 时的冲击压力相比于1 K 时下降了6.7%.同时冲击波在高熵合金内的传播速度(Us)下降,冲击诱导温升下降.

2) 在塑性阶段CoCrFeMnNi 高熵合金的冲击HugoniotUp-Us曲线可以通过公式Us=c0+sUp线性拟合.c0存在温度依赖性,随着温度的上升而下降.同时在HEL 处的冲击压力随着温度的升高近似线性下降.

3) 较高的初始温度使得CoCrFeMnNi 高熵合金内出现无序团簇,Mn 元素在无序团簇中的占比含量最大,约为25.4%.在冲击压缩过程中,冲击波前沿后面由FCC 结构转变成的BCC 结构和无序结构、以及高温下原始的无序团簇是位错成核的重要来源.区别于传统单晶冲击压缩下的位错均匀成核机制,由于高熵合金存在多个组成元素且各元素原子大小不同,位错的非均匀成核是其最基本的塑性变形机制.对于CoCrFeMnNi 高熵合金,Mn 元素原子体积相对较大、势能较高,所以Mn 元素较多的区域更容易成为位错成核源,这和Liu 等[25]的研究结论相一致.不同元素按对塑性变形的贡献从大到小排序依次为: Mn,Fe,Cr,Ni,Co.在温度较高时,Fe 元素对塑性变形的贡献和Mn 元素一样重要.

4) 随着冲击压力的增加,CoCrFeMnNi 高熵合金内部发生了复杂的塑性变形,主要的变形机制包括位错滑移、相变、变形孪晶和冲击诱导非晶化.在相同的初始Up下,初始温度的升高使得各变形机制更容易发生.在冲击压力相对较低时,位错滑移使得CoCrFeMnNi 高熵合金内部产生交叉网状的堆垛层错,堆垛层错的密度会随着初始温度的升高显著增加.随着冲击压力的上升,FCC 到BCC的相变发生在冲击波前沿后面,BCC 结构通过BCT结构沿着[001]方向压缩、以及沿着[110]方向拉伸得到.在冲击压力相对较高时变形孪晶是主要的变形机制,在CoCrFeMnNi 高熵合金内部出现沿[001]方向发展的孪晶界,相对于位错滑移和相变,变形孪晶需要更长的演化时间.在冲击压力和温度非常高时,出现了冲击诱导非晶化.