火星大气频散声速剖面建模方法及其对声传播路径的影响*

孙冠文 崔寒茵 李超 林伟军

1) (中国科学院声学研究所,声场声信息国家重点实验室,北京 100190)

2) (中国科学院大学,北京 100049)

火星声探测技术逐渐成为火星探测的一种重要手段.为了探测火星声源,需研究稀薄低温火星大气中的声速和声衰减、建立分层大气中的声传播模型.本文提出了一种结合Navier-Stokes (NS)声波方程和变组分混合气体的声速模型,考虑了火星极端稀薄大气中的声频散,将火星声速剖面模拟计算拓展到0—250 km 海拔范围,并讨论了NS 声速剖面的适用条件.本文实验验证了低压、低温环境中,在分子平动、旋转和振动弛豫作用下,三原子二氧化碳中存在明显声频散.随后分别基于频散NS 声速和无频散理想气体声速剖面,模拟了地面声源和高空声源产生的不同频率声波的传播路径.研究发现声频散显著影响了声传播路径,降低了声线首次折返高度、缩短了声线折回火星地表的距离、减小了第一声影区的范围等.而且频率越高、声源海拔高度越高,频散对声传播的影响越剧烈,NS 方程的连续性假设失效,更高频的声波需要基于Boltzmann 方程和分子模拟法建立声频散模型.

1 引言

火星是太阳系中与地球最类似的行星,具有很高的研究价值.声探测是探索和认知火星环境的一个重要新手段,被动声传感器可监测火星上可能存在的声音、并反演声源特性.2021 年NASA“毅力号”火星车携带了两套声学系统,分别记录了激光超声(>2 kHz)以及旋转叶片(84 Hz)的声信号,测量了火星声速,观察到高频声波比低频声波的声速高了约10 m/s,证明了火星稀薄大气中存在声频散现象[1].同年我国“祝融号”火星车成功登陆火星,携带的光纤声传感器也记录到了火星声信号[2].声波在火星稀薄、低温、时变、分层大气中会发生反射、折射、散射和吸收等物理过程,具有复杂的传播路径.为更好地分析火星车记录到的声信号,首先需要准确模拟声波在火星大气中的传播路径,进而反演声源类型、位置和强度,获取火星环境及气候参数等[3−6].模拟声传播路径的前提是获取准确的火星大气声速剖面[7].

火星上可能探测到高空声源的声信号,如火流星、放电、沙尘暴等[8].探测高空声源需要考虑火星高层大气的独特性质.火星极端稀薄、低温的大气与地球表面大气差异很大.火星表面大气压强为150—1350 Pa,约为地球表面气压的1%,随海拔升高,火星大气压强还会迅速降低,到250 km 海拔处仅为10–8Pa.火星表面大气气体成分以二氧化碳为主(95%二氧化碳、2.7%氮气、1.6%氩气和少量其他气体);气体成分随着海拔升高会发生显著变化,海拔150 km 以下主要成分是二氧化碳,150 km 以上主要成分变为氧原子.另外,火星温度在–130—25 ℃之间,比地球上的平均气温要低很多.声音的传播与温度、气压、大气组分、湿度和频率等因素密切相关,因而火星低温、稀薄、二氧化碳为主的大气中声传播的特性与地球上存在巨大差异,火星声速剖面建模的重点在于准确模拟极低气压、低温环境中变组分气体的声速.

极端低压气体中存在声频散现象(即声速随频率变化).一般来说,在标准大气压下单一气体中的声速与频率无关.但在火星极低气压环境中,分子平均碰撞频率较低,当声波频率与分子平均碰撞频率接近时,声速会随着两者比值(f/fc)的变化而变化,这就是稀薄气体中的声频散.

国内外逐步建立了不同的理论和数值模型来模拟不同稀薄程度气体中的声频散.通常使用Knudsen (Kn)数来描述气体稀薄程度,Kn数等于气体分子平均自由程与声波波长的比值[9].在Kn数较小(Kn<10)时,可基于Boltzmann 方程的数值解计算声频散.早在1896 年,Rayleigh[10]基于连续介质假设,利用Navier-Stokes 方程(Boltzmann 方程的一阶近似)首次讨论了黏性流体中的声频散.当气体比较稀薄(Kn>0.5)时,连续介质假设失效,可用Boltzmann 方程的高阶近似,例如Burnett 或Super Burnett 理论[11,12]来计算单原子气体的声频散.其中Sirovich 和Thurber[13]基于麦克斯韦分子假设、利用11 阶矩方法计算了多种单原子气体中的声频散,与实测数据符合较好.

以上方法适用于求解单原子气体中因平动弛豫引起的声频散,尚未考虑多原子分子中旋转和振动弛豫的影响.1946—1960 年Greenspan 扩展了经典理论,利用分子弛豫等效热容建立了考虑了双原子分子旋转弛豫的理论模型[14−17].

当气体特别稀薄(Kn>10)时,Boltzmann 方程不再适用,可以采用粒子方法来计算声速[18−20].2001 年,Hadjiconstantinou 和Garcia[21]用直接模拟蒙特卡罗(DSMC)法计算了极稀薄单原子分子中的声频散,比上述Boltzmann 数值解法更接近实验数据.2008 年Hanford[22]在DSMC 方法中引入了Borgnake-Larsen 模型来计算双原子旋转弛豫对氮气声频散的影响.后续DSMC 方法广泛地应用于稀薄气体中的声波计算,在2016 年和2019 年,Kalempa 等[23,24]将DSMC 方法用于混合稀薄气体中的声波计算.此外国内外开展了单原子、双原子和干燥空气中的声速测量[15,25−27],验证了稀薄气体的声频散现象.

因高层稀薄大气中存在明显的声频散,学者们逐步将声频散效应引入了大气声速剖面的计算.1984 年,Bass 首次提出了地球大气声速剖面以及衰减剖面的计算方法[28].2004 年,Sutherland 和Bass[29]应用此方法计算了地球大气0—160 km 海拔范围内的声速和声衰减剖面,指出当海拔高于80 km 时,声频散不能被忽视.2001 年,Bass 和Chambers[30]根据分子弛豫等效热容理论,计算得到了火星表面不同频率声波的声速和声衰减系数.2012 年,Petculescu 和Achi[31]利用同样的理论并基于Cassini-Huygens 测量的土卫六大气数据,模拟了土卫六声速和声衰减剖面.2016 年,Petculescu[32]根据半经验声频散公式计算了0—40 km 海拔范围内的火星大气声速剖面,但该模型中气体成分固定为95%的CO2以及5%的N2,适用的海拔范围较小,如果要拓展到高海拔火星大气,还需要研究变组分稀薄气体的声速计算方法.2020 年,Trahan和Petculescu[33]根据弛豫理论预测了金星50—60 km 海拔由于金星云造成的声衰减.

火星大气具有低温、稀薄、变气体组分的特点,本文提出了一种利用Navier-Stokes (NS)方程计算0—250 km 海拔范围内声速剖面的方法.针对火星极端低压,首先实验验证了低压二氧化碳中存在明显的声频散现象,然后利用NS 方程计算了稀薄大气的声频散,讨论了火星大气声速剖面计算中NS 方程的适用范围.针对火星变组分混合气体环境,采用等效气体参数对火星大气中的变组分混合气体建模,拓展声速剖面适用的海拔范围.随后基于不同频率(0.01,0.1,1 Hz)下的NS 声速剖面与理想气体剖面,通过射线追踪方法模拟了地面和高空声源的声传播路径,考察声频散对于地面和高空声源声传播路径的影响,解释声速建模中考虑频散的必要性.

2 火星声速剖面

2.1 火星大气的环境参数

火星的声速剖面与其大气的环境参数密切相关,如大气的温度、压力、风速、气体成分等都会影响火星大气的声速.获取火星的大气环境参数剖面一方面可以分析火星大气的环境特征,根据环境的特点选取合适的声速计算模型;另一方面声速模型的计算中也需要代入这些大气环境参数.

在本文中火星的环境参数采用了MCD (the Mars Climate Database)[34,35]提供的火星大气数据.图1 给出的分别为“祝融号”火星车着陆位置(北纬25.1°,东经109.9°)与时刻(2021 年5 月15 日8 时20 分)的大气环境参数,包括气体成分(a)、温度(b)、气压(c)和水平风速(d)随海拔变化的曲线图.据图1 所示,火星乌托邦平原的大气具备多组分、低温、稀薄、时变的特征:

1)火星大气是一个混合气体环境,地面附近以二氧化碳为主,而到了海拔150 km 以上变为以氧原子为主,气体成分随海拔变化大;

2)火星大气处于极端低温环境中,气温在120—211 K 之间随海拔复杂变化,在50 和120 km 海拔高度附近存在两个温度极小值,这将有利形成类似于地球平流层和热层的高层大气声通道,声波可在声通道中长距离传播;

3)火星表面气压在900 Pa 以下,并且随着海拔升高、气压会迅速降低,到250 km 海拔气压仅为10–8Pa,所以在火星高层稀薄大气中会出现严重的声频散现象,在计算声速剖面时必须考虑声频散的影响;

4)火星表面平均风速为10 m/s,当发生尘暴时风速可达到150 m/s,对于声传播路径有巨大的影响.

2.2 理想气体声速

在不考虑气体黏性的均匀理想气体中,声波不存在频散现象,理想气体状态下的声速计算公式为

其中c0为理想气体声速,γ为气体的比热比,R=8.314 J/(mol·K)为普适气体常数,T为气体的绝对温度,M为气体的分子摩尔质量.

根据(1)式可以计算得到火星大气的理想气体声速剖面.(1)式中气体的比热比γ、温度T和分子摩尔质量M在火星大气中都随海拔的变化而变化,其中温度T随海拔的变化已经在图1(b)中给出.

分子摩尔质量随海拔的变化与气体成分的变化相关.(2)式为混合气体分子摩尔质量的计算公式:

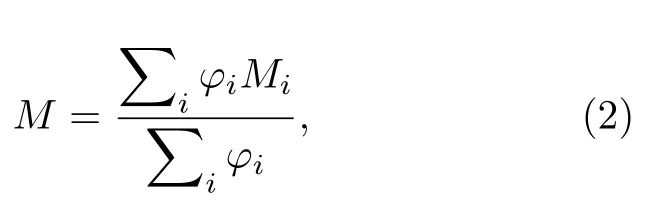
其中φi是每种气体的体积百分比,Mi是每种纯气体的分子摩尔质量.根据图1(a)中的气体成分随高度的变化以及表1 所列的火星每种气体成分的分子摩尔质量,可以计算火星大气混合气体的等效分子摩尔质量.计算结果如图2(a)所示,可以发现火星地表附近的分子摩尔质量约为44 g/mol,与CO2的分子摩尔质量接近,随海拔高度升高,分子摩尔质量逐渐降低,250 km 高空则约为16 g/mol,与氧原子的分子摩尔质量接近.

图2 火星大气(a)分子摩尔质量、(b)比热比和(c)理想气体声速的垂直剖面图Fig.2.Vertical profiles of (a) the molecular molar mass,(b) specific heat ratio,and (c) ideal gas sound speed of the Martian atmosphere.

表1 不同气体的分子摩尔质量Table 1.Molar masses of molecules of different gases.

而气体比热比γ随海拔的变化除了与气体的种类相关外,还是气体温度的函数.混合气体的比热比为

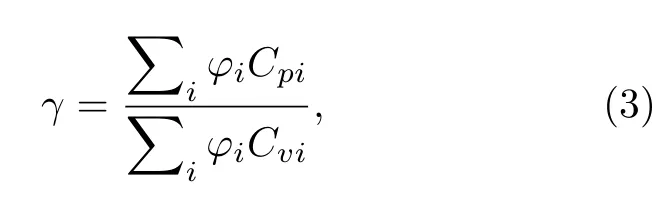
其中φi是每种气体的体积百分比,Cpi是每种纯气体的定压热容,Cvi是每种纯气体的定容热容.其中,每一种纯气体的热容是温度的函数,通常气体热容随温度的变化关系可用Shomate 公式((4)式和(5)式)来拟合实验数据得到:

本文的定压热容采用NIST Chemistry Web-Book 中由实验数据拟合得到的Shomate 公式[36]进行计算,其适用温度为150—6000 K,火星大气(120—210 K)基本满足其适用条件.6 种气体的公式系数在表2 中列出.计算得到的定压热容随温度的变化曲线如图3 所示.其中需要说明,由于单原子氧的热容的实验数据较少,无法进行Shomate公式的拟合,所以氧原子的热容使用理想气体热容公式计算,对于单原子气体,其分子有3 个自由度,根据能量均分定理,单原子氧的等容热容为3R/2,等压热容为5R/2.在低压下对于单原子分子气体,使用理想气体公式误差较小[37],如图3 所示,单原子氧和单原子氩气的低压定压热容基本一致.

图3 火星大气中6 种主要气体成分的定压热容随温度的变化Fig.3.Variation of the constant pressure heat capacity of the six main gas components of the Martian atmosphere with temperature.

表2 火星主要气体成分Shomate 公式系数Table 2.Shomate formula coefficients for the major gas constituents of Mars.

此外,由于气体的定压热容实验测量精度比定容热容更高,在低压条件下使用(6)式计算定容热容[37]:

随后,将每种纯气体定压热容代入(3)式计算得到火星气体比热比γ随海拔的变化,如图2(b)所示.在确定了火星大气的这3 项参数随海拔的变化关系后,可以根据(1)式计算得到火星分层大气中的理想气体声速剖面,如图2(c)所示.理想气体声速剖面未计及声频散现象,如在高层大气或者声波的频率较高,需要对其进行修正.

2.3 实验测量的低压二氧化碳气体中的声频散

为了验证稀薄气体中的声频散现象,进行了低温低压二氧化碳的声速测量实验.利用环境模拟器模拟低压低温的二氧化碳环境,气压控制范围为300—104Pa,控制精度为±10 Pa;温度控制范围为–80—20 ℃,温度均匀度为5 ℃.使用时差法测量声速,如图4 所示,3 对不同频率(21,34,40 kHz)的超声换能器相距为d正对固定,通过信号处理方法提取发射与接收信号的时差t0,利用(7)式计算得到不同条件下的二氧化碳声速:

图4 时差法测量声速实验装置图 (a)示意图;(b)实物图Fig.4.Diagram of the experimental setup for measuring sound speed by the time difference method: (a) Schematic diagram;(b) physical diagram.

实验测量得到的声速如图5 所示.由于稀薄气体中热交换较慢,在不同气压下控制环境模拟器中的温度恒定需要较长时间,所以实验中并未控制每一个气压下的温度,而是记录了每个实验工况下的温度.图5 中蓝色点线展示了实验中不同气压下的温度.如(1)式所示,理想气体声速与温度的开方成正比,而不随气压变化,在实验温度条件下的理想气体声速如图5 中黑色点线所示.实验测量的二氧化碳中声速(红色点线)在气压为104Pa 条件下与理想气体声速基本一致,0 ℃条件下实验测量声速与理想气体公式计算声速的差距为0.03%,–20 ℃条件下差距为0.14%.然而随气压的降低,实验测量声速与理想气体声速的差距呈现增大的趋势.当气压降低到500 Pa,0 ℃和–0 ℃温度下的实验测量声速与理想气体声速差别分别增加为1.30%和1.87%.

图5 二氧化碳中21 kHz 声波速度随气压的变化 (a) 0 ℃左右;(b)–20 ℃左右Fig.5.Variation of sound speed of 21 kHz sound wave with pressure in carbon dioxide: (a) Around 0 ℃;(b) around–20 ℃.

在低压情况下二氧化碳气体中出现了声波相速度随着压力的降低而变化.这是稀薄气体中的一种声频散现象,此外,声速还随频率而变化.前人将声速随频率气压比(f/p)变化的现象叫做稀薄气体中的声频散现象[38].从本质上讲,是由于声波频率f和分子平均碰撞频率fc逐渐接近,声弛豫现象变得更加显著.通常在一个大气压下,分子平均碰撞频率在1010Hz 左右,所以需要极高频(GHz)的声波才需要考虑声频散,但是由于火星高层大气中的气压极低,产生频散的频率也就随之降低,实验证明计算火星大气声速时必须考虑声频散的影响.但由于现有实验条件无法测量到极端低压CO2中的声速,因此本文用NS 方程计算稀薄气体中的声速.

2.4 Navier-Stokes 声速

在低压环境中,声波的相速度会由于黏滞效应而随频率与气压的比值(f/p)发生变化.在火星极端低压(10–8—103Pa)大气中,使用理想气体声速模型会产生较大误差,必须要考虑黏滞和热流的影响.可根据流体动力学中的Navier-Stokes (NS)方程来计算声速,首先定义声波传播时的复波数K:

式中,β=ω/c为实波数,其中ω是角频率,c是相速度;α为衰减系数.设平面波方程的形式为p′=其中p′为声压,为声压幅值,r为空间坐标.可通过气体状态方程、质量守恒方程、动量守恒方程以及能量守恒方程推导出关于复波数K的频散方程[22]:

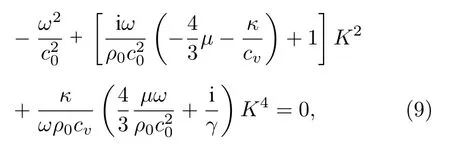
其中c0为利用(1)式计算的理想气体声速,ρ0为大气密度,µ为大气黏度,κ为热传导率,cv为等容比热,γ为比热比.

声波的相速度c1可以由(10)式解出:

其中定义了两个无量纲量,分别是R′=γp/(ωµ)=/(ωµ),P=κ/(µcv),根据(10)式,声波的相速度是无量纲量R′和P的函数,其中P仅与气体的性质相关,而雷诺数R′则与声波的频率相关.当雷诺数较小时,即气压和频率的比值较小时,火星大气中声速的相速度与频率相关.可以看出,Navier-Stokes 声速在理想气体声速的基础上进行了与频率相关的修正.

为准确求解NS 方程,需要首先计算火星多组分混合气体中的黏度和热导率随海拔高度的变化关系.采用低压下混合气体半经验公式(11)式和(12)式计算黏度[39],

其中

式中φi是每种气体的体积百分比,Mi是每种纯气体的摩尔质量,µi是每种纯气体的黏度.每一种纯气体的黏度都是气压和温度的函数.由于火星气压极低,气压对黏度的影响可以忽略[39],而温度对于纯气体黏度的影响可以用Sutherland 公式(13)拟合实验数据得到:

式中,T0和S为拟合参数.

根据Hirschfelder 等[40]的黏度测量实验数据(实验数据的温度范围为100—800 K,包含了火星大气的温度范围120—211 K),拟合得到的火星大气6 种主要气体成分的黏度随温度的变化曲线如图6 所示.随后结合温度剖面和气体成分剖面,可以计算得到火星多组分大气的黏度剖面,如图7(a)所示.

图6 火星大气6 种主要气体成分在100—300 K 温度范围内的黏温曲线Fig.6.Viscosity-temperature curves of the six main gas components of the Martian atmosphere in the temperature range of 100–300 K.

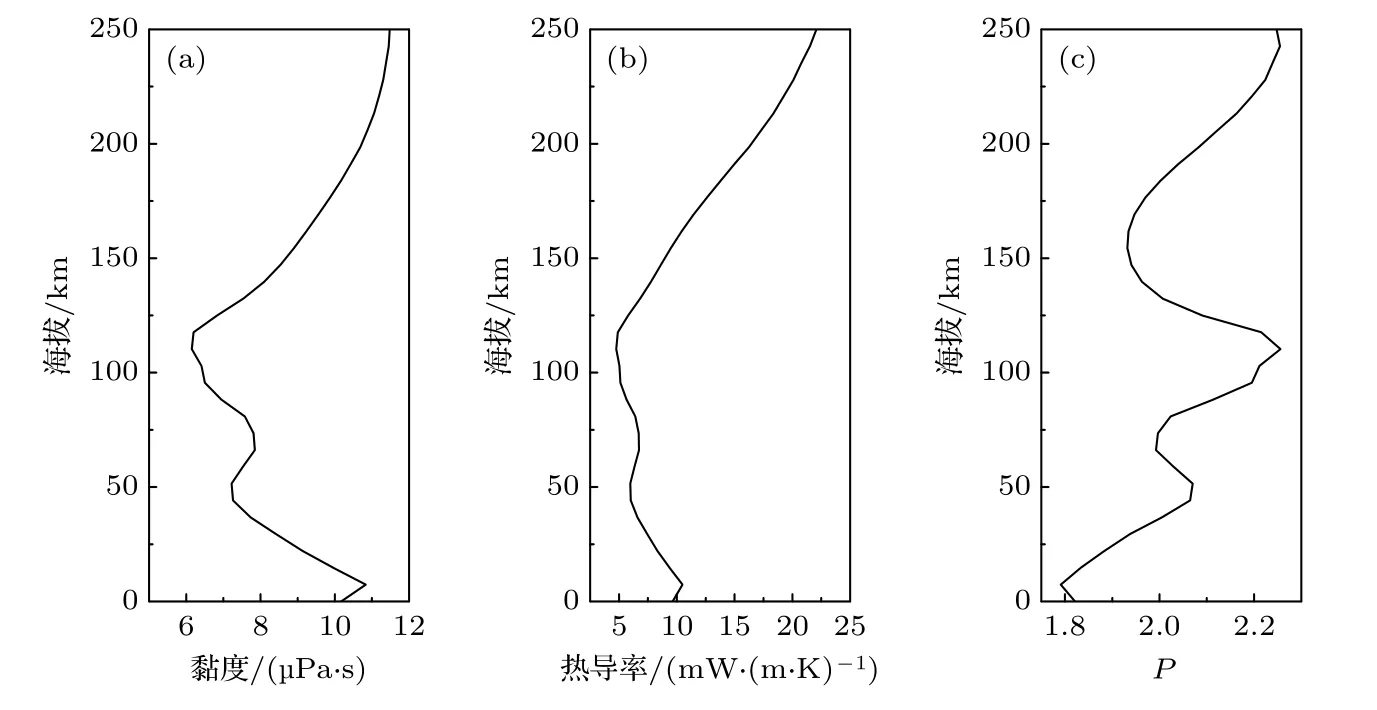
图7 不同海拔下火星多组分混合大气中的(a)黏度、(b)热导率和(c)无量纲数P 的垂直剖面图Fig.7.Vertical profiles of (a) viscosity,(b) thermal conductivity,and (c) dimensionless number P in the multi-component mixed atmosphere of Mars at different altitudes.

模拟低压混合气体中热导率的半经验公式为[39]

其中

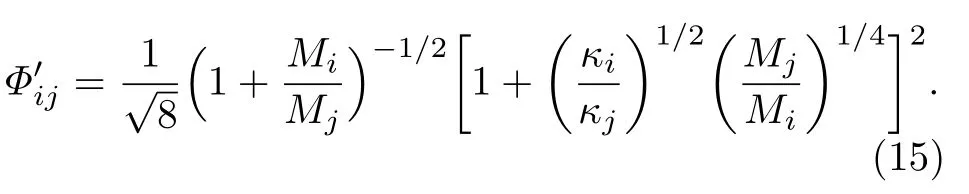
而对于每一种纯气体,由于气体热导率的实验测量难度很大、测量数据的准确度较低,通常都采用气体热导率和黏度之间的关系来推算热导率[27].本文采取Eucken 关系式(16)来计算每种纯气体的热导率:

(10)式中定义的无量纲数Pi满足(16)式.这里,φi是每种气体的体积百分比,Mi是每种纯气体的摩尔质量,κi是每种纯气体的热导率,γi是每种纯气体的比热比.

计算得到的火星大气热导率剖面以及无量纲数P剖面分别如图7(b)和图7(c)所示.

基于NS 方程模拟出的火星大气中不同频率声波的声速剖面如图8 所示.声波的相速度随着频率升高而逐渐变大,在高海拔区域尤其明显,这是由于海拔越高、气压越低,稀薄气体的声频散现象越显著.

气体的稀薄程度通常用Kn数表征,它等于分子平均自由程L与流场特征长度(声波波长λ)的比值,也就是声波频率f与气体碰撞频率fc之比.需要注意的是,当声波频率较高、接近于分子间碰撞频率,或气压极低、波长与分子平均自由程相当时,Kn数不是很小,气体分子的离散结构会显现出来,则破坏了连续介质力学适用条件,NS 方程不再适用.需要采用分子动理论进行分析.例如图8 中,利用(10)式计算出的1 Hz 声波的相速度在250 km海拔高度处达到了30 km/s,此时f/p ≈108Hz/Pa,分子间断效应很明显,NS 声速是不适用的,需采用非连续介质中的Boltzmann 方程或分子模拟方法来求解声速.

图8 不同海拔下、不同频率的声波在火星大气中的NS方程声速剖面,其中虚线代表NS 声速不适用的海拔范围Fig.8.NS equation sound speed profiles in the Martian atmosphere for sound waves at different altitudes and frequencies,where the dashed line represents the altitude range where the NS sound velocity does not apply.

NS 方程不适用的条件如(17)式所示[18]:

由于(17)式所示的失效条件与声波波长有关,因此不同频率的声波,其失效的海拔高度有所不同,NS 方程失效的区域在图8 中用虚线标出,不同频率下具体失效的海拔数值如表3 所列.

表3 火星大气中不同频率声波NS 声速适用失效海拔范围Table 3.Applicable failure altitude range of the NS sound speed for different frequencies of acoustic waves in the Martian atmosphere.

2.5 火星大气的声吸收

在考虑声线传播路径的同时,不能忽略声波幅度的变化.火星大气的环境是一个以稀薄的二氧化碳为主的环境,除了较低的气压带来更强的声吸收,二氧化碳为主的环境也使得火星大气中的声吸收远大于地球大气.根据Bass 和Chambers[30]提出的火星大气声吸收模型,二氧化碳作为三原子分子,其中的振动弛豫声吸收占据主导地位,尤其是在低频的情况下.这是火星大气与地球上以双原子分子为主的环境所不同的.根据Bass 和Chambers[30]的火星大气声吸收模型以及火星大气环境参数,可以计算得到火星的声吸收系数随海拔的变化曲线,如图9 所示.对比火星大气对于高频声波的高吸收系数,对于低频声波,火星大气的吸收与地球的相接近.即使在150 km 海拔的高空,每百千米的传播衰减为10 dB 左右,所以,在远距离可以接收到大幅度脉冲声源的低频成分.因此研究火星大气中低频声波的远距离传播模型具有实际应用价值.

图9 火星大气中0.01 Hz 声波的声吸收系数随海拔的变化Fig.9.Variation of the acoustic absorption coefficient with altitude for 0.01 Hz sound waves in the Martian atmosphere.

3 火星大气声传播路径模拟与分析

计算火星大气声速剖面的目的是计算声传播路径,最终通过接收信号反演声源的位置和特征.由于空间尺度较大,射线跟踪方法是大气中常用的计算声传播路径的手段.本文基于理想气体声速剖面和不同频率下的Navier-Stokes 声速剖面,计算火星大气中的声传播路径,分析声频散对于火星声线传播的影响.此外,针对地面和高空声源,分析了频散对于不同海拔高度声源声传播路径的影响.

3.1 频散对声线传播路径的影响

根据第2 节中计算的理想气体声速,以及0.01,0.1,1 Hz 声波的NS 方程声速这4 种声速剖面,通过求解声波的程函方程分别计算出4 种声速模型下的声传播路径[41],如图10 所示.

对于理想气体声速剖面来说,由于温度随海拔的变化梯度较小,部分大角度发射的声线只会发生方向的改变,不会折回地面;当发射角小于50°时,声线会由于高海拔下的高声速区域向下弯折、返回地面,返回高度在240 km 左右.并且与地球类似,火星声传播也存在声影区,影区宽度在550 km 左右.

然而如图10(b)—(d)所示,随着频率的升高,声线首次折回的海拔高度逐渐降低,地面的影区范围也逐渐减小: 不同频率下具体的声线首次折回高度以及地面影区范围的数据如表4 所列.对于1 Hz的声波,考虑频散后声线折回高度降低40.4%、影区范围缩小69.8%,且频率越高,折回高度和影区变化越剧烈.这是由于考虑了声频散的NS 声速模型与气压相关,在火星高海拔的低气压环境下,NS 声速在高海拔区域的声速比理想声速模型更快,随着海拔的升高(气压的降低),声速也逐渐升高,声线会向着声速小的方向弯折、再返回低海拔区域.随着频率增大,声频散现象更加严重,声线折回的海拔高度随之降低.

图10 火星不同声速剖面模型下声传播路径预测 (a)理想气体声速;(b) 0.01 Hz,(c) 0.1 Hz 和(d) 1 Hz 的声波NS 声速,其中不同曲线表示声线向不同角度发射,射线发射角度范围15°—60°,角度间隔3°,水平范围0—700 kmFig.10.Predicted sound propagation paths for different sound speed profile models of Mars: (a) Ideal gas sound speed;(b) 0.01 Hz,(c) 0.1 Hz and (d) 1 Hz NS sound speed,where different curves indicate sound lines emitted at different angles,with ray emission angles range from 15° to 60°,angular interval 3°,horizontal range 0–700 km.

同时,基于NS 声速的声传播路径计算必须结合NS 的适用范围.根据表3 不同频率下NS 声速在火星大气中的适用海拔,结合表4 中声线折回高度,可以发现声线折回高度均满足NS 声速的适用范围,因此可以使用NS 声速计算0.01—1 Hz 低频声波的声传播路径.

表4 不同声速剖面下的声线对比Table 4.Comparison of sound lines at different sound velocity profiles.

3.2 声源高度对声传播路径的影响

计算得到的不同海拔(50,110,150 km)下的高空声源在理想型气体剖面条件下的声线路径如图11(a)、图11(c)和图11(e)所示,50 和110 km高度的声源发出的大角度声线和地面声源一样会因为高空的声速增大而返回地面,而小角度发射的声线由于50 km 和110 km 附近的声速极小值会形成高空声通道(波导层),并在此通道内传播很远的距离.

图11 声源高度对声传播路径的影响.基于理想气体声速剖面的 (a) 50 km,(c) 110 km,(e) 150 km 高度声源的传播路径;基于0.01 Hz 声波的NS 声速剖面模拟的(b) 50 km,(d) 110 km,(f) 150 km 高度声源的传播路径;其中不同曲线表示声线向不同角度发射,射线的发射角度–45°—45°,角度间隔3°,水平范围0—700 kmFig.11.Effect of sound source height on sound propagation paths.Propagation paths of sources at (a) 50 km,(c) 110 km,and(e) 150 km based on ideal gas sound speed profiles;propagation paths of sources at (b) 50 km,(d) 110 km,and (f) 150 km based on simulated NS sound speed profiles of 0.01 Hz sound waves;where different curves indicate sound lines emitted at different angles,with ray emission angles range from–45° to 45°,angular interval 3°,horizontal range 0–700 km.

利用相同的声线计算方法计算得到了火星大气0.01 Hz 声波的NS 声速剖面下的声传播路径,如图11(b)、图11(d)和图11(f)所示.对比两种声速剖面计算的高空声源传播路径,可以发现对于0.01 Hz 这样的低频声波来讲,低海拔声源的声传播路径差异较小,无论是声线首次折回高度或是首次返回地面距离,都基本一致.但对于150 km海拔的高空声源,声线路径存在明显的差异.其声线折回高度有着明显的降低,且由于向上发射的声线折回更快,在地面距离声源200—400 km 范围内声线呈现明显的汇聚.出现这种现象是由于在考虑了声频散后,对于低海拔处(相对高气压)频散对于声速的影响较小,而对于高海拔处(相对低气压)频散对声速的影响更大,这使得在高海拔区域形成了更大的声速变化梯度.声线的折射与声速变化梯度密切相关,这就导致了在考虑频散后,高海拔(150 km)声源声线折回高度明显降低.

上述结果表明,对于更高海拔的声源,声频散具有更明显的影响,因此在计算火星高空声源的声传播路径时,即使对于低频声源,也不能忽略频散的影响.

4 总结与讨论

本文提出了一种火星极端稀薄、低温、变气体组分、分层大气中的声速剖面计算方法,利用混合气体模型和考虑气体黏度的NS 方程,模拟了气压、气温、气体成分和组分、以及声波频率与声速和声衰减系数的关系,重点讨论了稀薄气体的声频散现象对火星声速剖面的影响.随后根据理想气体声速和不同频率下的NS 声速剖面计算了火星大气中的声传播路径,分析了频散对于声传播路径的影响,得到了以下主要结论:

1) 由于火星大气极其稀薄、气压极低,计及频散后的NS 声速剖面与理想气体声速剖面存在着明显的差异,尤其是高海拔区域的偏差巨大,因而计算火星大气声速剖面时必须要考虑声频散的影响.

2) 声频散会改变火星大气中的声传播路径.基于声频散的NS 声速模型模拟出的声线在逆温层的返回高度比理想声速的更低;并且频率越高,声频散越显著,声线的返回高度会进一步降低.

3) 基于频散与非频散声速剖面模拟的声影区(即声线首次折返到地面的距离)也存在显著差异,基于理想气体声速计算的第一声影区约554.3 km,随着频率增大,NS 声速计算的声影区范围逐渐缩小.因此,利用理想气体声速剖面预测的声影区面积偏大,不利于火星声探测的开展.

4) 对于火星可能存在的极光(放电)、陨石爆炸或坠落、旋风沙柱和沙尘暴等高层声源,声源的海拔位置越高,声频散对于声传播路径的影响也越显著.

5) 由于火星分层大气有逆温层,火星上也存在与地球类似的高海拔声波导(声信道),高空声源产生的信号会“陷入”波导层,使得信号很难在火星表面接收到,但在波导层中衰减较小、可沿着信道传播较远距离,未来可以用高空悬浮器(气球或气艇)开展火星高空声源的探测.

火星大气中的声波特性仍存在很多未知亟待解决.

首先,本文声速剖面的计算依赖于MCD (the Mars Climate Database)数据库提供的温度、气压、气体成分等火星大气参数,此数据库提供的数据基于火星大气循环的数值模型,而非实测数据,与实际的火星环境参数存在一定偏差.本文提供了一种声速的建模方法,可以根据火星大气的环境参数进行建模计算声速剖面.研究团队已经提交了“天问一号”火星气象测量仪数据的申请,批准后可用我国记录的数据进行分析模拟.

其次,本文提出的火星声速剖面计算方法是基于NS 方程,对于高层大气中的高频声波的声速计算适用性较差,因为当声波频率和气压的比值高于临界值时,气体的连续性假设失效,不能再用NS 方程计算声速.虽然高频声波在大气中的衰减较强,很难远距离传播,但可用高频超声做近距离的主动声探测,例如火星风速超声测量仪[42]可实时测量三维风场、火星车超声避障仪可以在沙尘暴时替代光学导航系统.未来可以使用Boltzmann方程的更高阶近似方程(如Burnett 方程等),或者直接使用粒子模拟方法(如直接蒙特卡罗分子模拟法等)计算高频声波在高层大气中的声速剖面.

并且,基于NS 方程无法考虑多原子分子的转动和振动弛豫对声频散的影响.而对于二氧化碳,振动弛豫对其声频散存在重要的影响.Greenspan[14−17,37,38]提出了对于多原子分子频散计算的修正方法,但其计算过程需要测量气体的弛豫碰撞数,对于火星大气这种混合气体环境,其弛豫碰撞数的计算仍需要探索.

最后,对甚低频声波传播路径的计算中尚未考虑重力的影响,当波长特别大时,重力会影响对于0.01 Hz 这种低频声波的传播路径,现有的声线模拟不够精确,只能作为定性的分析.此外,在火星大气极端低温、极低气压的环境中,声信号的发射和接收也十分困难,一是由于火星大气声衰减较大,接收信号信噪比较低,二是由于稀薄气体与换能器阻抗差距较大,声能量较多的反射.声传播路径预测仅是火星探测最基础性工作,未来需要研制适应火星环境的声传感器、发展适合火星声环境的信号处理算法来探索这个未知的星球.