基于集成光芯片的量子模拟研究进展*

陈阳 张天炀 郭光灿 任希锋

(中国科学技术大学,中国科学院量子信息重点实验室,合肥 230026)

量子模拟是利用可控的量子系统来模拟其他未知或难以控制的量子体系,通过这种方法来处理一些在经典计算机上无法进行仿真的复杂量子体系,用于如基础物理探索、分子动力学研究、药物研发等相关领域.集成光学系统是实现量子模拟的一个优秀的实验平台,能实现如无序系统、拓扑绝缘体、非线性和非厄米体系等凝聚态物理结构的模拟,或用于实现量子随机行走、玻色取样等以演示量子优越性.本文介绍多种量子模拟物理模型的理论基础,结合如硅、玻璃、铌酸锂等波导体系的优势,综述近年来利用集成光芯片实现量子模拟的研究进展,包括了在集成光芯片上基于模拟型和数字型这两类量子模拟实现凝聚态物理模型仿真、量子随机行走、玻色取样等,探讨集成光芯片上的不同的量子模拟技术的实用化前景和发展趋势.

1 引言

自1981 年费曼提出量子计算机的概念以来[1],虽然实现通用式量子计算机仍然是一个长期的目标,但实现一些复杂量子体系的量子模拟任务成为研究复杂物理问题如低温物理、多体物理的关键方法.在经典计算机上模拟量子体系时,由于描述量子态参数所需的存储空间随着系统尺寸指数增长,因此,利用可控的量子系统,例如超导系统、原子或离子体系、核以及电子自旋系统、光学体系等[2−5]实现量子模拟,可以有效解决在其他体系中难以模拟的任务.光学体系天然可以用于编码量子比特,具有较好的可操控性,如可以利用路径、偏振、轨道角动量等多种自由度来编码信息,且一般不需要低温环境.此外由于具有较好的消相干能力,光学系统是优异的承载量子信息的载体.在传统光通信技术中,光在自由空间传播过程中相位等信息容易受到外界环境干扰,集成光学系统可以利用光波导将光场束缚在微纳尺度,从而实现稳定的信息传输,因此在众多的光学体系中展现出独特的优势.近些年来,集成光学系统也因其小型化、稳定性高、规模可扩展等优势,在量子通信、量子计算等方向展现出实用化的应用前景[6−9].

得益于不同材料系统一些特有的优势,如相位可调节能力、三维加工能力、高非线性系数等,集成光学系统近十多年被广泛应用于实现如量子随机行走[10−14]、玻色取样[15−20]、拓扑绝缘体结构、非厄米以及非线性物理系统量子模拟[21−26].基于集成光学系统的量子模拟也被用于研究分子基态能量、分子动力学[27−29],可以潜在用于药物分子设计等关键技术.根据量子模拟设备不同的特性可以对其进行分类[2],如根据模拟设备实现量子系统细节的程度可区分为两类,一类是全局系统的量子模拟,用于研究如量子相变过程等;另一类通过对每一个量子比特的精确控制和测量来准确理解要模拟的量子体系的微观性质.另外,根据量子模拟设备实现量子操作的类型主要分为数字型(digital)和模拟型(analog)量子模拟.其中前者基于量子线路,一般包含了初态的制备、离散的量子逻辑门操作(可分解为单比特、两比特量子门)以及最终的态测量过程,如集成光学系统中的多端口干涉仪结构.后者由具有相似哈密顿量并且在一定程度上可控制的系统来实现量子模拟,如光波导阵列、光子晶体、耦合腔阵列等.

本文基于集成光学系统介绍其在量子模拟研究领域的进展以及发展前景: 从基本的物理模型出发,基于集成光学系统构建的晶格结构来介绍无序安德森局域化、拓扑绝缘体中的物理、非厄米以及非线性诱导的新物理现象;基于多端口干涉仪结构介绍量子随机行走、玻色取样、量子化学模拟等过程.通过对这些典型的、前沿的物理模型的梳理和介绍,并且讨论这些物理模型在集成光学系统上物理实现的实验进展,以期启发更多关于新奇物理模型的研究,助力于新物理现象未来的实际应用探索.

2 集成光学系统

构成集成光学系统的材料体系种类繁多,如硅基、铌酸锂、飞秒激光直写透明介质、III-V 组材料(InP 和GaAs)、稀土材料等实验平台[6,30−32].关于不同材料的优缺点和用途,读者可以查阅相应的文献,本文简要介绍目前几种应用于量子模拟的主流的集成光学材料体系: 1)硅基集成光芯片,如硅、掺杂二氧化硅、氮化硅波导等.一方面,通常所采用的互补金属氧化物半导体(CMOS)半导体加工技术经历了五十多年的发展,具有成熟的工艺;另一方面,由于该体系有较高的折射率对比度,因而具备较好的光场束缚能力,可以实现更加小型化、集成化的系统.基于硅的高三阶非线性系数,可以利用四波混频效应在硅基波导中产生量子光源[9,33−40],另外还可以集成超导纳米线实现光子探测.在量子模拟方面,基于热调相位的马赫-曾德尔干涉仪构建可重构的离散型量子网络可用于研究量子随机行走过程、量子化学模拟等,但存在相位调节的稳定性和调制速度慢的问题.2)铌酸锂基集成光芯片,在制备波导时通常采用质子交换或者钛扩散技术以实现芯层折射率的增大.该系统具有超低的损耗,较高的二阶非线性系数和电光系数,因此可以利用自发参量下转换过程制备量子光源[41−43].电调相位调制速度快的优势使其成为制备主动非线性器件(如光开关、频率转换器件)的优秀材料体系.此外,光子探测和电子学器件也可集成到这一系统中.目前该系统主要应用在实现量子通信功能,近来被用于研究非线性系统中的拓扑物理.作为一种新兴的可动态调控的材料,期望基于铌酸锂基的集成光芯片体系未来能够应用于实现更多物理模型量子模拟,并且结合量子光学发挥更多的实际用途.3)飞秒激光直写光芯片,通过物镜将短脉冲、高峰值功率的飞秒激光聚焦到透明材料(如玻璃、聚合物)中,触发非线性吸收过程从而改变聚焦位置处材料折射率.该系统利用高精度位移台控制样品的移动以决定波导走向,具备可三维加工、可快速制备的优势,因此利用飞秒激光直写技术制备的光波导阵列成为近些年实现一些难以控制的电子系统中的凝聚态物理模型量子模拟的优秀实验平台[31].该系统目前存在调制难度高,尺寸大的问题.

如图1 所示,在集成光学系统中,实现凝聚态物理模型量子模拟主要用到了光波导阵列、耦合环腔阵列、光子晶体等结构,这一类量子模拟可以归结为模拟型量子模拟;而基于级联的分束器或者马赫-曾德尔干涉仪的多端口干涉仪结构常被用于研究离散型量子随机行走、玻色取样、量子化学模拟等,属于离散型量子模拟.接下来介绍不同系统用于实现量子模拟的基本原理,将在第3 和第4 节中介绍这些结构在集成光量子模拟方面的研究进展.

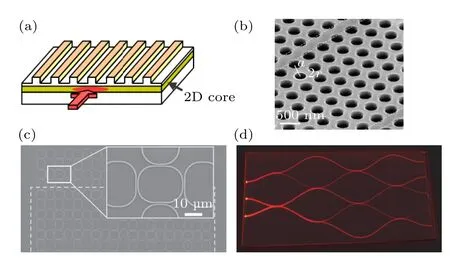
图1 几种常见的用于量子模拟的集成光学系统 (a) 耦合光波导阵列[44];(b) 光子晶体;(c) 耦合环腔阵列[45];(d) 多端口干涉仪[17]Fig.1.Several integrated optical platforms for quantum simulation: (a) Coupled optical waveguide array[44];(b) photonic crystal;(c) array of coupled ring resonators[45];(d) multiport interferometer[17].

2.1 光波导阵列

在傍轴近似条件下,任意T时刻在光波导阵列垂直于传播方向的横截面r⊥位置上的光场波函数Ψ(r⊥,T)(单波导有效折射率为neff,真空光波长为λ0)满足薛定谔形式的传播方程[25,46−48]:

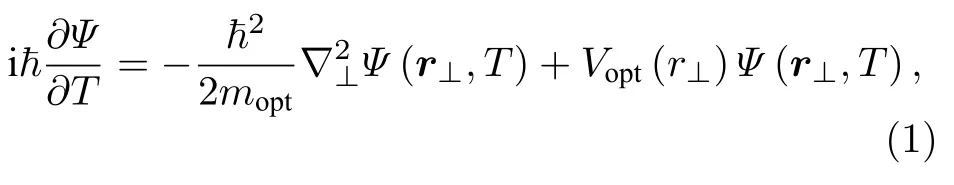
其中有效光学质量为mopt=ℏβ/v(光在波导中的群速度v=c/neff,传播常数β=neffk0,ℏ 为约化普朗克常数,波矢大小k0=2π/λ0),波导阵列r⊥处的折射率分布n(r⊥)等效为有效光学势场Vopt=(ℏk0c)×为了直观地与电子系统中的薛定谔方程对比,(1)式中光沿传播方向的演化转换成了光场随时间的演化关系.由于传播方程与量子力学中薛定谔方程的相似性,光在波导阵列中的传播类似于电子在固体系统(如周期晶格结构、无序系统、准晶结构)中的传播过程.光波导阵列系统中(通常考虑单模波导),每个波导位置处折射率分布对应于固体系统中的在位束缚势(on-site potential),每个波导的模式之间的重叠引起的光在波导之间的耦合对应着固体系统中电子隧穿(tunneling).通过控制波导阵列结构中折射率的空间分布,可以调制光在系统中的传播行为.1965 年,研究者基于耦合的光纤结构理论研究一维波导链中光的衍射行为[49],并随后于1972 年在等间距砷化镓波导阵列中实验观察到了光的弹道式扩散过程[50].目前描述耦合光波导阵列的能带分布以及光的传播普遍采用紧束缚近似模型处理,即从亥姆霍兹方程出发,把光在每个波导位置处的折射率分布作为零级近似,其他位置波导的折射率分布作为微扰项进行处理.紧束缚近似下,耦合光波导阵列的哈密顿量可以表示为[13]

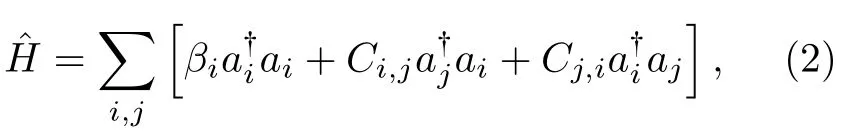
其中,βi是第i根波导的传播常数,Ci,j为光从第i根波导耦合到第j根波导的耦合系数,(ai) 为光在第i根波导的产生(湮灭)算符,满足玻色子对易关系.根据海森伯演化方程可以得到光在沿z轴传播的波导阵列中的传播方程:

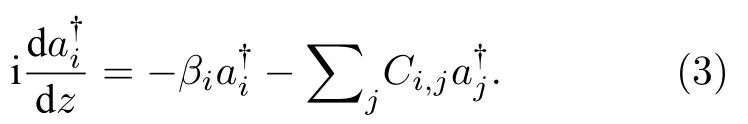
(2)式和(3)式是利用光波导阵列实现凝聚态物理模型量子模拟的基础,通过控制波导的折射率分布或者波导之间的间距,可以模拟周期系统连续型量子随机行走、无序系统安德森局域化等现象.

2.2 光子晶体

不同于光波导中光场通常束缚在高折射率介质中,基于光子晶体的波导其光场可以在低折射率介质中传播,并且可以在结构中实现剧烈角度的弯折.光子晶体是由高低折射率交替变化的介质材料组成的周期性介电结构,其周期长度与光波长的数量级相近.光子晶体具有类似于固体物理的晶格结构,按照周期排布方式可以分为一维、二维和三维光子晶体.光子晶体中光的传播依赖于周期结构中的布拉格反射过程,当入射光的波长接近光子晶体的晶格周期时,这种周期结构界面处的多重反射光会发生干涉从而形成光子能带.特别地,在折射率差较大的光子晶体结构中将出现光子带隙(对于具有特定偏振在一定频率范围内的特定方向入射的光全部反射).

如图1(b)所示,以二维光子晶体为例(电介质中的空气孔或者空气中的电介质),介质介电常数ε(r)在(x,y)平面内周期排布,其磁场满足布洛赫定理,因此可以表示为Hn,k(r)=eik·r·un,k(r),其中n,k分别是能带数和波矢,un,k(r) 和晶格具有相同的周期性.电介质中频率为ω的磁场满足如下传播方程[51]:

其中c表示真空光速,且有∇·H(r)=0,结合布洛赫定理求解本征值方程(4)可以得到周期性光子晶体结构中横电模(TE)和横磁模(TM)的能带结构.在光子晶体结构中通过引入线缺陷可以破坏晶格结构的对称性从而在缺陷位置形成缺陷态,通过设计晶格结构可以使缺陷态处在光子带隙中,这种方法被用于制备光子晶体波导[51−53].近些年来,研究者开始利用紧束缚近似模型求解光子能带[54−57],从而在光子晶体结构中实现拓扑绝缘体结构的模拟,进而实现在微纳结构中光的方向性操纵和鲁棒性传输.

2.3 光学腔阵列

耦合腔阵列是由多个通过倏逝场耦合的具有高品质因数(Q值)回音壁模式的光学微腔或者缺陷腔构成[58].考虑弱耦合的情况(耦合光学腔阵列中单个腔的模式可以用独立的腔模近似),类似于光波导阵列和光子晶体的处理方式,耦合光学腔阵列系统可以利用紧束缚近似模型来求解光子能带及本征电磁场分布.光学微腔可以支持多个简并的模式,如图2 所示的顺时针和逆时针光学模式(赝自旋),相邻两个环腔之间通过连接的波导实现光的耦合.基于图2(a)所示的结构,Hafezi 等[59]于2011 年提出可以实现量子自旋霍尔系统的模拟,基本原理是设计环腔和连接波导的长度保证光分别在两个结构中发生相长和相消干涉,从而将光束缚在环腔中.同时要求连接左右两个环腔的上下分支波导的长度不同,使得顺时针/逆时针光学模式从左边耦合到右边和与之相反方向上的耦合存在相位差异,并且与赝自旋有关.描述图2(a)所示的二维方格子耦合环腔阵列的哈密顿量为

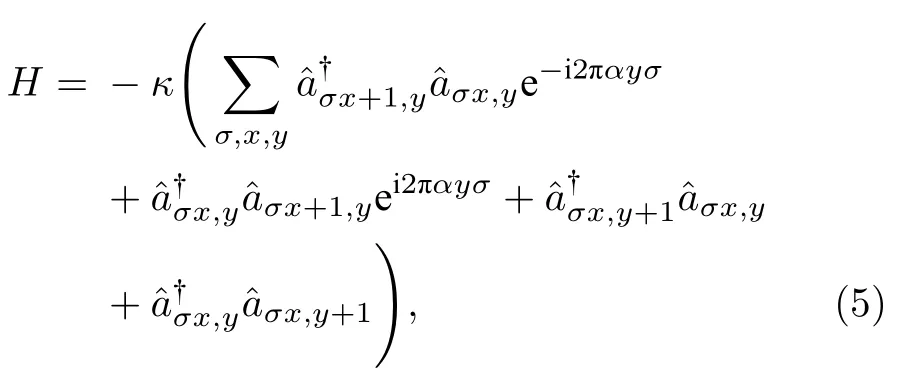
其中κ是相邻两个环腔之间的耦合系数,是光子在位置为(x,y)处的赝自旋σ=±1 (顺时针/逆时针光学模式)的产生(湮灭)算符.对于两个正交的赝自旋模式,光子沿着由相邻的4 个环腔构成的闭合路径运动时将获得一个与赝自旋有关的相位,这种行为类似于带电粒子在外加磁场下沿闭合路径运动积累的Aharonov-Bohm 相位.由这样的单元组成的周期耦合环腔阵列可以实现光子的有效磁场,进一步被用于模拟量子自旋霍尔效应,在每个赝自旋表象下对应着整数霍尔效应系统.Hafezi 研究组[45]的这一构想随后被他们于2013年在硅光子芯片上实现,他们通过输入波导耦合进频率与拓扑边界模式共振的激光,观察到了拓扑边界态的传播,随后他们又利用该系统研究了边界态的鲁棒性的传输和拓扑数的测量.2013 年,Chong研究组[60,61]在上述模型的基础上调制描述两个环腔之间耦合的散射矩阵(图2(b)),系统表现出了周期驱动(Floquet)拓扑绝缘体的能带结构,该模型不需要精细调节连接波导引起的相位;2020 年Afzal 等[62]首次在微纳光学系统(硅基八边形腔阵列系统)实现了这种反常Floquet 拓扑绝缘体[62].2018 年,Leykam 等[63]设计图2(c)所示结构[63],通过中心连接环波导实现格点环腔之间的近邻和次近邻耦合(类似于Haldane 模型[64]),随后他们利用硅环腔结构实现了这种反常量子霍尔系统模拟(零磁通量),并观察到了鲁棒性的拓扑边界态的传输[65].

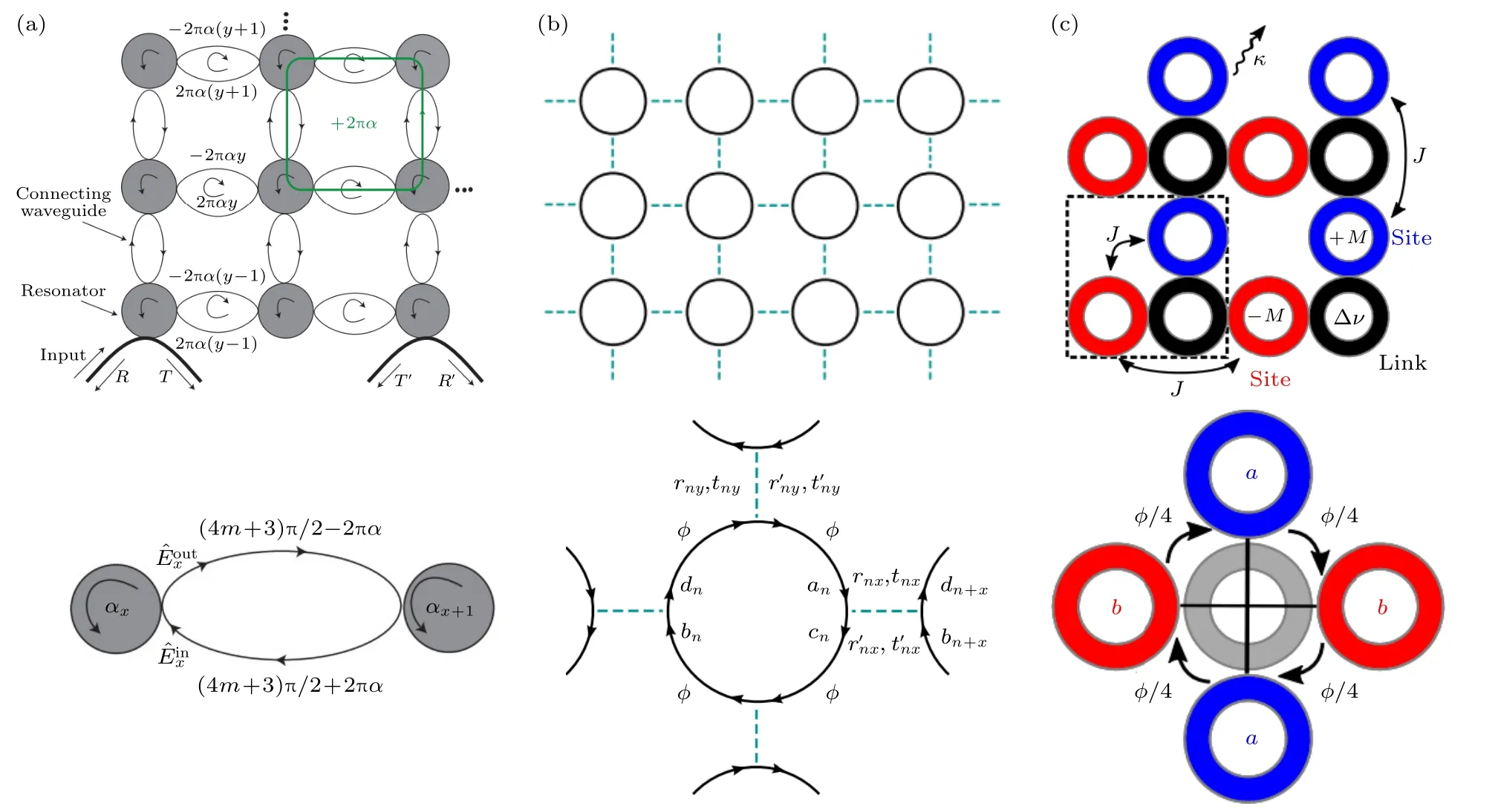
图2 用于模拟拓扑绝缘体结构的耦合环腔阵列 (a) 量子自旋霍尔效应系统[59];(b) 周期驱动Floquet 拓扑绝缘体结构[60];(c) 反常量子霍尔效应系统[63].(a)—(c)上列为周期阵列结构,下列为周期结构中基本单元的物理图像Fig.2.Arrays of coupled ring resonators for simulations of topological insulators: (a) Quantum spin Hall effect[59];(b) Floquet topological insulators[60];(c) anomalous quantum Hall effect[63].The upper panel in (a)–(c): periodic coupled resonator arrays;lower panel: basic units in the periodic structures.

2.4 多端口干涉仪

多端口干涉仪主要由分束器和相移器组成,可以实现多端口的任意幺正变换.1994 年,Reck 等[66]最早提出图3(a)所示的三角形结构,随后2016 年Clements 等[67]提出矩形结构的多端口干涉仪结构,使得原先实现N端口任意幺正变换的结构深度缩短到N步.这两种结构能够实现N端口任意幺正变换的原理都是基于对幺正矩阵的分解,通过将某一特定幺正矩阵多次分解得到对角矩阵,分解过程可以拆分成多个变换矩阵Tp,q相乘(变换矩阵仅作用在p,q两个端口).对角矩阵实验上通过处在特定端口的相移器实现,变换矩阵Tp,q由可调分束比的分束器和相移器实现.这两种构型的多端口干涉仪可用于实现离散型量子随机行走、玻色取样以及量子化学模拟等研究.

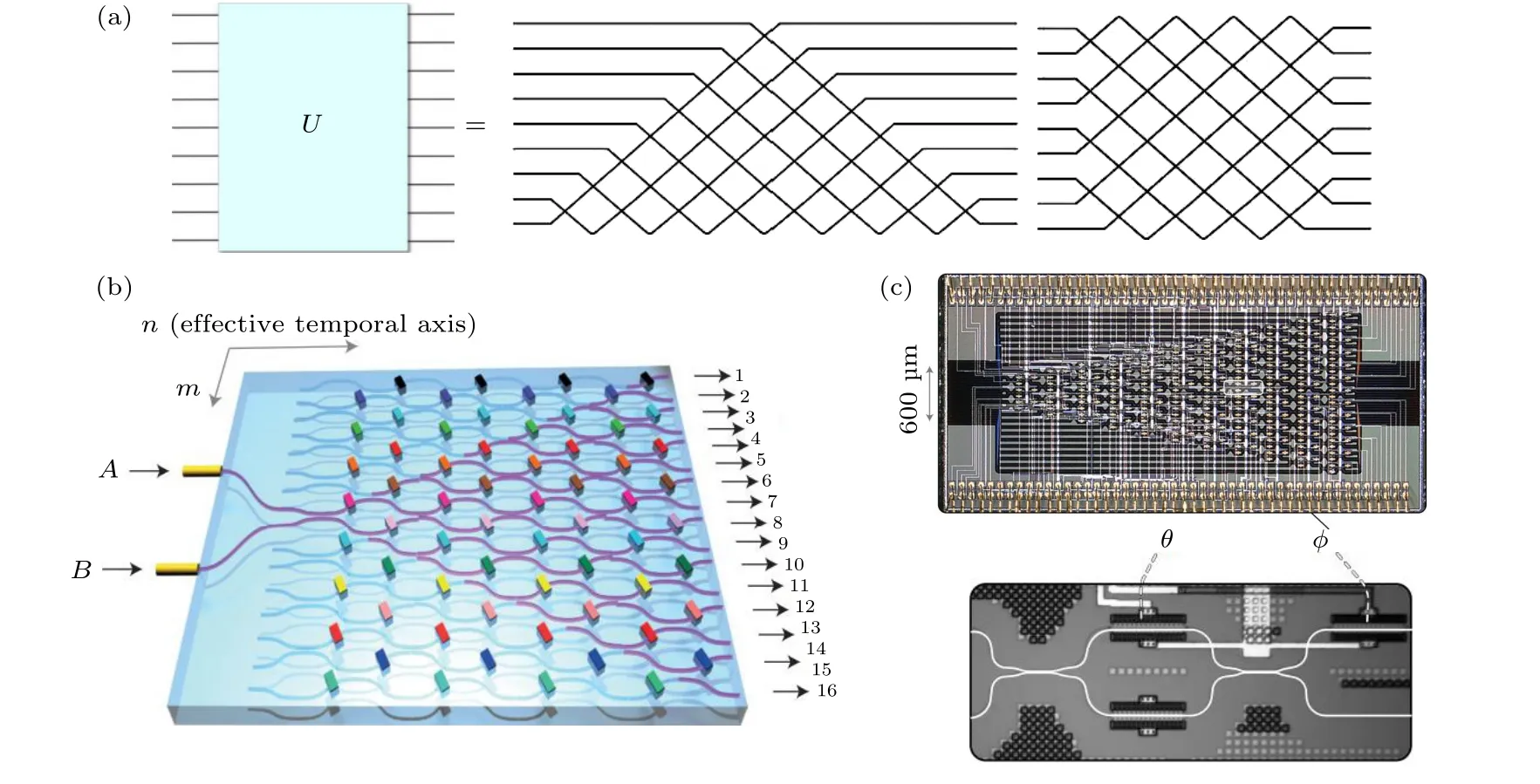
图3 多端口干涉仪用于量子模拟 (a) 三角形结构(左)[66]和矩形结构(右)[67]的多端口干涉仪用于实现任意的幺正变换;(b)双光子在离散型量子随机行走芯片中的安德森局域化现象[14];(c) 硅基多端口干涉仪[68],由可调马赫-曾德尔干涉仪组成Fig.3.Multiport interferometer for quantum simulation: (a) Realizing arbitrary unitary operator using triangular (left)[66] and rectangular (right)[67] mesh of beam splitters;(b) two-photon Anderson localization in discrete-time quantum random walk circuits[14];(c) multiport interferometer in a silicon-on-insulator platform[68],which is consist of tunable Mach-Zehnder interferometers.

3 模拟型量子模拟

3.1 无序系统

无序系统普遍出现在固体物理体系中关于输运过程、电导等的研究[69−72],1958 年,Phillip Anderson[73]提出晶格结构中的无序导致电子局域化(安德森局域化),随后Mott[74]提出迁移率边的概念,即迁移率边以上的高能量电子表现出扩展性质,低能量电子表现出局域化性质.安德森局域化现象依赖于介质的维度,对于一维无序系统所有的态都是局域的.随着对无序系统的深入了解,研究发现无序系统中局域态的局域化长度以及波的传播受到其结构的种类影响[69].无序种类由无序谱表征,两个极端情况分别为有序系统和非关联无序系统,目前对于无序系统分类所使用的有序度量(order metric)的研究仍是一个开放的问题.尽管对于无序分类的度量及其影响无序系统中波传播行为的理论计算是个很复杂的问题,近些年来利用集成光学系统研究无序系统中的物理问题取得了一系列的进展,这得益于该系统的可操纵能力,可以对无序结构进行灵活设计.

早在1989 年就已经有理论预言光在无序系统中横向的局域化现象[75],直到2007 年以色列理工学院Segev 研究组[76]才首次在二维光子晶体结构中观察到这一现象(如图4(a)).他们利用光感应技术在10 mm 长铌酸锶钡光折变晶体(SBN:60)中诱导周期性的三角晶格式折射率分布,进一步在每个格点上加入随机扰动使得折射率以一定的无序度改变,另外结构中要保证无序是不随时间变化的,即沿传播方向折射率分布不变[76].2008 年Lahini等[44]在一维等间距的耦合光波导阵列(铝砷化镓波导)中也实验观察到了安德森局域化现象,描述该系统的哈密顿量可以用(2)式表示,实验中他们控制耦合波导之间间距不变,而每个波导的宽度在一定范围内随机变化(对角无序).他们理论预测并且实验观察到了局域态的传播,对于有限系统同时也存在扩展的本征态,而这些扩展态在无限系统下将是局域的,只是局域化长度会更大.早期这两项研究工作也都讨论了非线性效应对于安德森局域化的影响,他们发现非线性效应会增强局域化过程,这与更早之前非线性自聚焦效应导致的光孤子的结论相像[77].随后研究者也在波导间距随机变化(非对角无序)的飞秒激光直写玻璃光波导阵列中观察到了安德森局域化现象[78].光在不同无序度下的扩散过程也被广泛研究并被实验上观察到,如光在周期系统中的扩散是弹道式输运过程[13],在无序系统中表现出局域化特征[44,71,76],在一定无序度的结构中表现出扩散式过程[79](扩散速度介于前二者之间).安德森局域化要求势场是不随时间变化的,而对于无序含时的系统,Segev 研究组[80]发现波的输运表现出超传输(hyper-transport)现象,即扩散速度快于周期系统中的弹道式输运过程,并且动量空间谱宽也随时间扩展.近来,人们在无序铌酸锂光子晶体和硅光子晶体结构中也观察到了安德森局域化现象[81,82].

图4 (a) 二维无序光子晶格中的安德森局域化现象[76];(b) 一维准周期飞秒激光直写光波导阵列[85];(c) 飞秒激光直写螺旋式波导阵列结构实现Floquet 拓扑绝缘体[25];(d) 弯曲波导阵列实现等效磁场,模拟Aharonov-Bohm 效应[89];在耦合环腔阵列结构中产生(e) 拓扑绝缘体激光[90]、(f) 拓扑保护多光子量子光源[91];(g) 基于谷光子晶体结构设计等比分束器并实现双光子量子干涉[57];(h) 无序拓扑安德森绝缘体结构[92];(i) 基于一维SSH 模型在硅基结构中产生关联光子对[93];(j) “含时”哈密顿量系统用于研究拓扑泵浦[87];(k) 奇偶-时间对称与对称破缺交界面处局域的拓扑边界态[94];(l) 非厄米SSH 模型中非线性对奇偶-时间对称相变过程的影响[22]Fig.4.(a) Anderson localization in a two-dimensional photonic lattice[76];(b) simulation of one-dimensional quasicrystals in femtosecond-laser-written (FLW) optical waveguides[85];(c) realization of photonic Floquet topological insulators in a FLW helical waveguide array[25];(d) realization of an effective magnetic field and simulation of Aharonov-Bohm effect using curved waveguide arrays[89];generation of (e) topological insulator laser[90] and (f) multiphoton quantum source[91] in coupled resonator arrays;(g) design of a 1∶1 topological beam splitter in valley photonic crystals and realize the two-photon quantum interference[57];(h) photonic topological Anderson insulator[92];(i) generation of biphoton state in a SSH photonic lattice[93];(j) topological pumping in a system described by a time-varying Hamiltonian[87];(k) topological edge state in a photonic lattice at the interface between the structures with and without parity-time symmetry[94];(l) nonlinear tuning of PT symmetry and non-Hermitian topological states[22].

耦合光波导阵列系统灵活的可调控能力也被用来研究准周期晶格结构(介于周期系统与无序系统之间)中的物理.准周期系统缺少长程平移对称性,表现出准周期性(长程有序),其中两个典型的例子分别为Harper 模型和Fibonacci 模型.Harper模型是外加磁场的二维方格模型在一维模型上的投影,可以用来研究Hofstadter 蝴蝶能谱、拓扑边界态等[83].Harper 模型和Fibonacci 模型理论上具有相同的拓扑分类[84],随后实验上通过对局域边界态有无的观察证实了这一观点[85](如图4(b)所示).通过调制波导折射率和耦合系数的分布,研究者实验上分别实现了对角[86]和非对角[87]准周期一维光波导阵列,并在相应系统中观察到了局域-去局域化转变过程.另外,Segev 研究组[88]利用原先样品的制备技术在准周期系统中引入无序度,并且观察到了与周期系统不同的无序增强准周期系统输运过程的现象.

3.2 拓扑光子学

拓扑绝缘体是一类在材料体内绝缘,特定边界上表现出导体性质的结构.这一类结构具有一些优良的性质,如电子的鲁棒性传输,没有背向散射等[23,95].2016 年诺贝尔物理学奖颁给了David Thouless,Michael Kosterlitz 和Duncan Haldane 三位物理学家以奖励他们在拓扑相变方面的研究.拓扑绝缘体的研究起源于对于量子霍尔效应的拓展探索,即电子在二维周期晶格势场下外加电磁场的行为.Thouless 等[96]发现电子电导跟描述系统能带的常数有关(TKNN 数),系统的拓扑相由该拓扑数描述.在具有不同拓扑性质的域(domain)的边界上有局域的边界态,边界态的个数与两个域的拓扑数有关,即体边对应关系.拓扑相变不具备传统相变中的自发对称破缺过程,而是伴随着拓扑数的突然变化.2008 年,Haldane 和Raghu[97]从基本的麦克斯韦方程出发,理论提出在破坏时间反演对称性的光子晶体结构中也具备像电子系统中的拓扑边界态现象.随后2009 年Wang 等[98]在磁光子晶体中进行了实验验证,但相应材料体系的磁光系数较低,往往需要超强的磁场,这在实验上是比较难实现的.近些年来随着集成光学系统加工工艺的成熟,很多新奇的拓扑物理现象得以被实验实现.

拓扑相变过程要求系统的能带被打开,对于二维周期系统,需要通过破坏其时间反演对称性或者空间反转对称性来实现.前面提到的在周期晶格结构中外加磁场可以破坏时间反演对称性,而光学系统的磁效应比较弱难以实现拓扑能带,取而代之的是通过设计哈密顿量实现有效磁场,如周期性调制格点间跃迁概率、采用螺旋式波导阵列等.2013 年Rechtsman 等[25]提出利用螺旋形波导结构破坏时间反演对称性(z-reversal symmetry),他们利用飞秒激光直写技术制备如图4(c)所示的六角晶格光波导阵列,通过坐标变换将势场分布转换为不含时的分布,系统的哈密顿量可以表示为

等效规范势A(z)=k0RΩ[sin(Ωz),−cos(Ωz),0],Ω,R分别为螺旋波导的转弯频率和半径.紧束缚近似下,波函数的演化满足其中c是波导间耦合系数.由于哈密顿量耦合项是“含时”的,其本征态需要用Floquet 模式ψn=exp(iβz)ϕn(ϕn是关于z的周期函数)求解.对于螺旋形六角晶格结构,他们求解发现系统能带在狄拉克简并点打开,并且在带隙中存在方向性传输的拓扑边界态.由于拓扑边界态仅支持顺时针方向的模式,因此该系统中边界态的传播没有背向散射,并且对于边界上的缺陷或者无序的存在不敏感,他们进一步在实验上证实了这些结论.2014 年Longhi[99]提出通过线性调制光晶格中波导的传播常数来实现有效磁场,从而用于构建Aharonov-Bohm 笼子(AB cage,有效磁通量为 π).这一理论设计于2018年被Mukherjee 等[89]在飞秒激光直写光波导阵列中观察到.实验上他们采用图4(d)所示的弯曲式波导阵列结构,等效地使得传播常数线性变化.在加工每一根波导时沿着传播方向周期变化直写速度,使得传播常数“含时”变化,另外需要控制波导间距不变使得耦合系数近似恒为常数,系统的等效哈密顿量为

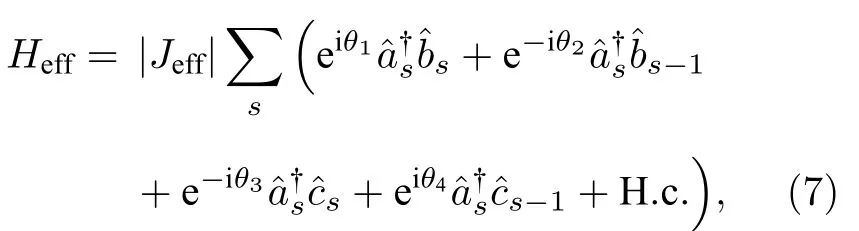
其中有效耦合系数Jeff是复数,分别表示粒子在第s个晶胞A,B,C三种格点上的产生(湮灭)算符.哈密顿量中的有效磁通量与周期调制传播常数的控制参数有关.实验上他们展示了磁通量为 π 时,分别在体内和边界上激发时光强的呼吸运动现象,边界态的呼吸频率要远低于体态的呼吸频率.值得一提的是,2018 年Keil 等提出通过在两个耦合波导中引入传播常数失谐的辅助波导也可以实现等效的 π 相位的耦合[100],他们进而以此构建了AB 笼子并且观察到了体态和边界态的呼吸运动现象[101].

在2.3 节中介绍的基于耦合环腔阵列的拓扑结构具有时间反演对称性,但是在考虑了赝自旋后,哈密顿量中则引入了等效磁场,对于两种赝自旋其边界模式的手性相反.在这些系统中,只要结构的缺陷或者无序大小不会引起两种赝自旋模式混合,单向的边界模式就能受到拓扑保护.这些模型近来也被应用于拓扑激光、量子信息的研究:2018 年Bandres 等[90]在磷砷化镓铟(InGaAsP)环腔阵列中实现拓扑绝缘体激光,他们发现在拓扑平庸环腔阵列中出射多模激光,而在拓扑结构中出射单模激光(如图4(e)所示),并且在拓扑结构中产生的激光可以沿着边界传播,不受结构缺陷的影响,他们采用的环腔阵列结构基于图2(a)所示的量子自旋霍尔系统.同年Mittal 等[102]基于硅四波混频效应在类似的结构中(硅环腔阵列)实现了关联光子对的产生,并且发现当泵浦光、信号光和闲频光与边界模式的频率一致时,光子对的产生概率增强.随后2021 年Mittal 等[103]基于反常量子霍尔模型以及双泵浦技术在硅环腔阵列中产生频率可调光子对,产生的光子对具有能量-时间纠缠特性,并用于量子干涉实验.2022 年Dai 等[91]基于Floquet 拓扑绝缘体结构在硅环腔阵列中产生多光子纠缠态(如图4(f)所示),并且测量了在有无缺陷的结构中产生的纠缠态的保真度,从而证明了产生的Einstein-Podolsky-Rosen 态受到了拓扑保护.

除了前面提到的具有时间反演对称性的耦合环腔阵列系统,研究发现在光子晶体中通过破坏系统的空间反转对称性也可以产生拓扑绝缘体结构.2007 年,牛谦研究组[104]设计石墨烯六角晶格结构使得两个亚晶格格点能量不同,从而破坏空间反转对称性.他们发现该系统支持一对具有固有磁矩的赝自旋模式,并且与能带中能谷的位置有关(狄拉克简并点).他们进一步提出在外加电场下,不同能谷位置的载流子将沿着相反的方向传输,即能谷霍尔效应.基于这一模型,2013 年Khanikaev 等[105]在六角光子晶格结构中观察到了边界态传输,对于两个相反的赝自旋态激发条件下光子的传播方向相反.他们实验上也证实了当结构中的缺陷或无序大小不引起两个能谷的边界态模式混合时,边界态的传播受到拓扑保护.随后这种能谷霍尔拓扑绝缘体结构也被拓展到近红外波段,如飞秒激光直写光波导阵列[106]、硅光子晶体结构[107,108].近来谷光子晶体中的拓扑保护边界态也被用到量子信息领域:2018 年Barik 等[109]在中心具有外延生长的InAs量子点的GaAs 谷光子晶体结构中观察到了量子单光子源不同圆偏振模式的方向性发射.2021 年任希锋研究组与董建文研究组在[57]硅能谷光子晶体结构中基于谷霍尔效应设计等比分束器结构(如图4(g)所示),并在该结构中实现了量子干涉过程.谷光子晶体中的这类边界模式也被用于实现拓扑激光[110],由于此设计基于光子晶体结构,因此结构尺寸比耦合环腔阵列系统更加集成化.

值得一提的是,2018 年Stutzer 等[92]利用扭曲的六角晶格结构的波导阵列实现了光拓扑安德森绝缘体模型.实验上他们通过控制光入射到一维等间距波导阵列的角度来控制耦合进二维六角晶格波导阵列中的能量大小,从而实现处于带隙中心的模式的激发(如图4(h)所示).他们在破坏空间反演对称性的基础上改变子晶格中两个格点的能量(折射率)来破坏空间反转对称性,使得系统能带从拓扑相转变到平庸相,实验表现为观察不到边界态模式的激发.他们进一步又对每个格点的能量分布引入无序度(通过改变加工波导所使用的飞秒激光的扫描速度来改变折射率),系统能带又转变为拓扑能带,实验上观察到了手形边界态的方向性传播.

对于一维系统,产生拓扑相要求系统具有某种对称性,其中一个典型的例子是基于聚乙炔结构的Su-Schrieffer-Heeger(SSH)模型.SSH 模型具有手性对称性,系统的哈密顿量可以表示为[111]

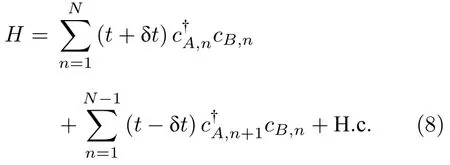
除了上述拓扑模型,耦合光波导阵列系统可用于构造“含时”哈密顿量来实现拓扑泵浦.在这一类系统中,通过绝热改变系统的某个参数能够实现拓扑边界态的绝热演化,即从其中一个边界态绝热演化到另一个边界态,而不需要边界态之间的耦合.2012 年Kraus 等[87]在铝砷化镓(AlGaAs)和飞秒激光直写玻璃光波导中分别研究了准晶结构中的拓扑边界态及其拓扑泵浦现象.用于研究拓扑泵浦的结构如图4(j)所示,系统的哈密顿量可表示为

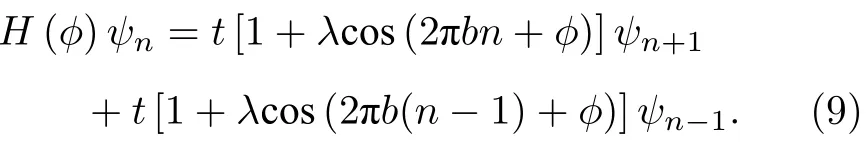
其中波导之间的耦合系数按照准周期分布,而控制绝热泵浦的参数ϕ沿着波导传播方向(z轴)缓慢变化.他们研究发现二维整数量子霍尔系统的哈密顿量在考虑其中一个方向的周期性后,与之对应的动量k与绝热泵浦参数有关(k=ϕa,a为晶格常数),因此通过扫描参数ϕ可以实现拓扑边界态在动量空间的绝热演化.实验上他们观察到了光从阵列格点的一端穿过格点绝热演化到另一端的现象.近几年“含时”变化的波导阵列结构也被用来研究合成维度拓扑绝缘体[120]、四维量子霍尔效应[121]、Thouless 泵浦[122,123]等物理现象.

3.3 非线性和非厄米系统

光在非线性介质中的传播存在群速度色散以及自相位调制效应,可以产生超短脉冲或者光孤子.非线性光波导阵列中的光孤子现象在1988 年被首次提出[124],1998 年在铝砷化镓光波导阵列中实验观察到[77],随后2003 年在二维光折变SBN光子晶格中也观察到了非线性光孤子现象[125].描述这一类系统的哈密顿量为[124]

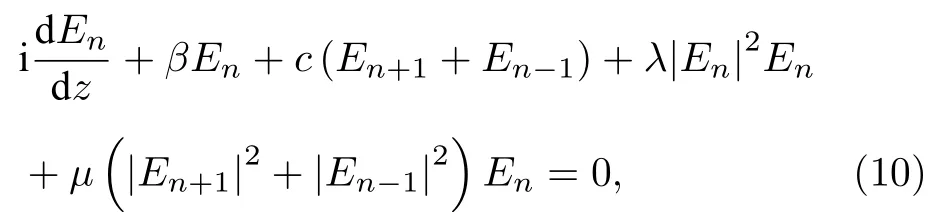
其中En表示第n个格点处的电场强度,c表示粒子在相邻波导间的跃迁概率.非线性项描述了第n个波导中的自相位调制,最后一项表示了相邻波导的非线性重叠作用.通常自相位调制起主导作用,最后一项被省略.早些年有大量的关于光波导阵列中光孤子的理论和实验研究工作[77,125,126].非线性导致光局域化增强的现象很容易让人联想到拓扑绝缘体中局域的边界态,近些年开始研究非线性效应对于拓扑结构的拓扑相和拓扑边界态的影响[127]: 2018 年Dobrykh 等[128]在微波环腔阵列中研究SSH 模型拓扑边界态的非线性调谐,他们发现随着泵浦功率的增大,电磁场更加局域在边界处,并且观察到了非线性蓝移现象;2020 年Szameit研究组[26]利用飞秒激光直写光波导系统实验观察到光Floquet 拓扑绝缘体中的孤子现象[21],随后他们又发现非线性效应可以改变系统能带拓扑性质,从而使得原本拓扑平庸的结构在非线性作用下转变为拓扑绝缘体.

上述讨论的物理模型中描述系统的哈密顿量是厄米的,即满足能量守恒定律.而在真实的物理体系中,系统与外界环境之间往往存在耦合,有效非厄米哈密顿量近似是目前处理这一问题普遍采用的方法[129].非厄米系统中一个有趣的现象是当系统满足奇偶-时间对称性(PT 对称)时,系统表现出与厄米系统一样的实数能谱.通过调制哈密顿量非厄米项的大小,系统可以从PT 对称未破缺相转变到PT 对称破缺相.系统处在PT 对称破缺相时,能谱不再是实数分布,本征函数不再组成正交基.非厄米系统表现出许多新奇的物理现象,如趋肤效应、光漏斗效应等[130,131].集成光学系统在一定程度上可以实现光增益或损耗,近些年来被用于实现非厄米系统的量子模拟: 2010 年Rüter 等[132]基于掺铁铌酸锂材料研究光在具有PT 对称的非厄米耦合波导结构中的传播,他们利用材料中的光折变非线性效应在其中一根波导中引入光学增益,实验上观察到了非互易的光的传输,即改变输入端口后输出端光强分布发生变化.2017 年Szameit研究组[94]利用图4(k)所示的扭曲的飞秒激光直写光波导阵列结构实现了非厄米SSH 模型的模拟,他们研究了该系统中PT 对称未破缺-破缺相转变过程与SSH 模型二聚作用大小(dimerization)的关系,最终实验上观察到了两个不同PT 对称拓扑相的交界面上存在局域的边界态.2021 年陈志刚研究组[22]利用图4(l)所示的分段式波导阵列结构实现非线性非厄米SSH 模型的模拟,他们理论研究了非线性项以及非厄米项对于系统能谱和本征态的影响,并提出通过判断波导阵列中光流向有损或有增益的波导的方式来判断非线性作用是否破坏了系统的PT 对称性.实验上他们使用弱相干光在偏置光折变晶体(SBN:61)中写入这种带有损耗的分段式结构(折射率改变可以维持1 h 以上),通过控制在界面缺陷波导处输入的偏置场的方向来实现自聚焦和自散焦非线性效应,在实验上观察到了PT 对称系统转变为PT 对称破缺的系统.另外非厄米系统的模拟也在光子晶体和环腔结构中得以实现[133].

4 数字型量子模拟

2.4节介绍了矩形多端口干涉仪,它的简化版本(MZ 干涉仪替换为等比分束器加相移器)被用于模拟可实现通用量子计算的离散量子随机行走模型,干涉仪网络中的分束器相当于同时实现了经典随机行走的抛硬币操作(coin operator)和平移操作(shift operator).2012 年Osellame 研究组[12]利用飞秒激光直写系统制备离散型量子随机行走芯片,他们通过输入双光子偏振纠缠态表示水平/竖直偏振),测量输出端口双光子的分布实验展示了玻色子(费米子)的聚束(反聚束)特征.2013 年他们又利用该系统制备了无序分布的离散型量子随机行走线路[14],通过改变波导的相对长度使得光子在两个行走方向的其中一臂引入随机相位,从而在无序离散型量子随机行走芯片中观察到了安德森局域化现象,并观察到了偏振纠缠光子对的局域化现象(如图3(b)所示).2017 年Pitsios 等[134]利用激光直写技术制备级联芯片模拟自旋链淬火后的纠缠增长过程,其中第1 个芯片通过双光子离散型量子随机行走过程模拟5 个格点的自旋链上的演化过程,第2 个芯片上的热光相移器用于测量输出模式的纠缠度.

玻色取样问题研究的是n个不可区分的单光子输入到m(m>n)模式干涉仪中输出端光子数的分布,这一问题的求解对于经典计算机而言是#P-hard 问题.对于一些特定的取样问题,基于这一模型近些年来在超导系统和光学系统中展示出了量子优越性[135−137].在集成光学系统中,2013 年同年有3 篇研究工作分别在飞秒激光直写光波导以及SOI 波导系统中实验实现了玻色取样(光子数为3,最多6 个光学模式)[15−17],2019 年Paesani等[138]在同一个硅芯片上实现了标准玻色取样、散射玻色取样,以及高斯玻色取样(8 光子,12 个光学模式),关于玻色取样的具体的介绍可以查阅文献[139].

另外基于多端口干涉仪的集成光学芯片也被用来量子化学模拟,如在硅基光芯片上利用量子相位估计以及变分本征值求解法求解分子基态能量[138,140].对于具有n个量子比特的量子态,描述系统演化的哈密顿量的维度为 2n×2n,在量子化学中系统的哈密顿量H可以表示成关于系统尺寸具有多项式个数的泡利矩阵叠加的形式.因此,对于给定量子态 |ψ〉,算符H的期望值可以拆分成多个泡利算符期望值的线性叠加[141],泡利算符及其张量积的期望值可以通过对每个量子比特的局部测量得到.对于矩阵H的本征值求解问题,其最小本征值对应的本征态将使得Rayleigh-Ritz 商数最小,因而可以归结为变分问题.基于这种思想,量子变分本征值求解法可以用于分子基态能量的求解: 首先制备初始量子态,利用量子期望值测量估计待测哈密顿量的期望值,进一步计算Rayleigh-Ritz 商数,根据得到的商的大小反馈回初始态制备过程,循环往复使得Rayleigh-Ritz 商数最小.在2014 年Peruzzo 等[140]考虑He-H+分子的哈密顿量可以表示成:

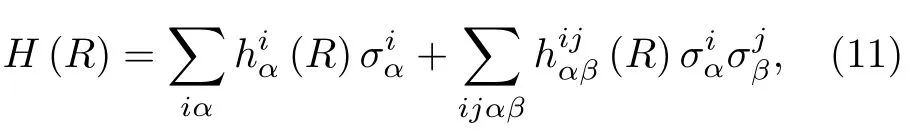
其中R表示核间距,表示子系统i中的泡利算符(i=x,y,z),展开系数h是实数.实验中他们在硅基芯片上通过热调相移器和干涉仪的结构完成初始量子态的制备以及期望值的测量.将输出端符合计数的测量结果发送至经典处理单元,进一步反馈到初态制备的量子线路中,最终经过多次迭代可以得到不同核间距下He-H+分子的基态能量.2017年Paesani 等[138]利用贝叶斯估计在硅基芯片上模拟氢分子基态能量,他们的设计思想是基于贝叶斯量子相位估计算法[142]: 对于给定的哈密顿量H,其本征矢量 |ψ〉所对应的相位为ϕ.首先假定要估计的相位ϕ满足高斯分布P(ϕ) (先验条件概率),基于贝叶斯定理根据量子态经过幺正变换以及泡利Z算符后的测量结果来计算相位ϕ的后验概率分布,然后将先验概率分布替换为后验概率分布,通过多次迭代提高相位估计的置信度.实验上他们在硅基芯片上利用干涉仪以及热调相移器完成初始态制备以及控制幺正操作,氢气分子哈密顿量的本征态则利用Jordan-Wigner 变换转化到量子比特基矢,进一步他们在硅基芯片上模拟了不同原子间距下的氢分子键能[138].2018 年Sparrow 等[27]利用可编程的三角形结构的干涉仪结构模拟了分子振动模式的动力学演化,他们首先将分子中集体的振动模式分解成多个局域的振动模式的叠加,这些局域的振动模式对应于芯片中不同的路径,振动模式的演化则利用可实现任意幺正变换的干涉仪结构实现,实验上改变不同的输入态模拟了分子中不同振动模式之间的振荡、能量转移以及振动弛豫等过程.

5 总结和展望

本文总结了集成光学芯片上实现不同种类的量子模拟的研究进展,首先介绍了几种常用光学体系用于实现量子模拟的基本物理原理,然后基于不同的实验平台介绍了集成光学芯片的几种用途: 实现无序系统、拓扑绝缘体结构、非线性和非厄米系统的量子模拟,实现离散型量子随机行走、玻色取样模型,以及模拟量子化学中的分子能谱等.其中飞秒激光直写光波导系统可以对波导折射率以及空间构型做灵活的调制,在相应的结构上观察到了无序系统安德森局域化现象,利用“含时”波导阵列结构可以实现周期驱动Floquet 拓扑绝缘体结构、合成规范场、拓扑泵浦等结构的量子模拟;耦合环腔阵列系统由格点环腔和连接波导组成,通过调节连接波导中引入的相位或调节环腔之间耦合的透过率可以用于模拟量子自旋霍尔效应、反常量子霍尔效应以及Floquet 拓扑绝缘体,进一步结合硅基系统中的四波混频效应可以用于产生具有拓扑保护的量子光源;光子晶体结构具有更加集成化的尺寸,通过破坏体系的空间反转对称性可以实现谷霍尔效应,从而在平面内对光实现大角度的无散射弯折;在线性物理模型中加入非线性效应可以引起结构能带的变化,如使周期系统从拓扑平庸相转变到拓扑相、使非厄米系统从PT 对称相转变到PT 对称破缺相,这些新物理现象的实现需要用到如铌酸锂、铝砷化镓、磷砷化镓铟、铌酸锶钡光折变晶体等非线性光学材料;另外,基于硅基的多端口干涉仪结构具有很强的可重构能力、成熟的加工工艺,并且能够产生片上量子光源,实现任意的幺正变换,被用于实现离散型量子随机行走过程,玻色取样以及分子能谱的研究.

限于篇幅,其他一些在集成光学芯片上有趣的实验进展没有涉及,如利用线性调制波导阵列中单根波导的传播常数来模拟周期系统中的电子在外加力作用下的布洛赫振荡或者Zener 隧穿效应[143−145],通过调节波导间距来研究量子系统中的耗散问题[146]、分形结构中的量子输运过程[147]、六角图上的快速到达问题[148]等,另外还有实现如高阶拓扑绝缘体[149]、非阿贝尔几何相[150,151]量子模拟等.

集成光学系统不同的材料平台能够发挥不同的优势,从而用于实现某些特定任务的量子模拟.关于不同研究领域的交叉往往能催生出新物理原理或者新技术的突破,如关于非厄米、非线性以及拓扑绝缘体结构的研究催生了拓扑激光这种未来可能有实用化前景的技术.新奇的拓扑结构应用到量子信息领域有可能可以解决制备量子光源中频率稳定性的问题,而基于集成光学芯片系统结合机器学习算法有可能进一步推动新物理结构量子模拟和更加实际化用途的实现.另外,需要指出的是利用集成光芯片实现量子模拟也会面临一些挑战,如需要尽可能的提升系统的可扩展性、可操纵能力.为了实现量子优越性展示或其他特定的实际应用,多比特、大规模、复杂系统量子模拟将成为未来的发展趋势.在实验技术层面上,大规模的集成光学系统将面临着损耗、测量技术、实验成本等方面的问题,通过尝试新材料或者开发新技术,结合多种材料体系的优势或许可以解决一些关键难题.复杂系统的量子模拟同样要求理论方面的同步推进,反过来实验上对于未知物理现象的观察同时也能进一步完善描述复杂物理系统的理论.