基于GMS和改进最佳缝合线的视差图像拼接算法

李四杰，唐清善，高英华

(1.长沙理工大学物理与电子科学学院，湖南 长沙 410114; 2.中国人民解放军第3303工厂，湖北 武汉 430200)

0 引 言

图像拼接是指将多幅具有一定重叠区域的图像融合成一幅完整的大视角图像[1-4]的技术。图像拼接是计算机图像学领域的一大研究热点，在虚拟现实[5]、远程视频监控[6]、医学图像处理[7]、遥感技术[8-9]等方面都有着广泛而迫切的应用需求。

现有图像拼接算法主要可以分为3类：

1)全局对齐方法。

这类方法首先通过特征提取算法SIFT[10]或SURF[11]进行图像匹配，然后利用随机抽样一致(RANdom SAmple Consensus, RANSAC)算法计算出全局单应性矩阵进行图像配准，最后对图像进行融合得到无缝的拼接图像，如自动拼接(AutoStitch)算法[12]。文献[13]提出基于改进SURF的图像拼接算法，提高了图像匹配的效率。然而在大视差图像拼接的场景中，SIFT、SURF和其改进算法容易产生错误的匹配点，难以计算出精确的全局单应性模型，导致拼接图像出现鬼影和模糊等问题。

2)以尽可能投影(As-Projective-As-Possible, APAP)算法[14]为代表的空域变化绘制方法。

该类方法将图像划分为密集网格，对于每个网格分别计算出单应性矩阵进行对齐，即局部单应性，因此该方法对齐图像的效果很好，在视差较小的情况下表现优异，但计算量较大，并且会出现局部图像结构扭曲的现象。文献[15]提出了自适应尽可能自然(Adaptive-As-Natural-As-Possible, AANAP)算法，与APAP算法不同，该算法结合全局变换和局部变换进行拼接，局部变换用于对齐图像，全局变换用于矫正形状，避免了图像的局部扭曲，但是同样只适用于小视差的场景。文献[16]提出基于直线特征约束网格变形的图像拼接方法，该方法通过直线约束改善了图像非重叠区域的扭曲问题，同时提高了图像拼接的精度和还原度，在航拍图像拼接上效果较好。

3)基于缝合线的方法。

这类方法通过计算图像重叠区域上的最佳缝合线来拼接图像。文献[17]采用基于图像的颜色差异和几何差异的动态规划求解最佳缝合线。但该方法无法彻底消除鬼影问题，且在图像曝光差异大的情况拼缝较明显。

综上所述，在拼接图象视差较大的情况下，上述算法均无法解决鬼影、亮度不均等问题。因此，本文提出一种基于GMS和改进最佳缝合线的视差图像拼接算法。算法开始基于GMS算法快速获得图像中的特征匹配点，后通过改进最佳缝合线算法中的能量函数优化鬼影问题，再利用梯度域融合平滑图像中亮度不均匀区域，从而实现图像拼接。

1 基于GMS和改进最佳缝合线的视差图像拼接

Step1利用ORB算法在2幅输入图像中提取出大量的特征点，并计算特征描述子，通过暴力匹配(Brute Force, BF)算法，对2幅输入图像进行粗匹配，再由GMS算法过滤掉误匹配点。

Step2计算2幅图像之间的单应性矩阵，利用单应性矩阵将一幅图像投影到另一幅图像的平面上，得到配准图像。

Step3计算改进后的能量函数，并在配准图像的重叠区域利用图割求解最佳缝合线。

Step4在图像中缝合线两侧进行梯度融合得到输出图像。

本文算法主要流程如图1所示。

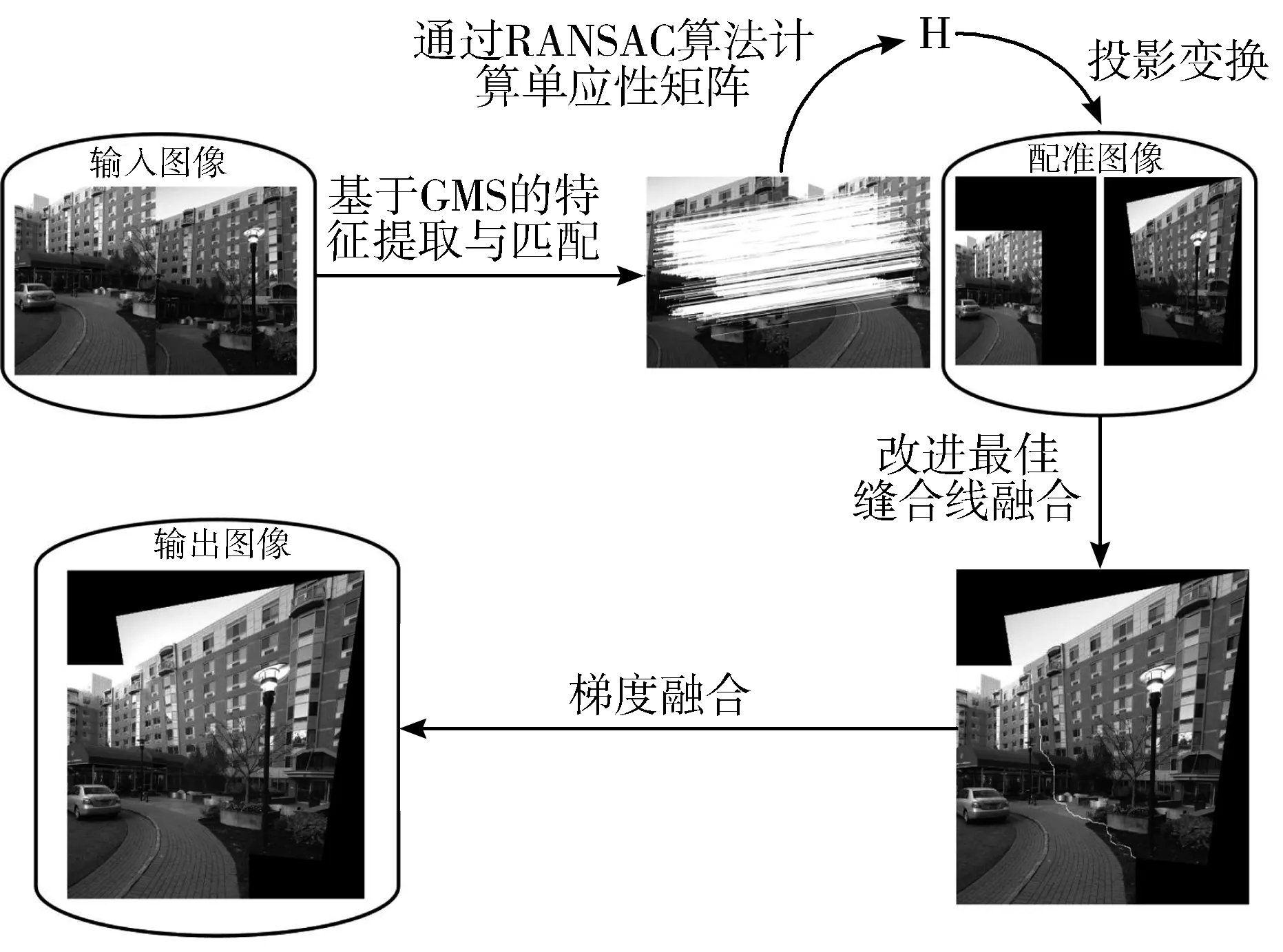
图1 基于GMS和改进最佳缝合线的视差图像拼接算法流程图

1.1 基于网格运动统计的特征匹配

特征点提取中的ORB算法特点是提取速度快、特征点鲁棒性差，易产生大量的误匹配点。而GMS算法将运动平滑度表示为区域中一定数量的匹配项的统计似然性[18]，即正确的匹配点周围一定会存在足够多数量的正确匹配点支撑它，而错误的匹配点周围没有或者只有极少数的匹配点，通过统计特征点周围的支持量可以快速地找到2幅图像中正确的特征匹配对。融合二者的优点，新的算法可以有效降低误匹配点，并保证特征提取的实时性。

在使用ORB算法和BF算法后，得到特征粗匹配对。接着应用GMS算法时，假设IA和IB为2幅输入图像，存在IA到IB最近邻匹配集合λ={λ1,λ2,…,λi,…,λN},其中λi表示一个特征匹配对。假设λi邻域支持量为Si，则有：

Si=|γ|-1

(1)

其中，γ是λ的子集，|γ|表示γ中包含特征匹配对的数量，-1项表示除去初始匹配对。

由于每个特征点是相互独立的，所以特征点邻域内支持量Si近似服从于二项分布，则有：

(2)

其中，Pt为2幅图像的2个对应区域内，在一个点匹配正确的条件下，周围点支持它的概率，Pf表示为2幅图像的2个对应区域内，在一个点匹配错误的条件下，周围点支持它的概率。R表示与所在网格区域相邻但不相交的网格数，n表示该网格中的特征点数。

Si的均值与标准差可由公式(3)计算：

(3)

根据标准差Sf与均值mf可以得出判断邻域特征支持量是否匹配正确的阈值：

τ=mf+αSf

(4)

通过实验可以发现mf的值小到可以忽略不计，而α通常取一个较大的值来保证可以筛除掉错误匹配，本文中α的取值为6。因此，τ也可以近似表示为：

(5)

其中，ns表示9个网格中特征点数量之和的平均值。

将图像IA和IB分别划分为G个网格，取G=20×20。统计网格中所有特征匹配对的邻域支持量Si，并删除Si<τ的特征匹配对，剩余的特征匹配对即为正确匹配。

1.2 单应性变换模型

在完成图像匹配之后，通过RANSAC算法找到至少4对匹配点，可以计算出单应性矩阵H。接着利用单应性矩阵H将2幅图像变换到同一坐标系上。

(6)

其中,(x,y)和(x′,y′)分别为变换前后的图像坐标。其中h0、h1、h3、h4描述了图像的尺度变化和旋转量；h2表示水平方向的平移量；h5表示垂直方向的平移量；h6、h7表示水平和垂直方向的变形量。

1.3 基于图切割的最佳缝合线算法的改进

经过配准后可以得到配准图像I0和I1，用P表示I0和I1的重叠区域，令L={0,1}表示一个标签集合，其中“0”代表该像素点属于图像I0，“1”代表该像素点属于图像I1。对于重叠区域中的每一个像素p赋予标签lp∈L，即求得重叠区域的缝合线l。缝合线l的能量函数表示如下：

(7)

其中，N⊂P×P是相邻像素对(p,q)的四邻域像素集合。

能量函数由2个部分组成：1)数据项，表示把标签lp赋给像素点p的惩罚，用Dp(lp)表示；2)平滑项Sp,q(lp,lq)，表示把标签对(lp,lq)赋给相邻像素对(p,q)的惩罚。

最佳缝合线即所含能量最小的缝合线，能量最小问题可以由图切割法求解[19]。相比动态规划法，图切割法更加灵活。图切割法首先需要建立一个有向图G=<Φ,Ψ>，其中Φ表示顶点的集合，而Ψ表示有权边e的集合。另外还有2个特殊的顶点，分别称为源节点和汇节点。图像的一个割C实际上就是Ψ的一个子集，即C⊂Ψ。经过图切割之后得到的有向图G=<Φ,ψ/C>源节点和汇节点是分离的，也就是说源节点和汇节点之间不存在通路。定义成本函数|C|为图像的割所经过有权边e的权值之和。即：

(8)

其中，we为每条边的权值。

如图2所示，假设基准图像和待拼接图像的重叠区域为一个3×3的像素矩阵，利用图切割求解最佳缝合线的具体步骤如下：

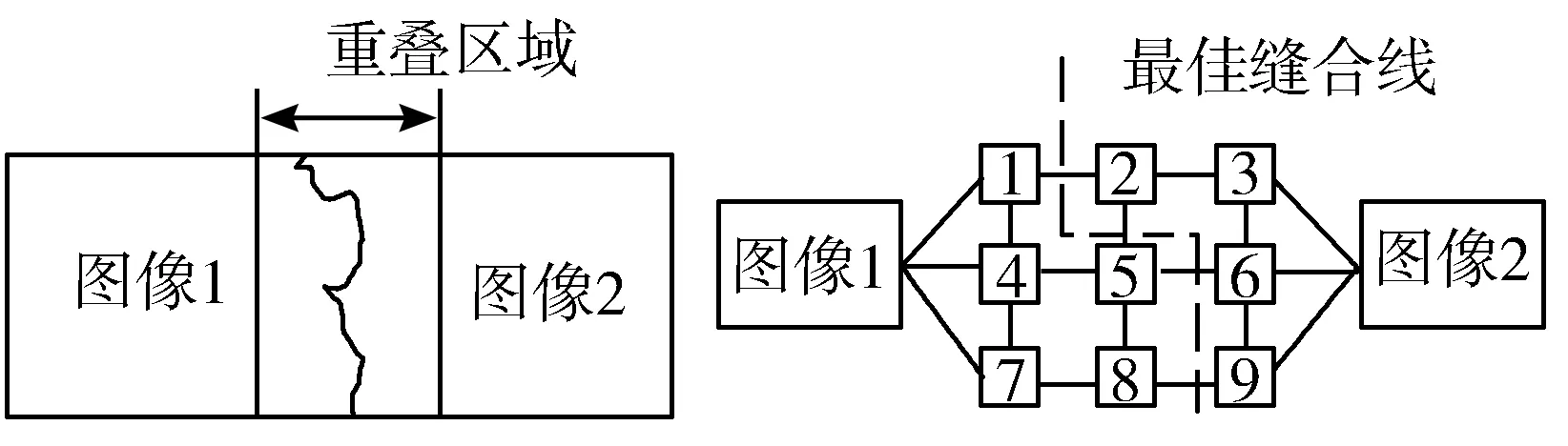
图2 最佳缝合线示意图

Step1在重叠区域上建立图。重叠区域上的每一个像素点对应图的一个节点，像素点之间的连线对应图的边，边的权值为连线两端像素的颜色差。源节点和汇节点分别代表基准图像和待拼接图像。

Step2计算数据项和平滑项。

数据项的定义为：

(9)

其中，∂Ik∩∂P分别表示Ik(k=0,1)与P的公共边界。

当像素点被赋值了错误的标签时，会使得该数据项的值趋向于无穷大，这样可以避免所求最佳缝合线穿过2幅图像重叠区域的边界。

平滑项的定义为：

(10)

I*(·)=‖I0(·)-I1(·)‖2

(11)

其中，I*(·)表示用欧氏距离计算2幅图像之间的RGB颜色空间距离差。

Step3利用最大流算法进行迭代求取最小能量，源节点扩张方式选择α扩张[20-21]。求取使得目标能量函数最小的缝合线，即最佳缝合线。

图2中的虚线表示最佳缝合线，最佳缝合线左边的像素1、4、5、7、8来自于基准图像，而右边的像素2、3、6、9则来自于待拼接图像。

人眼对于RGB颜色空间中3个颜色分量敏感程度是不相同的[22]，HSV颜色空间在图像处理中使用较多，相比RGB有着更符合人类视觉的颜色表达能力[23]。因此，本文采用HSV颜色空间，并且在约束项中添加图像的梯度信息来改进最佳缝合线的能量函数。

改进算法的步骤1和步骤3与上述Step1和Step3保持一致，改进算法主要对能量函数公式(7)中的平滑项进行了修改。

1)HSV颜色差异项Ehsv。

由于RGB空间3个分量均对图像亮度高度敏感，即图像亮度改变，3个分量都会受到亮度的影响而改变。这导致拼接图像在亮度变化不大的区域会产生不自然的切缝。改进算法将HSV颜色空间引入到最佳缝合线算法中，使最佳缝合线不仅对图像的亮度敏感，而且图像的饱和度以及明度都会影响最佳缝合线求解的结果。Ehsv的定义如下：

(12)

(13)

其中，h、s、v分别为HSV颜色空间的3个分量：色调(H)，饱和度(S)，明度(V)。

2)梯度差异项Eg。

对于彩色图像来说，图像梯度反映的是像素邻域内颜色的变化，图像边缘像素值变化大，所以在图像边缘有较大的梯度值，而图像中较平滑的部分梯度值则较小。将图像的梯度差异项加入缝合线搜索的约束项中，使缝合线避免穿过图像中物体的边缘。

Eg=‖∇I0(p)-∇I1(p)‖2+‖∇I0(q)-∇I1(q)‖2

(14)

其中，∇I0(p)表示图像I0在像素点p处的颜色梯度值，可由RGB图像与Sobel算子进行卷积求得。

综上，改进后的能量函数为：

(15)

(16)

其中，ε为2项之间的可调节的比例因子，ε的值越大，代表能量函数受Ehsv项的影响越大。

1.4 梯度融合

由于存在曝光差异，即使在利用最佳缝合线融合图像后，图像的拼缝仍然存在。本文采用梯度融合的方法对拼接图像进行进一步的优化。梯度融合即在梯度域中平滑过渡图像拼缝来提高融合图像的质量[24]。具体步骤如下：

Step1根据求解最佳缝合线过程中得到的掩膜，将配准后的图像I0和I1分别与掩膜进行点乘，得到拼接图像f(x,y)，计算f(x,y)的梯度(Gx,Gy)。

Step2计算f(x,y)的散度div(G)，并以散度向量作为导向向量构建泊松方程：

∇2f(x,y)=div(G)

(17)

其中：

Step3添加边界约束条件：

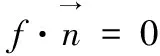
(18)

Step4将最佳缝合线两端的梯度值以及边界上的梯度值设置为0，利用牛顿迭代法可求解方程(17)，求得的解即为融合后的图像。

2 实验结果与分析

为了验证本文算法的效果，本文在Win 10系统的PC上进行算法仿真实验，处理器为Intel(R) Core(TM) i5-9300H CPU @ 2.40 GHz。分别从图像匹配质量和拼接质量2个方面评估算法的性能。

2.1 图像匹配实验

如图3(a)所示，从上至下分别为4组分辨率为600×480的实验图像，图3(b)～图3(d)为实验结果。从图中可以看出每组的左右图像之间存在较大的视差，这为图像特征匹配带来一定的挑战。防止特征点过少导致的图像配准失败，实验中SIFT算法和SURF算法都设置了比较低的阈值来获取更多的特征点。由表1可以看出，受到视差的影响，SIFT算法和SURF算法匹配的结果中存在大量的误匹配，而本文算法匹配的正确率远大于上面2种算法，匹配质量更加可靠。另外，本文算法具有更快的剔除误匹配的速度，保证了算法执行的效率。

图3 图像匹配结果对比图

表1 3种特征匹配算法对比

2.2 图像拼接实验

2.2.1 参数ε选取

从图4中可以看出，ε的不同取值会直接影响最佳缝合线的走向。如图4(c)～图4(e)中标记的方框所示，当ε的值为0.75、0.83、1时，最后的拼接图中都生成了明显的路标鬼影。而当ε取0.5和0.66时，得到的最佳缝合线基本一致，生成的拼接图像也无明显的畸变。为了保持能量函数中的Ehsv项所占权值大于Eg项，下面的实验中均取ε=0.66。

(a) ε=0.5 (b) ε=0.66

(c) ε=0.75 (d) ε=0.83

(e) ε=1

2.2.2 图像拼接主观评价实验

为了验证本文算法生成拼接图像的质量，选取2组分辨率分别为800×541和640×480的视差图像，然后将本文算法分别与AutoStitch算法、APAP算法、AANAP算法，以及最佳缝合线算法进行对比实验。

从图5和图6可以看出，对于视差图像的拼接，除本文算法以外，其他算法生成的拼接图像均出现了“鬼影”。同时在图5(d)中APAP算法的结果图出现了严重局部图像扭曲的问题，图6(d)和图6(e)出现了明显的亮度不均匀。而本文算法在2组对比实验中均表现良好，无明显瑕疵，且生成的拼接图观感上比较自然。

对于传统的最佳缝合线算法，由于其采用基于RGB颜色空间的欧氏距离差定义平滑项，仅仅只能保持局部颜色相似，而在某些图像结构比较复杂的情况下，求得的最佳缝合线有时候不符合人类视觉。如图5(f)所示，图像的背景为颜色相似的天空，传统最佳缝合线仅考虑了RGB颜色差异，导致在拼接图像中的黑色方框处出现了明显的桅杆鬼影。而本文算法由于考虑了图像的梯度差，使得最佳缝合线倾向于沿着物体的边缘，避免直接穿过桅杆，消除了鬼影。在图6(f)中的黑色方框处，传统的最佳缝合线算法所求缝合线穿过了公路的边沿处，导致拼接图像出现断层。而本文算法所求最佳缝合线避开了路沿和减速带，使拼接图像较为自然。

(a)船舶图1

(b) 船舶图2

(c) AutoStitch

(d) APAP

(e) AANAP

(f) 最佳缝合线

(g) 本文算法

(a)公路图1

(b) 公路图2

(c) AutoStitch

(e) AANAP

(f) 最佳缝合线

(g) 本文算法

2.2.3 图像拼接自然度评价实验

为了更直观地评价各算法拼接图像的自然度，本文采取图像自然度评价算法[25](Natural Image Quality Evaluator, NIQE)对拼接图像的质量进行评价。NIQE是一种无参考图像技术指标，该算法不需要输入任何的参考图像信息，就能够独立地对被测图像进行打分。由于人类视觉系统总是倾向从图像中清晰的区域对图像的质量进行判断[26]，因此NIQE算法首先在被测图像中提取感兴趣区域，接着从这些区域上计算36个相同的自然场景统计指标，然后将指标与多元高斯模型进行拟合。最后，通过公式(19)计算待测图像与自然图像所建立的模型参数之间的距离来评估图像质量。NIQE的值越小代表图像的自然度越高，即拼接图像的质量越好。反之，NIQE的值越大说明图像的自然度越低，图像失真越严重。

(19)

其中，ν1、ν2、Σ1、Σ2分别代表自然图像多元高斯模型和被测图像多元高斯模型的均值向量和协方差矩阵。

利用NQIE算法对图像拼接对比实验1和对比实验2中5种拼接算法所生成的拼接图像分别进行打分，如表2所示，本文算法在2组实验中的得分均低于AutoStitch、APAP算法、AANAP以及最佳缝合线算法，这表明本文算法拼接图像的自然度优于上述4种算法。

表2 5种拼接算法NIQE得分

3 结束语

针对视差图像拼接时易出现鬼影和亮度不均等问题，本文提出了一种改进的图像拼接算法。在图像配准阶段，结合ORB算法和GMS算法获取可靠的特征点，从而得到更精确的变换模型，提高了图像配准的鲁棒性。在图像拼接阶段，将HSV颜色空间和图像梯度差引入能量函数中改进最佳缝合线，使鬼影问题得到优化；同时采用梯度融合平滑拼接缝两侧亮度，使拼接图像整体上看起来更自然。通过2组对比实验对本文算法的性能进行了评估，结果表明：对于视差图像场景的图像拼接，本文算法的拼接效果优于AutoStitch、APAP、AANAP和最佳缝合线算法，特征点匹配正确率最高提升了4.73倍，图像拼接自然度平均提升了22.6%。在进一步的研究工作中将把算法移植到硬件平台上进行加速，更好地提高算法的实时性。