面向带时间窗车辆路径问题的PGSA算法优化
王 阔,郝福珍
(华北计算技术研究所,北京 100080)
0 引 言
随着现代社会的发展,物流场景下的路径规划问题的重要性也越来越凸显出来,自从1959年被Dantzig等[1]提出以后,就引起了人们广泛的关注[2-3]。该类问题的存在对于人类在实际场景中应用先进的计算机技术、合理调度与规划物流车辆的路径、节约时间、降低成本等方面具有十分突出的现实意义[4]。
车辆运输路径问题(VRP)是应急物流研究的基本问题,也是在有限时间内实现物资及时送达、提高救援效率、将灾害降到最小化的有效途径[5]。VRPTW问题是VRP问题的带时间窗约束的分支问题,接近现实场景中的任务需求,属于NP难题,其计算量会随着问题规模的增大而呈指数增长[6],传统的精确算法在此场景下难以在规定时间内求解,而启发式算法适用于计算大规模问题,所以成为了学者们研究的重点。关于此类问题的求解,学者们依次提出禁忌搜索算法[7-8]、蚁群算法[9-10]、遗传算法[11-12]、粒子群算法[13-14]等多个算法。本文采用的是李彤等[15]提出的PGSA算法,它最初被用于解决非线性整数规划问题,由于其算法原理不需过度依靠参数,性能优越,因而被学者广泛应用于许多工程技术领域。
曹庆奎等[16]设计了用以求解VRPTW问题的PGSA算法,结合车辆调度的物流任务需求,建立客户需求随机性机会约束模型,在求解效率上与传统的遗传算法进行比较,验证PGSA算法是一种有效的方法。石开荣等[17]在对PGSA算法基本原理进行深入研究之后,结合植物实际生长规律,提出双生点并行生长机制来增加了寻优搜索路径,拓宽搜索覆盖面,降低陷入局部最优解的概率。石开荣等[18]提出可生长点集合限定机制、可生长点剔除机制以及混合步长并行搜索机制,其核心思想是使用一种筛选优质可生长点的策略,有效控制计算规模、提高搜索能力。然而,优质点的筛选虽然可以提高解的搜索能力,但会导致解过早收敛,且一定程度上去除了劣点的搜索机会。
PGSA算法依赖于初始值,初始值的质量关系着算法的求解性能,且后期收敛性较差,容易陷入局部最优解。所以本文在文献[16]和文献[18]基础上对PGSA算法做了3个方面的改进:设计双阶段的PGSA搜索方案、增加有向生长机制和局部解跳出机制。首先,在算法的开始阶段,将问题简化为TSP问题进行处理求解,迭代一定次数之后得到第二阶段算法搜索的初始解,再使用本文改进后的生长策略,计算问题最优解。同时本文针对PGSA的过早收敛问题,引入局部解跳出机制,使其能在一定次数的搜索之后,跳出局部最优。最后,利用Solomon中的标准算例进行测试,与原始算法[16]进行对比。
1 背 景
1.1 VRPTW问题描述
VRPTW问题[19]一般被描述为:客户、配送中心的横纵坐标已知,给定每个客户配送需求,车辆从配送中心出发对每个客户进行配送,且只可访问客户一次,每辆车所配送需求量之和不可超过车辆最大载运量和行驶距离[20],此外,各个客户存在的时间窗要求也需考虑在内,车辆必须在时间窗[ei,li]内服务客户,以行驶距离最短为目标进行车辆调度,完成客户配送任务。
1.2 VRPTW数学模型
对于VRPTW问题,通过建立通用的数学模型来进行计算。设有N台配送车辆存在于配送中心,每台车辆(编号k)的载重量为Capk,行驶距离上限为Dk,现需配送M个客户,每个客户i的需求量为qi(i=1,2,3,…,M),每个客户要求的配送时间窗为[ei,li],配送中心的标号为0,客户i到客户j的距离为dij(i,j=0,1,2,3,…,M),tij表示配送车辆由客户i行驶到客户j的行驶时间,ti表示车辆到达顾客i位置的时间[21],tsi则表示车辆需要在客户i处的服务时间。再设nk为第k辆车配送的客户数(nk=0则表示未使用第k台车),集合Rk表示第k辆车行驶的路径,其中的单个元素rki表示客户rki在路径Rk中的顺序为i[22]。rk0=0代表车辆k是从配送中心0出发,初始时间t0赋值为0。
目标函数:
(1)
约束条件:
(2)
(3)
0≤nk≤M
(4)
(5)
Rk={rki|rki∈{1,2,…,M},i=1,2,…,nk}
(6)
Rk1∩Rk2=φ, ∀k1≠k2
(7)
(8)
ei≤ti≤li;i=1,2,…,M
(9)
(10)
其中,式(1)表示行驶距离最短的目标函数;式(2)与式(3)表示容量约束、距离约束,式(6)与式(7)表示客户只被一辆车服务一次,式(9)与式(10)代表时间窗约束和递推公式。
2 PGSA算法的优化设计
2.1 PGSA算法原理
PGSA算法(模拟植物生长算法)是将优化问题的解空间视作植物的生长环境,通过模拟植物生长的分支模式(L-系统),以植物的向性运动为启发式准则进行优化问题求解的近似算法[19]。
L-系统的形式化描述:破土而出的主干会在称之为节的地方长出新枝,新枝也会因为形态素的规则长出更新的枝,这种生长过程会反复进行,各个新枝彼此之间存在相似性,整个植物由自相似结构构成[23]。
PGSA算法在搜索空间中通过模拟植物生长的方式来搜索最优解,求解过程中得到的生长节点可以作为此类优化问题的可行解。生长节点的形态素浓度决定了该节点被选择作为新枝的可能性,形态素浓度更高的节点具有更高的环境适应性,更容易被选择。
设一棵树从树根所在点x0开始生长,形成树干X0,经过计算,选取形态素浓度超过x0的点作为生长点,假定这些点为X01,X02,…,X0k,每个点对应的形态素浓度为PX01,PX02,PX03,…, PX0k,其计算公式如下:
PX0i=[Z(x0)-Z(X0i)]/Δi,i=1,2,…,k
(11)
其中:
(12)
Z(X)表示生长点X的环境信息(目标函数值),也被称作背光函数,函数取值越小的生长点,对应生长点的阳光照射条件就越好。由以上2式不难看出,迭代计算中各点形态素浓度之和始终为1。目标函数值越小,该点的形态素浓度就越高,被选中的概率就越大。PX01,PX02,PX03,…, PX0k共同组成和为1的区间,随机生成一个[0,1]的实数,其在哪个生长点的区间内,就被选作生长新枝。如果实数生成在PX03的区间,那么生长点X03就会长出树枝X1,假设树枝X1上有q个生长点X11,X12,…,X1q,对应形态素浓度为PX11,PX12,…,PX1q。生长新枝以后植物的生长环境会发生变化,所以需重新计算形态素浓度,公式如下:
(13)
(14)
其中:
(15)
(16)
以此类推,反复进行此过程,直到迭代结束。
2.2 双阶段PGSA算法
文献[16]在对现有VRP问题研究的基础上,使用PGSA算法分开处理VRPTW的目标函数和约束条件,得到最终解决方案。但是原PGSA算法在求解过程中,结果收敛性差,容易陷入局部最优解,算法策略有待进一步改善。由于PGSA在搜索生长点时,对于初始值的依赖性较强[24],算法随机生成初始调度方案的方式,对求解精度影响较大。所以,本文针对初始值的质量问题,设计双阶段的PGSA算法,并且改进生长点的生长策略。在算法的初始阶段,原有VRPTW问题被理想化为一个不考虑需求,只将路程作为评价标准的TSP问题,针对此问题展开初始阶段的邻域搜索。
TSP问题又被称作旅行商问题,研究者通常将其视作VRP问题的一个特殊变体,被描述为一个旅行商从一个城市出发,经过所有城市后回到出发地,选择行进路线使得总体行程最短的问题[25]。
其评价公式为:
(17)
根据VRPTW问题和TSP问题的定义,不难看出它们实质上都是NP难题,在多项式时间内无法验证一个解的正确性。问题规模n的情况下解空间的大小为n!,随着n的增大,计算难度呈指数上升。
在这种情况下,传统精确算法无法在规定时间内求解问题,因此,针对这一点,国内外学者重点使用近似算法和启发式算法2类算法求解大规模问题。本文引用的PGSA算法是启发式算法的一种,它通过在搜索过程中获得的启发式信息来引导搜索,消除组合爆炸,使得问题的复杂度降低,同时降低了搜索工作量。
下面给出算法的可行性证明:
设在迭代搜索的过程中,针对每次迭代的生长点s∈S,S代表符合解的状态空间中的所有点集,s是其中一个元素变量(下文中的route即为s,代表每一代搜索的起始算子),由s的取值序列构成了迭代过程中的初始状态集合{s0,s1,s2,…,sn};每次迭代都可以视作对状态s进行一次搜索。而搜索操作的结果是生成了以s为起点的搜索集合以及产生了集合中的最小值s*。定义S上的Next-State关系为T,T⊆S×S,它可以产生各种行为,每个行为可以表示成s1→s2→s3…的形式,并且满足∀i,
1)Init⟹Inv
初始化时,s=s0显然成立。
2)Inv∧T⟹Inv
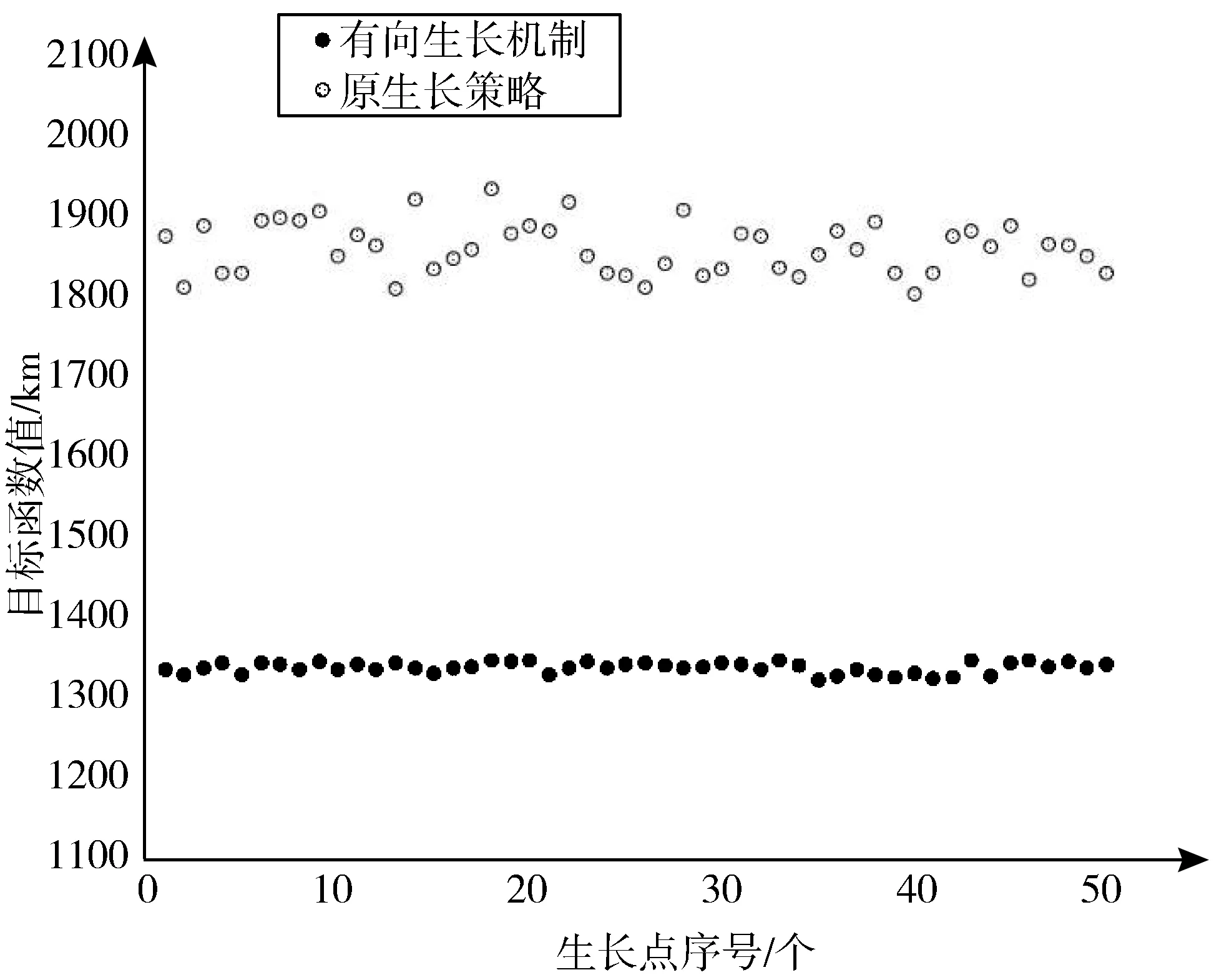
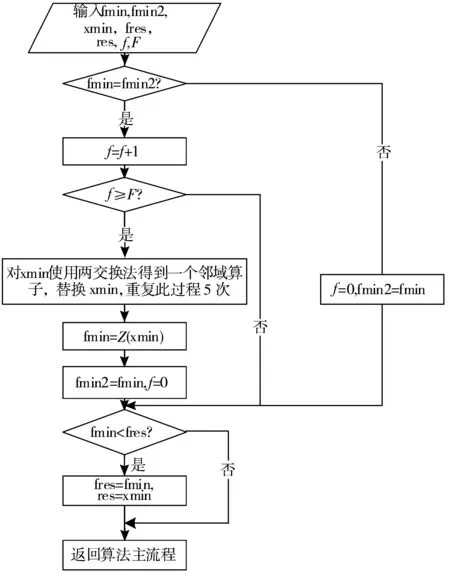
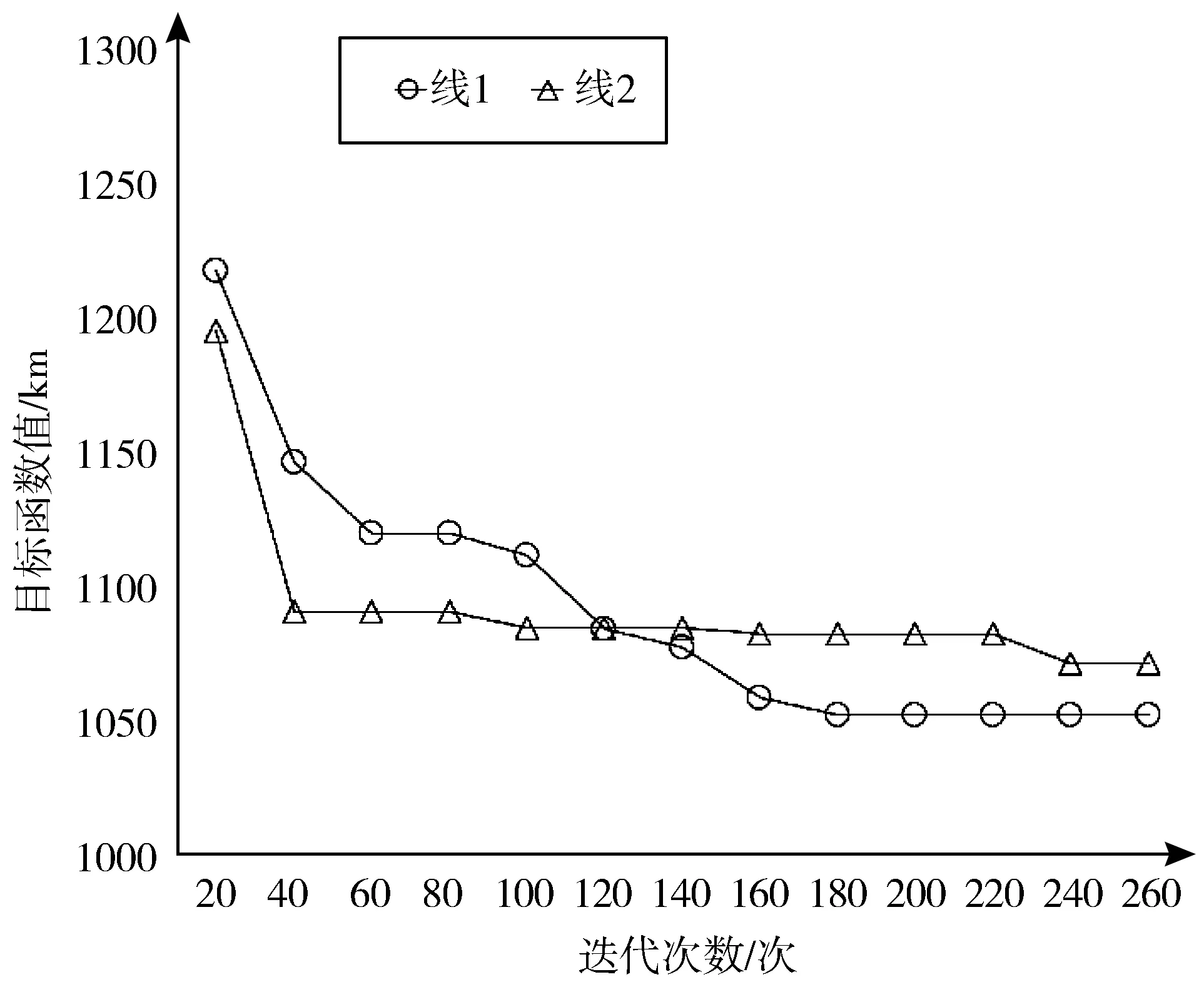
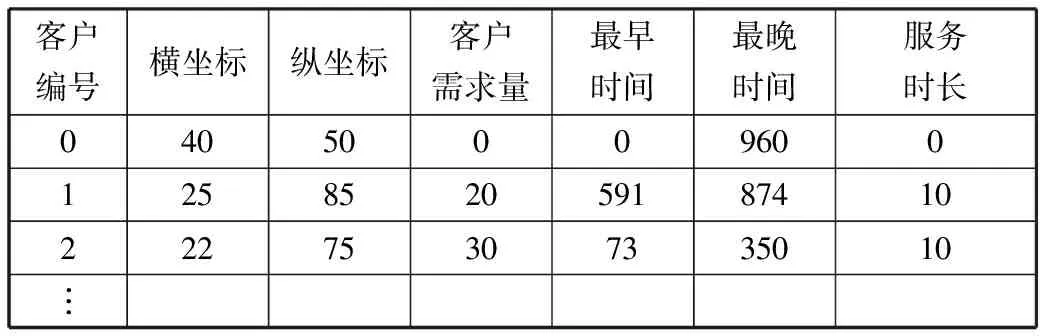
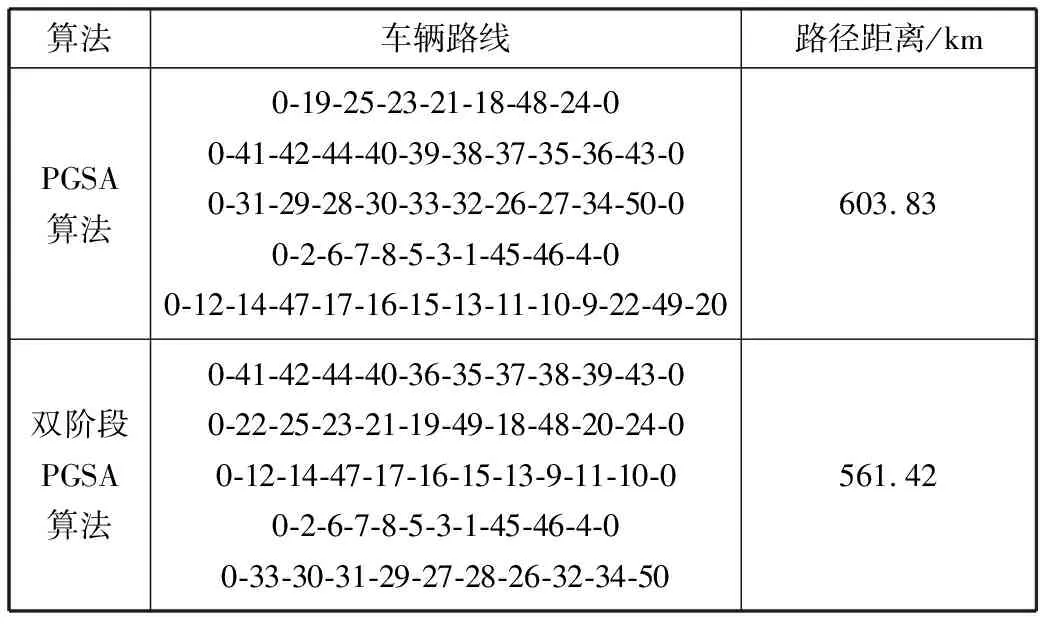
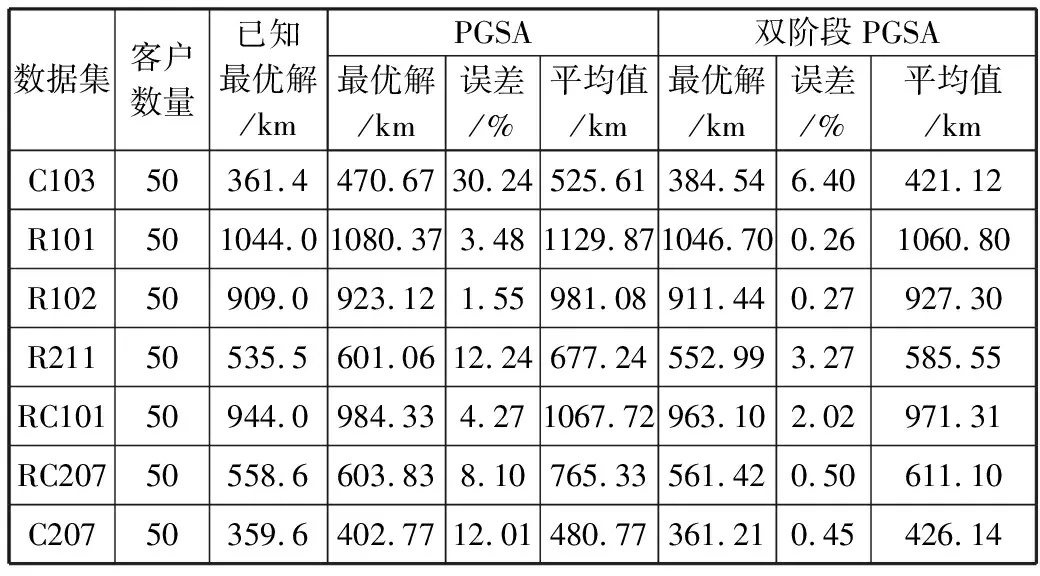
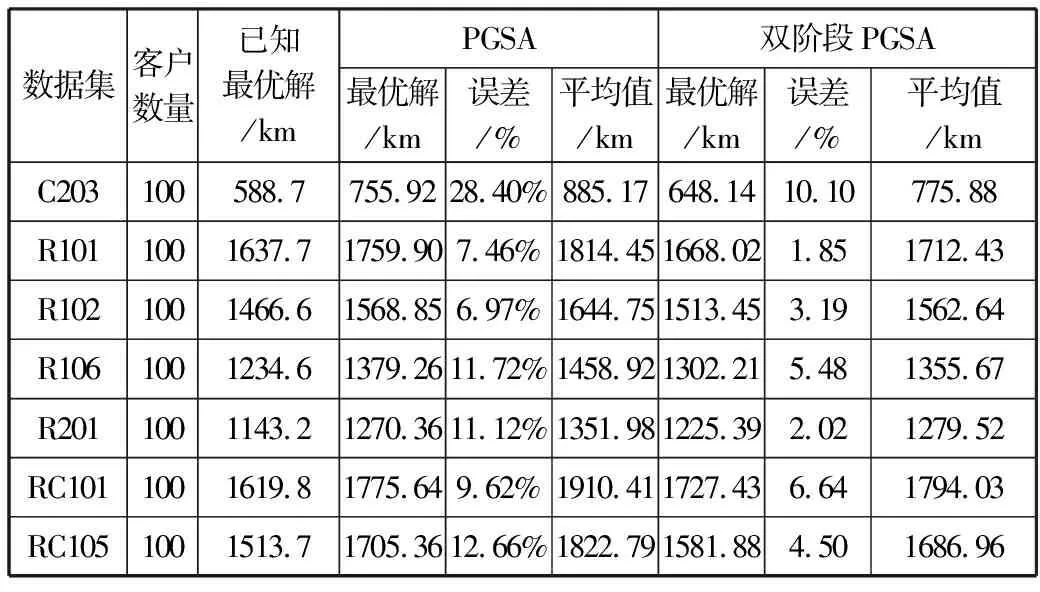
设当前状态满足Inv,那么Search(s)=Search(s0)=s*,设s的邻接状态为s′,s*不是不变式Search(s′)的搜索结果,即Search(s′)=h,∃h∈S,h 3)在程序执行结束时,s*=Search(s)=Search(s0)。 综上,在计算复杂度高的问题中,采用本文的启发式算法可以在迭代一定代数之后取得较优解。 改进后的PGSA算法基本流程见图1。 图1 基本流程图 2个阶段共用同一个算法基本流程,但在第一阶段开始时,初始算子route是随机生成,并且第一阶段的目标函数来自于公式(17)。而在第二阶段开始时,初始算子route使用的是第一阶段搜索得到的res,第二阶段的目标函数来自于公式(1),使用VRPTW的约束进行解的评估、搜索,在经过双阶段搜索之后,最终生成较高质量解。 本文在5个规模为50的数据集上分别使用单阶段PGSA算法与双阶段PGSA算法进行测试,记录20次实验所得最优值、平均值,并将其与已知最优解之间的误差计算值作为纵坐标,结果如图2和图3所示。从图中不难看出,双阶段的搜索方案误差更低,解的质量得到了有效提高。 图2 最优解误差对比图 图3 平均解误差对比图 在选定生长点route之后,PGSA算法会对route进行邻域搜索。但搜索过程中,较多劣质的生长点会保留在可生长点集合中,大大降低了其优化效率[18]。针对这一问题,本文提出一种有向生长机制,在每代进行搜索时,更改生长策略,优先将route点有向变换到当前最小值xmin,使route能够在生长开始时得到一个初始的生长方向,之后对route进行邻域搜索,选取搜索过程中得到的最优邻域算子更新xmin。具体的流程见图4。 图4 算法route的有向生长子流程 图4中xmin.size代表xmin算子的大小,xmin[i]代表算子中的第i个元素,可取范围为1~M。 如果在搜索过程中,搜索点通过插入法得到结果不优于当前生长点route,则会对route进行两交换法搜索。经过上述2个搜索过程之后,如果不能更新route,则会结束本次迭代中的搜索过程。 图5是数据规模为50的RC101算例在迭代次数为15次时候搜索得到生长点的样本图。随机选取2种策略下该代搜索所得的50个生长点样本,从图中可以看出,使用有向生长机制优化之后的PGSA算法搜索得到的生长点目标值更低,搜索效率更高。 图5 生长点样本图 在多次迭代搜索以后,PGSA可能会陷入局部最优解,为了跳出局部最优解,本文设计跳出机制。定义历史最优解fres、当前最优解fmin、频率判断最优解fmin2这3个变量。如果在搜索得到的最小值出现次数f(即当前最优解与频率判断最优解相等的次数)超过一定频率F之后,对其连续使用5次随机交换操作,得到新的算子,替代原来的最小值。同时将f置0,更新当前最优解、频率判断最优解、历史最优解,重新开始下代搜索。具体流程见图6。 图6 局部解跳出子流程 如图7所示,对R101算例进行测试,客户数量为50个。线1是使用局部解跳出机制的算法曲线,线2是未使用局部解跳出机制的算法曲线,纵坐标是该代搜索得到的历史最优解res目标函数值fres。从图中可以看出,引入局部解跳出机制之后,算法取得了更好的收敛结果。 图7 结果对比图 PGSA优化算法设计要点包括: 1)解的表示方法:客户直接排列法。 2)解的评价方法:采用式(1)对解进行评价。根据客户要求将货物按时送达的时间窗约束,将解中的元素依次纳入到各条配送路径中,在不满足时间窗约束时,结束本条配送路径,并将剩余点分配给下一车辆。最早计算出该解的评价值E。 3)邻域算子搜索方法:两交换法、插入法。 4)搜索规模:N2。 5)邻域算子的确定:从当前算子的邻域中选择搜索过程中评价值最高的邻域算子。 6)生长点选取策略:随机数法。 7)终止准则:采用迭代指定步数的终止准则。 邻域算子搜索方法包括: 1)插入法:使用随机函数,随机生成一个客户编号,并将其插入到算子的任意位置。 如原算子是0-5-6-2-4-3-1,任意选取一数字3,将其插入到客户6和客户2之间,得到邻域算子:0-5-6-3-2-4-1。 2)两交换法:使用随机函数,随机生成2个客户编号,交换其位置。 如将上述算子中的客户5、1位置交换之后,可得到邻域算子:0-1-6-3-2-4-5。 引入两交换法是为了使搜索过程中避开局部最优解,提高算法搜索效率。在对当前解进行搜索时,如果插入法搜索得到的邻域算子不优于当前算子route,则会再对当前算子route进行一次交换搜索。 本文采用VRPTW的Solomon算例集测试双阶段PGSA算法的求解性能。使用Win10系统、CPU i7-5500U、RAM 8 GB、Java语言编程实现,软件为VScode。表1是以RC207算例所展示的Solomon标准数据格式。 表1中,第1列代表客户编号,客户0代表仓库位置,第2列代表客户位置的横坐标,第3列代表客户位置的纵坐标,第4列代表客户所需物资数,第5列代表最早交付时间,第6列代表最晚交付时间,最后一列代表在该客户点服务时长。 表1 RC207数据,车辆数目25,容量1000 计算得到RC207算例的解决方案如表2所示,在车辆路线一栏,每行代表一个车辆的行驶路径,车辆从配送点0(仓库)出发最终返回配送点0(仓库)。 表2 RC207算例解决方案 本文实验部分采用的Solomon benchmark是一个用于研究VRPTW问题的标准数据算例集。其中R1和R2的客户位置是随机生成,而C1、C2的客户位置则较为集中,RC1和RC2则混合了随机分布以及集中分布的客户位置。此外,R1、C1、RC1的任务时间窗排列较为紧凑,R2、C2、RC2的任务时间窗排列则较为宽松。实验考虑实际配送工作中客户位置、数量和时间窗口分布不同的情况,针对不同规模(分别包含25、50、100个客户)、多种客户分布类型的Solomon算例,使用原PGSA算法和改进后的双阶段PGSA算法计算20次,并记录下每次的运行结果,计算平均解、与数据集所提供的历史最优解的误差,结果记录到表3~表5中。 表3 PGSA与双阶段PGSA在25个客户规模数据仿真对比 表4 PGSA与双阶段PGSA在50个客户规模数据仿真对比 表5 PGSA与双阶段PGSA在100个客户规模数据仿真对比 为了进一步验证双阶段PGSA算法的性能,采用蚁群算法(ACO)、禁忌搜索算法(TS)、自适应大邻域搜索算法(ALNS),对Solomon数据集中100个客户规模的算例进行求解,6种类型算例各选其一进行对比实验,结果记录在表6中。 表6 双阶段PGSA于ACO、TS、ALNS仿真对比结果 单位:km 实验选取21个算例对改进后的算法和原算法进行测试,通过结果比对,双阶段PGSA在最优解的求解问题上表现出了较好的收敛性,并且也提高了平均解的质量。原始PGSA算法在小规模数据集上的求解质量较好,但随着数据集计算规模的增大,原始PGSA算法对最优解的求解能力逐渐下降,本文改进后的有向生长机制和局部解跳出机制可以提升PGSA算法在大规模数据集上的搜索能力,提高搜索效率,有效改善算法过早陷入局部最优解的情况。 从表6与其它算法的对比结果看,本文改进之后的双阶段PGSA算法在6种不同类型的算例中都取得了一个较优结果,除去在C105算例实验中高于TS算法,在C203、RC203算例实验中高于ALNS算法之外,其它算例中都取得了不错的收敛结果。 在分析PGSA算法的基础上,本文的双阶段策略通过对初始解构造的优化,提高了解的搜索质量,使算法搜索效率提升。这个策略的优点是易于实现,代码复用率高。有向生长机制的引入可以使得迭代开始时所选取的生长点可以有导向地收敛到当前局部最小值,提高当前邻域搜索的效率。局部解跳出机制可以在算法陷入局部最优解时,破坏解的结构,从而搜索到更好的解决方案。 PGSA算法的生长策略与生长点选取策略对求解效率起着重要作用。本文的有向生长机制与局部解跳出机制都仅是对生长策略的优化,这2个机制的设计方式是否会对求解性能产生影响,还需继续深入研究。而对于PGSA算法本身来说,在其计算大规模算例的过程中暴露出内存占用高的缺点。如何针对这一缺点,优化生长策略和生长点选取策略,对PGSA算法求解效率的提高会有很大帮助。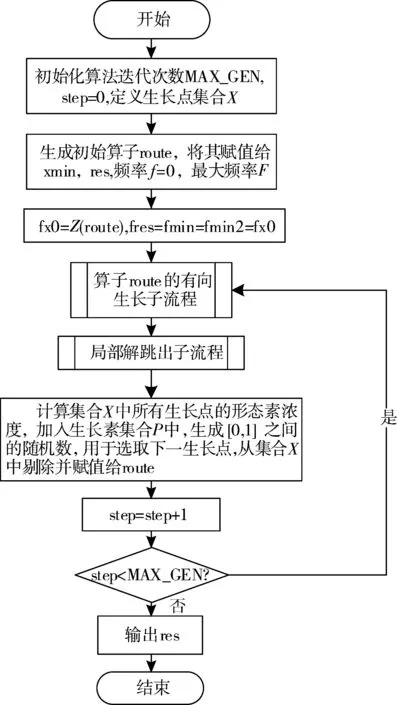
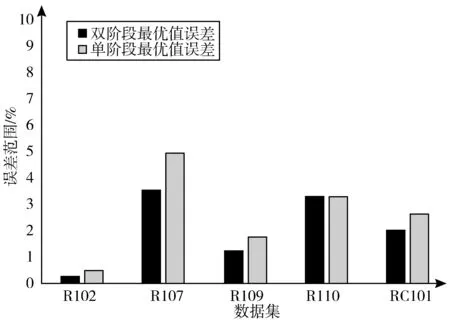
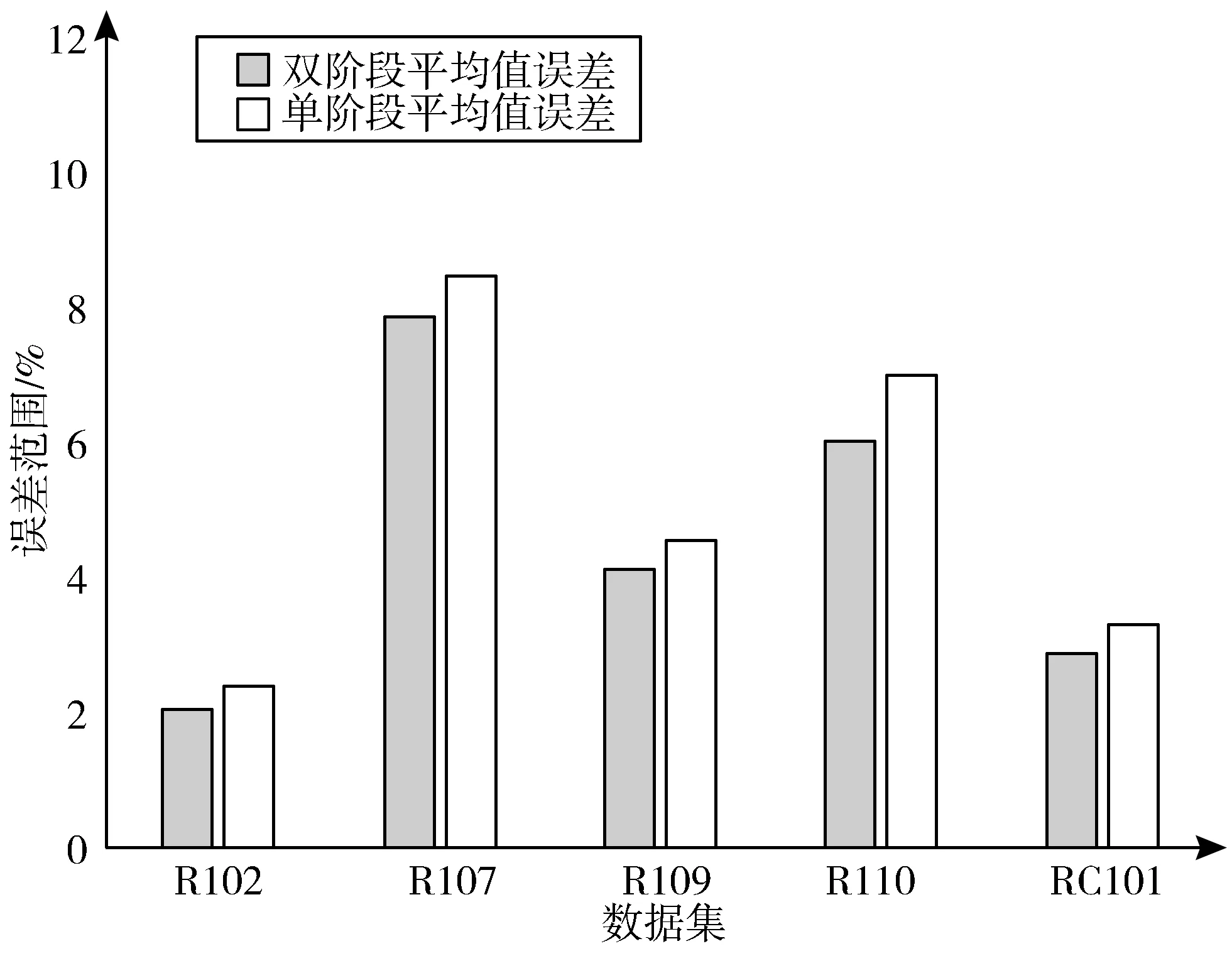
2.3 有向生长机制
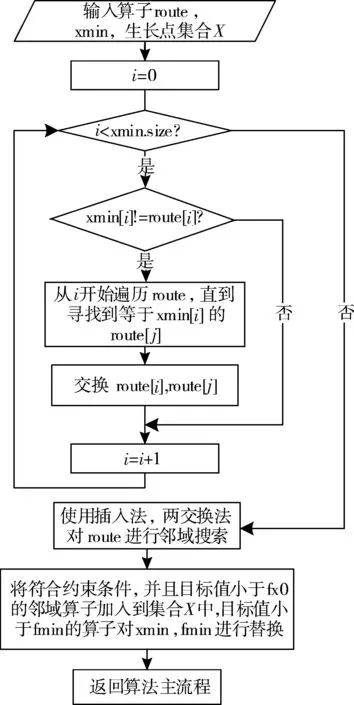
2.4 局部解跳出机制
2.5 PGSA优化算法设计要点
3 实验分析


4 结束语

