板肋加劲板整体稳定数值模拟与受力机理研究

赵 秋，陈 鹏，林志平，张骏超

(1. 福州大学土木工程学院，福建福州 350108； 2. 福建省高速技术咨询有限公司，福建福州 350001；3. 福建省高速公路工程重点实验室，福建厦门 361001； 4. 福州市规划设计研究院集团有限公司，福建福州 350108)

0 引 言

板肋加劲板以其构造简单、施工方便等优点而常常用于钢箱梁的腹板、组合梁桥的钢板梁腹板以及钢塔、钢墩、钢箱拱中。当受压加劲板的加劲肋刚度比小于临界刚度比时，轴向压力的增大将会引起板肋加劲板的整体失稳变形[1]。早期国内外学者对于稳定的研究多是基于弹性力学的理论推导。随着计算机发展，数值模拟分析成为了主要科研手段，国内外学者采用有限元数值模拟与相关试验相结合的方法获得了较为理想的结果[2]。方淑君等[3]通过对钢箱梁受压翼缘的局部稳定试验，验证了有限元计算模型的正确性，并提出对应的稳定临界应力理论。赵秋等[4]通过对闭口肋、开口肋加劲板的试验验证了有限元模型的正确性。可见，对于加劲板的有限元模型已经得到了较好的验证。

在此基础上，多位学者采用基于试验验证的有限元模型，对开口肋加劲板的受压力学性能进行分析，发现初始几何缺陷对于开口肋加劲板受力性能的影响较为显著[5]。翁雅谷等[6]建立了高强度钢开口肋加劲板的三维实体弹塑性模型，并经轴压试验验证该模型的正确性后，分析了几何缺陷对承载力的影响，发现几何缺陷为影响板件承载性能的主要因素。王欣南等[7]以某座钢箱梁截面中的板肋加劲板为有限元分析的对象，在考虑了整体几何缺陷与残余应力的条件下得到了该加劲板的极限承载力。Sadamoto等[8]通过算例数值模拟和有限元验证相结合的方法，研究不同几何缺陷条件下板条加劲肋的受力行为，并基于破坏时发生的不同屈曲行为提出相应的板壳分析方法。此外，赵秋等[9-10]建立经验证的加劲板焊接过程的三维热弹塑性有限元模型，得到了加劲板焊接残余应力分布，提出了残余应力分布的简化计算方法。

中国现行钢桥规范关于加劲板稳定的条文来自于国外规范，目前仍然有必要针对受压加劲板稳定进行系统研究，形成适用于中国的钢桥加劲板稳定设计体系。本文采用经由试验验证的同时考虑焊接残余应力和几何缺陷的受压加劲板数值模拟方法，对板肋加劲板受压整体稳定受力机理进行分析，明确初始几何缺陷对于加劲板整体失稳的影响，研究板件由于不同侧缺陷而引起整体失稳的破坏机理，为板肋加劲板的设计方法研究提供参考。

1 有限元数值模拟方法

1.1 有限元模型

采用ANSYS有限元软件对验证试件进行模拟。由于梁单元可以较好地模拟长柱整体稳定受力[11]，且长细比较大的整体稳定(中长)长柱验证试件受压时最可能发生板肋与被加劲板共同弯曲变形的整体失稳现象，因此采用铁木辛柯梁Beam188单元(3D线性有限应变梁单元)。考虑到整体稳定短柱验证试件还出现了板件的局部变形，而Beam188单元无法模拟这种情况，故补充可考虑板件局部变形的Shell181单元(有限应变壳单元)进行对比分析。因此，后文将分别用上述两种单元进行对比验证，两种单元的有限元模型见图1。此外，有限元模型均采用两端简支的边界条件，在转动中心处分别设置一个Mass21质量单元主节点，并将模型上、下端面全部节点与其耦合，约束截面绕强轴与弱轴的转动自由度,同时考虑焊接残余应力以及初始几何缺陷的影响。

1.1.1 初始几何缺陷

在进行非线性屈曲分析时，需要在有限元模型中引入初始几何缺陷以激活非线性效应。本次模拟中考虑半个正弦波的初弯曲，通过激光水准仪构造水平面，结合数显游标卡尺量测各验证试件中部的初弯曲幅值，结果见表1。对于Beam188梁单元，通过在建模时直接考虑节点的坐标位置来计入分布形状为半个正弦波初弯曲的影响；对于Shell181单元，将试件的第一阶屈曲模态变形，按照模态变形中最大节点位移与实测缺陷幅值相同的原则，利用UPGEOM命令对整个模型的节点位置进行更新。

表1 试件中部初弯曲幅值Table 1 Initial Bending Amplitude in Middle of Specimen

1.1.2 焊接残余应力

有限元模型中考虑加劲肋与被加劲板焊接所产生的焊接残余应力。残余应力采用文献[12]中提出的简化分布，如图2所示，其中hf为焊脚尺寸，ts为板肋厚度，b1～b3、h1～h3分别为被加劲板与板肋的残余应力分布范围，bm为母板宽度，hs为板肋高度，ft、fc与ftb、fcb分别为被加劲板与板肋的残余拉、压应力，其值可按文献[12]中的式(1)简化计算。两种单元在考虑了残余应力后的轴向应力分布见图3。

对于Beam188梁单元，通过梁截面积分点坐标编写初应力文件，然后在/SOLU中采用INISTATE命令读入该文件以考虑残余应力；对于Shell181单元，直接在/SOLU处理器中由单元的形心坐标通过INISTATE命令直接定义残余应力值。

(1)

式中：tm为母板厚度；fyj为被加劲板屈服强度；fyb为板肋屈服强度；fy为试件屈服强度。

1.2 本构关系

采用验证试验中同批次钢板进行材性试验，其中Q345钢材屈服强度为378 MPa，抗拉强度为450 MPa，弹性模量E=2.05×105MPa。验证试件的有限元模型均采用Von Mises屈服准则，本构关系选用最贴切实际钢材拉伸应力-应变曲线的三折线本构。Q345钢材采用的本构关系如图4所示。

2 有限元模型模拟方法验证

2.1 整体稳定试验

整体稳定试件设计采用单一变量法，仅变化试件长度以探究其整体稳定性能。选取其中6个Q345钢材组的板肋加劲板整体稳定试件的试验结果，建立对应的有限元模型，进行模型准确性与可靠性验证。6根验证试件的实测尺寸见表2，横截面尺寸见图5。为方便描述，后文将长细比85.8和109.5的试件称为长柱试件；长细比44.4的试件称为中长柱试件；长细比17.8的试件称为短柱试件。

表2 板肋加劲板整体稳定试件实测尺寸Table 2 Measured Dimension of Overall Stability Specimen of Stiffened Plate with Plate Rib

为实现试验试件两端的简支边界，试件底部采用压力机自带的球铰以实现转动；顶部设计了能绕试件弱轴转动的单向铰，该铰从上到下分别由上部固定板、半圆柱滚轴以及转动板组成，见图6。加载时，在试件的两端都设置端板，对于长度较小的试件，其受压失稳时的临界应力较大，因此可能发生端部破坏先于整体失稳的情况[13]。出于试验加载的安全性考虑，将试件与端板以点焊的形式进行连接，尽可能降低试件端部焊接导致的强度削弱，见图7。加载初期采用荷载控制的加载方式，每级加载值约为有限元预估极限荷载的5%。当荷载达到有限元预估极限荷载的70%时改为位移控制加载，逐步达到荷载极限。

2.2 试件破坏模式验证

通过对比试验破坏模式与有限元破坏模式的吻合情况，判断有限元模型是否正确。图8～10为6个板肋加劲板整体稳定试件在极限荷载状态下的破坏模式与采用Shell181壳单元、Beam188梁单元模拟的有限元变形图和Mises应力图的对比。

由图8和图9可知，对于整体稳定长(中长)柱试件，试验试件与采用Shell181壳单元和Beam188梁单元建立的模型均发生了明显的弯曲失稳破坏。其中，试件Q3-HZ2、Q3-HZ4-1和Q3-HZ4-2均在试件中部发生了朝向板肋侧的明显弯曲；试件Q3-HZ3和Q3-HZ4-3则在试件中部发生了朝向被加劲板侧的弯曲变形。从对应的Mises应力图中可以看出，对于长柱试件，仅有板肋侧超过了屈服强度，但最大应力均并未达到抗拉强度；对于中长柱试件，除了板肋侧外，被加劲板也有部分超过了屈服强度，但试件的最大应力同样并未达到抗拉强度。

从图10可以看出，对于整体稳定短柱试件Q3-HZ1，试验试件与采用Shell181壳单元建立的模型均发生了朝向板肋侧的弯曲变形，同时肋间被加劲板以及板肋处出现了一定程度的面外变形，从Shell181单元模拟的试件来看，其中部板肋处Mises等效应力较高，且几乎接近于抗拉强度，体现出了一定的强度破坏特征。Beam188单元无法模拟各组成板件的局部面外变形，因此Beam188单元模拟的试件仍为试件的整体变形，进而导致模拟破坏形态与试验试件的差异较大。

2.3 试件承载力与应力-位移曲线验证

验证试件的实测极限轴向平均应力与有限元分析计算所得值的对比见表3。

从表3可知，Shell181单元计算结果与试验值的最大相对误差为4.2%，平均相对误差为1.48%，Beam188单元计算结果与试验值的最大相对误差为5.4%，平均相对误差为1.92%，误差均较小。

表3 验证试件极限荷载试验值与有限元数值对比Table 3 Comparison Between Test and Finite Element Value of Ultimate Load of Verification Specimen

将试验测得的整体稳定各类试件的轴向平均应力-轴向位移曲线与采用两种单元模拟所得的曲线进行对比，见图11～13。

从图11～13可知，采用两种单元的有限元计算结果与试验实测的轴向平均应力-轴向位移曲线均表现为前期直线上升、中期刚度退化、后期下降的三大阶段。从图11和图12可以看出：在前期直线上升阶段中，两者的轴向平均应力-轴向位移曲线基本重合，吻合度较好，这说明了材性试验所得的钢材各属性的准确性；在中期刚度退化阶段中，长(中长)柱生朝向板肋侧的弯曲变形，“2”表示试件中部发生朝向被加劲板侧的弯曲变形，“3”表示被加劲板与板肋板件发生局部变形。

试件的吻合度较好，其中采用Shell181单元模拟的Q3-HZ4-2试件的荷载-位移曲线与试验曲线基本重合[图11(c)]，这说明了试验设置的两端简支边界条件与理想的边界条件较为吻合。在后期下降阶段，长(中长)柱试件及两种单元模拟的试件都体现出达到峰值荷载后的突然下降，且下降幅度较大，具有一定的失稳特征。相比于长(中长)柱试件，从图13可以看出，整体稳定短柱试件在达到峰值荷载后仍有着较好的延性，但Beam188单元模拟的试件由于单元自身无法模拟板件的局部屈曲变形而导致最终曲线的走势与实际试件的出入较大。

综合以上分析可知，使用两种单元计算得到的误差均较小，采用Shell181单元可以较好地模拟受压板肋加劲板试件整体稳定性能，但在误差容许情况下也可以采用Beam188单元简化计算。

3 板肋加劲板受压整体稳定受力机理

3.1 试件概况

基于上文已验证的板肋加劲板整体稳定数值模拟模型，为更贴合实际工程运用尺寸，本节增设一组板肋加劲板作为分析对象，截面见图14，具体尺寸见表4，并采用偏差更小且能同时考虑板肋局部屈曲与加劲板整体失稳的Shell181单元进行模拟分析。模型的边界条件为两端简支。

表4板肋加劲板整体失稳模式构件几何尺寸Table 4 Geometric Dimension of Overall Instability Member for Stiffened Panel with Plate Rib

由第2.3节轴向平均应力-轴向位移曲线可知，三折线材料本构关系可以较好地反映板肋加劲板整体稳定构件的受力行为。因此，有限元模型本构关系以最贴合实际的三折线本构关系为准，其中各参数取中国《公路钢结构桥梁设计规范》[14]中的标准值，钢材屈服强度fy取为345 MPa，抗拉强度ft取为470 MPa，弹性模量E取为2.06×105MPa，流幅取0.18%。此外，有限元模型同时计入初弯曲与焊接残余应力的影响。其中初弯曲考虑构件发生半个正弦波的弯曲形式，并取初弯曲幅值为构件设计长度的1/1 000，即取4 mm；焊接残余应力以图2的简化焊接残余应力分布为准。

3.2 受力机理分析

从第2.2节试件的破坏模式可知，板肋加劲板可能发生不同朝向的整体弯曲失稳破坏，且两方向弯曲失稳破坏的荷载-位移曲线形式也有所差异。因此本节将分别对两种弯曲方向(朝向板肋侧或被加劲板侧，通过添加两种初弯曲方向实现)板肋加劲板的整体稳定破坏全过程进行分析。考虑到构件的最终破坏均表现为中部截面的面外变形过大，故以构件中部截面为研究对象，结合构件的轴向荷载-位移曲线，分析其在整个失稳全过程中的应力变化，借以说明两端简支加劲板的受力稳定机理。

两类构件的轴向平均应力-轴向位移曲线如图15所示。从图15(a)可知，往板肋侧弯曲的构件在荷载作用下构件中部面外变形逐渐增大，构件将从轴压状态变为压弯状态。根据截面形心弱轴的位置，中部截面的板肋侧与被加劲板侧将分别处于轴压应力与弯曲压应力、弯曲拉应力叠加的情况(二阶效应)。此外，随着面外变形的增大，由于板肋边缘距离截面形心轴位置更远，因此板肋边缘处的弯曲拉应力显著高于被加劲板边缘处的弯曲压应力，并进一步增大二阶效应[图16(a)，其中d1、d2分别为极限荷载时刻与最终破坏时刻板肋边缘与荷载作用轴的距离]。因此，原本受压的板肋边缘(应力为-116.5 MPa)逐渐变为受拉状态(应力为346.4 MPa)。继续增加荷载，当被加劲板边缘在轴压应力与弯曲压应力叠加作用下进入材料的强化阶段时，构件整体达到极限荷载[图15(a)中的点B]，此时板肋边缘处也有部分达到强化阶段，说明二阶效应产生的弯曲拉应力已经远远高于焊接残余压应力与轴压应力。而后曲线就进入了后期的下降段，板肋边缘主要受到弯曲拉应力作用，故板肋的受拉强化区域不断从板肋边缘往被加劲板侧发展[图15(a)中的点C]。

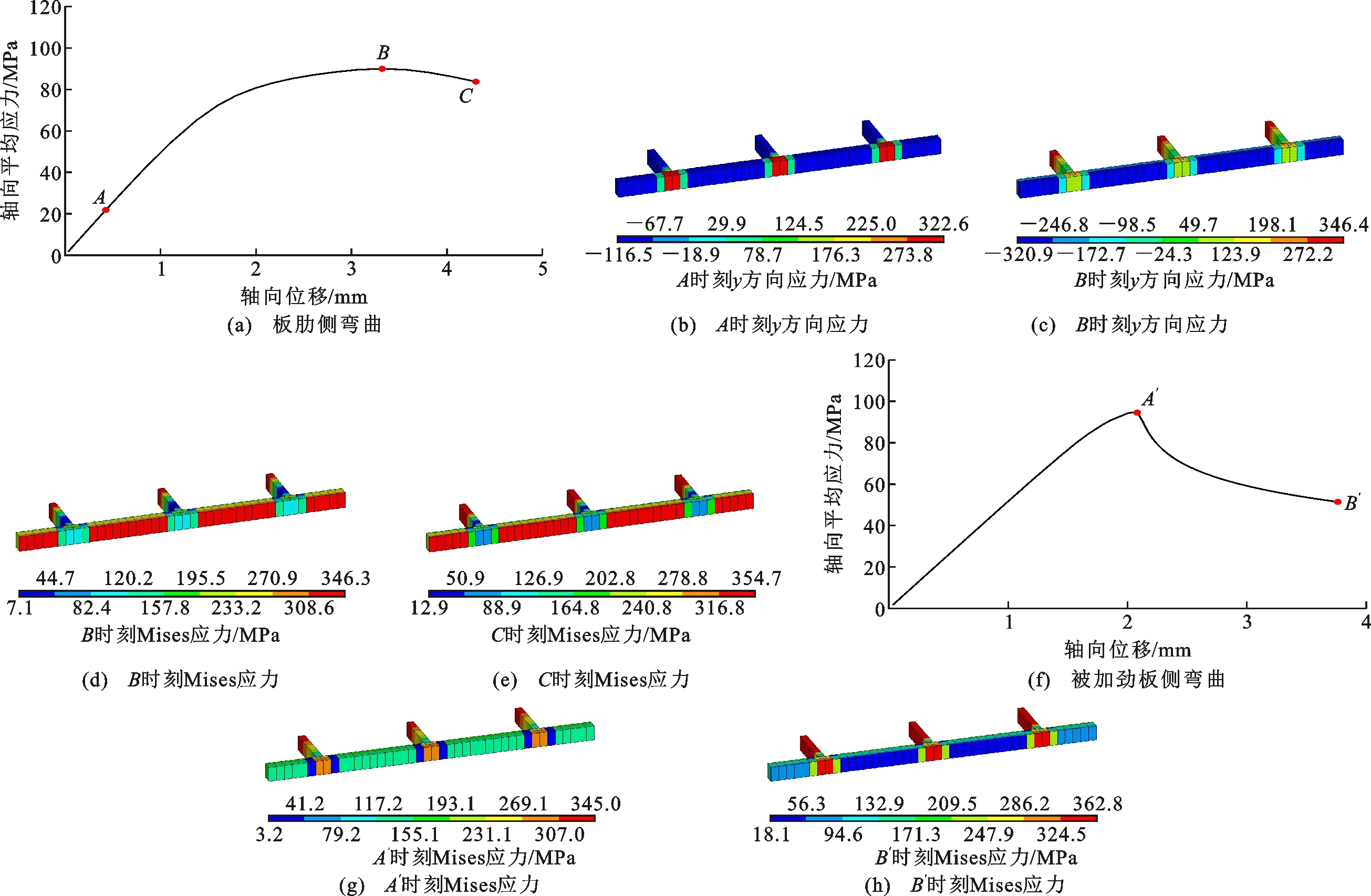
从图15(f)可知，往被加劲板侧弯曲的构件一开始的受力情况与往板肋侧弯曲的基本一致，不同的是，构件中部截面的板肋侧将处于轴压应力与弯曲压应力叠加的情况，被加劲板侧处于轴压应力与弯曲拉应力叠加的情况(二阶效应)。随着构件中部往被加劲板侧面外变形的增大，板肋边缘将不断靠近加载中心线，因此二阶效应并没有那么明显[图16(b)]。继续增加荷载，当板肋边缘在轴压应力与弯曲压应力叠加作用下达到材料的屈服强度345 MPa时，构件整体达到极限荷载[图15(f)中的点A′]，此时板肋的刚度下降，截面的形心轴不断往被加劲板侧移动，但被加劲板并未达到屈服。而后曲线进入下降段，构件面外变形快速增大，板肋的受压强化区域不断从板肋边缘往被加劲板侧发展，同时被加劲板仅在焊接残余拉应力区域达到了材料的强化阶段。

此外，对比图15(a)与图15(f)可知，不同弯曲方向构件的轴向应力-位移曲线在下降段幅度明显不同，其中被加劲板侧弯曲构件的曲线更为陡峭。这与截面的刚度相关：对于板肋侧弯曲构件，被加劲板与板肋边缘在极限荷载下均已达到材料屈服强度，随后强化区域往被加劲板处发展；对于被加劲板侧弯曲构件，仅有板肋边缘处受压达到屈服，强化区域往被加劲板处发展，但仅有残余拉应力分布处达到屈服强度。由钢材的本构关系可知，朝被加劲板侧弯曲构件的中部截面超过屈服强度的部分较少，因此整体刚度较大，则下降段更为陡峭。

两构件的轴向位移-轴向平均应力曲线对比如图17所示。可以看出，两曲线在前期直线上升段由于二阶效应并不明显而基本重合，随着荷载的增加，板肋侧弯曲的构件更早出现了刚度退化，且轴向平均应力的最大值也相对较低。由于实际构件的整体几何缺陷(初弯曲)方向具有不确定性，且往板肋侧弯曲的构件极限轴向平均应力较小。因此，对于实际工程中组成钢箱梁顶板的板肋加劲板，应特别注意在车轮作用下可能出现的朝向板肋侧的变形，在制作时应尽量避免朝向板肋侧的初始弯曲。

4 结语

(1)采用试件材性试验数据拟合的三折线本构模型，并考虑残余应力与初始几何缺陷的影响，结果表明：采用Beam188梁单元可以较好地模拟整体稳定长(中长)柱的破坏形态与荷载-位移曲线，但对短柱试件的吻合程度较低，梁单元模型与长(中长)柱试验试件的承载力最大相对误差为5.4%，平均相对误差为1.92%，与短柱试件的承载力相对误差仅为0.7%。采用Shell181单元模拟的整体稳定试件的破坏形态效果更好，与试验试件的承载力最大相对误差为4.2%，平均相对误差为1.48%。

(2)不同弯曲方向构件的轴向应力-位移曲线在下降段幅度明显不同，其中被加劲板侧弯曲构件的曲线更为陡峭。在极限荷载下：对于板肋侧弯曲构件，被加劲板与板肋边缘均已达到材料屈服强度，随后强化区域往被加劲板处发展；对于被加劲板侧弯曲构件，超过屈服强度的部分较少，仅有板肋边缘处受压达到屈服，强化区域往被加劲板处发展，但仅有残余拉应力分布处达到屈服强度。

(3)相比于被加劲板侧弯曲，板肋侧弯曲的构件更早出现了刚度退化，且轴向平均应力的最大值也相对较低。对于实际工程中组成钢箱梁顶板的板肋加劲板，注意在车轮作用下或者制作时应尽量避免朝向板肋侧的变形。