一种考虑反向缝的全球低轨卫星通信系统的波束排布方法*
李维梅,施锦文,崔 镇,崔兆云,周兰兰
(西安空间无线电技术研究所,西安 710100)
0 引 言
近年来,低轨卫星因其发射成本低、距离地面近、传输时延短、路径损耗小、数据传输率高等优点得到了迅速发展,卫星通信与互联网相结合组成的卫星互联网成为研究热点[1-3]。低轨通信小卫星技术应用灵活,其有效载荷的批量化、低成本研制是其主要发展方向。天线作为卫星有效载荷的眼睛,是低轨卫星发展的关键技术之一。天线技术在向着宽带、多频段共用趋势发展的同时,向着高集成度、低剖面趋势发展,并且需要兼顾低成本。对于全球低轨卫星星座方案的设计,还得考虑天线波束排布规划和实现能力[3]。
低轨卫星始终处于高速运动状态中,其典型特征就是动态性。由于相对运动,在首尾轨道之间会产生反向缝。以往对于卫星多波束技术的研究一般都是基于卫星波束或者是基于天线自身波束特性考虑波束之间的影响[4-6],不会涉及到反向缝问题。本文基于多种形式的卫星波束排布分析,考虑到反向缝区域的波束覆盖问题,其子波束采用长椭圆波束形式的矩形卫星覆盖形式,克服了采用其他波束形式时对波束资源的浪费,多个卫星采用相同的天线配置,批量化生产可以降低成本。通过分析载干比(C/I)结果得出这种波束排布能满足卫星通信的要求。
1 辐射场到地球覆盖区的转换方法
对于低轨卫星,要实现较大范围乃至全球的覆盖能力,通常需要由多颗卫星按照一定的形状和规则构建卫星星座系统。若采用多波束覆盖,每个卫星在地面的覆盖区是其配置天线的多个波束的组合,当轨道高度和轨道倾角等卫星参数一定时,卫星配置天线的波束照射能力决定了单个卫星的覆盖能力,覆盖全球需要的卫星个数可以认为是由天线的波束能力确定的,通过天线在地面的照射覆盖分析就可以确定卫星的服务区。
1.1 坐标系定义
如图1(a)所示,u和v分别定义为
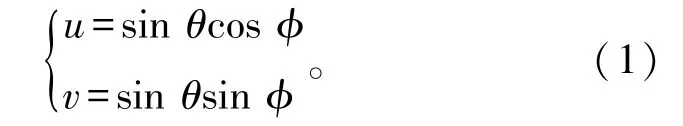

图1 坐标系转换关系图解
从公式(1)可以看出u和v分别为球坐标系单位矢量在XY平面上的投影,因此UV在XY平面上投影为矩形。UV坐标系单位矢量为

且有u2+v2≤1。
建立卫星与地球坐标系,如图示1(b)所示。卫星坐标系的X轴平行于赤道面指向东,Z轴指向星下点,Y轴根据X、Z轴定义满足右手螺旋定律指向南。地球坐标系的坐标系原点为地球地心,其X轴由地心指向卫星,Z轴由地心指向北极,Y轴满足右手螺旋定律指向东。在图1(b)地球坐标系下,对于地球上的任意一点A,OA″表示OA在地球XOY平面上的投影,A'表示A点在Z轴上的投影。由图1(b)可以看出,∠AOA″表示地球的纬度,∠XeOA″表示地球的经度。
1.2 UV坐标系下的辐射场到地球经纬度的转换
如图1(c)所示,地球坐标系的+X轴由地心指向卫星,假设星下点经度为lonsat,卫星位于S点,A为地球上的某一点。其中,卫星轨道半径OOS为Ro,地球半径OA为Re。假设A点在卫星坐标系OS点处的U、V坐标已知,求得A点在地球坐标系中的坐标(xA,yA,zA),再根据xA、yA和zA可以求得A点经纬度信息,便可以实现UV坐标系到地球经纬度的转化。
根据A点的U、V坐标值求得θ和φ的值分别为

式中:θ和φ的定义如图1(a)和图1(b)中的卫星坐标系所示。
图1(c)中,θ为卫星点OS与A点的连线和OS与地心O的连线的夹角;OSA方向对应图1中^r矢量方向;OSO所在方向对应图1中ZS方向;C点表示OS与A点的连线的延长线与YOZ面的交点;∠OSOC=90°。经过O点做OSC的垂线与OSC相交于D点,根据几何关系,可得∠DOC=θ。由图1(c)可知,OD的长度h为

图1(c)中,OA在XZ面上的投影为OB,OB的长度为xA。∠AOD=θ',∠AOB=θ″,根据图1(c)中的几何关系,即
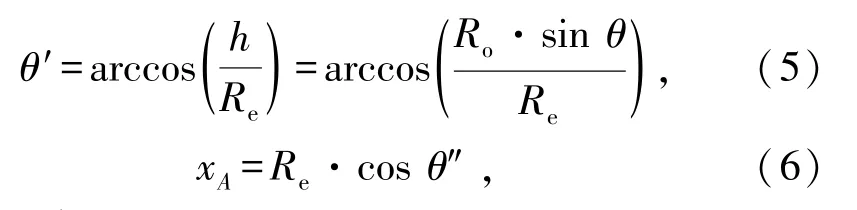
进而可以求得

A点与X轴的距离ρ为

图1(c)中,φ为OC与Y轴的夹角,也即YOZ平面与OSOC平面的夹角为φ。由前面的推导已知∠OSOC=∠OSBA=90°,因此φ为OA在YOZ面上投影与Y轴的夹角,于是可得

根据A点的X、Y和Z坐标xA、yA和zA,可以得到A点的经纬度分别为
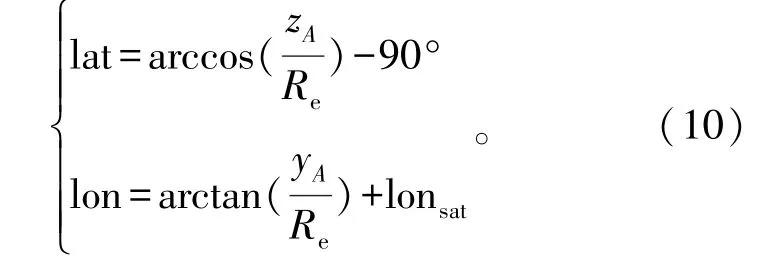
在公式(10)中,纬度减掉90°的目的是保证北纬为正、南纬为负;经度加上星下点经度是因为默认地球坐标系中+X轴方向为东经0°。
UV坐标系下的天线辐射场输出是很多组(u,v)网格下的场值,即每一个天线辐射场值的位置由每一组(u,v)决定,将每一组(u,v)坐标值转换到经纬度坐标系下,便得到每一个辐射场在地球经纬度坐标下的位置,从而可以将UV坐标系下的辐射场在地球经纬度下绘制出来。
2 不同形状的卫星服务区覆盖分析
通过以上天线辐射场到地球覆盖区的转换方法的指导,对不同形状的卫星服务区形式进行分析。对于一种均匀配置的低轨道星座,其特点是每颗星与周围若干颗相邻卫星相连(可以是同轨道卫星,也可以是异轨道卫星)。根据第1节的坐标系转换分析,每个卫星对地面的覆盖可以看作是一个大的波束照射地面。采用OneWeb的一种卫星配置方案,轨道高度为1 200 km,轨道倾角为87.9°,总共有18个轨道面,每个轨道上有40个卫星。将UV坐标系下一定波束宽度的波束转化到经纬度坐标下,便可以绘制多颗卫星对于地面的通信服务区。要实现全球的无缝覆盖,当每个星的半张角取为28.9°时,可以实现图2(a)所示的全球覆盖。这里的波束也可以不采用具体的天线波束辐射场,采用数值方式绘制需要的覆盖形状就可以模拟多个卫星对地面的覆盖。
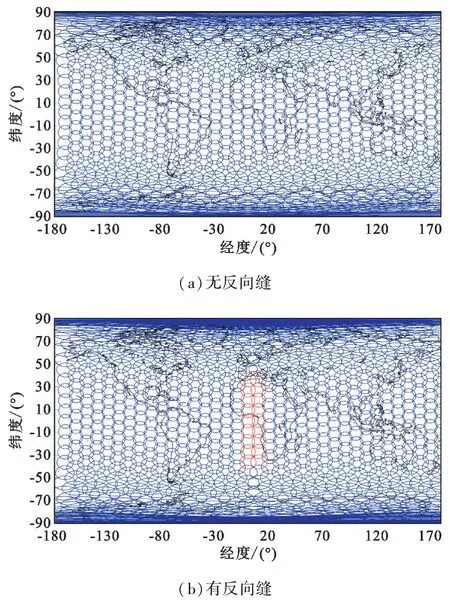
图2 低轨卫星全球有/无缝时的圆形覆盖
低轨卫星具有相对运动,在其首、尾轨道之间会产生动态的反向缝,在单个卫星的服务区为圆形的状态下,从图2(b)可以看出,反向缝两侧有部分区域未实现完全覆盖。如果单个卫星的服务区为椭圆,如图3(a)所示,要实现全球无缝覆盖卫星照射半张角在纬度方向为26.5°,在经度方向为37.1°。采用椭圆覆盖区进行全球排布后,如图3(b)所示,反向缝处也实现了无缝覆盖。

图3 低轨卫星全球有/无缝时的椭圆形覆盖
如果单个卫星的天线配置采用缝隙阵,缝隙阵天线能够形成纵向排列的长椭圆波束,利用多个长椭圆波束覆盖能够拼接成外包络近似为矩形的覆盖区域,即每个卫星的大覆盖区可以按矩形估计分析。当每个星在经度方向的半张角取为29°,纬度方向的半张角取25°时,单个卫星的服务区照射为矩形,可以产生如图4(a)所示的覆盖。采用这种缝隙阵天线形成的单星矩形服务区照射,也能够有效地解决单星服务区为圆形时反向缝区域的覆盖不足问题,如图4(b)所示。

图4 低轨卫星全球有/无缝时的矩形覆盖
3 不同形状的波束排布分析
从第2节的分析结果可以看出卫星在赤道附近的覆盖区交叠区域最小,本文选取赤道附近的相邻卫星进行卫星的子波束排布分析。
3.1 卫星椭圆覆盖下的波束排布
根据第2节的分析,当单个卫星的覆盖区域为圆形时,不能实现反向缝区域的完全覆盖,单个卫星覆盖区为椭圆和矩形时可以实现反向缝处的无缝覆盖。对于单个卫星的服务区为椭圆时,为了使得相邻卫星实现子波束完全覆盖,每个卫星都配置33个子波束,每个卫星的中间19个波束采用波束宽度为10.4°的圆波束,边缘14个波束采用波束宽度为9.7°的圆波束,每个卫星的配置相同。在波传输时,边缘波束的路径损耗要比中心波束的大,考虑到路径损耗,采用不等波束的排布可以实现波束的等增益照射[7]。从图5(a)可以看出,不考虑反向缝时,采用33个子波束的单个卫星的椭圆覆盖可以很好地实现全球无缝覆盖。但是,如果每个卫星的配置不变,还是33个子波束,如图5(b)所示,反向缝区域相邻卫星的子波束不能够很好地交叠。如果要实现反向缝区域的完全覆盖,就得增加单星的波束。通常为了批量化生产,会给低轨道星座的每个卫星配置一样的天线波束,如果反向缝处增加天线波束,在星座的其他运动时刻下势必会造成波束资源的浪费。因此这种单个卫星服务区采用椭圆覆盖的方法,表面上可以实现反向缝的完全覆盖,实际在进行子波束排布后发现,依然不能有效解决反向缝区域无法完全覆盖的问题。
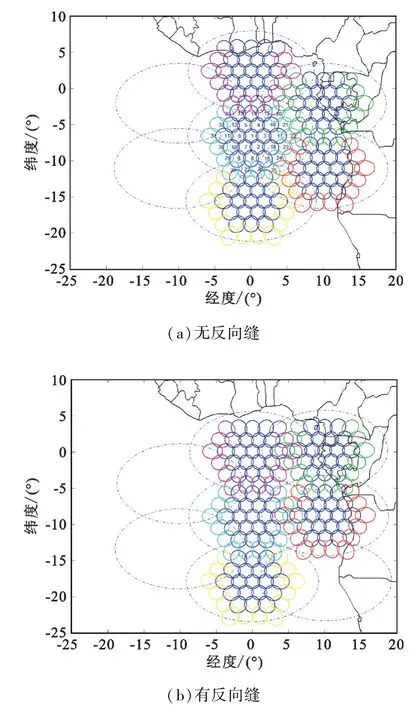
图5 椭圆覆盖区有/无反向缝时的波束覆盖
3.2 卫星矩形覆盖下的波束排布
为了解决反向缝区域无法完全覆盖的问题,考虑采用如图4所示的单个卫星矩形服务区覆盖。每个卫星配置16个波束宽度为58°×3.2°的长椭圆形波束,可以实现图4的一颗卫星矩形覆盖区的完全覆盖。并且采用这种波束的配置,如图6(a)所示,卫星的子波束配置采用长椭圆形波束实现了相邻同轨道卫星以及异轨道卫星的无缝覆盖,在反向缝情况下也可以实现无缝覆盖,如图6(b)所示。根据图5和图6有反向缝和无反向缝两种工况下卫星以及波束排布的情况可得表1。从表1以及前面的分析可知,采用矩形卫星覆盖以及波束排布设计既能保证反向缝区域的完全覆盖,也避免了波束过度重叠导致的资源浪费。
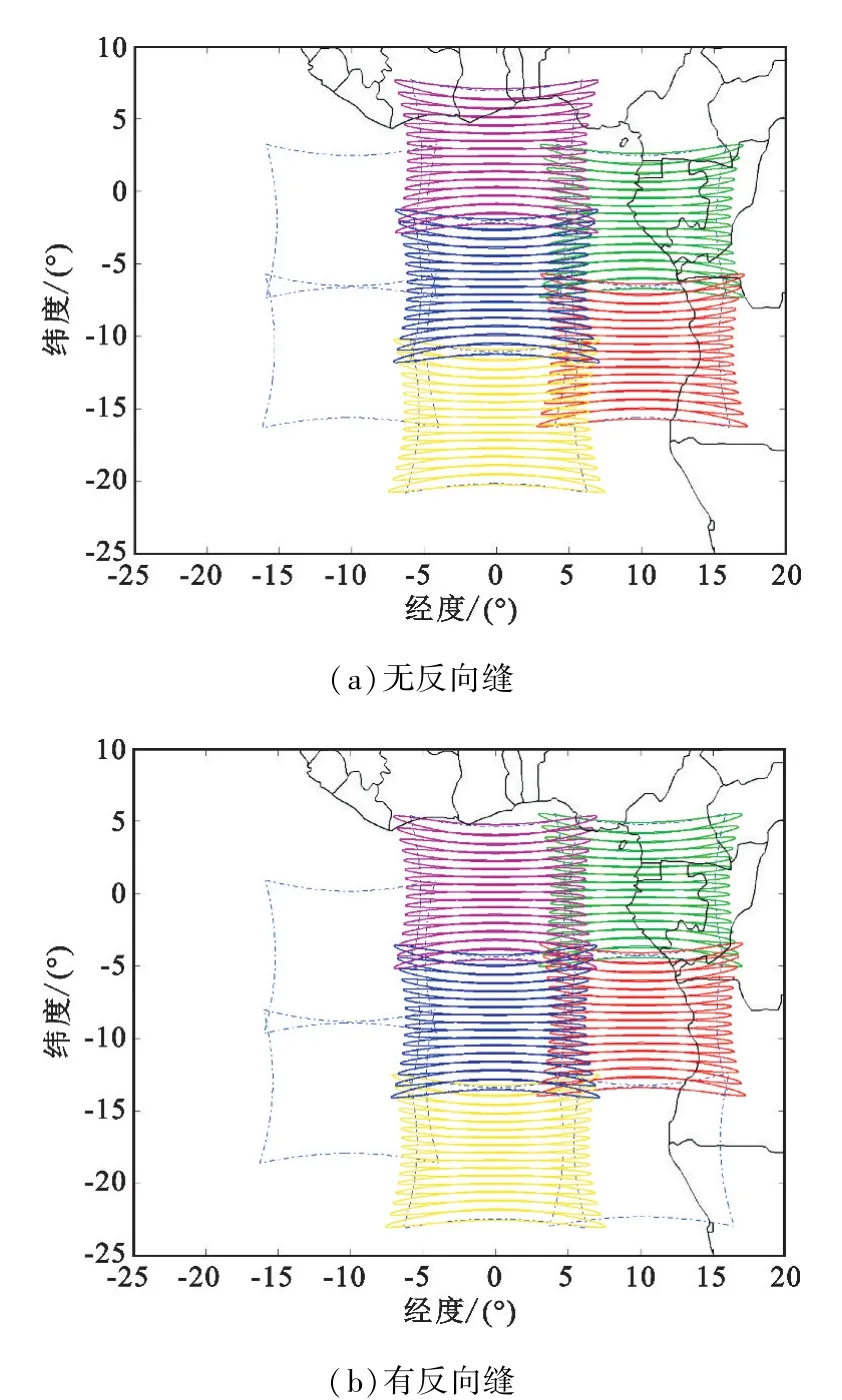
图6 矩形覆盖区有/无反向缝时的波束覆盖

表1 地球是否完全覆盖情况统计表
当低轨卫星星座的设计确定时,单个卫星波束的个数以及单个波束的性能取决于天线的实现能力,对于这种长椭圆形波束,缝隙阵天线可以很好地实现波束性能,缝隙阵天线的模型及辐射性能见第4节。
4 波束C/I分析
在卫星移动通信系统中,为了提高频率利用率,增加系统的容量,通常会采用频率复用的技术。同频干扰是指干扰信号与有用信号载频相同,会对接收同频信号的接收机造成的干扰。根据卫星波束复用关系以及各波束在地面上的电场分布可以计算复用波束在本波束的干扰功率。
4.1 C/I统计
假设卫星某个频率有n个同频波束,第i个波束在地面上的电场分布为Ei,则复用波束k对应的同频干扰值为
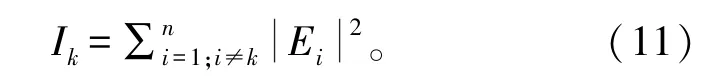
某频点波束k的载干比就可以用下式表示:
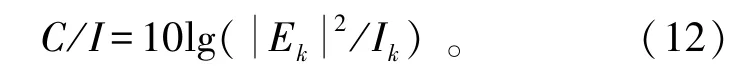
该根据分布场得到的载干比在地面上具有类似场一样的分布,根据波束宽度统计出最小C/I,可以得到波束k的载干比,统计n个波束的最小的C/I,便可知该频点的载干比。
变压器绕组的常见故障有径向变形、轴向位移以及内部匝间短路故障等。解体短路损坏的变压器发现,故障特征多表现为在故障电流所产生的轴向力和径向力的作用下,绕组扭曲、倾斜、坍塌和鼓包等永久性失稳变形。若不能及时发现,累积效应会使变形进一步加剧,进而导致绝缘损坏,出现匝间短路、饼间击穿、主绝缘放电等故障[10]。各种故障引起的绕组几何形状的任何变化都将导致图1所示的变压器等效电路的电容和电感元件发生改变。
如果n个同频波束中,波束还有极化复用,载干比还得考虑同频反极化的交叉极化分量的影响,比如n个同频波束,有m个波束是右旋极化,n-m个是左旋极化,假设k个波束是右极化,则在计算它的载干比时还需要考虑n-m个左旋极化波束的交叉极化分量的影响,因为这n-m个波束的交叉极化也是右旋极化。
假设卫星某个频率有n个同频波束,其中m个波束具有相反的极化,第i个波束在地面上的电场主极化分布为Ecoi,第j个反极化波束在地面上的电场交叉极化分布为Exj,则复用波束k对应的n-m-1个同频同极化的干扰值为
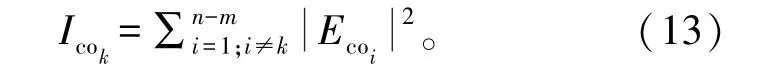
复用波束k对应的m个同频反极化的交叉极化的干扰值为

某频点波束k的载干比就可以表示为
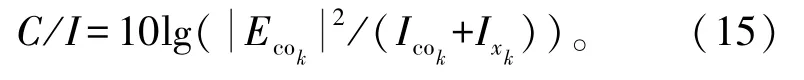
4.2 矩形覆盖下波束C/I
对于卫星的矩形覆盖,根据前面的分析,采用长椭圆形的波束进行波束覆盖,当所有的低轨卫星天线配置一样,在卫星运动时,可以在不改变单个卫星的波束个数情况下实现反向缝区域的完全覆盖,避免波束资源的浪费。图7给出了本文所采用的波导缝隙天线HFSS仿真模型。该模型中,通过在图7(b)的俯视图中馈电波导的上表面切割长度约为半波长的纵缝形成漏波,从而在波导的上表面形成电磁波辐射。波导上的每个缝隙为一个辐射单元,所有的辐射单元等幅同相馈电,形成等效的阵列天线辐射口面。沿电磁波辐射方向,每个辐射缝隙单元上方装配一个波导式圆极化器,该圆极化器由一个两面加脊、终端开路的方波导构成。为了实现矩形覆盖需求的波束宽度,本文设计了规模为1×24的波导缝隙阵列天线,其尺寸为330 mm×20 mm×29.8 mm,适合在小卫星上搭载。每个波导缝隙阵列天线的波束宽度为58°×3.2°,如图8(a)所示。为满足3.2节中对每颗卫星矩形覆盖区的要求,每颗卫星需要配置16个波导缝隙天线,其覆盖区沿卫星的飞行方向依次排布,并考虑一定的波束交叠,形成58°×50°的总覆盖区。在本文中,每个星只采用频率复用不采用极化复用方式,考虑到卫星资源的限制,波束采用四色频率排布。地面站天线方向图如图8(b)所示。

图7 缝隙阵天线模型

图8 天线方向图性能
采用图8(a) 的天线辐射场进行波束排布,根据公式(12)计算可得单星的C/I为23.69 dB,如果考虑极化复用,采用公式(15)计算。但是多频卫星同时工作时,以图6(a) 附近的卫星为例,每个星周围有6颗卫星,如果每颗星的波束配置一样,都采用图7所示的天线辐射场进行四色频率规划,对于周围6颗卫星的频率规划需要以中间卫星为参考,尽量减小对中间卫星同频区的影响,综合考虑后频率排布结果如图9所示。因为天线的辐射一般是在其安装的卫星坐标系下定义考虑的,对于多个不同的卫星,都有各自的坐标系,因此需要采用第1节的分析将UV坐标系下的天线场分布转化到经纬度坐标下之后,便可以采用公式(12)进行多颗卫星的能量叠加统计。计算得到中间星的C/I为-1.31 dB,远不能满足通信的需求,即便采用八色频率规划,统计计算得到中间星的C/I为5.63 dB,依然不能满足通信的需求。

图9 多星频率规划
4.3 地面站天线带指向下的C/I
以上考虑到周围六颗星对中间卫星的C/I影响的统计方法,未考虑地面站的方向性,因此统计C/I时,将地面站视场内卫星的所有波束能量进行了无差别积分。而实际上,地面站天线是定向天线,典型的地面站相控阵天线的辐射性能如图8(b)所示,其他卫星的同频区对于中间星的影响是只有其副瓣能量进入了中心卫星的波束覆盖区。因此在统计同频区能量的时候,需要考虑地面站天线的方向性。
对于跟踪扫描的情况,假设地面站天线一直对准中间卫星,可以根据周围6颗卫星跟中间卫星的空间位置关系,确定周围6颗卫星的波束能量和中间卫星波束能量的相对位置关系,从而可以确定周围其他6颗卫星进入到中间卫星同频波束区的能量值,再根据公式(12)或者公式(15)得出周围6颗卫星的同频区能量对于中间星的影响。通过计算可得,当地面站天线0°指向时,C/I为23.25 dB;当地面站天线30°指向时,C/I值为22.76 dB,满足一般通信对于C/I的要求。实际在计算波束C/I时,还要考虑低轨卫星的动态性,尤其在高纬度地区,首先要确定关星策略(已超出本文的研究的范围),在此基础上再进行波束的C/I分析。本文为动态的C/I分析提供了基本理论方法。
5 结 论
本文针对全球低轨卫星系统的动态性,讨论了单个卫星服务区为圆形、椭圆和矩形时的全球覆盖情况,并采用椭圆子波束排布对椭圆和矩形的卫星覆盖进行了仿真分析,给出了一种单个卫星矩形覆盖区采用波导缝隙阵的长椭圆子波束排布的方法。分析结果显示,该波束排布方法有效地解决了反向缝区域无法完全覆盖的问题,合理地利用了波束资源,为低轨卫星通信系统的波束设计提供了理论依据。

