能效最大化的无人机群三维部署策略分析*
董瑶瑶,王亚飞,姚媛媛,云 翔
(1.北京信息科技大学 a.信息与通信工程学院;b.现代测控技术教育部重点实验室,北京 100101;2.北京佰才邦技术有限公司,北京100101)
0 引 言
随着大规模数据流量的增加以及不可抗力因素如新冠疫情或者自然灾害的发生,无线通信系统快速、弹性部署的应急需求受到了学术界和工业界的广泛 关 注。近 年 来,无 人 机(Unmanned Aerial Vehicles,UAV)空地通信技术作为一种高效的解决方案,能够使得受损的地面无线网络得到快速恢复[1-2],例如辅助灾后区域恢复通信。同时,优化无人机的三维(3D)空间部署,可以大大提升用户的服务质量[3],给用户提供更低的延迟和更高的数据传输速率[4-6]。
无人机空中部署涉及到多维度变量以及复杂的空地(Air-to-Ground,ATG)路径损耗模型,根据实际需求动态部署无人机的三维空间位置以实现对地面用户的全覆盖,对于无人机应急通信场景的研究至关重要[7]。
由于单个无人机的服务能力始终受限,难以满足地面多用户的服务需求。以无人机群的组网形式,可以更好地发挥无人机作为空中基站的优势。文献[8]研究了部署多架无人机为有数据卸载需求的地面用户提供通信服务,结合K-means和模式搜索算法寻找最佳无人机位置,旨在最大化无人机网络的效益函数,同时提高无人机覆盖的用户数量;并且当用户数量增加,地面无线网络无法满足用户流量需求时,利用K-means算法优化多架无人机的3D位置,辅助用户进行数据卸载,能够有效提升网络容量[9]。
然而,传统的K-means算法对用户进行聚类的时候通常需要预先设定簇的数量。实际通信场景中,由于用户分布的随机性,加之影响通信的不确定因素较多,因此用户数量和所处环境往往是无法确定的,使用无人机辅助用户通信需要根据实际场景进行动态、智能部署。文献[10]构建了多无人机辅助地面智能设备的场景,并采用一种全局K-means算法优化无人机的2D水平位置,有效地减少了所需无人机数量,提高了网络能量效率。文献[11]提出了应急场景下的无人机快速部署方案,使用Kmeans和 连 续凸逼近(Successive Convex Approximation ,SCA)算法联合优化无人机的轨迹,旨在实现D2D(Device-to-Device Communication)用户的全覆盖,同时最大化系统吞吐量,但并未考虑无人机的高度优化,并且初始聚类集群的个数也是预先设定的,无法适用于复杂多变的通信环境。
考虑到地面用户的随机分布特性,为实现用户的全覆盖,同时避免出现冗余覆盖,本文提出了基于系统能效最大化的无人机群3D部署优化方案,主要创新点总结如下:一是将无人机3D部署位置解耦成2D平面部署和高度优化;二是为优化无人机的发射功率,提出了CT(Constrained Threshold)算法;三是为了衡量所提部署方案下的系统能效,定义了“集群能效函数(每个集群中用户端SINR总和/集群中主无人机的发射功率)”。理论分析和仿真结果表明,通过对无人机三维部署和发射功率的优化,所提策略能够大幅提升系统能效。
1 系统模型
如图1所示,当地面基站遭遇自然灾害无法正常工作时,通过部署无人机作为空中基站,能够为地面用户快速搭建通信链路。图1(a)所示为无人机群定高飞行下等半径覆盖的部署情况,对于随机分布的地面用户,很难实现全覆盖。图1(b)中所提无人机优化部署方案,可以根据实际通信环境动态改变飞行高度以实现用户的全覆盖。

图1 多无人机部署模型
考虑无人机群在下行链路中辅助地面用户通信。将无人机群记为j={1,2,3,…,J},无人机的发射功率集合使用P={pj}表示,高度集合记为H={hj},(Xj,Yj)表示无人机j的水平位置。其中用户随机分布于矩形区域A中,用户的数量记为Ni={1,2,3,…,NI},使用(xi,yi)表示用户i的坐标。
无人机与用户之间通信的规则如下:每个用户i只能接入一个无人机j进行通信,所连接的无人机称为主无人机。而每架无人机能够同时辅助多个用户进行通信,由于无人机的通信资源有限,所能支持的用户数量NU∈[Nmin,Nmax],Nmin表示所能支持的最小用户数量,Nmax表示所能支持的最大用户数量。使用κi,j表示用户i与无人机j之间的连接关系,

1.1 ATG信道模型
为了捕获由于障碍物引起的信号失真,采用基于概率的路径损耗模型。ATG路径损耗表示如下[12]:
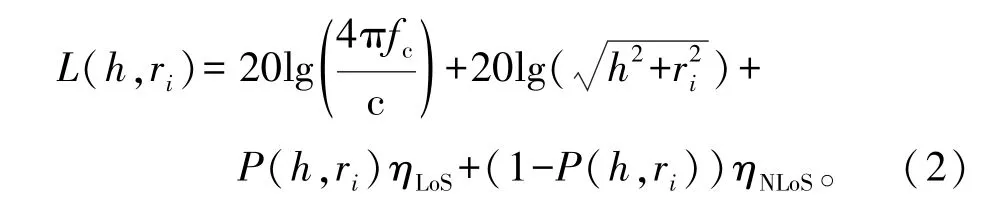
式中:h表示无人机的高度;ri代表用户i与无人机在地面投影点之间的水平距离;fc表示载波频率;c表示光速;ηLoS是视距链路(Line of Sight,LoS)的额外损耗,ηNLoS是非视距链路(Non-line-of-Sight,NLoS)的额外损耗。视距链路的概率表达式为

式中:θ=h/ri是无人机的俯仰角度;a和b是取决于环境的常量。由公式(3)可知,视距链路和非视距链路的概率取决于无人机的高度,以及无人机和用户之间的仰角。
1.2 问题建模
为了实现对地面用户的全覆盖,同时优化无人机的发射功率以降低系统能效,使用MCK算法优化无人机的二维平面部署,并通过最小化ATG路径损耗获取无人机的最佳高度;最后利用CT算法优化无人机的发射功率。接下来,为衡量上述所提方案对系统能效的影响,定义了集群能效函数(即每个集群中用户端SINR总和/主无人机的发射功率),具体公式如下:

式中:Cj表示MCK部署后第j个无人机所在的集群编号;μCj表示集群Cj的能效;表示聚类到集群Cj的用户数量;表示优化后的用户端接收SINR;表示集群Cj中优化后的无人机发射功率。
根据上述研究场景,相应的优化问题由下式给出:

其中,约束(5b)表示接入无人机的用户数量Ni不超过无人机自身所能支持的最大用户数Nmax;约束(5c)和(5d)确保每个用户只能连接至一个无人机;USINRe是无人机覆盖集群内边缘用户端所接收到的信干噪比;S表示用户端SINR最低阈值;约束(5e)保证了用户端的服务质量约束;约束(5f)表示无人机的发射功率最大值约束,即不能超过Pu。
目标优化问题旨在通过优化无人机的3D空间部署,实现用户的全覆盖;同时在保证用户的QoS下,通过最小化无人机的发射功率,最终使得系统能效最大化。
系统相关符号含义如表1所示。

表1 系统符号表
2 无人机3D部署
无人机3D位置部署可以解耦成2D平面部署和高度优化[12]。
2.1 MCK算法优化无人机2D部署
假设无人机与其覆盖区域内的用户之间的路径损耗上限为Lmax,此时所对应的用户位于无人机覆盖区域的边缘,即对应无人机的最大覆盖半径,记为Rm。
2.1.1 初始化无人机2D位置
K-means初始化方法使用最近邻重心策略将地面用户划分为不同的集群,并初始化每个集群的中心,即无人机的水平坐标。同一集群中的用户具有最大的相似性并且不同的集群中的用户相似度较低。根据最小路损接入准则,用户i关联到相应的无人机j,即
(Xk,Yk)表示集群中其他无人机k的水平位置坐标,则用户i关联的无人机j的水平坐标可表示为

2.1.2 更新无人机2D位置
当用户初始聚类完成以后,约束条件为
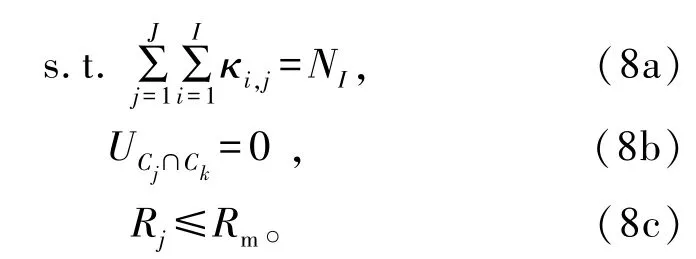
式中:UCj∩Ck表示集群Cj和Ck重叠区域的用户数;约束(8a)确保每个用户都能够被覆盖;约束(8b)表示重叠区域内不存在用户;约束(8c)表示每架无人机覆盖半径Rj不能超过Rm。根据约束条件(8a)~(8c),当算法不满足以上约束条件中的任何一个时,增加集群的个数,重新对用户进行聚类并计算更新后的无人机坐标:
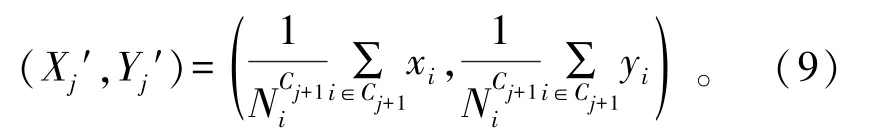
根据以上分析,完成无人机的2D坐标部署后,获取每架无人机覆盖区域的最大半径RCj。
2.2 无人机垂直高度优化
本节将优化无人机的垂直高度。根据2.1节所获取的每架无人机的最大覆盖半径RCj,以及ATG路径损耗函数L(h,RCj)确定无人机的最佳高度h*。
定理1:如果已知无人机的覆盖半径R0,通过最小化ATG路径损耗函数,可以得出无人机的最佳高度。
证明:由公式(2)可知,路径损耗函数是连续的,因此可以得到

如果h1<h2,那么存在局部最小值h0∈[h1,h2]。对公式(2)进行求导,有以下
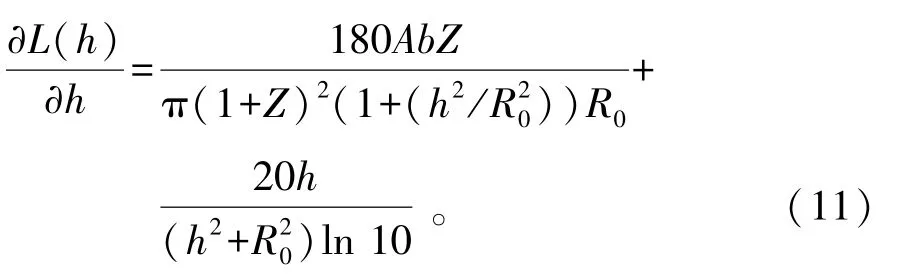
式中:
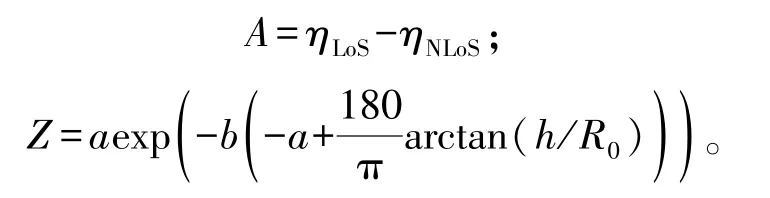
接下来令h1=R0/2,h2=R0,无人机服务的场景设定为Urban[13],因此,a=9.61,b=0.16,ηLoS=1,ηNLoS=20。将数值代入公式(11),有
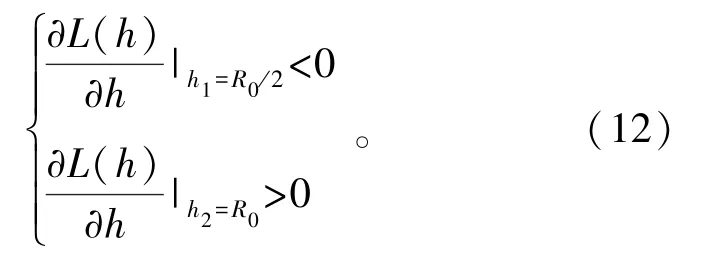
由公式(10)可知,存在局部最小值h0∈[R0/2,R0],使得ATG路径损耗最小。
定理2:如果存在最佳高度h*使得ATG路径损耗函数最小,则h*是唯一的。
证明:首先,arctan(h/R0)函数是单调的,由θ(h)=arctan(h/R0)可知,最佳角度θ*对应最佳高度h*,即

从定理1中可以知道,局部最小h*存在,故有θ*=arctan(h*/R0),并且。进而可以得出[4],当
综上所述,在无人机的覆盖半径已知的情况下,通过最小化路径损耗函数,无人机的最佳高度h*存在且唯一。将记为每个集群中的无人机j最佳高度。
2.3 无人机3D最佳部署
MCK(Modified Constraint K-means)算法优化2D平面部署,通过最小化路径损耗函数获取无人机最佳高度。接下来给出无人机群的三维最佳部署算法的伪代码:
输入:用户的位置:(xi,yi),无人机最大覆盖半径Rm,每个无人机所能允许接入的最大用户数量Nmax。
输出:每架无人机的3D坐标:(Xj,Yj,h*Cj)。
初始化:
1 WhileUCj∩Ck=0 do
2 使用MCK将用户聚类到j个无人机中
3 获取每个无人机的覆盖半径RCj
4 获取每个无人机覆盖区域中的用户数量
5 动态调整覆盖半径RCj,保证,同时RCj<Rm
6 else
7j=j+1
8 通过最小化无人机与各自集群中用户之间的路径损耗,获取无人机最佳高度h*Cj。
9 获取每架无人机的3D坐标(Xj,Yj,h*Cj)
10 end While
3 最大化系统能效
计算每架无人机覆盖区域中边缘用户i的SINR表达式,取对数后表示如下:
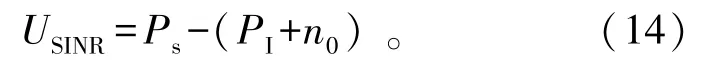
式中:Ps指用户i接收到的来自主无人机传输的信号功率;PI指用户i接收来自集群外干扰无人机传输的信号功率;n0表示信道噪声功率。Ps和PI分别表示如下:
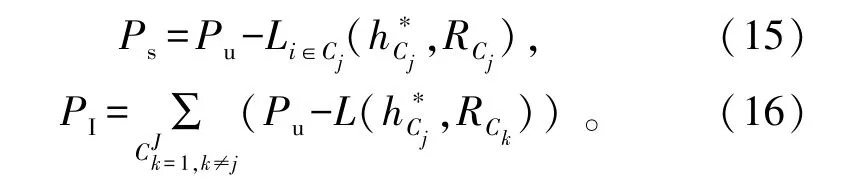
式中:Pu是无人机的发射功率;表示用户i与主服务无人机的通信路径损耗rCk)表示用户i与干扰无人机之间的路径损耗。根据已知无人机最佳高度h*以及最大覆盖半径RCj,由公式(2)可计算得出无人机与用户i之间的的路径损耗,进而可以得出边缘用户i接收端的SINR。
为满足用户端的QoS,CT算法通过检测边缘用户接收信号的SINR,不断优化无人机的发射功率,直到。其中,ε是误差精度,S表示SINR阈值。
CT算法的伪代码如下:
输入:边缘用户的位置(xi,yi),每架无人机最佳高度,每架无人机最大覆盖半径RCj,无人机发射功率Pu。
输出:优化后每架无人机发射功率:。
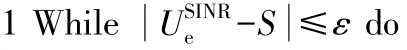
2 forj=1:J
3 计算主服务无人机与边缘用户的路径损耗Li∈Cj(h*,rCj)
4 fork=1:J
5 ifk≠j
7end
8 end
9 end
10 根据公式(14)计算边缘用户的SINR
11 降低主服务无人机发射功率,记为
12 根据公式(14)更新边缘用户的SINR
13 end While
根据优化后的无人机发射功率,结合公式(14)求出每个集群中所有用户的SINR,并将优化后的无人机发射功率代入公式(4),最终计算得出系统能效。
4 仿真与分析
为了验证所提方案的有效性,通过仿真对系统性能进行评估。地面用户的初始位置是随机分布在2 000 m×2 000 m的地理区域中。系统各个参数在表2中给出。同时,为了更好地说明所提算法对于系统能效提升的有效性,对比了以下几种方案:

表2 系统参数
(1)MCK_Heightonly:表示MCK部署下,仅有无人机的高度优化,但是没有对无人机的发射功率进行优化。
(2)MCK_Poweronly:表示MCK部署下,仅有无人机的发射功率优化,但是没有高度优化。
(3)MCK_CT:表示MCK部署下,采用CT算法,既考虑了无人机的发射功率优化,也考虑了无人机垂直高度优化。
图2给出了不同算法下的无人机群部署情况,假设用户数取60。由图2(a)可见,传统K-means部署无法保证用户全覆盖,并且容易出现用户冗余覆盖的情况;图2(b)使用所提的MCK算法对无人机进行部署,在K-means的基础上增加约束条件能够弥补K-means的不足。从图中还可以看出,用户不仅实现了全覆盖,并且重叠区域内不存在冗余用户。
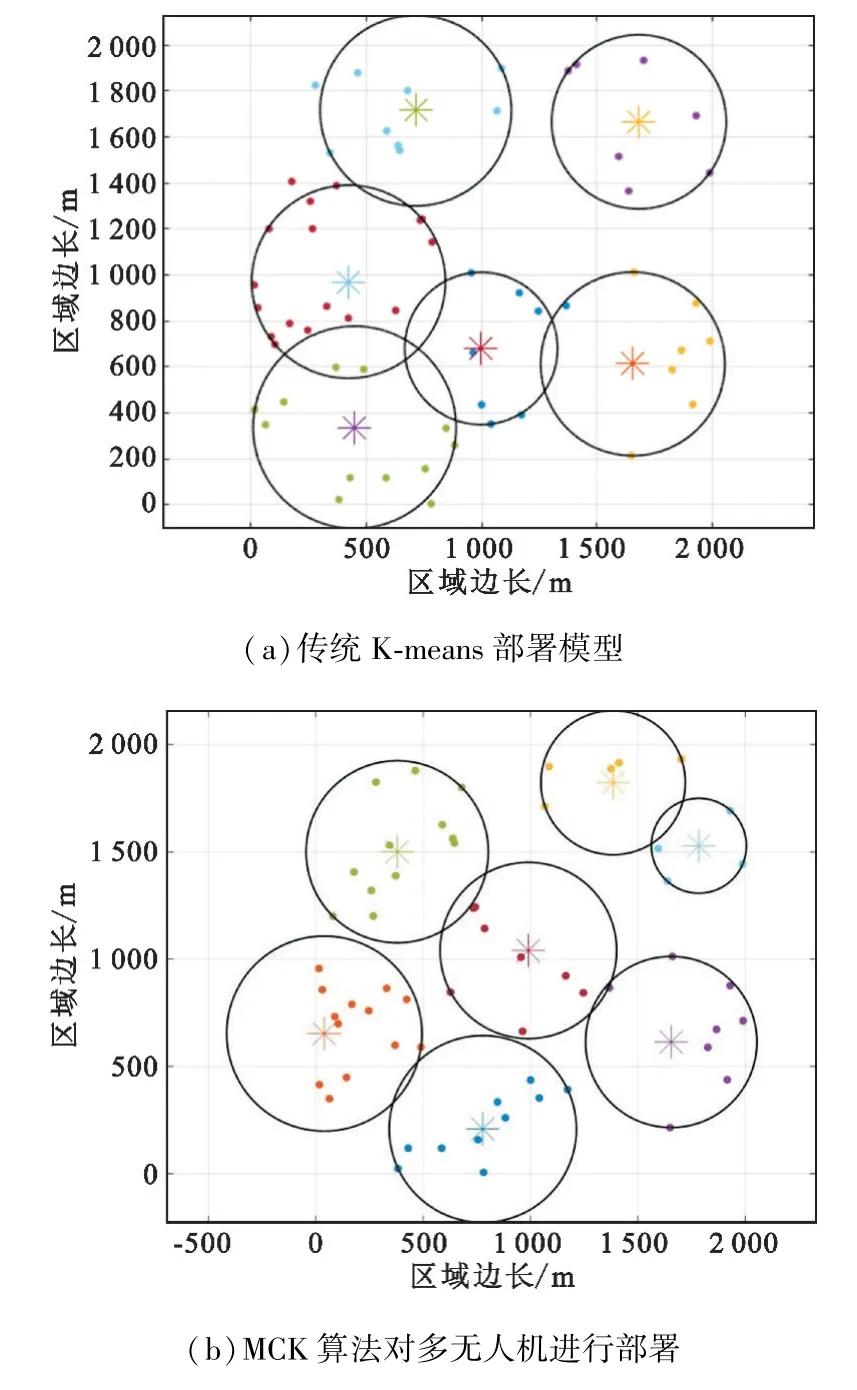
图2 不同算法下的无人机群部署情况
从图3可以看出,当用户数量分别为80、100时,使用MCK算法对无人机进行部署可以实现对地面用户的“零冗余全覆盖”。对于不同的场景,由于用户数量以及分布都是随机的,所以无人机的部署数量无法预设,并且每架无人机的覆盖半径也必须根据实际的需求进行动态调整。MCK算法能够适用于复杂多变的实际部署场景,并且具有较强的灵活、弹性部署特性。
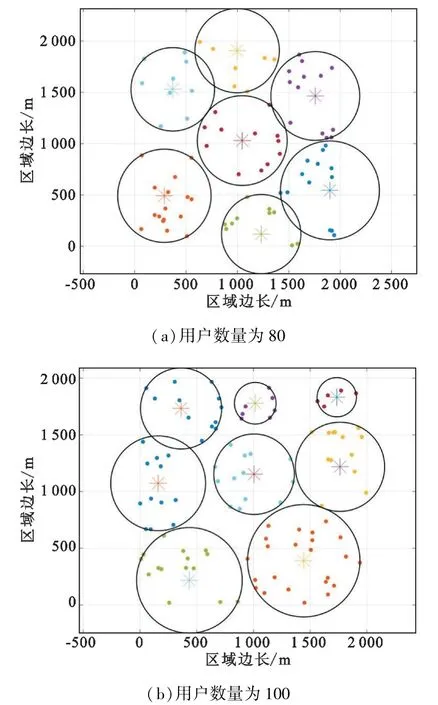
图3 MCK算法下无人机群部署情况
图4给出了无人机的优化高度和无人机覆盖半径之间的关系。获取每架无人机的覆盖半径后,由定理1以及定理2可知,通过最小化路径损耗函数可以得到无人机的最佳高度,最佳高度存在局部最小值h0∈[R0/2,R0],因此无人机的高度与无人机的覆盖半径成正比关系,半径越大,高度越高,与图4的仿真结果保持一致。

图4 无人机高度优化
图5给出了CT算法优化无人机发射功率的仿真结果。根据算法流程,当满足收敛条件即时输出最终的无人机发射功率。从图中可以看出,相较于优化前,优化后的无人机发射功率大大降低。另外,从图5也可以看出每架无人机的发射功率降低百分比。仿真结果表明所提算法能够很大程度降低无人机的发射功率,节省了无人机的额外能耗,延长了无人机网络的生命周期。

图5 无人机功率优化
图6给出了系统能效对比结果,从图中可以看出,相比于MCK_Heightonly以及MCK_Poweronly方案,MCK_CT算法联合优化无人机的3D空间部署和发射功率能够大幅提升系统能效。这是因为优化无人机的高度能够减小无人机与用户之间的路径损耗,增加用户端的SINR,优化无人机的发射功率能够在确保用户端的QoS条件下降低无人机的发射功率,节省无人机的额外能耗,再结合公式(4),联合无人机群3D部署和功率优化,对于系统能效的提升有显著的作用。同时图6中对比了MCK_Poweronly和MCK_CT两种算法,可以看出在MCK_CT算法下系统能效提升百分比。仿真结果表明所提算法能够大幅提升系统能效。
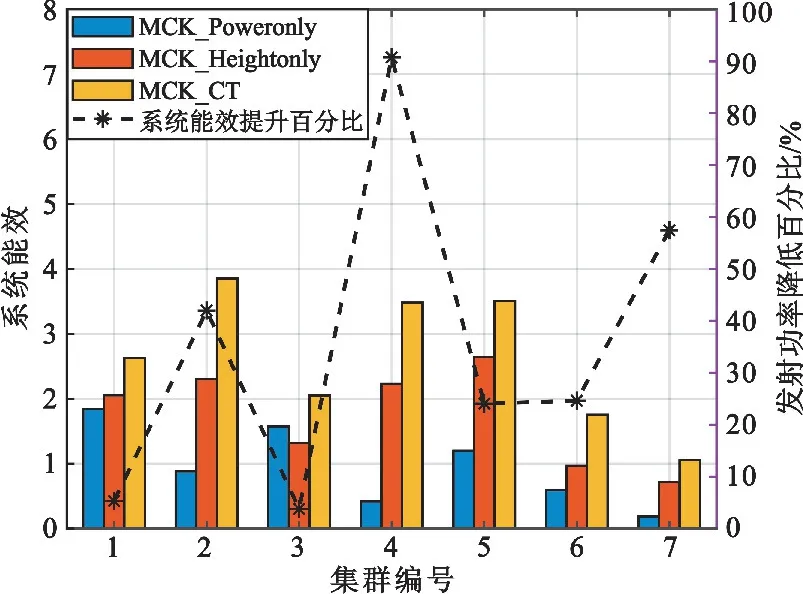
图6 系统能效对比结果
5 结束语
本文针对无人机辅助灾后区域应急通信场景的问题,提出了最小化无人机能耗的3D空间部署方案,以实现用户的全覆盖,并提升系统能效。首先利用MCK算法优化无人机的2D水平位置,然后通过最小化路径损耗函数获取无人机群的最佳高度,最后使用CT算法优化无人机的发射功率以提升系统能效。该研究对于无人机应急通信场景下系统性能提升具有一定的指导意义。下一步重点关注实际通信场景中的随机衰落和小尺度衰落,对空地信道进行更为全面的分析。

