用于资源动态预留的航天测控资源配置优化算法*
梁 军,陈学军,刘建平,原东阳,罗清青
(西安卫星测控中心,西安 710043)
0 引 言
航天测控设备是航天测控网的主要组成部分,在日常运行中承担着对航天器进行跟踪测量、遥测、遥控和通信等测控任务[1]。随着在轨航天器数量的不断增加,对航天测控资源的需求迅速增多,航天器测控需求的类型也变得越来越多样化,给测控系统带来越来越大的压力,在一定条件下能为在轨航天器提供支持服务的容量也是有限的[2-3]。
在航天器数量和航天器任务需求增加的条件下,测控需求与航天测控资源可提供的服务能力之间的矛盾不断增加[4]。由于航天测控设备建造和维护成本较高,如何经济、科学和合理地配置航天测控资源,对测控设备进行最优调度进而提高地面设备的使用率[5],充分发挥航天测控资源效益和最大限度地满足各类航天器任务的需要,是一个迫切需要研究解决的重大问题[6-7]。航天测控资源的配置优化问题主要是研究如何针对现有的航天器测控需求合理地配置一定数量的航天测控资源,通过寻找最优的配置方案使用户预期的目标函数达到最优化[8-9],进而提升航天测控设备的整体运行效能,保障更多的航天测控需求,以解决当前航天测控资源紧张的问题。
近年来,围绕不同问题领域中的资源高效配置和优化问题,国内外学者对其建模和求解方法进行了一些研究[10-12],但是并没有考虑资源动态预留情况下的资源配置优化。为此,本文着重在考虑资源动态预留的情况下进行航天测控资源配置优化问题的建模和求解。本文立足于航天器用户方的测控需求满足率最大化的目标和航天测控设备管理方的测控设备利用率最大化的目标,建立了能在国内东部、西部、南部和北部四大测控区域中更加均衡地预留出更多、更重要的设备的航天测控资源配置优化模型,进而提出基于可回溯的并行最佳优先搜索的航天测控资源配置优化算法,实现了在以日计划形式进行的航天测控资源周期调度中资源动态预留的预期效果,为在航天测控资源调度过程中优化提升航天测控设备的服务能力奠定了理论基础。
1 问题描述
航天测控资源配置优化问题属于组合优化问题,但又比经典的组合优化问题求解困难,主要是因为该问题的约束条件繁杂且数量众多,目标函数的组成成分多样且在优化过程中呈现出不确定性。航天测控资源配置优化问题主要解决的是如何给地面站配置设备,使得配置方案的综合效能最好,包括地面站点位的选址和航天测控设备配置数量的优化等。
在实际中,地面站点位的选址要受到地形、当地气候、政治条件以及航天器用户方的需求等诸多因素的影响,在具体实践中一般要对地面站点位的选址进行单独的研究论证。因此,本文中航天测控资源配置优化问题主要研究的是在满足航天器用户方提出的全部任务需求的前提下,如何在现有的航天测控设备集合中选择数量尽可能少的设备来为所有任务需求配置可用的服务时间窗口,通过寻找最优的配置方案来使既定的目标函数达到最优化。例如,假定航天测控设备集合中有J套设备(即SD={D1,…,Dj,…,DJ}),在满足所有任务需求的情况下,设备集合SD中参与任务的设备所组成的子集合(即SE={D1,…,De,…,DE},E≤J)以及相应的服务时间窗口集合(即SW={W1,…,We,…,WE},We为第e套参与任务的设备De上执行的服务时间窗口集合),则为航天测控资源的一种配置方案,配置优化的目标就是在航天测控设备集合中寻找能使目标函数达到最优的一种配置方案。因此,航天测控资源配置优化问题中涉及到的输入、输出和优化目标等相关要素描述如下:
(1)输入要素:给定调度周期;给定低轨航天器需求型任务集SR;给定航天测控设备集SD,以及每个需求型任务Rg的可支持设备列表Lg;给定每个需求型任务Rg的航天器对其可支持设备列表Lg中所有设备的星地可见预报,并形成需求型任务Rg的备选可用弧段集。
(2)输出要素:参与任务的航天测控设备集合以及数量;为每个需求型任务Rg进行保障的设备和服务时间窗口的配置方案。
(3)优化目标:对于航天器用户方而言,最大程度地提高任务需求的满足率;对于航天测控设备管理方而言,最大程度地提高设备利用率,进而给一些关键任务在国内东部、西部、南部和北部四大测控区域中更加均衡地预留出更多、更重要的设备。
2 航天测控资源配置优化模型建立
2.1 原子型任务的形式化描述
地面站原子型任务(以下简称原子型任务)是指地面站根据航天器用户方提出的低轨任务需求对航天器进行单次保障服务,这样就将航天器用户方提出的低轨任务需求转化为若干个相互之间存在着关联约束的原子型任务。因此,原子型任务集是指多个原子型任务组成的集合,表示为SA={A1,…,Ai,…,AI},Ai∈SA为第i个原子型任务,I为原子型任务的数量。其中,单个原子型任务A可采用公式(1)所示的8元组进行规范化描述,式中每个元素的含义如表1所示。


表1 原子型任务中8元组含义及描述
2.2 优化模型建立
航天测控资源配置优化问题是多类且大量约束并存的、资源高度冲突的组合最优化问题。航天测控资源配置优化模型是对航天测控资源配置优化问题的数学描述,也是设计求解方法的基础。本节将分析航天测控资源配置优化过程中的决策变量、约束条件和目标函数等建模要素,从而构建出航天测控资源配置优化模型。
2.2.1 决策变量
航天测控设备对航天器星地可见预报的一个备选可用弧段定义为
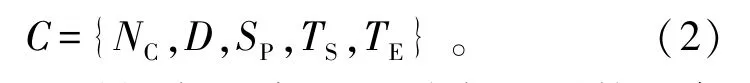
式中:NC为可用时间窗口编号;D为航天测控设备代号;SP为航天器代号;TS为开始时刻;TE为结束时刻。
对于原子型任务集SA中的第i个原子型任务Ai而言,其备选可用弧段集为Bi,备选可用弧段的总数为Hi。其中,第i个原子型任务在航天测控设备集SD中的第j个可支持设备Dj上执行的第k个备选可用弧段Ck属于子集Bij(Bij⊆Bi),该集合中备选可用弧段的个数为Hij(Hij≤Hi)。因此,决策变量定义为

2.2.2 约束条件
(1)原子型任务执行的唯一性约束
原子型任务执行的唯一性约束是指每个原子型任务最多只能执行一次。这是由于能够为每个原子型任务提供任务保障的航天测控设备有多个,每个原子型任务具体在哪个设备的哪个可用时间窗口上执行是一个可以选择的过程。只要为原子型任务选定一个可用时间窗口,该原子型任务即被成功调度,重复执行同一个原子型任务会造成航天测控设备的资源浪费,可能导致无法保障其他原子型任务的完成。
用决策变量表示这种类型的约束就是每个原子型任务对应的决策变量的取值最多为1,如式(4)所示:

(2)航天测控设备执行任务的唯一性约束
①每个航天测控设备在执行一个原子型任务的过程中不执行其他的原子型任务。
②每个航天测控设备在执行一个原子型任务时需要满足设备状态的转换时间。
③每个航天测控设备在一个调度周期内(本报告中为一天)有最大期望负荷率约束。
根据对地面站测控过程的描述可知,航天测控设备所处的捕获时间段和跟踪时间段称为测控任务持续时间,必须在可用时间窗口内;而航天测控设备所处的准备时间段和释放时间段称为设备转换时间,可以在可用时间窗口内,也可以不在可用时间窗口内。
将航天测控设备的准备时间、捕获时间、跟踪时间和释放时间统称为非空闲时间,则航天测控设备执行任务的唯一性约束中的①和②重新表述为:当航天测控设备处于非空闲时间段时,不能为其他原子型任务提供保障服务,只有航天测控设备再次处于空闲时间段时,才能为新的原子型任务提供保障服务,如图1所示。

图1 航天测控设备执行任务的唯一性约束示意图
为了方便描述航天测控设备可执行弧段冲突集的生成算法,首先需要定义航天测控设备可执行弧段这一数据结构。一个航天测控设备的可执行弧段E是在该航天测控设备的一个可用弧段C的基础上加上该航天测控设备的准备时间和释放时间而产生的,定义如下:

式中:TES为可执行弧段的开始时刻;TEE为可执行弧段的结束时刻;tES为该可执行弧段所属的航天测控设备的准备时间;tER为该可执行弧段所属的航天测控设备的释放时间。
从图1可以看出,对于一个原子型任务而言,由第j个航天测控设备Dj上的第e个备选可用弧段Ce,便可生成该航天测控设备保障这个原子型任务的一个可执行弧段Ee。其中,该可执行弧段的开始时刻和结束时刻的计算公式如(6)所示:
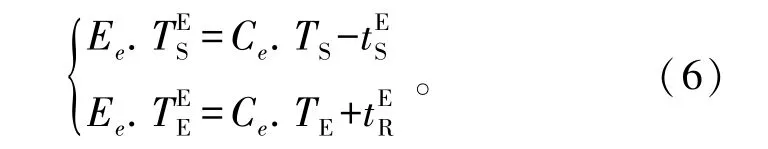
由此可知,第j个航天测控设备Dj从第e个可执行弧段Ee的开始时刻TES到结束时刻TEE,该航天测控设备只能执行一个原子型任务,TES到TEE之间的时间段就是第j个航天测控设备的非空闲时间。
因此,如果用决策变量X来表示航天测控设备执行任务的唯一性约束①和②,则为在第j个航天测控设备Dj上的第e个可用弧段Ce的可执行弧段冲突集Wje中,最多只有一个可用弧段能被用来调度。

式中:Ek是可执行弧段冲突集Wje中在第j个设备Dj上执行的第k个可执行弧段;K是可执行弧段冲突集Wje中可执行弧段的个数。
在调度周期内第j个航天测控设备Dj的任务执行总时长为因此,航天测控设备执行任务的唯一性约束③可描述为

式中:是第j个航天测控设备Dj在一个调度周期内的最大任务负荷量(也就是该设备在调度周期内的所有可见预报取并集的时长);是第j个航天测控设备的最大期望负荷率。
(3) 航天器执行任务的唯一性约束
①每个航天器在执行一个原子型任务的过程中不能执行其他原子型任务。
②每个航天器在执行升降轨类型相同的多个原子型任务的过程中,需要满足该航天器低轨需求型任务中的最小、最大间隔时间要求,并且升降轨类型相同的多个原子型任务被调度的可用弧段所属的圈次应该不同或者连续。
③每个航天器在执行相邻的升轨和降轨原子型任务的过程中,需要满足该航天器低轨需求型任务中的相邻升降轨最大间隔时间要求。
如图2所示,航天器执行任务的唯一性约束可理解为:对于属于同一个航天器且升降轨类型相同的两个原子型任务,当前原子型任务执行的持续时间和该原子型任务执行完毕后持续到最小间隔时间以及最大间隔时间以后的时间段,该航天器均处于非空闲状态,不能再执行与该原子型任务属于同一个航天器且升降轨类型相同的其他原子型任务;对于属于同一个航天器但升降轨类型不同的两个原子型任务,当前原子型任务执行的持续时间以及该原子型任务执行完毕后持续到最大间隔时间以后的时间段,航天器均处于非空闲状态,不能再执行与该原子型任务属于同一个航天器但升降轨类型不同的其他原子型任务。

图2 航天器执行任务的唯一性约束示意图
为了方便描述航天器可执行弧段冲突集的生成算法,首先需要定义航天器可执行弧段这一数据结构,如式(9)所示。航天器的一个可执行弧段Z是在可用弧段C的基础上加上该航天器低轨任务需求中的相同升降轨类型中的最小间隔时间、最大间隔时间和不同升降轨类型中的相邻升降轨最大间隔时间而产生的。
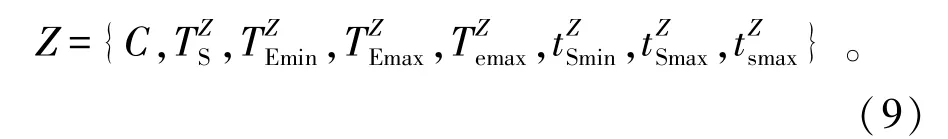
式中:TZS为可执行弧段的开始时刻;TZEmin为可执行弧段的最早结束时刻;TZEmax为可执行弧段的最晚结束时刻;TZemax为可执行弧段的相邻升降轨最晚结束时刻;tZSmin为低轨任务需求中相同升降轨类型的最小间隔时间;tZSmax为低轨任务需求中相同升降轨类型的最大间隔时间;为低轨任务需求中相邻升降轨的最大间隔时间。
从图2可以看出,由航天器低轨需求型任务集SR中第g个需求型任务Rg上的第e个可用弧段Cge,可生成一个可执行弧段Zge。其中,可执行弧段的开始时刻和结束时刻的计算如公式(10)所示:
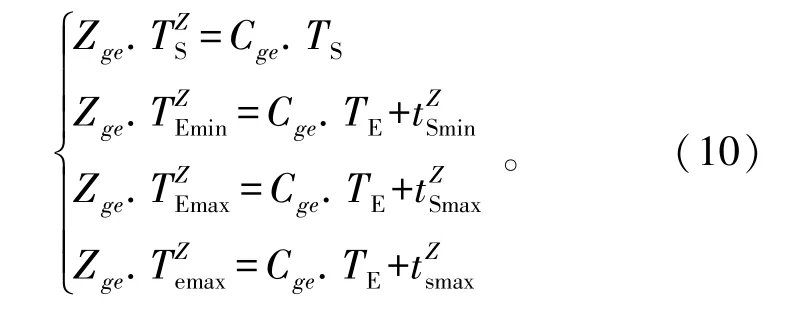
由此可知,在第g个需求型任务Rg上的第e个可执行弧段Zge的开始时刻到最早结束时刻
之间的时间段以及最晚结束时刻以后的时间段内,该航天器都不能再执行与该可执行弧段具有相同升降轨属性的其他原子型任务。因此,到之间的时间段以及以后的时间段均为该航天器执行与第e个可执行弧段Zge具有相同升降轨属性的原子型任务的非空闲时间。在第g个需求型任务Rg上的第e个可执行弧段Zge的相邻升降轨最晚结束时刻以后的时间段内,该航天器都不能再执行与该可执行弧段具有不同升降轨属性的其他原子型任务。因此,以后的时间段均为该航天器执行与第e个可执行弧段Zge具有不同升降轨属性的原子型任务的非空闲时间。
因此,如果用决策变量X来表示航天器执行任务的唯一性约束①和②,则为在第g个需求型任务Rg上的第e个可用弧段Cge的具有相同升降轨属性的可执行弧段冲突集Vge中,最多只有一个可用弧段能被用来调度。

式中:Ck是可执行弧段冲突集Vge中第k个可用弧段;K是可执行弧段冲突集Vge中可执行弧段的个数;Ig是航天器低轨需求型任务集SR中第g个需求型任务Rg的原子型任务的个数。
同理,如果用决策变量X来表示航天器执行任务的唯一性约束③,则为在第g个需求型任务Rg上的第e个可用弧段Cge的具有不同升降轨属性的可执行弧段冲突集Uge中,最多只有一个可用弧段能被用来调度。
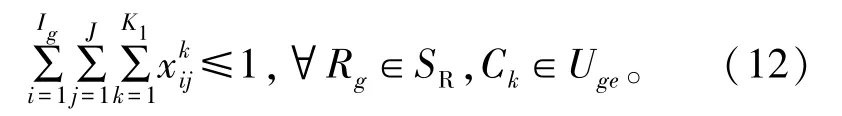
式中:Ck是可执行弧段冲突集Uge中第k个可用弧段;K1是可执行弧段冲突集Uge中可执行弧段的个数。
2.2.3 目标函数
以原子型任务的备选可用弧段作为航天测控资源配置优化问题的决策变量后,该优化问题的求解就转化为在决策变量集合X中选择一组满足各项约束条件并能使目标函数值最优的决策变量。其中,对于航天器用户方而言,航天测控资源配置优化的目标函数是最大程度地提高低轨任务需求的满足率;对于航天测控设备管理方来说,航天测控资源配置优化的目标函数就是最大程度地提高设备利用率,进而给一些关键任务在国内四大测控区域中更加均衡地预留出更多、更重要的设备。
(1)航天器用户方的目标函数
由于航天测控设备的可见时间窗口资源有限,航天器用户方希望提出的低轨任务需求能最大程度得到满足,即最大化低轨任务需求满足率。当低轨任务需求转换为原子型任务之后,低轨任务需求满足率就转换为原子型任务满足率。原子型任务满足率是成功调度的原子型任务的总收益值与低轨任务需求所要求的原子型任务的总收益值之间的比率。在航天测控资源优化配置过程中,不但要尽可能多地完成原子型任务,还要尽可能完成优先级高的原子型任务。其中,低轨航天器用户方给定低轨任务需求后,原子型任务的总收益值就是一个常量,表示为其中是第i个原子型任务Ai的优先级。因此,原子型任务满足率表示为
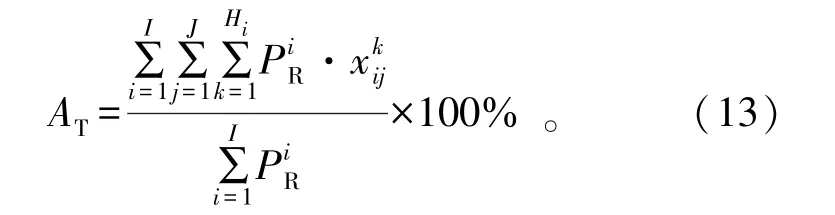
式中:J是指航天测控设备集SD中设备的个数。另外,如果原子型任务满足率为100%,这说明所有任务均能完成,这时就无需考虑不同任务的优先级高低对任务满足率的影响。
(2)航天测控设备管理方的目标函数
对于航天测控设备管理方来说,在航天测控资源优化配置的目标函数中,首先需要最大化航天测控设备的负荷率,也就是相当于最小化参与任务的设备数量;其次需要使设备集合中未参与任务的预留设备的重要程度越高越好,也就是相当于最大化预留设备的重要性指标;最后尽可能使预留设备在国内四大测控区域中能够均衡分布,也就是相当于最大化预留设备所属区域的均衡性指标。
在最小化参与任务的设备数量的过程中,参与任务的设备数量的生成算法伪代码如下(SE是指参与测控任务的设备集合,NE是指集合SE中设备的数量):

在最大化预留设备的重要性指标的过程中,定义航天测控设备集SD中的第j个设备Dj的重要性指标为Pj。其中,航天测控设备管理方给定航天测控设备集SD后,所有设备的重要性指标的总值就是一个常量,表示为因此,设备集合中参与任务的设备的重要性指标的总值如式(14)所示,则未参与任务的预留设备的重要性指标的总值表示为(P-PU)。所以,最大化预留设备的重要性指标就等同于需要最小化参与任务的设备的重要性指标。

式中:PU表示参与任务的设备集合SE中所有设备的重要性指标的总值。
在最大化预留设备所属区域的均衡性指标的过程中,定义航天测控设备集中的第j个设备Dj所属的区域为Qj,取值为国内的四大测控区域,即1表示西部区域,2表示东部区域,3表示南部区域,4表示北部区域。航天测控设备管理方给定航天测控设备集后,该集合中未参与任务的预留设备在四大测控区域中的个数则表示为Nt,其中t=1,2,3,4,分别表示在西部区域、东部区域、南部区域和北部区域中预留设备的个数。因此,预留设备所属区域的均衡性指标可以用各大区域中预留设备个数的标准差来进行衡量。标准差的取值越小,说明预留设备在四大测控区域中的分布越均衡。
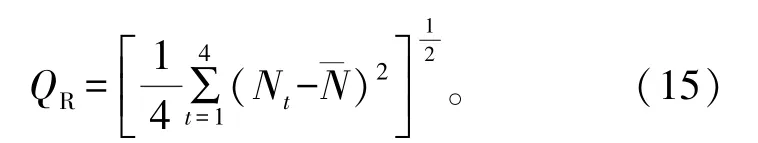
综上所述,航天测控资源优化配置问题采用的是两层优化目标,但本文重点研究在原子型任务满足率达到100% 的前提下,如何最大程度地提高设备利用率,也就是重点对第二层目标进行优化,进而给一些关键测控任务在四大测控区域中更加均衡地预留出更多、更重要的设备。因此,本文将航天测控资源配置优化模型中的目标函数定义为
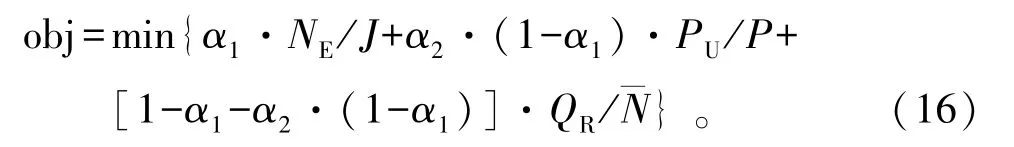
通过式(16)可以看出,目标函数是由3个乘积项(分别对应于上述的3个分目标)的加和构成,每个乘积项都对应于相应的参考值作了归一化处理,保证每个乘积项的数量级大小相同。权重系数α1和α2表示这3个分目标在目标函数中的权重不同,但又通过式(16)巧妙的构造形式保证了这3个分目标在目标函数中的权重之和为1,这也表明目标函数的取值范围为[0,1]。同时也可以看出,当权重系数α1=1时,目标函数就只考虑最小化参与任务的设备数量,也就相当于只考虑最大化预留设备的数量;当权重系数α1=0,α2=1时,目标函数就只考虑最小化参与任务的设备的重要性指标,也就相当于只考虑最大化预留设备的重要性指标;当权重系数α1=0,α2=0时,目标函数就只考虑最小化四大测控区域中预留设备个数的标准差,也就相当于只考虑最大化预留设备所属区域的均衡性指标。另外,当权重系数α1和α2取其他值时,目标函数就需要同时考虑以上3个分目标,使得到的航天测控资源优化配置方案能在国内四大测控区域中更加均衡地预留出更多、更重要的设备。
3 航天测控资源配置优化算法
3.1 航天测控资源配置优化问题求解框架
设计了如图3所示的航天测控资源配置优化问题的求解框架,统一了航天测控资源配置优化问题的求解算法的输入,将整个求解过程划分为输入数据预处理阶段和优化算法求解阶段这两个阶段,进而实现了航天测控资源配置需求与求解算法的解耦。其中,在输入数据预处理阶段,化解原子型任务之间非关联约束的关键步骤就是依据不同航天测控设备对不同航天器的支持能力的差异性,从所有星地可见预报中筛选出每个航天器完全可用的星地可见预报,从而形成每个原子型任务的备选可用弧段集;处理原子型任务之间关联约束的关键步骤就是依据原子型任务的备选可用弧段之间相互制约或冲突关系,生成每个原子型任务的每个备选可用弧段的冲突弧段集,这就相当于在求解阶段中优化算法给所有原子型任务调度一个相互之间不违反关联约束的可用弧段时,提前进行了冲突一致性检验的计算,大大减少了优化算法的运算时间。

图3 航天测控资源配置优化问题求解框架
3.2 可回溯的并行最佳优先搜索算法
3.2.1 算法总体描述
可回溯的并行最佳优先搜索的主要思想为:把原子型任务集合中的所有原子型任务都作为一个单独的节点,在每个节点的备选弧段集上使用多线程并行计算每个备选弧段的目标函数值,将其中的最小值作为该节点的目标函数值,与该最小目标函数值相对应的备选可用弧段作为该节点的当前候选弧段;在航天测控资源配置优化目标的指引下,选择能使总的优化目标函数值最小的节点作为当前候选节点,并利用当前候选节点的当前候选弧段的冲突集对剩下未选节点的备选弧段集进行剪枝,去除与当前候选弧段相冲突的所有备选弧段;周而复始直至所有节点都被选定了一个备选可用弧段,从而生成一棵记录了优化解构造路径的倒立多叉树。
如图4所示,在优化解的逐步构造过程中,依次选定了节点2、节点3和节点5作为每一步中的候选节点;当节点5作为当前候选节点时,如果在剩余未选的节点中出现备选弧段集被该节点的当前候选弧段剪枝为空的情况,就意味着在剩余未选的节点中出现了无备选可用弧段的原子型任务,此时可选择进行回溯操作,更替当前的候选节点或当前候选节点的当前候选弧段,使备选弧段集被剪枝为空的原子型任务恢复全部或部分备选可用弧段,从而保证原子型任务的满足率尽可能大。

图4 可回溯的并行最佳优先搜索示意图
3.2.2 回溯策略
为了使任务满足率达到100%,在航天测控资源配置优化解的构造过程中,可能会进行回溯操作。根据回溯操作的计算复杂程度,本文由简单到复杂设计了两种回溯策略。
(1)不更替当前候选节点的回溯策略
这种回溯策略的原则是不增加算法运算的开销,不去重新计算所有未选节点的目标函数值来更替当前候选节点。采用这种回溯策略时,只需要在当前候选节点的备选弧段集合中按照备选可用弧段的目标函数值从小到大依次更替当前候选弧段,直到剩余未选的节点中没有出现备选弧段集被该当前候选弧段剪枝为空的情况为止;如果当前候选节点的所有备选弧段均被更替完毕,在剩余未选的节点中仍然出现备选弧段集被剪枝为空的情况,则本策略认为参与航天测控资源配置优化的资源不足,确实不能支持任务满足率达到100%,其中一种处理方式为结束本次回溯操作,另外一种处理方式也可以是转为第二种回溯策略继续进行回溯。
(2)更替当前候选节点的回溯策略
这种回溯策略的原则是不考虑算法运算的开销,需要重新计算所有未选节点的目标函数值来更替当前候选节点。采用这种回溯策略时,需要将当前候选节点的当前候选弧段剔除后,再将当前候选节点置为未选节点,与其他未选节点一同计算目标函数值来重新选出当前候选节点,直到剩余未选的节点中没有出现备选弧段集被当前候选节点的当前候选弧段剪枝为空的情况为止;如果所有的当前候选节点均被更替完毕,在剩余未选的节点中仍然出现备选弧段集被剪枝为空的情况,则本策略同样认为参与航天测控资源配置优化的资源不足,确实不能支持任务满足率达到100%,应该结束本次回溯操作。
3.2.3 可回溯的并行最佳优先搜索算法
可回溯的并行最佳优先搜索算法流程如图5所示。

图5 可回溯的并行最佳优先搜索算法流程图
算法具体步骤如下:
Step1如果原子型任务集为空则失败退出,否则转Step 2。
Step 2把原子型任务集合中所有任务作为一个个单独的节点s放入未扩展节点表OPEN中,在每个原子型任务的备选弧段集上,计算每个备选弧段的目标函数,将其中的最小值作为当前节点的目标函数g(s),整个过程可通过并行计算得到;并按照g(s)对所有节点从小到大排序,初始化总的优化目标函数f=obj=0。
Step 3在具有相等的最小g(i)值的节点所构成的集合中,选择备选弧段数量最少的节点i进行扩展,并将其从OPEN表移至已扩展节点表CLOSED中,总优化目标函数更新为f=f+g(i)。
Step 4根据节点i已选弧段的冲突弧段集,在OPEN表中对剩下节点的备选弧段集进行剪枝,去除与已选弧段相冲突的备选弧段,以进一步减小搜索空间。
Step 5如果在剩余节点中出现备选弧段集被剪枝为空的情况,则转Step 7进行回溯,否则转Step 6。
Step6继续扩展节点i,多线程并行计算剩下的节点j的目标函数g(j),利用g(j)对OPEN表中剩下的节点重新排序,并转Step 10。
Step7根据当前采用的回溯策略,判断参与航天测控资源配置优化的资源是否确实不足,如果确实不足则转Step 8,否则转Step 9。
Step8当前采用的回溯策略认为参与航天测控资源配置优化的资源确实不能支持任务满足率达到100%,立即结束本次回溯操作,并将无备选可用弧段的节点从OPEN表移至未完成节点表INCOMPLETE中,并转Step 6。
Step9回溯节点i,采用3.2.2节中描述的回溯策略进行回溯操作,并更新总的优化目标函数值f,并转Step 4。
Step 10如果未扩展节点表OPEN为空,当前的已扩展节点表CLOSED就是航天测控资源配置优化方案,并根据输入的地面测控设备集SD和当前参与测控任务的设备集SE生成地面测控设备预留方案,算法结束,否则转Step 3。
4 仿真算例
4.1 仿真算例配置
航天器低轨任务需求如表2所示,航天测控设备如表3所示。

表2 地面测控资源配置需求描述
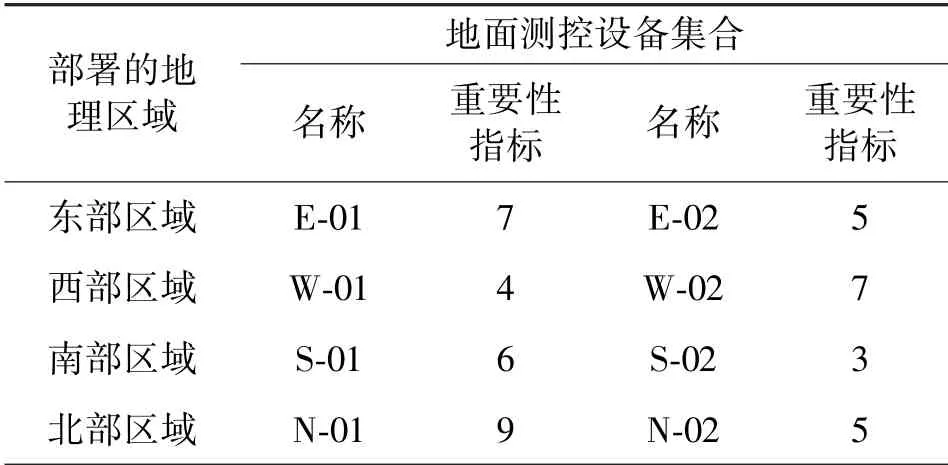
表3 航天测控设备描述
4.2 航天测控资源配置优化方案
4.2.1 航天测控资源调度方案
在一个主频为3.40 GHz、内存为8.00 GB的台式计算机上对本文提出的用于资源动态预留的航天测控资源配置优化算法进行仿真测试。在4.1节的仿真算例中,对优化目标计算公式(16)中的权重系数α1和α2均以0.01为步长在0~1范围内进行网格化搜索,经过多次试验发现,当权重系数α1取值在0.9附近和α2取值在0.4附近时,本文提出的算法运行得到的地面测控设备预留方案的优化效果较好,此时,得到的航天测控资源调度方案称为本文方案,具体数据可扫描本文OSID码查看。
同样对4.1节中配置的仿真算例进行优化计算,文献[12]提出的地基测控网资源分配算法运行得到的航天测控资源调度方案称为文献[12]方案,具体数据可扫描本文OSID码查看。
根据本文方案和文献[12]方案数据可知,两种算法运行得到的航天测控资源调度方案中设备执行任务的甘特图如图6所示。
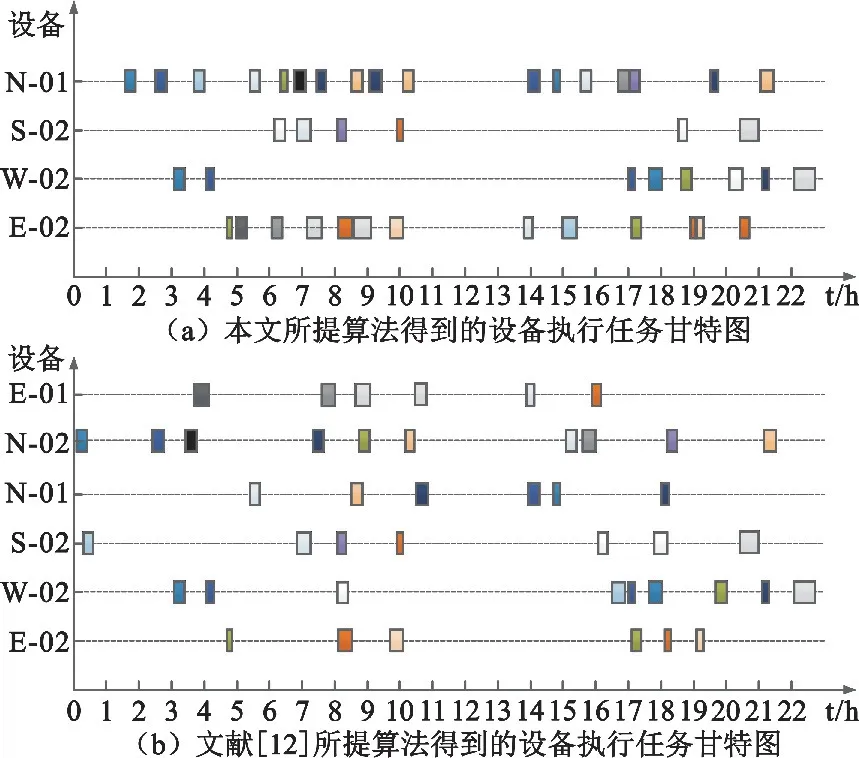
图6 两种算法得到的航天测控资源调度方案中设备执行任务的甘特图
4.2.2 地面测控设备预留方案
本文提出的算法运行得到的地面测控设备预留方案如表4所示。

表4 本文算法运行得到的地面测控设备预留方案
文献[12]提出的算法运行得到的地面测控设备预留方案如表5所示。

表5 文献[12]算法运行得到的地面测控设备预留方案
从表4和表5的对比可以看出,相比文献[12]提出的测控资源分配算法,本文提出的用于资源动态预留的航天测控资源配置优化算法能够预留出更多完全不参与测控任务的、且更重要的设备。此外,从图6的两种算法得到的航天测控资源调度方案中设备执行任务的甘特图也可以看出,本文所提算法能为参与测控任务的设备制定更加紧凑的工作计划,使得设备的资源利用率得到足够提升,进而在四大测控区域中能够更加均衡地预留出更多、更重要的设备。
5 结 论
本文从地面测控设备管理方的角度出发,建立了能在国内东部、西部、南部和北部四大测控区域中更加均衡地预留出更多、更重要的设备的航天测控资源配置优化模型,并提出了可回溯的并行最佳优先搜索算法对航天测控资源配置优化问题进行仿真求解。仿真结果表明,本文提出的航天测控资源配置优化算法能有效实现资源动态预留的预期效果。

