研储蓄之方 明消费之度

【摘 要】本文根据学生熟悉的消费与储蓄问题创建学习内容，通过Python的for循环编程来研究各储蓄方法的差异，进而教育学生储蓄有方、消费有度，不可盲目消费。

【关键词】for循环;储蓄;消费;案例

【中图分类号】G434 【文献标识码】A

【论文编号】1671-7384（2022）08-057-03

教学背景

本节课是教育科学出版社（2019）高中信息技术必修1《数据与计算》第2单元第3节“周而复始的循环”的第一节课“for循环的应用”。学习目标是了解循环的基本结构、学会计数循环的使用方法、熟练使用循环结构解决生活问题。本节知识相对简单易学，教学的关键在于如何将for循环融入具体问题解决中，教会学生学以致用。

大中小学生盲目消费后果严重并时常见诸媒体，这种现象不容忽视。究其原因是学生缺乏资金规划和理性消费的意识和能力，能否通过数据计算帮助学生加深认识并做到理性消费呢？笔者重构教材内容，设计了“研储蓄之方，明消费之度”一课，内容有趣又有益，还通过储蓄方案的计算与辨析引导学生进行高阶思维学习活动。

教学策略

本文从课程标准的要求出发，结合学生已有的理财经验和将来要经历的社会生活，以学生熟悉的消费与储蓄问题创建学习内容，设计与for循环结构学习相关的不同群体的个性消费需求。设置两条教学主线，明线为储蓄方案的选择与修正（生活教育、思政教育），渗透量入为出的消费观、未雨绸缪的储蓄观和生活问题的数字化解决意识;暗线是Python for循环知识的学习与应用（信息技术教育），学生需掌握循环结构相关知识与技能，并学会编程解决储蓄问题。

案例呈现

1.探究主题：一天一天积攒是我的小满足

教师以“一天一天积攒是我的小满足”引入储蓄话题，激发学生的兴趣，设计从中学生、大学生、刚参加工作的大学毕业生到新婚夫妻的个性消费需求与储蓄计划，要求学生通过编程计算选择合理的储蓄方案，具体问题如下。

①一个爱打篮球的中学生想省下零花钱买一双球鞋。

②一个大学生想从伙食费中节省出买笔记本电脑的钱。

③一个大学毕业刚参加工作、月收入5000元、每月房租1000元的摄影爱好者梦想拥有一部航拍无人机。

④一对平均月收入15000元的新婚夫妻想要存钱买车代步。

他们都想用一年的时间来存钱满足自己的愿望，你们会怎么建议呢？

上述4个问题具有挑战性：一是没有具体的钱数，需要学生根据生活经验、查阅资料或现场咨询进行商品的价值预估;二是题目提供的收入支出数据具有一定的迷惑性，潜在的必要消费（如衣、食、住、行）没有体现，考验学生的生活观察和经验积累。

2.储蓄方案：与编程计算巧结合

储蓄方案设计用心巧妙，有“365日存钱法”“月份倒数法”“52周存钱法”和“12月存单法”。在方案设计过程中充分考虑学生学情差异，知识难度分层，方法上一题多解，满足分层教学需求。

（1）12月存单法

难度值：*

方案描述：每月存100元，存12个月。

设计意图：每月定存100元，存钱方法简单。在程序设计上，循环初值、终值、步长、循环体都直观明确，学生能轻松编写程序求解问题。

程序实现：

smoney=0

for month in range（12）： # range（12）也可写成range（1，13）

smoney=smoney+100

print（smoney）

（2）365日存钱法

难度值：*

方案描述：设计并打印一张填好1～365数字的表格。每天存一次钱，钱数在1～365之间且不重复，存好后在对应表格的数字上涂上标记，坚持储蓄一年。

设计意图：每天存入钱数的不确定性似乎让问题变得没有规律可循，但以一年的时间长度来看，本题的意思就是将代表1～365数字的格子填满。

程序实现：

smoney= 0

for day_money in range（1，366）：

smoney = smoney + day_money

print（smoney）

（3）52周存钱法

难度值：**

方案描述：一年有52周，故称52周存钱法。第一周存10元，第二周存20元，每周递增10元。

设计意图：学生必需明确三个变化的量（周数week，每周存入的钱数week_money，总钱数smoney）。预测大部分学生会想到week_money=week_money+10的解决方法，少部分思维活跃的学生会发现week_money与week之间的联系，利用smoney=smoney+week*10简化程序。极少数优秀学生可能会直接以week_money作为循环控制变量，利用smoney=smoney+week_money来解决问题。在问题设计中加入可能性预设，鼓励学生发散思维，巧解问题。

程序实现：

smoney= 0

week_money=0

for week in range（52）：

week_money= week_money+10

smoney=smoney+ week_money

print（smoney）

（4）月份倒数法

难度值：***

方案描述：假设平均每个月有30天 ，第一天存入30元，第二天存29元，第三天存28元，依次递减，直到第30天存入1元，完成一个月的存钱计划。每个月都照此方法存钱，存够一年。

设计意图：这个题目的难度有两方面：一是递减式循环，二是要将求一年的存钱数转化为先求一个月的存钱数，再计算一年的总存钱数。在递减式循环中学生要理解初值、终值及步长的意义并设定好。

程序实现：

smoney= 0

for day_money in range（30，0，-1）：

smoney=smoney+ day_money

smoney= smoney*12

print（smoney）

3.分组合作，编程求解

教师通过案例简单讲解for循环结构的语法和应用方法，提供导学案及相关的微课视频。采取“小组合作，分析储蓄方案→分工编写程序→测试验证→根据计算结果讨论并完成消费需求—储蓄方案连线图”的分组合作学习方式，让学生体验“合→分→合”的深度分工合作学习方式。

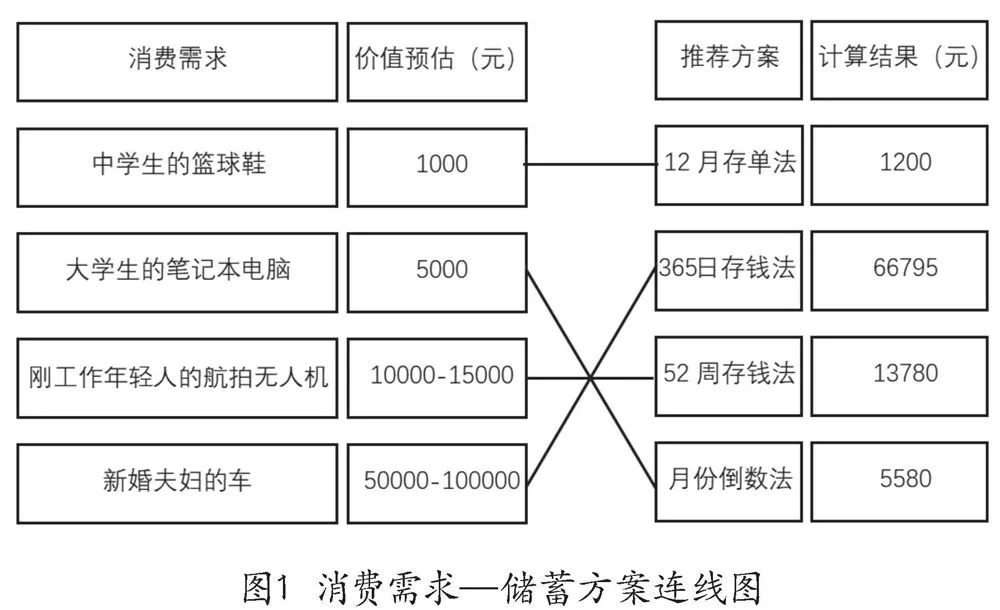
储蓄方案中有意不提供测试数据，在测试验证环节中，学生可与数学计算相印证或与同写一个程序的学生相互验证，并将结果填入导学案中“消费需求—储蓄方案连线图”（图1）中的“计算结果”栏中。

在讨论环节中，学生需讨论并预估每种商品大约需要花费的金额并填入对应的“价值预估”一栏中，并将“消费需求”与“推荐方案”进行连线匹配，最终得到大致如图1的结果。

4.方案讨论，激发创意

方案讨论环节包含网络学习平台上的“小组学习成果评价”和“班级内现场发言讨论”两个环节。

环节1：各小组在OJ平台对其他小组的完成效果进行评价。评价内容包括：①4个编程题目的完成情况;②代码的科学性、简洁性、创新性;③图1连线的正确性，根据导学案提供的评价标准进行评分并作简要评价。

环节2：班级内现场发言讨论，讨论方案的合理性以及如何改进才能更具创新性、科学性、实用性。学生的想象力和创造力远超笔者预估，足见还课堂于学生的效果。

思考：365日存钱法。这种方法不好进行具体操作，存入的金额差距太大，强制按图执行，会不会很麻烦？

改进：月份倒数法。存钱日期建议改为从发工资之日开始，存钱的数目多少与收入支出的剩余相对应，减少存钱的压力。

争论：52周存钱法。在这个存钱法的讨论中，有两种声音：一是每周的压力递增，很不合理;二是当节约和储蓄变成一种习惯后，虽然压力越来越大，但看着钱数的递增，动力也越来越大，反而乐在其中，不觉得是一种负担。

共识：选择哪种存钱方法看个人喜好，明确自己必要的消费项目、消费金额，权衡收入水平、储蓄时长、储蓄方法，做到有计划、有规划并持之以恒才是最重要的，避免盲目消费和成为月光族。

亮点：有的学生提到为什么不存入银行或余额宝呢？这样还有利息收入;有的提出如果钱不够的话可以借钱购买或贷款消费再慢慢还。这些都是很有现实意义并值得探究的观点，可作为后续研究。

5.总结升华：储蓄建议，理性消费

通过上述几个步骤的学习思考，学生一步步明确储蓄的意义，理解存钱不等于抠门儿;普遍认同坚持每日记账，了解资金去向，拒绝诱惑与冲动消费的观点;还提议如果没有很强的克制力，最好不用信用卡、不网络贷款。

6.课后作业：方案创设，延伸探究

围绕课堂提及的利息，引导学生进行方案创设的课后实践活动。以小组为单位，计算10000元存入银行、余额宝等1年后的利息收入，并将计算过程与结果、推荐的储蓄方案发布到班级交流平台。

创新性

1.多样化与创新性

本案例中多样化的消费问题、储蓄方案、编程思路的设计，有助于培养学生的发散思维，激发创意。

2.争议与共识

受个人消费水平和认知差异的影响，学生对各消费项目价值评估存在较大争议，通过计算又最终达成共识，这有助于培养学生用数据说话的科学精神和求同存异的包容思想。

3.延伸思考

考虑到理财话题的受欢迎程度，还可将银行储蓄、高消费、高利贷、非法集资等形成大项目进行教学，让学生明确如何理性消费与投资，避免误入理财陷阱，防范金融诈骗。

结 语

本节课及课后活动不仅让学生感受到了循环结构编程计算的魅力，还引导学生利用编程计算明确收入与支出、储蓄与消费的关系，树立正确的储蓄观和消费观。这是信息技术学科知识讲授与学生核心素养培养相融合的体现，是思政教育与学科教育融合的体现，是培养用数据说话的科学意识，是运用信息技术解决生活问题的典型实例，也是引导学生更好地树立正确的消费观、落实立德树人教育的有效途径。

注：本文系福建省教育科学“十三五”规划2020年度立项课题“基于网络公共事件的高中生信息社会责任教育实践研究”（课题编号：2020XB1299）的研究成果之一

作者单位：福建南安第一中学